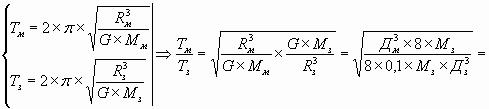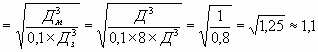в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 416 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Рассмотрите таблицу, содержащую сведения о ярких звёздах.
| Наименование звезды | Температура поверхности, K |
Масса (в массах Солнца) |
Радиус (в радиусах Солнце) |
Средняя плотность по отношению к плотности воды |
|---|---|---|---|---|
| Альдебаран | 3600 | 5,0 | 45,0 | |
| 11 000 | 10,2 | 3,5 | 0,33 | |
| Ригель | 11 200 | 40,0 | 138,0 | |
| Сириус A | 9250 | 2,1 | 2,0 | 0,36 |
| Сириус B | 8200 | 1,0 | 0,01 | |
| Солнце | 6000 | 1,0 | 1,0 | 1,4 |
| 5730 | 1,02 | 1,2 | 0,80 |
Выберите все верные утверждения, которые соответствуют характеристикам звёзд.
1) Температура звезды Центавра А соответствует температуре звёзд спектрального класса О.
2) Звезда Ригель является сверхгигантом.
3) Наше Солнце относится к гигантам спектрального класса B.
4) Средняя плотность звезды Сириус В больше, чем у Солнца.
5) Звезда ε Возничего В относится к звёздам главной последовательности на диаграмме Герцшпрунга-Рессела.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Задания Д29 C2 № 4439
Известно, что один оборот вокруг своей оси Венера совершает примерно за 243 земных суток, а масса Венеры составляет 0,82 от массы Земли. На орбиту какого радиуса надо вывести спутник Венеры, чтобы он всё время «висел» над одной и той же точкой поверхности? Известно, что спутники Земли, «висящие» над одной и той же точкой поверхности, летают по орбите радиусом км.
Рассмотрите таблицу, содержащую сведения о ярких звездах.
| Наименование звезды | Температура, К | Масса (в массах Солнца) | Радиус (в радиусах Солнца) | Расстояние до звезды (св. год) |
|---|---|---|---|---|
| Альдебаран | 3500 | 2,5 | 43 | 65 |
| Альтаир | 8000 | 1,7 | 1,7 | 17 |
| Бетельгейзе | 3600 | 15 | 1000 | 650 |
| Вега | 9600 | 2 | 3 | 25 |
| Капелла | 5000 | 3 | 12 | 42 |
| Кастор | 10400 | 2 | 2,5 | 50 |
| Процион | 6600 | 1,5 | 2 | 11 |
| Спика | 22000 | 11 | 8 | 260 |
Выберите два утверждения, которые соответствуют характеристикам звезд, и укажите их номера.
1) Температура поверхности и радиус Бетельгейзе говорят о том, что эта звезда относится к красным сверхгигантам.
2) Температура на поверхности Проциона в 2 раза ниже, чем на поверхности Солнца.
3) Звезды Кастор и Капелла находятся на примерно одинаковом расстоянии от Земли и, следовательно, относятся к одному созвездию.
4) Звезда Вега относится к белым звездам спектрального класса А.
5) Так как массы звезд Вега и Капелла одинаковы, то они относятся к одному и тому же спектральному классу.
Источник: Демонстрационная версия ЕГЭ—2018 по физике
Рассмотрите таблицу, содержащую сведения о ярких звёздах.
| Наименование
звезды |
Температура
поверхности, К |
Масса
(в массах Солнца) |
Радиус
(в радиусах Солнца) |
Плотность по
отношению к плотности воды |
|---|---|---|---|---|
| Альдебаран | 3600 | 5,0 | 45 | 77,7 · 10–5 |
| α Центавра А | 5730 | 1,02 | 1,2 | 0,80 |
| ε Возничего В | 11000 | 10,2 | 3,5 | 0,33 |
| Солнце | 6000 | 1,0 | 1,0 | 1,4 |
| Сириус В | 8200 | 1 | 2 · 10–2 | 1,75 · 106 |
| Сириус А | 9250 | 2,1 | 2,0 | 0,36 |
| Капелла | 5200 | 3,3 | 23 | 4 · 10–4 |
| Ригель | 11 200 | 40 | 138 | 2 · 10–5 |
Выберите два утверждения, которые соответствуют характеристикам звёзд.
1) Звезда Сириус А относится к звёздам главной последовательности на диаграмме Герцшпрунга — Рассела.
2) Звезда Ригель относится к сверхгигантам.
3) Наше Солнце имеет максимальную массу для звёзд главной последовательности на диаграмме Герцшпрунга — Рассела.
4) Звезда Сириус В относится к звёздам главной последовательности на диаграмме Герцшпрунга — Рассела.
5) Звезда Центавра А относится к белым карликам.
Источник: ЕГЭ по физике. Вариант 114
На рисунке представлена диаграмма Герцшпрунга−Рессела.
Выберите все верные утверждения о звёздах.
1) Плотность белых карликов существенно больше средней плотности звёзд главной последовательности.
2) «Жизненный цикл» звезды спектрального класса О главной последовательности более длительный, чем звезды спектрального класса М главной последовательности.
3) Температура поверхности звёзд спектрального класса G выше температуры поверхности звёзд спектрального класса O.
4) Звезда Бетельгейзе относится к голубым звёздам главной последовательности, поскольку её радиус почти в 1000 раз превышает радиус Солнца.
5) Звезда Альтаир, имеющая радиус 1,9RO, относится к звёздам главной последовательности.
Источник: Демонстрационная версия ЕГЭ—2021 по физике
Искусственный спутник движется вокруг Земли, всё время находясь на расстоянии R от её центра (R заметно превышает радиус Земли). Установите соответствие между зависимостями, описывающими движение спутника по орбите (см. левый столбец), и выражающими эти зависимости уравнениями, приведёнными в правом столбце (константа A выражена в соответствующих единицах без кратных и дольных множителей).
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ
А) Зависимость модуля ускорения спутника от радиуса его орбиты
Б) Зависимость угловой скорости спутника от радиуса его орбиты
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) где A — некоторая постоянная величина
2) где B — некоторая постоянная величина
3) где С — некоторая постоянная величина
4) где D — некоторая постоянная величина
В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли увеличивается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус орбиты | Скорость движения
по орбите |
Период обращения
вокруг Земли |
Спутник Земли перешел с одной круговой орбиты на другую с меньшим радиусом орбиты. Как изменились в результате этого перехода центростремительное ускорение спутника, скорость его движения по орбите и период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Центростремительное
ускорение |
Скорость движения
по орбите |
Период обращения
вокруг Земли |
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменятся радиус траектории, период обращения и кинетическая энергия частицы при увеличении скорости её движения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус
траектории |
Период
обращения |
Кинетическая
энергия |
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменится радиус траектории, период обращения и кинетическая энергия частицы при уменьшении скорости ее движения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус
траектории |
Период
обращения |
Кинетическая
энергия |
В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась,
2) уменьшилась,
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус орбиты | Скорость движения
по орбите |
Период обращения
вокруг Земли |
В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличивается. Как изменяются в результате этого перехода радиус орбиты спутника, его центростремительное ускорение и период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус орбиты | Центростремительное
ускорение |
Период обращения
вокруг Земли |
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью –частица, радиус окружности, частота обращения и энергия
–частицы по сравнению с протоном должны:
1) увеличиться
2) уменьшиться
3) не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус окружности | Частота обращения | Энергия частицы |
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 2., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 4.
Задания Д2 B2 № 5285
Точка движется по окружности радиусом R с частотой обращения Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
1) увеличить в 4 раза
2) уменьшить в 4 раза
3) уменьшить в 2 раза
4) увеличить в 2 раза
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 6.
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, центростремительное ускорение и период обращения α-частицы по сравнению с протоном должны:
1) увеличиться
2) уменьшиться
3) не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус окружности | Центростремительное
ускорение |
Период обращения |
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 6.
Космический зонд стартовал с Земли и через некоторое время опустился на другую планету, масса которой больше массы Земли в 8 раз, а радиус больше радиуса Земли в 2 раза. Определите, как в результате этого космического перелёта изменятся следующие физические величины, измеряемые зондом, по сравнению со значениями для Земли: ускорение свободного падения на поверхности планеты, первая космическая скорость для планеты. Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Ускорение свободного падения на
поверхности планеты |
Первая космическая скорость
для планеты |
Космический зонд стартовал с Земли и через некоторое время опустился на другую планету, масса которой меньше массы Земли в 4 раза, а радиус больше радиуса Земли в 2 раза.
Определите, как в результате этого космического перелёта изменятся следующие физические величины, измеряемые зондом, по сравнению со значениями для Земли: ускорение свободного падения на поверхности планеты, первая космическая скорость для планеты. Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Ускорение свободного падения на
поверхности планеты |
Первая космическая скорость
для планеты |
Аквариум имеет прозрачные вертикальные стенки: три плоские (боковые и заднюю) и одну цилиндрическую (переднюю), с радиусом R = 0,8 м. В него налита вода с показателем преломления n = 4/3. Мальчик, глядя на маленькую рыбку в аквариуме по горизонтали, перпендикулярно цилиндрической стенке, видит рыбку (точнее, её изображение) на расстоянии b = 16 см от этой стенки (см. рис.). На каком расстоянии a от этой стенки будет видна рыбка, если мальчик будет смотреть на неё сквозь поверхность воды по вертикали, сверху вниз?
Аквариум имеет прозрачные вертикальные стенки: три плоские (боковые и заднюю) и одну цилиндрическую (переднюю), с радиусом R = 0,8 м. В него налита вода с показателем преломления n = 4/3. Мальчик, глядя в аквариум сверху (см. рис.), видит маленькую рыбку в аквариуме на расстоянии a = 20 см от его передней стенки. На каком расстоянии b от этой стенки будет видна рыбка, если мальчик будет смотреть на неё по горизонтали, перпендикулярно стенке?
Точечный источник света находится в ёмкости с жидкостью и опускается вертикально вниз от поверхности жидкости. При этом на поверхности жидкости возникает пятно, в пределах которого лучи света от источника выходят из жидкости в воздух. Глубина погружения источника (расстояние от поверхности жидкости до источника света), измеренная через равные промежутки времени, а также соответствующий радиус светлого пятна представлены в таблице. Погрешность измерения глубины погружения и радиуса пятна составила 1 см. Выберите все верные утверждения на основании данных, приведённых в таблице.
| Глубина погружения, см | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Радиус пятна, см | 12 | 24 | 36 | 48 | 60 | 72 | 84 |
1) Образование упомянутого пятна на поверхности обусловлено дисперсией света в жидкости.
2) Предельный угол полного внутреннего отражения меньше 45°.
3) Показатель преломления жидкости меньше 1,5.
4) Образование пятна на поверхности обусловлено явлением полного внутреннего отражения.
5) Граница пятна движется с ускорением.
Источник: Демонстрационная версия ЕГЭ−2017 по физике
Всего: 416 1–20 | 21–40 | 41–60 | 61–80 …
Искусственный спутник планеты — это
тело, которое обращается вокруг планеты.
Движение спутников происходит по эллипсам, но
при решении заданий ЕГЭ, траекторией движения
считают упрощенный частный случай — движение по
окружности.
В основу расчетов положены следующие законы и
формулы:
1) Закон всемирного тяготения (з.в.т.)
— з.в.т.,
где: — гравитационная
постоянная;
— масса
планеты
— масса
спутника
— орбита, по
которой движется спутник
— орбита
— радиус
планеты
— высота
спутника
2) Второй закон Ньютона (II з.Н)
— II з.Н., где:
— масса
спутника
— радиус
орбиты
— скорость
спутника
—
центростремительное ускорение
3) Сила тяжести
— сила
тяжести, где: —
масса спутника
— ускорение
свободного падения на высоте
(, если
у поверхности Земли)
4) Линейная скорость тела, движущегося по
окружности
— линейная
скорость, где:
— радиус
орбиты
— период
вращения
5) Импульс тела
— импульс
тела, где:
— масса
спутника
— скорость
спутника
6) Кинетическая энергия
—
кинетическая энергия, где:
— масса
спутника
— скорость
спутника
7) Масса планеты
— масса
планеты, где:
— плотность
— объем
планеты —
объем шара
— радиус
планеты (шара)
Примеры законов, формул:
Табличные данные:
Примеры решения заданий ЕГЭ (2008 г.)
Задача 1 (№25). Космонавт, находясь на Земле,
притягивается к ней с силой 700Н. С какой
приблизительно силой он будет притягиваться к
Марсу, находясь на его поверхности? Радиус Марса
в 2 раза, а масса — в 10 раз меньше, чем у Земли.
Ответ: 4
Задача 2 (№26). Космический корабль движется
вокруг Земли по круговой орбите радиусом . Его скорость
равна
Ответ: 1
Задача 3 (№27). Космическая ракета удаляется от
Земли. На каком расстоянии от земной поверхности
сила гравитационного притяжения ракеты Землей
уменьшится в 4 раза по сравнению с силой
притяжения на земной поверхности? (Расстояние
выражается в радиусах Земли R).
Ответ: 1
Задача 4 (№28). Во сколько раз сила притяжения
Земли к Солнцу больше силы притяжения Меркурия к
Солнцу? Масса Меркурия составляет массы Земли, а расположен
он в 2,5 раза ближе к Солнцу, чем Земля.
Ответ: 2
Задача 5 (№29). Средняя плотность планеты Плюк
равна средней плотности планеты Земля, а радиус
Плюка в два раза больше радиуса Земли. Во сколько
раз первая космическая скорость для Плюка
больше, чем для Земли?
Ответ: 2
Задача 6 (№30). Искусственный спутник
обращается по круговой орбите на высоте 600 км от
поверхности планеты. Радиус планеты равен , ускорение
свободного падения на поверхности планеты равно . Какова
скорость движения спутника по орбите?
Ответ: 1
Примеры решения заданий ЕГЭ (уровень С)
С1. Масса Марса составляет 0,1 от массы Земли,
диаметра Марса вдвое меньше, чем диаметр Земли.
Каково отношение периодов обращения
искусственных спутников Марса и Земли , движущихся по
круговым орбитам на небольшой высоте?
| Дано: | Решение: |
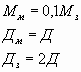 |
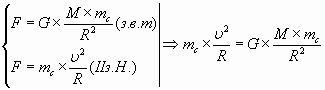
Период обращения спутника: (1)>(2): |
Ответ: 1,1
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.
Алгоритм решения задания 1:
- Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
- Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
- Выбирайте наиболее подходящую для решения формулу.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Уравнение движения тела имеет вид x = 2t + 0,5t2. Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с2).
Решение
Дано:
$x=2t+0.5t^2$
$a-?$
Решение:
Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.
Ответ: 1
Задача 2
Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).
Решение
Дано:
$υ_1=60$км/ч
$S_1={1}/{4}S$
$S_2={3S}/{4}$
$υ_{ср}=40$км/ч
$υ_2-?$
Решение:
Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).
Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.
Ответ: 36
Задача 3
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2
Решение
Дано:
$m=50$кг
$g=10м/с^2$
$l=5$м
$υ=6$м/c
$N-?$
Решение:
При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.
Ответ: 860
Задача 4
Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).
Решение
Дано:
$υ_1=3$м/с
$υ_2=4$м/с
$υ_{отн}-?$
Решение:
Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.
Ответ: 5
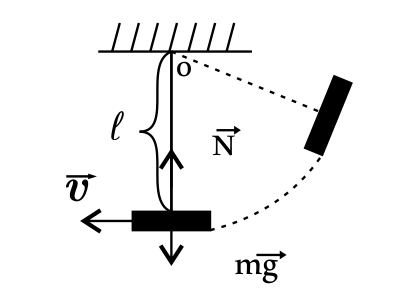
Задача 5
Автобус, масса которого 15 т, движется с ускорением 0,7 м/с2. Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).
Решение
Дано:
$m=15·10^3$кг
$a=0.7м/с^2$
$μ=0.03$
$F_{тяги}-?$
Решение:
На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).
В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.
Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.
Ответ: 15
Задача 6
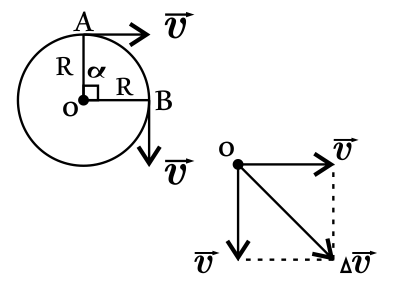
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14
Решение
Дано:
$R=1$м
$α=90°$
$T=3.14$c
$∆υ-?$
Решение:
Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).
Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).
Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.
Ответ: 2.8
Задача 7
Тело движется вдоль оси Ox. Чему равна проекция скорости тела vx, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).
Решение
Дано:
$x=3-2t$
$υ_х-?$
Решение:
Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.
Ответ: -2
Задача 8
Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$
Решение
Дано:
$υ=3$м/с
$t=4$c
$υ_к-?$
Решение:
На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$
$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.
Ответ: 37
Задача 9
Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t2, где все величины выражены в системе СИ? Ответ выразить в (м).
Решение
Дано:
$t=10$c
$x=3-2t+t^2$
$x_0=3$
$r-?$
Решение:
$x=-20+100=80+3=83$
$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.
Ответ: 80
Задача 10
Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 1024 кг. Ответ выразить в (·1024 кг).
Решение
Дано:
$R_n={R_3}/{2}$
$M_n-?$
$g_n=g_3$
$M_3=6·10^{24}$м
Решение:
${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг
Ответ: 1.5
Задача 11
Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).
Решение
Дано:
$R={1.5}{π}$
Решение:
Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.
Ответ: 0
Задача 12
Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 106 м. Ответ выразите в (км).
Решение
Дано:
$M_n={M_3}/{4}$
$R_n-?$
$g_n=g_3$
$R_3=6.4·10^6$м
Решение:
${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$
$R_n=3200$км
Ответ: 3200
Задача 13
Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с2).
Решение
Дано:
$g_n-?$
$T_n=1.41$с
$T_3=1c$
Решение:
${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$
$g_n=5м/с^2$
Ответ: 5
Задача 14
Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).
Решение
Дано:
$m=0.8$кг
$υ=5$м/с
$F_{тяж}-?$
Решение:
Модуль силы тяжести, равна: $m·g=0.8·10=8H$
Ответ: 8
Задача 15
Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с2). Ускорение свободного падения на Земле принять равным 10 м/с^2
Решение
Дано:
$R_n=R_3$
${ρ_3}/{2}=ρ_n$
$ρ_n-?$
Решение:
${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$
а $V={4}/{3}π·R^3$, то и $V_n=V_3$.
${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.
Ответ: 5
Задача 16
Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).
Решение
Дано:
$m_1=0.4$кг
$m_2=0.3$кг
$x_1=10^{-1}$ м=10 см
$x_2-?$
Решение:
${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$
Ответ: 7.5
Задача 17
Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).
Решение
Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.
Ответ: 6.4
Задача 18
Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).
Решение
Дано:
$А=2·H$
$∆x=4·10^{-2}$
$K-?$
Решение:
По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.
Ответ: 50
Задача 19
Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.
Решение
Дано:
${L}/{|S↖{→}|}-?$
$t={T}/{2}$
Решение:
1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$
3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$
Ответ: 1.57
Задача 20
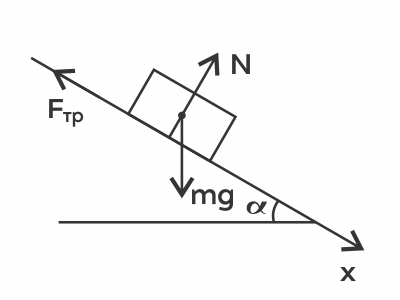
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.
Решение
Дано:
$m=2$кг
$α=30°$
$μ=0.7$
Найти:$F_{тр}-?$
Решение:
Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)
Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$
$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$
Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.
Ответ: 10
Рекомендуемые курсы подготовки
Элементы астрофизики. Солнечная система, звёзды, галактики
В. З. Шапиро
Задание 24 ЕГЭ по физике – это основы астрофизики. Здесь необходимо выбрать несколько утверждений из пяти предложенных.
Для этого необходимо изучить диаграмму Герцшпрунга – Рессела: величины, отложенные по осям, и закономерности, которые отражены на диаграмме. Кроме того, надо обратить внимание на различия в средней плотности звёзд главной последовательности (порядка плотности воды), белых карликов и гигантов.
На рисунке представлена диаграмма Герцшпрунга – Рессела
Выберите все верные утверждения о звёздах.
| 1) | Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, а значит, она относится к сверхгигантам. |
| 2) | Плотность белых карликов существенно больше средней плотности гигантов. |
| 3) | «Жизненный цикл» звезды спектрального класса K главной последовательности более длительный, чем звезды спектрального класса В главной последовательности. |
| 4) | Температура поверхности звёзд спектрального класса G выше температуры поверхности звёзд спектрального класса А. |
| 5) | Звезда Антарес имеет температуру поверхности 3300 К и относится к звёздам спектрального класса А. |
Ответ: ___________________________.
Необходимая теория:
По горизонтальной оси диаграммы Герцшпрунга-Рессела отложены спектральные классы в порядке понижения температур звезд, начиная со спектрального класса О (очень горячие звезды) слева и заканчивая спектральным классом М (относительно холодные звезды) справа.
По вертикальной оси отложены светимости или абсолютные звездные величины. Каждая звезда имеет какую-то определенную абсолютную величину и относится к какому-то определенному спектральному классу, а потому может быть представлена точкой в определенном месте диаграммы. В среднем, чем горячее звезда, тем она ярче. Поэтому, чем левее находился на диаграмме спектральный класс исследуемой звезды (и значит, чем больше ее температура), тем выше оказывалась она по шкале абсолютных величин. В результате большинство звезд, нанесенных на диаграмму, расположилось по диагонали от верхнею левого угла к нижнему правому. Они образуют так называемую главную последовательность. По современной оценке, более 90% всех доступных нашему наблюдению звезд попадают на главную последовательность. Диаграмма Герцшпрунга-Рессела даёт возможность найти абсолютную величину нужной звезды по её спектральному классу (особенно точно это работает для спектральных классов O—F), оценить её примерный возраст и представить ближайшее будущее и прошлое наблюдаемого объекта.
Проверим каждое из предложенных утверждений.
1. На главной последовательности располагаются звезды, радиусы которых сравнимы или немного превышают радиус Солнца. Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, поэтому, согласно диаграмме, она относится к сверхгигантам. Утверждение верное.
2. Массы белых карликов сравнимы с массой Солнца, а массы гигантов только в десятки раз превышают солнечную массу. По диаграмме видно, что белые карлики имеют диаметр порядка 0,01 солнечного, а гиганты — 10 солнечных. В соответствии с формулой плотности это утверждение верное.
3. Звезда спектрального класса K главной последовательности имеет сравнимую с солнечной светимость , а светимость звезды спектрального класса В главной последовательности в тысячи раз превышает солнечную. Значит, звезда спектрального класса K медленнее тратит свою внутреннюю энергию и имеет более длительный «жизненный цикл». Утверждение верное.
4. В соответствии с диаграммой спектральному класс G соответствует температура около 5500 К, а спектральному классу А – температура 9000 К. Поэтому это утверждение неверное.
5. Точно также, как и в предыдущем утверждении, по диаграмме можно определить спектральный класс для соответствующей температуры. Указанной температуре 3300 К соответствует спектральный класс М. Поэтому это утверждение неверное.
Ответ: 1, 2, 3.
Секрет решения. Данное задание надо выполнять в строгом соответствии с прилагаемой диаграммой Герцшпрунга-Рессела. Но иногда встречаются задачи, в которых сама диаграмма не представлена. Запомнить последовательность спектральных классов можно по фразе «Один бритый англичанин финики жевал, как морковь». Первой букве каждого слова соответствует наименование спектрального класса в порядке понижения температуры.
«Один(О) бритый (В) англичанин (А) финики(F) жевал(G) как(K) морковь(M)».
Есть и еще одна «запоминалка»:
O, Be A Fine Girl, Kiss Me!
- Рассмотрите таблицу, содержащую характеристики некоторых спутников планет Солнечной системы.
| Название спутника | Радиус спутника, км | Радиус орбиты, тыс. км | Вторая космическая скорость, м/с | Планета |
| Луна | 1737 | 384,4 | 2400 | Земля |
| Фобос | ~12 | 9,38 | 11 | Марс |
| Ио | 1821 | 421,6 | 2560 | Юпитер |
| Европа | 1561 | 670,9 | 2025 | Юпитер |
| Каллисто | 2410 | 1883 | 2445 | Юпитер |
| Титан | 2575 | 1221,8 | 2640 | Сатурн |
| Оберон | 761 | 583,5 | 725 | Уран |
| Тритон | 1354 | 354,8 | 1438 | Нептун |
Выберите все верные утверждения, которые соответствуют характеристикам спутников.
| 1) | Объём Оберона примерно в 2 раза меньше объёма Европы. |
| 2) | Первая космическая скорость для искусственного спутника Луны составляет примерно 1,7 км/с. |
| 3) | Чем больше радиус орбиты спутника, тем больше масса планеты, вокруг которой он вращается. |
| 4) | Объём Луны больше объёма Европы. |
| 5) | Ускорение свободного падения на Фобосе составляет примерно 11 м/с2. |
Ответ: ___________________________.
Необходимая теория. Сила тяготения
Проверим каждое из предложенных утверждений.
1. Объем спутника можно рассчитать, используя формулу объема шара.
Подставляя данные из таблицы, проведем расчет.
Такой подробный расчет можно было заменить следующими рассуждениями.
Так как радиусы спутников отличаются в 2 раза 
Утверждение неверное.
2. Первая и вторая космические скорости связаны соотношением:
Отсюда первая космическая скорость равна:
Проведем расчет.
Утверждение верное.
3. Юпитер, у которого самая большая масса из предложенных в таблице планет, имеет спутник Ио, находящийся на орбите радиусом 421,6 тыс. км, а у Урана спутник Оберон имеет орбиту 583,5 тыс. км. Масса Урана значительно меньше массы Юпитера, поэтому это утверждение неверное.
4. Для сравнения объемов Луны и Европы проведение расчетов не требуется. Достаточно увидеть, что радиус Луны больше радиуса Европы, поэтому объем Луны также будет больше. Утверждение верное.
5. Ускорение свободного падения можно рассчитать по формуле:
где
– первая космическая скорость, R – радиус спутника. Первую космическую скорость выразим через вторую
Проведем расчет
Утверждение неверное.
Ответ: 2, 4.
Секрет решения. Для решения подобных задач требуются прочные знания по темам «Закон всемирного тяготения», «Ускорение свободного падения», «Первая и вторая космические скорости». Кроме формул, надо уметь проводить «громоздкие» расчеты на калькуляторе и не забывать про перевод единиц измерения в систему СИ.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 24 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023