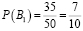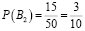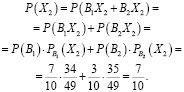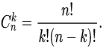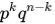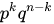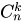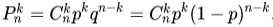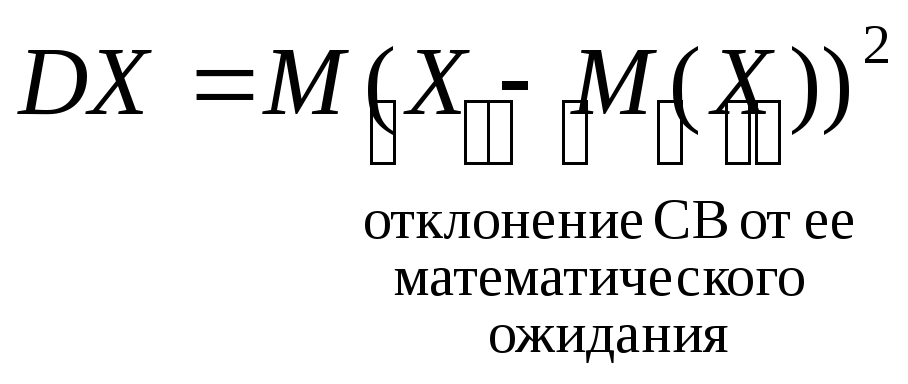ВЕРОЯТНОСТЬ УСПЕШНОЙ СДАЧИ ЭКЗАМЕНА
Эта задача встает практически перед каждым студентом по крайней мере дважды в год. Мало кто выучивает все экзаменационные вопросы. И часто бывает, что хочется узнать свои шансы, достаточно ли уже выучил, чтобы почти наверняка получить четверку? Конечно, учить надо все вопросы, предмет нужно знать. Но обстоятельства бывают разные… Итак!
Перед экзаменом Вы получили список из N вопросов. Известно, что в билете будет содержаться B вопросов, но распределение их по билетам заранее неизвестно. К экзамену Вы успели выучить только M вопросов. Какова вероятность P того, что во взятом Вами билете Вы будете знать T вопросов? (Все числа должны быть реальные и осмысленные!)
Введите общее число вопросов N:
Введите число выученных вопросов M:
Введите число вопросов в билете B:
Для получения результата нажмите кнопку
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Ревегук Ю.А.
1
Рудикова Е.С.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
Вокруг нас происходит так много вещей и событий, которые, несмотря на уровень развития науки, трудно спрогнозировать. Сложно предугадать с каким номером выпадет бочонок при игре в лото или сколько будет солнечных дней в году. Но при этом, имея дополнительные сведения, возможно прогнозировать и вычислять вероятность таких событий. В данной статье идет речь о теории вероятности, составлен алгоритм решения задач по этой теме, а так же приведены примеры, с помощью которых возможно вычислить вероятность выпадения «счастливого» билета на экзамене. Теория вероятности – это отличный помощник, при предсказании наступления определенного события, в том числе выпадения «счастливого» билета на экзамене. Простые формулы позволяют провести расчеты любому человеку.
теория вероятности
«счастливый» билет
задачи
1. Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция / Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев, 2011. – С. 124–127.
2. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика: рабочая тетрадь. – Ставрополь, 2015.
3. Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере // Вестник АПК Ставрополья. – 2017. – № 2 (26). – С. 225–228.
4. Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика» / Т.А. Гулай, В.А. Жукова, С.В. Мелешко, И.А. Невидомская; СтГАУ. – Ставрополь: Сервисшкола, 2016.
5. Элементы теории вероятностей случайных событий: Рабочая тетрадь / И.А. Невидомская, С.В. Мелешко, Т.А. Гулай. – Ставрополь: Сервисшкола, 2015.
6. Теория вероятностей для экономических специальностей на базе Excel (практикум) / А.Ф. Долгополова, О.В. Морозова, Е.В. Долгих, Р.В. Крон, Н.Н. Тынянко, С.В. Попова, Н.Б. Смирнова // Международный журнал экспериментального образования. – 2009. – № S4. – С. 19.
Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события [1, 3].
Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных [5].
Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.
Попробуем составить собственный алгоритм для решения задач по теории вероятности [2, 4]:
1. Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.
2. Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.
3. Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.
4. Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.
5. Готово, вероятность найдена.
Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.
Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене [6].
Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».
Решение. В первую очередь, определим ключевой вопрос задачи – вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.
Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.
Эта вероятность будет равна
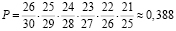
Первая дробь 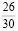
Вторая дробь 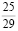
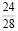
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.
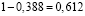
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет – если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?
Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.
Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие 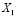
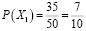
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:
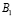
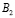
Событие 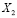
1) Можно предположить, что Жора с вероятностью
забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:
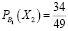
2) Допустим, что Жора с вероятностью
«спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:
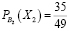
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:
Вероятность не изменилась.
Рассмотрим следующее событие 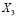
В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности
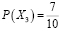
И так далее.
Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот – «несчастливые».
Математика и «чистый эксперимент» – это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.
В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.
Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.
В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».
Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.
Библиографическая ссылка
Ревегук Ю.А., Рудикова Е.С. ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «СЧАСТЛИВОГО» БИЛЕТА НА ЭКЗАМЕНЕ // Международный студенческий научный вестник. – 2018. – № 3-1.
;
URL: https://eduherald.ru/ru/article/view?id=18220 (дата обращения: 12.03.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Библиографическое описание:
Петров, Р. С. Вероятность сдачи ЕГЭ методом угадывания правильного ответа / Р. С. Петров, Б. З. Назримадов, Н. Н. Романова. — Текст : непосредственный // Юный ученый. — 2020. — № 4 (34). — С. 67-70. — URL: https://moluch.ru/young/archive/34/1985/ (дата обращения: 12.03.2023).
Единый государственный экзамен (ЕГЭ) — это один из видов государственной итоговой аттестации по образовательным программам среднего общего образования (ГИА), которую пишут все без исключения выпускники одиннадцатых классов российских средних учебных заведений. Первая часть экзамена — это тест, т. е. выбор правильного(-ых) варианта(-ов) ответа(-ов) из нескольких предложенных. Если вы не знаете ответа, вам остаётся положиться на свою интуицию… Однако реально ли получить высокий балл, попросту расставляя ответы наобум?
Ключевые слова:
ЕГЭ, теория вероятностей, вероятность сдачи ЕГЭ, экзамен, тест.
Актуальность исследования:
данное исследование будет актуально в основном для учащихся 11-х классов, так как оно даст ответ на довольно важный вопрос: насколько хорошо можно написать ЕГЭ, не готовясь к нему? Кажется, как можно «предвидеть» наступление такого случайного события, как правильно данный ответ? Оно ведь может произойти, а может и нет… Но математика нашла способы оценивать вероятность наступления таких событий.
Цель
: определить вероятность сдачи ЕГЭ при помощи угадывания правильного ответа, применяя теорию вероятностей
Объект исследования:
теория вероятностей
Предмет исследования
: практическое применение теории вероятностей
Задачи
:
- Изучить задания первой части (теста) из ЕГЭ
- Выявить вероятность сдачи ЕГЭ методом угадывания ответов
Гипотеза
: предположим, что невозможно сдать ЕГЭ, просто расставляя ответы в первой части «наугад»
Методы исследования
:
- Изучение литературы и других источников информации
- Анализ и синтез
- Идеализация
- Изучение и обобщение
Единый государственный экзамен
Основные сведения о
ЕГЭ
Единый государственный экзамен (ЕГЭ) является одним из видов государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.
При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой наборы из заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.
Чтобы получить аттестат, выпускникам необходимо сдать ЕГЭ по двум обязательным предметам — русскому языку и математике (базового или профильного уровня). ЕГЭ по остальным учебным предметам они сдают по своему выбору.
Структура ЕГЭ
Задания ЕГЭ (КИМы) разрабатываются
Федеральным институтом педагогических измерений
[6].
Примерная структура, форма и содержание КИМов предопределены и не могут быть изменены произвольным образом, а регламентируется они тремя документами, утверждаемыми Рособрнадзором каждую осень: кодификаторами, спецификациями и демоверсиями экзаменов. КИМы включают в себя задания с кратким и развернутым ответами.
В экзаменах по математике базового и профильного уровней нет заданий с выбором ответа: следовательно, для сдачи данных экзаменов способ расстановки ответов «наугад» не подходит меньше всего.
При проведении ЕГЭ по иностранным языкам в состав экзамена входит раздел «говорение», устные ответы на задания которого записываются на аудионосители.
Теория вероятностей
Теория вероятностей — это раздел математики, который изучает числовые характеристики вероятности появления некоторого случайного события в конкретных условиях, которые могут быть многократно воссозданы (как, например, сдача ЕГЭ).
Для событий, вероятность которых находиться по формуле классической вероятности, может быть применён статистический подход. Это было обосновано ещё швейцарским математиком Якобом Бернулли (1655–1705).
Являясь математической основой статистики, теория вероятностей имеет большое значение для множества видов деятельности человека, включающих количественный анализ данных, таких как: социологические исследования, экономический анализ и др.
За последние десятилетия теория вероятностей стала развивающейся наукой со множеством возможных направлений применения.
Вероятность события
В так называемых
случайных
[1]
явлениях существуют определённые закономерности. Задачей теории вероятности является установление таких закономерностей.
Классическое определение вероятности: вероятность события А (обозначается Р(А)) равна отношению числа благоприятствующих исходов к числу всех возможных исходов. Т. е. вероятность события А вычисляется по формуле: Р(А)=n/m, где n ≤ m и n, m є N, из чего следует, что 0 ≤ Р(А) ≤ 1. В данной формуле: n — число благоприятствующих исходов, m — число всех исходов испытания.
Однако в нашей жизни встречаются ситуации, где без практики определить число благоприятных исходов очень трудно, а то и вовсе невозможно.
Например, не подбрасывая кнопку много раз, трудно определить, равновозможны ли ее падения на плоскую часть или на иглу. В подобных случаях и используется статистическое определение вероятности.
Статистическая вероятность
Статистическая вероятность — это числовое выражение степени возможности наступления некоторого события (или того, что данное событие не наступит). Одним из способов, помогающих её рассчитать, является использование формулы Бернулли, позволяющей найти вероятность появления события A при нескольких независимых испытаниях.
Чтобы найти, каков шанс наступления события А при помощи формулы Бернулли, нам надо:
– найти общее количество исходов рассматриваемой ситуации;
– найти количество всех возможных исходов, при которых произойдёт событие А;
– найти, какую часть составляют возможные исходы, при которых произойдёт событие А, от общего количества исходов
Определение вероятности сдачи ЕГЭ
Вероятность сдачи ЕГЭ
Согласно нашим наблюдениям, у учащихся старших классов часто возникают мысли, что можно выбрать ответ наугад и при этом получить высокий балл за экзамен. Но так ли это?
Ответить на этот вопрос мы планируем, используя методы из теории вероятностей. А в качестве объекта для анализа мы решили выбрать ЕГЭ по истории, который сдаём сами.
По данному предмету экзамен включает 14 заданий с выбором ответа. Чтобы сдать экзамен, нужно набрать больше или ровно 32 балла.
Определить вероятность сдачи экзамена (о получении «высокого балла» для поступления в вуз, как мы понимаем, речи не идёт) можно по формуле Бернулли.
Если проводится n независимых испытаний, в результате каждого из которых событие A наступает с вероятностью P(A)=p и не наступает с вероятностью q (q=P(А)=1-p). Вероятность того, что в результате n независимых испытаний событие A наступит ровно k раз равна количеству сочетаний из n по k:
При этом все испытания независимы, а их исходы несовместимы (событие A либо наступает, либо нет). Из этого следует, что вероятность получения удовлетворяющей комбинации будет равна:
Чтобы найти вероятность того, что в n испытаниях событие A наступит k раз, нужно сложить вероятности получения всех удовлетворяющих комбинаций
(они одинаковы и равны).
Тогда количество комбинаций равно
. Получим, что:
— это и есть формула Бернулли.
В итоге мы имеем 14 вопросов. Вероятность угадывания правильного ответа на отдельный вопрос одинакова и равна 1/4 = 0.25 (количество удовлетворяющих исходов (дан правильный ответ) ко всем возможным (всего 4 варианта ответа)). Получаем:
P = P(14) = C
14
14
*0.25
14
*0.75
0
= 0,0000000037252902984619140625 — данное число и является числовым выражением вероятности сдачи ЕГЭ методом угадывания правильного ответа.
Заключение
Как мы можем видеть, вероятность сдать ЕГЭ по истории методом случайной расстановки ответов практически равна нулю. Судя по количеству тестовых заданий в ЕГЭ по другим предметам, утверждение, что сдать его методом угадывания правильного ответа невозможно, справедливо для всех предметов, которые доступны для сдачи выпускниками 11-х классов.
Литература:
- Аджиева А. А., Кибишева А. Р. Формула Бернулли // Вестник научных конференций. — ООО Консалтинговая компания Юком, 2016. — №. 4–3. — С. 17–18.
-
Википедия [электронный ресурс] // Единый государственный экзамен URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Единый
_
государственный
_
экзамен
-
Википедия [электронный ресурс] // Формула Бернулли URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Формула
_
Бернулли
-
Википедия [электронный ресурс] // Бернулли, Якоб URL:
https
://
ru
.
wikipedia
.
org
/
wiki
/
Бернулли
,_
Якоб
-
4ege [электронный ресурс] // Шкала перевода баллов ЕГЭ 2020 URL:
https
://4
ege
.
ru
/
novosti
—
ege
/4023-
shkala
—
perevoda
—
ballov
—
ege
.
html
- О нас // Федеральный институт педагогических измерений. URL: http://www.fipi.ru/about (дата обращения: 21.03.2020).
[1]
Событие называют случайным, если оно либо происходит, либо не происходит
Основные термины (генерируются автоматически): теория вероятностей, правильный ответ, вероятность сдачи ЕГЭ, ЕГЭ, единый государственный экзамен, вероятность, задание, исход, ответ, событие.
Похожие статьи
Взаимосвязь теории вероятности и случайных событий
Когда студент идет на экзамен, вероятность получения им хорошей оценки зависит от
Зарождение теории вероятностей и формирование первых понятий этой ветви математики
При этом вероятности до проведения опыта и после проведения должны совпадать.
Особенности решения текстовых задач в вариантах ЕГЭ по…
Выполнение вариантов единого государственного экзамена предполагает умение сконцентрироваться на полученном задании, внимательность к его выполнению, способность определять главное в большом потоке полученной информации…
Конструирование электронных учебных материалов по…
‒ степень поддержки: исправляются неверные ответы в заданиях или добавляются новые задания по требованию; ‒ интерфейс системы и условия генерируемых заданий могут быть русскими или иностранными; ‒ наличие возможности создания собственных заданий или…
Типология текстовых задач в Едином государственном экзамене…
Решение текстовых задач — одно из базовых умений, необходимое для успешной сдачи единого государственного экзамена. Чаще всего сложности при их решении возникают при составлении уравнения из данных задачи.
Об автоматизации процедуры проведения единого…
Аннотация. В статье проанализирована процедура проведения Единого государственного экзамена (ЕГЭ). Неэффективность использования современных информационных технологий в процедуре ЕГЭ в настоящее время приводит к большим затратам времени и средств…
Единый государственный экзамен: достоинства и недостатки
Про достоинства и недостатки ЕГЭ говорилось и говорится много. К достоинствам относят равные возможности для поступления учащихся в любые
Преимуществом Единого экзамена являются также одновременное его проведение и задания, одинаковые для всех выпускников.
Некоторые факты об успешной подготовке к ЕГЭ
Итоговой аттестацией школьного курса математики является сдача единого государственного экзамена (ЕГЭ).
Проанализировав задания варианта ЕГЭ можно отметить следующие темы курса школьной математики, затронутые в проверке знаний: решение текстовых задач на…
Внеклассное мероприятие «Акция «100 баллов для Победы»
ЕГЭ — это сложно, но можно», который добавил выпускникам заряд позитивной энергии и сил
Проанализировав задания варианта ЕГЭ можно отметить следующие темы курса школьной
Единый государственный экзамен можно считать особым тестом достижений школьников…
Три основных действия с процентами. Математика вокруг нас
— получить представление об экзаменационных заданиях на проценты
Чтобы правильно сориентироваться в этих жизненных ситуациях, нужно хорошо уметь решать задачи на проценты.
Математика с теорией вероятностей и статистикой. ЕГЭ-2014.
Муниципальное бюджетное общеобразовательное учреждение
“СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №6”
Елабужского муниципального района Республики Татарстан

Проектная работа
по математике
ВЕРОЯТНОСТЬ СДАЧИ ОГЭ ПО МАТЕМАТИКЕ
БЕЗ ПОДГОТОВКИ
Авторы:
Загудаев Кир,
Милюков Александр,
ученики 9 класса В
Научный руководитель:
Тутубалина Валентина Андреевна,
учитель математики
Оглавление
Введение…………………………………………………………………………..3
Глава I.
-
История возникновения теории вероятности………………………………5
1.2 Средневековая Европа и начало Нового времени………………………….6
1.3. Теория вероятностей…………………………………………………………7
1.4. Применение теории вероятности……………………………………………9
1.4.1. Применение теории вероятности в астрономии………………………….9
1.4.2. Применение теории вероятности в физике……………………………….9
1.4.3. Применение теории вероятности в биометрии………………………….10
1.4.4. Применение теории вероятности в сельском хозяйстве………………..10
1.4.5. Применение теории вероятности в промышленности………………….10
1.4.6. Применение теории вероятности в медицине…………………………..11
1.4.7. Применение теории вероятности в экономике и банковском деле……11
Глава II.
2.1. ОГЭ как пример использования теории вероятностей жизни……………11
2.1.1. Первый этап практического исследования «Опрос одноклассников»…12
2.1.2. Второй этап практического исследования «Анализ успеваемости девятиклассников»………………………………………………………………12
2.1.3. Третий этап практического исследования «Экспериментальный тест»13
2.1.4. Четвертый этап практического исследования «Расчет вероятности сдачи ОГЭ по формуле Бернули»………………………………………………13
2.2. Памятка «Сдать ОГЭ на 5? Легко!»………………………………………..14
Заключение………………………………………………………………………15
Список литературы…………………………………………………………….16
Приложения
Введение
«Без учёта влияния случайных явлений
человек становится бессильным
управлять развитием интересующих его процессов
в желательном для него направлении»
Актуальность. На 2022 год нам предстоит сдавать основной государственный экзамен. И главные герои предстоящего ОГЭ мы – нынешние восьмиклассники, но об этом, увы, знают только родители и учителя. К сожалению, большинство ребят отмахиваются от родителей и учителей, как от назойливых мух. Чем выше у наших одноклассников успеваемость, тем больше у них ложной самоуверенности: «Я все сдам и так, у меня же пятерка по математике, русскому и т. д.». Среди наших ребят есть и такие. Школьники не осознают, насколько это важно — успешно сдать экзамены, поэтому не уделяют должного внимания подготовке, надеясь на случайный фактор. Однако, мы считаем, что процедура прохождения ОГЭ – деятельность сложная, отличающаяся от привычного опыта учеников и предъявляющая особые требования к уровню подготовки.
Почему при одинаковом уровне знаний одни сдают экзамены лучше, чем другие? В чем могут быть причины? «Везение, удача», – думают некоторые не только школьники, но и их родители. Не только, и не столько!
Проблема. Четвертую четверть седьмого класса и часть второй четверти восьмого класса мы обучались дистанционно. Большинство наших сверстников не усваивали материал и у них сейчас по предметам возникают проблемы. Поэтому мы засомневались «Сможем, ли мы сдать ОГЭ на нужную оценку, или нет?» и «Возможно ли сдать ОГЭ по математике без подготовки?»
Случай – с ним мы встречаемся повседневно. Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться! Но математика нашла способы оценивать вероятность наступления случайных событий. Они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
В 9 классе мы только в конце учебного года будем изучать случайные величины и вычисление вероятности, но мы захотели уже сейчас рассмотреть их подробнее и ответить на заданные нами вопросы.
Гипотеза вероятность угадать верные ответы на ОГЭ очень мала, а значит практически невозможно сдать экзамен без подготовки.
Объект исследования: теория вероятностей.
Предмет исследования: практическое применение теории вероятностей.
Цель исследовательской работы: выявление вероятности успешной сдачи экзамена по математике в 9 классе путем угадывания правильного ответа, применяя теорию вероятностей.
Задачи:
-
собрать, изучить и систематизировать материал о теории вероятностей, воспользовавшись различными источниками информации;
-
рассмотреть использование теории вероятности в различных сферах жизнедеятельности;
-
провести опрос среди учеников 9-х классов МБОУ – СОШ №6;
-
провести исследование по определению вероятности получения; положительной оценки при сдаче ОГЭ путем угадывания правильного ответа;
-
проанализировать полученные данные сделать выводы.
Методы исследования:
-
анализ теоретической литературы;
-
математические расчеты;
-
опрос;
-
эксперимент;
-
сопоставление полученных данных
Новизна исследования состоит в том, что в нашей школе еще никто не определял вероятность сдачи ОГЭ по математике без подготовки, а простым путем угадывания ответов.
Практическая значимость состоит в том, что наша работа может служить стимулом для сверстников к более ответственной подготовке к предстоящим экзаменам. Кроме этого мы рассматриваем возможность использования нашего материала на уроках алгебры, как примера применения вероятности на практике. На классных часах, для повышения ответственности при подготовке к экзамену, мы познакомили с результатами исследования своих одноклассников и ребят из параллельного класса. Считаем, что трансляция нашего материала для широкой аудитории — это наш практический вклад в решение проблемы низкой мотивации учащихся к подготовке к ОГЭ.
Источниковую базу исследования составили 6 книг: И. В. Ященко » 36 вариантов, издательство «Национальное образование, И. В. Ященко, Л. О. Рослова и др. 3000 задач с ответами, издательство «Экзамен». Все задания части 1, Л. Н. Халяпина. Теоретический материал для выполнения заданий ОГЭ первой части, С. В. Драбкина, Д. И. Субботин «Готовимся к итоговой аттестации», издательство «Интеллект-Центр», Л. Молдинов «Как случай управляет нашей жизнью», издательство «Гаятри», Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 9 класс.
Глава I.
-
История возникновения теории вероятности
Французский дворянин, некий господин де Мере, был азартным игроком в кости и страстно хотел разбогатеть. Он затратил много времени, чтобы открыть тайну игры в кости. Он выдумывал различные варианты игры, предполагая, что таким образом приобретет крупное состояние. Так, например, он предлагал бросать одну кость по очереди 4 раза и убеждал партнера, что по крайней мере один раз выпадет при этом шестерка. Если за 4 броска шестерка не выходила, то выигрывал противник.
В те времена еще не существовала отрасль математики, которую сегодня мы называем теорией вероятностей, а поэтому, чтобы убедиться, верны ли его предположения, господин Мере обратился к своему знакомому, известному математику и философу Б. Паскалю с просьбой, чтобы он изучил два знаменитых вопроса: первый из которых он попытался решить сам. Вопрос был такой: «Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний. Паскаль не только сам заинтересовался этим, но и написал письмо известному математику П. Ферма, чем спровоцировал его заняться общими законами игры в кости и вероятностью выигрыша [6]
Таким образом, азарт и жажда разбогатеть дали толчок возникновению новой чрезвычайно существенной математической дисциплины: теории вероятностей (Приложение 1)
1.2 Средневековая Европа и начало Нового времени
В обширной математической энциклопедии «Сумма арифметики, геометрии, отношений и пропорций» итальянца Луки Пачоли (1494) содержатся оригинальные задачи на тему: как разделить ставку между двумя игроками, если серия игр прервана досрочно.
Крупный алгебраист XVI века Джероламо Кардано посвятил анализу игры содержательную монографию «Книга об игре в кости» (1526 год, опубликована посмертно). Кардано провёл полный и безошибочный комбинаторный анализ для значений суммы очков и указал для разных событий ожидаемое значение доли «благоприятных» событий. Кардано сделал проницательное замечание: реальное количество исследуемых событий может при небольшом числе игр сильно отличаться от теоретического, но чем больше игр в серии, тем доля этого различия меньше. По существу, Кардано близко подошёл к понятию вероятности: итак, имеется одно общее правило для расчёта: необходимо учесть общее число возможных
выпадений и число способов, которыми могут появиться данные выпадения,
а затем найти отношение последнего числа к числу оставшихся возможных выпадений.
Исследованием данной темы занимался и Галилео Галилей, написавший трактат «О выходе очков при игре в кости» (1718 год, опубликован посмертно). Изложение теории игры у Галилея отличается исчерпывающей полнотой и ясностью. В своей главной книге «Диалог о двух главнейших системах мира, Птолемеевой и Коперниковой». Галилей также указал на возможность оценки погрешности астрономических и иных измерений, причём заявил, что малые ошибки измерения вероятнее, чем большие, отклонения в обе стороны равновероятны, а средний результат должен быть близок к истинному значению измеряемой величины. Эти качественные рассуждения стали первым в истории предсказанием нормального распределения ошибок.
В разработке основ теории вероятности принимали участие математики такого масштаба, как Паскаль и Ферма, Гюйгенс (1629—1695), который написал тракта «О расчетах при азартных играх», Яков Бернулли (1654—1705), Муавр (1667—1754), Лаплас (1749— 1827), Гаусс (1777—1855) и Пуассон (1781—1840).
В наше время теория вероятности используется почти во всех отраслях знаний: в статистике, синоптике (прогноз погоды), биологии, экономике, технологии, строительстве и т. д. [6]
1.3. Теория вероятностей
При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события. В них различают: достоверные, случайные, невозможные, равновероятные.
Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1, 2, 3, 4, 5, 6 при одном бросании игральной кости.
Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Например, при однократном бросании игральной кости может выпасть число 1 или не выпасть, т.е. событие является случайным.
Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.
Вероятность события А обозначается буквой Р(А) формула записывается так: Р(А)= m/n, где m ≤n. Из формулы следует, что 0≤ Р(А)≤ 1.
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу исходов n всех исходов испытания – классическое определение вероятности [1]
Классическое определение вероятности используется для выявления благоприятных исходов теоретическим путем (Приложение2)
Но встречаются случаи, когда без практики определить число благоприятных исходов невозможно. Например, без многократного подбрасывания кнопки, трудно определить, равновозможны ли ее падения на «на плоскость» или на «острие». В таких случаях используется статистическое определение вероятности.
Статистическая вероятность (частота, относительная частота) – это отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний.
Формула Бернулли — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях.
Чтобы найти каковы шансы наступления события А в данной ситуации, необходимо:
найти общее количество исходов этой ситуации;
найти количество возможных исходов, при которых произойдёт событие А;
найти, какую часть составляют возможные исходы от общего количества исходов. (Приложение2) [5]
1.4. Применение теории вероятности
В 19 и 20 столетиях теория вероятностей проникает сначала в науку (астрономию, физику, биологию), потом в практику (сельское хозяйство, промышленность, медицину), и наконец, после изобретения компьютеров, в повседневную жизнь любого человека, пользующегося современными средствами получения и передачи информации. Проследим применение в различных областях (Приложение 2)
1.4.1. Применение теории вероятности в астрономии
Именно для использования в астрономии был разработан знаменитый “метод наименьших квадратов” (Лежандр 1805, Гаусс 1815). Главной задачей, для решения которой он был первоначально использован, стал расчет орбит комет, который приходилось производить по малому числу наблюдений. Ясно, что надежное определение типа орбиты (эллипс или гипербола) и точный расчет ее параметров оказывается трудным, так как орбита наблюдается лишь на небольшом участке. Метод оказался эффективным, универсальным, и вызвал бурные споры о приоритете. Его стали использовать в геодезии и картографии. Сейчас, когда искусство ручных расчетов утрачено, трудно представить, что при составлении карт мирового океана в 1880-х годах в Англии методом наименьших квадратов была численно решена система, состоящая из примерно 6000 уравнений с несколькими сотнями неизвестных [7]
1.4.2. Применение теории вероятности в физике
Во второй половине 19 века в работах Максвелла, Больцмана и Гиббса была развита статистическая механика, которая описывала состояние разряженных систем, содержащих огромное число частиц (порядка числа Авогадро). Если раньше понятие распределения случайной величины было преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались самые разные величины – скорости, энергии, длины свободного пробега.
1.4.3. Применение теории вероятности в биометрии
В 1870-1900 годах бельгиец Кетле и англичане Френсис Гальтон и Карл Пирсон основали новое научное направление – биометрию, в которой впервые стала систематически и количественно изучаться неопределенная изменчивость живых организмов и наследование количественных признаков. В научный оборот были введены новые понятия – регрессии и корреляции.
Итак, вплоть до начала 20 века основные приложения теории вероятности были связаны с научными исследованиями. Внедрение в практику – сельское хозяйство, промышленность, медицину произошло в 20 веке [7]
1.4.4. Применение теории вероятности в сельском хозяйстве
В начале 20 века в Англии была поставлена задача количественного сравнения эффективности различных методов ведения сельского хозяйства. Для решения этой задачи была развита теория планирования экспериментов, дисперсионный анализ. Основная заслуга в развитии этого уже чисто практического использования статистики принадлежит сэру Рональду Фишеру, астроному по образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского общества. Современная математическая статистика, пригодная для широкого применения в практике, была развита в Англии (Карл Пирсон, Стьюдент, Фишер). Стьюдент впервые решил задачу оценки неизвестного параметра распределения без использования байесовского подхода [7]
1.4.5. Применение теории вероятности в промышленности
Введение методов статистического контроля на производстве (контрольные карты Шухарта). Сокращение необходимого количества испытаний качества продукции. Математические методы оказываются уже настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после окончания второй мировой войны в 1947 году.
1.4.6. Применение теории вероятности в медицине
Широкое применение статистических методов в медицине началось сравнительно недавно (вторая половина 20 века). Развитие эффективных методов лечения (антибиотики, инсулин, эффективная анестезия, искусственное кровообращение) потребовало достоверных методов оценки их эффективности. Возникло новое понятие “Доказательная медицина”.
С середины 1980-х годов возник новый и важнейший фактор, революционизировавший все приложения теории вероятностей – возможность широкого использования быстрых и доступных компьютеров. Почувствовать всю громадность произошедшего переворота можно, если учесть, что один современный персональный компьютер превосходит по быстродействию и памяти все компьютеры СССР и США, имевшиеся к 1968 году, времени, когда уже были осуществлены проекты, связанные со строительством атомных электростанций, полетами на Луну, созданием термоядерной бомбы [7]
1.4.7. Применение теории вероятности в экономике и банковском деле
Широкое применение имеет теория риска. Теория риска есть теория принятия решений в условиях вероятностной неопределенности. С математической точки зрения она является разделом теории вероятностей, а приложения теории риска практически безграничны. Наиболее продвинута финансовая область приложений: банковское дело и страхование, управление рыночными и кредитными рисками, инвестициями, бизнес-рисками, телекоммуникациям. Развиваются и нефинансовые приложения, связанные с угрозами здоровью, окружающей среде, рисками аварий и экологических катастроф, и другими направлениями.
Глава II.
2.1. ОГЭ как пример использования теории вероятностей жизни
Среди учеников часто возникает вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен?»
Ответить на этот вопрос можно путем использования теории вероятностей. Мы хотим проверить это на примере обязательных для сдачи ОГЭ предметов математики.
Наше исследование состоит из четырех этапов [2]
2.1.1.Первый этап практического исследования
«Опрос учащихся 8 и 9 классов»
В опросе приняли участие 13 учащихся 8 класса и 17 учащихся 9 класса.
На первом этапе нашего исследования мы провели опрос среди одноклассников:
«Как вы считаете, можно ли сдать экзамен, по математике, без подготовки методом угадывания?»
Результат: 9 ребят из 13 считают, что таким способом можно сдать и математику (Приложение 4)
Затем мы задали такой же вопрос учащимся 9 класса (Приложение 5)
Результат: 15 учащихся из 17 считают, что методом угадывания и без подготовки сдать экзамен по математике невозможно.
Следующий вопрос: «Готовитесь ли вы дополнительно для сдачи ОГЭ по математике?»
Результат: 6 учеников из 13 ответили, что они к экзамену по математике дополнительно не готовятся.
На вопрос: «Вы настолько уверены в своих силах, что сдадите ОГЭ без подготовки?», школьники ответили, что они надеются списать.
Таким образом, в отличие от учащихся 8 класса 80% учащихся 9 класса уверены, что готовиться к экзамену по математике необходимо, но все-таки 20% ребят надеются, что им удастся списать ответы на задания. Уверены, что после того, как мы познакомили наших одноклассников с результатами своей работы, они изменят свое мнение о подготовке к ОГЭ.
2.1.2. Второй этап практического исследования
«Анализ успеваемости девятиклассников»
Далее мы проанализировали оценки за контрольные работы и пробный экзамен по математике у девятиклассников МБОУ – Елабужской СОШ №6.
Результат: 28% учащихся 9-х классов не справились с пробным экзаменом ОГЭ. 57% учащихся написали пробный ОГЭ по математике хуже, чем они пишут текущие контрольные работы (Приложение 6)
2.1.3. Третий этап практического исследования
«Экспериментальный тест»
В интернете мы прочитали теорию, что можно удовлетворительно сдать тестовую работу, если в каждом вопросе выбирать один и тот же номер из предложенных ответов.
На этом этапе мы провели эксперимент среди учащихся 8а класса. В эксперименте участвовали 9 школьников. Всем был предложен один и тот же тест по алгебре «Свойства арифметических корней» из 10 вопросов с выбором ответа. Первый вариант (5 учащихся) отвечали наугад, второй вариант (5 учащихся) тоже отвечали наугад, но выбирали не разные варианта ответа, а отмечали только какой – то один. Например, везде отмечали только первый ответ из предложенных четырех, или только третий ответ из предложенных четырех (Приложение 7) [4]
Результат: с работой лучше справились одноклассники первого варианта. Из 4 человек 1 школьник набрал 5 баллов и справился с работой на «3». Во втором варианте 5 ребят набрали максимум по три балла. (Приложение 
Теория, которую мы прочитали, на практике не подтвердилась. Значит, отвечая на тестовые вопросы больше шансов ответить на удовлетворительную отметку путем беспорядочного ответа, чем путем выбора одного и того же ответа. Хотя и она равна 0,1
2.1.4. Четвертый этап практического исследования
«Расчет вероятности сдачи ОГЭ по формуле Бернули»
Первая часть экзаменационной работы по математике состоит из 19 заданий. С выбором ответа предложено пять заданий. Каждое задание имеет 4 варианта ответов, один из которых правильный. Чтобы сдать экзамен, нужно набрать не менее 8 баллов. Мы решили убедиться в этом и определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли.
Каждый вопрос имеет 4 варианта ответа, поэтому вероятность ответить правильно у нас равна 1/4, а ответить не правильно 1-1/4=3/4
Сначала запишем формулу числа сочетаний
С8(5) = 8!/3!*5! = 56
Подставим ее в формулу Бернулли и вычислим Вероятность угадывания всех правильных ответов:
Р8(5)= 56* ¼5 *3/43 = 56*1/1024*81/64 = 567/8192 = 0,06921387
Умножим на 100% = 6% — вероятность угадать ответы в этих 5 вопросах.
Но по классической вероятности, даже, если угадать правильные ответы во всех 5 вопросах получим 5/8 = 0,16
Значит, вероятность сдать ОГЭ очень мала.
Результат: вероятность сдать ОГЭ по математике равна 0,06921387, а это еще раз подтверждает то, что без подготовки, только методом угадывания экзамен по математике сдать невозможно.
2.2. Памятка «Сдать ОГЭ на 5? Легко!»
Проанализировав результаты исследования, мы разработали для наших одноклассников и ребят из параллельного класса в помощь в подготовке к ОГЭ памятку «Сдать ОГЭ на 5? Легко!»
-
Распределить все предметы, подлежащих сдачи ОГЭ, между днями недели для отработки тестов, используя средства интернета.
-
Привлечь к контролю родителей.
-
Изучать новый материал на уроках и закреплять дома.
-
Выполнять домашние задания, которые дают учителя для подготовки к экзаменам.
-
По мере возможности записаться на курсы по подготовке к ОГЭ.
-
Закреплять свою память.
-
Выполнять режим дня (чередование умственной деятельности с отдыхом).
-
Изучать теоретический и практический материал регулярно и в системе, а не только перед экзаменом.
Заключение
В своей работе мы привели неопровержимые доказательства нашей гипотезы: «Вероятность угадать верные ответы на ОГЭ очень мала, а значит практически невозможно сдать экзамен без подготовки»
Как оказалось, большинство наших одноклассников не осознают, что получить хорошую оценку за экзамен можно только при систематической подготовке. Считаем, что самооценка у них завышенная.
28% девятиклассников в этом учебном году имеют мало шансов сдать экзамены без предварительной подготовки, а значит, и получить аттестат. 30% девятиклассников надеются, что им удастся списать ответы на задания.
Вероятность сдачи ОГЭ только методом «наугад» ничтожно мала и равна 0,06921387
Проводя исследование по данной теме мы:
-
Изучили теоретический материал. Понятия, которые были нам необходимы для нашей работы, мы нашли в ВИКИПЕДИИ.
-
Провели опрос среди учащихся класса по данной теме и поняли, что многие учащиеся могут не сдать экзамены, так как не прикладывают усилия связанные со знанием правил, тем, понятий, отработкой навыков подготовки
-
Произвели расчеты вероятности сдачи экзамена при наличии ответов по выбору (при условии, если все ответы с их выбором будут правильными).
-
Составили список путей выхода из проблемной ситуации.
-
Познакомили одноклассников с результатами нашего исследования.
-
Попросили классного руководителя Тутубалину В.А. донести информацию до родителей (законных представителей).
Уверены, что после того, как мы познакомили наших одноклассников с результатами своей работы, они изменят свое мнение о подготовке к ОГЭ. Наша работа принесет пользу всем: обучающимся, родителям, учителям.
Таким образом, мы считаем, что цель исследования, которую мы перед собой ставили, нами достигнута и все задачи выполнены.
.
СВ является непрерывной, если
ее функция распределения непрерывна.
Для НСВ наряду с функцией распределения
вводится еще 1 закон распределения –
плотность вероятности.
Определение 4.6:
Плотностью вероятностей хназывается производная ее функции
распределения, т.е.
(плотность вероятностей может быть
обозначена
)
Свойства плотностей вероятности:
1.
2.
3.
4.
— условие нормировки
4.5. Числовые характеристики cb
Определение 4.7:
Математическим ожиданием ДСВназывается число.
Определение 4.8:
Математическим ожиданием НСВназывается число.
математическое
ожидание
Свойства математического ожидания:
1. X = с
= const,
M(C) = C
2. Постоянный множитель выносится за
знак математического ожидания, т.е.:
3. Математическое ожидание суммы СВ
равно сумме математических ожиданий
4.6. Дисперсия случайной величины
Определение 4.9:
Дисперсией СВназывается число:
Свойства дисперсии:
1. Дисперсию можно найти по формуле:
2.
3. Если X = с=const,
тоD(C)
= 0
4. Если
,
то
Формулы:
для ДСВ:
1.
2.
для НСВ:
1.
2.
Средним квадратичным отклонением
СВ Хназывается число:.
Законы распределения СВ (стр.19):
-
Биноминальное распределение.
-
Распределение Пуассона
-
Равномерное распределение
-
Показательное распределение
-
Нормальное распределение
Практическая работа № 2
№ 1.
Для данного студента вероятность
успешной сдачи первого экзамена равна
0,9, второго – 0,8, третьего – 0,7. Случайная
величина х – число успешно
сданных экзаменов. Найти: ряд распределения
ДСВ, математическое ожидание М(Х);
дисперсию D(X);
среднеквадратичное отклонение
.
Решение:
Случайная величина принимает значения:
0, 1, 2, 3
Пусть р1– вероятность
сдачи первого экзамена.
р2– вероятность сдачи
второго экзамена.
р3– вероятность сдачи
третьего экзамена.
q1– вероятность
несдачи первого экзамена.
q2– вероятность
несдачи второго экзамена.
q3– вероятность
несдачи третьего экзамена.
-
Х
0
1
2
3
Р
0,006
0,092
0,398
0,504
(методичка, стр.25, формула для доверительного
интервала)
Нормальное распределение – стр.21
П.6 зад.7 для решения к.р.
№ 2.
На сборку поступили детали с 3 конвейеров.
Первый дает 25%, второй – 30%, третий – 45%
деталей, поступающих на сборку. С первого
конвейера в среднем поступает 2% брака,
со второго – 3%, с третьего – 1%. Найти
вероятность того, что:
-
На сборку поступила бракованная
деталь. -
Поступившая бракованная деталь со
второго конвейера.
Решение:
Пункт 1.
Пусть событие А– поступившая деталь
на сборку – бракованная.
Н1– деталь с первого конвейера.
Н2– деталь со второго конвейера.
Н1– деталь с третьего конвейера.
Пункт 2.
№ 3.
Монету бросают 10 раз. Найти вероятность
того, что герб выпадет:
-
2 Раза.
-
Менее 2 раз.
-
Не менее 2 раз.
Решение:
1:
Вероятность того, что выпадет герб,
;n = 10, k
= 2
Формула Бернулли:
2:
По формуле Бернулли:
3:
Тел. кафедры – 60-27-71
Надежда Николаевна
- Главная→
- Видеоуроки→
- Вероятность сдачи экзамена
Вероятность сдачи экзамена
Экзаменационный билет содержит три вопроса. Верлятность того, что студент ответит на любой вопрос билета, равна 0,9. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса билета.
Данный видео урок предназначен для подготовки учащихся к ЕГЭ, а также для учеников 11 класса при изучении темы: «Случайные события и их вероятности» из раздела «Элементы математической статистики, комбинаторики и теории вероятности».
Интересная статья? Поделитесь ей с другими:
Лучшие цены на образовательные товары. На сайте дешевле, чем в магазинах.
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных и соглашаетесь с Условиями использования.
Горячая линия
8 (800) 100-52-31
I would like to elaborate on AlgorithmsX’ answer. Letting $N $ be the total number of questions to choose from (I.e. 5500) and $K $ the number of questions the user knows the answer to, then AlgorithmsX’ answer explains how to calculate the probability that the exam is passed.
However, we do not know what $K$ is. Just assuming that the fraction of known questions $frac{K}{N}$ is equal to the fraction of correctly answered questions, is not justified. Indeed, suppose that a student answers 45 out of 50 questions correctly. You can’t just assume that he knows exactly 90 percent of the answers to the 5500 questions, he might just have gotten the questions he knew the answer to.
Assuming you do want to give feedback to a user who hasn’t answered all 5500 questions, you need statistics. If you never had statistics, the following might feel backward. Let $m$ be the number of questions answered on the app during a ‘test exam’, $Y$ the number of correctly answered questions on the test exam. Then $Y$ too has a hypergeometric distribution.
$$
P(Y = k) = frac{binom{K}{k}binom{N-K}{m-k}}{binom{N}{m}} \
P(Y geq k) = sum_{i=k}^{m} frac{binom{K}{i}binom{N-K}{m-i}}{binom{N}{m}}
$$
We want a conservative estimate for $K$. One way to find this is to pick the smallest value of $K$ for which the received value of $Y$ is not too improbable. «not too improbable» is subjective: statisticians often interpret this as «with probability at least 5%». I too will use this definition in what follows. Let $y$ be the received value of $Y$, then let $hat{K}$ be the solution of
$$
P(Y geq y) = sum_{i=y}^{m} frac{binom{K}{i}binom{N-K}{m-i}}{binom{N}{m}} = 0.05
$$
rounded to the nearest integer. Solving the above equation requires numerical methods: Google ‘Secant method’ or ask a new question if you do not know how to do this.
You can now state with 95% confidence that the student knows the answer to at least $hat{K}$ questions. You can then proceed to calculate the minimal probability of success using the method described before and with this $hat{K}$ as $K$. Google ‘confidence intervals’ if you want to know more about the method used. This is a lot more complicated than the first answer, so take your time to look some things up and let me know if anything is unclear.
For the sake of completeness I want to point out that two implicit assertions were made:
- Students can only get a question correct if they really know the answer. This assertion is false if the exam is multiple choice and a question can be marked correct because of a lucky guess. Extra calculations are needed to take this effect into account. For your app, I would suggest to encourage users to skip a question when they do not know the answer to avoid overestimating their knowledge because of lucky guesses.
- The value of $K$ is fixed, I.e. students do not learn or forget. In practice, a good app should explain the user why an answer was wrong, thereby hopefully increasing $K$ during the test exam. On the other hand, knowledge can be forgotten. AlgorithmsX mentioned the Forgetting Curve in a comment before.
There is a lot of extra tweaks which can be done, but I think this answer covers the basics: use statistics to estimate the student’s knowledge, then use probability to calculate their odds of succeeding.