Урок посвящен тому, как решать 4 задание ЕГЭ по информатике
Содержание:
- Кодирование информации
- Кодирование и расшифровка сообщений
- Решение 4 заданий ЕГЭ
Кодирование информации
4-е задание: «Кодирование и декодирование информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 2 минуты.
Проверяемые элементы содержания: Умение кодировать и декодировать информацию
До ЕГЭ 2021 года — это было задание № 5 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Из-за невнимательного чтения условия задания экзаменуемые иногда не замечают, что требуется найти кодовое слово минимальной длины с максимальным (минимальным) числовым значением.
Кроме того, если в задании указано, что несколько букв остались без кодовых слов (как, например, в задании демоварианта), то кодовое слово для указанной буквы должно быть подобрано таким образом, чтобы осталась возможность найти кодовые слова, удовлетворяющие условию Фано, и для других букв. Так, например, если мы букву А закодируем нулём, а букву Б единицей, то букву В мы уже никак не сможем закодировать с соблюдением условия Фано, поэтому длину кодового слова для А или Б следует увеличить»
ФГБНУ «Федеральный институт педагогических измерений»
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- Кодирование бывает равномерным и неравномерным:
- при равномерном кодировании всем символам соответствуют коды одинаковой длины;
- при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
- если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
- условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Однозначное декодирование обеспечивается:
Однозначное декодирование
Декодирование
Егифка ©:
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
ЕГЭ 4.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
✍ Решение:
- Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
ВОДОПАД:010010001110010
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Теоретическое решение ЕГЭ данного задания по информатике, видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Рассмотрим еще разбор 4 задания ЕГЭ:
ЕГЭ 4.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
✍ Решение:
- Во-первых, проверяем условие Фано: никакое кодовое слово не является началом другого кодового слова. Условие верно.
- Код разбиваем слева направо согласно данным, представленным в таблице. Затем переведём его в буквы:
✎ 1 вариант решения:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
✎ 2 вариант решения:
-
Этот вариант решения 4 задания ЕГЭ более сложен, но тоже верен.
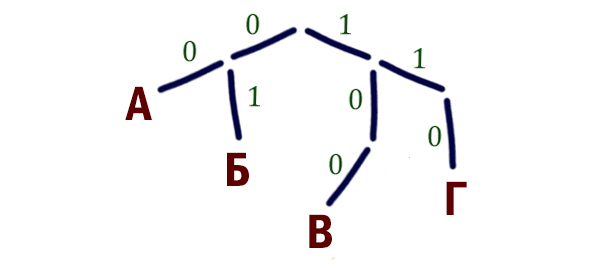
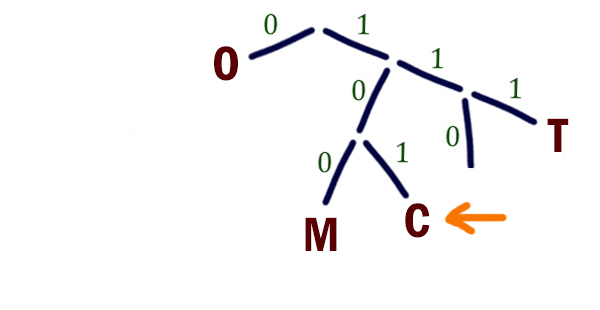
- Сделаем дерево, согласно кодам в таблице:
- Сопоставим закодированное сообщение с кодами в дереве:
110 000 01 001 10
Результат: b a c d e.
Кроме того, вы можете посмотреть видеорешение этого задания ЕГЭ по информатике (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Решим следующее 4 задание:
ЕГЭ 4.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).
Определите, какое число передавалось по каналу в виде 01100010100100100110.
✍ Решение:
- Рассмотрим пример из условия задачи:
Было2310 Стало00101001102
0010100110 (0010 - 2, 0011 - 3)
01100 01010 01001 00110
0110 0101 0100 0011
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видеорешение этого задания ЕГЭ по информатике, теоретическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
ЕГЭ 4.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Подобные задания для тренировки
✍ Решение:
✎
1 вариант решения
основан на логических умозаключениях:
- Найдём самые короткие возможные кодовые слова для всех букв.
- Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
- Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
- Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
- Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
- Будем использовать дерево. Влево откладываем 0, вправо — 1:
- Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
4.5:
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:
А: 101010, Б: 011011, В: 01000
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
- Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
4.6:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:
А - 01 Б - 00 В - 11 Г - 100
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
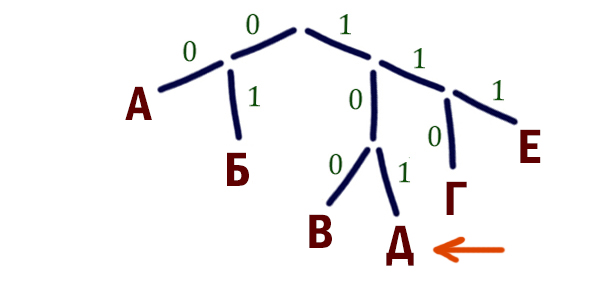
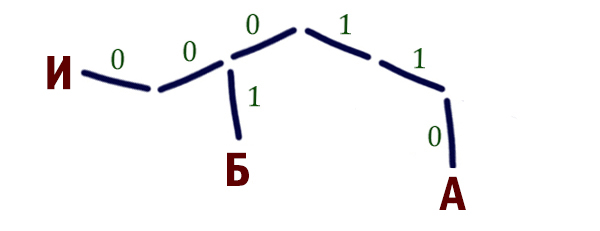
- Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
- Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
- Перепишем сверху вниз получившееся кодовое слово для Д: 101
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
4.7: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100
Подробное теоретическое решение данного 4 (раньше №5) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
4.8:
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
- Получившееся числовое значение кодового слова для буквы Г — 01.
- Получившееся числовое значение кодового слова для буквы Г — 00.
- После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Дерево по условию Фано (однозначно декодируется с начала):
Дерево по обратному условию Фано (однозначно декодируется с конца):
Результат: 00
4.9:
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
Подобные задания для тренировки
✍ Решение:
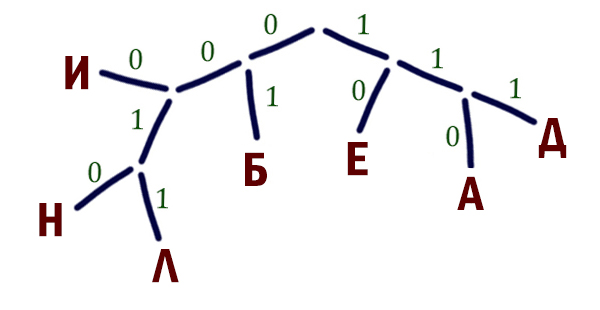
- С помощью дерева отобразим известные коды для букв:
- В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
- Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Результат: 20
Смотрите виде решения задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Всего: 114 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
По каналу связи передаются сообщения, содержащие только восемь букв: К, Л, М, Н, О, П, Р, С. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: К — 001, Н — 100, Р — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МОЛОКОСОС?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Д, О, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 01, Д — 001, Р — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ВОДОВОРОТ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 000, Б — 01, В — 1101, Г — 111, Д — 0010, Е — 100. Для кодирования слова ГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 101, В — 1001, Г — 111, Д — 0110, Е — 110. Для кодирования слова ОГОРОД потребовалось 17 двоичных знаков. Какое кодовое слово соответствует букве О?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 011, Г — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Для кодирования растрового рисунка, напечатанного с использованием шести красок, применили неравномерный двоичный код. Для кодирования цветов используются кодовые слова.
Белый — 0, Зелёный — 11111, Фиолетовый — 11110, Красный — 1110, Чёрный — 10. Укажите кратчайшее кодовое слово для кодирования синего цвета, при котором код будет допускать однозначное декодирование.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Источник: ЕГЭ по информатике 13.06.2019. Основная волна. Юг-Центр.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: В — 1110, Г — 110, Д — 0000, Е — 01. Известно, что для кодирования слова БАОБАБ потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве А?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 10, Г — 1110, Д — 0111, Е — 010. Известно, что для кодирования слова АНАНАС потребовалось 16 двоичных знаков. Какое кодовое слово соответствует букве Н?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 000, Б — 01, В — 1101, Г — 111, Д — 0010, Е — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОКОС?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Источник: Демонстрационная версия ЕГЭ—2016 по информатике.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 011, И — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Для передачи сообщений, составленных из заглавных букв русского алфавита, используется неравномерный двоичный код, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова, назначенные для некоторых букв: А — 000, Б — 0010, В — 101, Г — 11. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово КОЛОБОК?
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову КАША соответствует код 011011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово ОСОКА?
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Д, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 110, Б — 01, И — 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ВВЕДЕНИЕ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 101, В — 1001, Г — 111, Д — 0110, Е — 110. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ЛИЛИЯ?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову УДОД соответствует код 100011101. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово УДАЧА?
По каналу связи передаются сообщения, содержащие только пять букв: A, B, С, D, E. Для передачи используется двоичный код, допускающий однозначное декодирование. Для букв A, B, C используются такие кодовые слова: A — 1, B — 010, C — 000.
Укажите кратчайшее кодовое слово для буквы E, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Всего: 114 1–20 | 21–40 | 41–60 | 61–80 …
Автор материалов — Лада Борисовна Есакова.
Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.
Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.
Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.
Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.
Равномерное кодирование всегда однозначно декодируемо.
Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:
Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.
Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.
Кодирование в различных системах счисления
Пример 1.
Для кодирования букв О, В, Д, П, А решили использовать двоичное представление
чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится
1) 22162
2) 1020342
3) 2131453
4) 34017
Решение:
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для одноразрядных чисел:
|
О |
В |
Д |
П |
А |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Закодируем последовательность букв: ВОДОПАД — 010010001110010.
Разобьём это представление на тройки справа налево и переведём каждую тройку в восьмеричное число.
010 010 001 110 010 — 22162.
Правильный ответ указан под номером 1.
Ответ: 1
Пример 2.
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
1) D3A6
2) 62032206
3) 6A3D
4) CADBAADC
Решение:
Закодируем последовательность букв: ВАГБААГВ — 1101001110100110. Разобьем это представление на четвёрки справа налево и переведём каждую четверку в шестнадцатеричное число:
1101 0011 1010 01102 = D3A616
Правильный ответ указан под номером 1.
Ответ: 1
Расшифровка сообщений
Пример 3.
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
|
a |
b |
c |
d |
e |
|
100 |
110 |
011 |
01 |
10 |
Определите, какой набор букв закодирован двоичной строкой 1000110110110, если известно, что все буквы в последовательности – разные:
1) cbade
2) acdeb
3) acbed
4) bacde
Решение:
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит код можно раскодировать неоднозначно.
Значит, будем перебирать варианты, пока не получим подходящее слово :
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.
Такой вариант удовлетворяет условию, значит, окончательно получили ответ: acdeb.
Ответ: 2
Пример 4.
Для передачи данных по каналу связи используется 5-битовый код. Сообщение содержит только буквы А, Б и В, которые кодируются следующими кодовыми словами: А — 11010, Б — 10111, В — 01101.
При передаче возможны помехи. Однако некоторые ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов отличаются друг от друга не менее чем в трёх позициях. Поэтому если при передаче слова произошла ошибка не более чем в одной позиции, то можно сделать обоснованное предположение о том, какая буква передавалась. (Говорят, что «код исправляет одну ошибку».) Например, если получено кодовое слово 10110, считается, что передавалась буква Б. (Отличие от кодового слова для Б только в одной позиции, для остальных кодовых слов отличий больше.) Если принятое кодовое слово отличается от кодовых слов для букв А, Б, В более чем в одной позиции, то считается, что произошла ошибка (она обозначается ‘х’).
Получено сообщение 11000 11101 10001 11111. Декодируйте это сообщение — выберите правильный вариант.
1) АххБ
2) АВхБ
3) хххх
4) АВББ
Решение:
Декодируем каждое слово сообщения. Первое слово: 11000 отличается от буквы А только одной позицией. Второе слово: 11101 отличается от буквы В только одной позицией. Третье слово: 10001 отличается от любой буквы более чем одной позицией. Четвёртое слово: 11111 отличается от буквы Б только одной позицией.
Таким образом, ответ: АВхБ.
Ответ: 2
Однозначное кодирование
Пример 5.
Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 0001
2) 000
3) 11
4) 101
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.
Ответ: 2
Пример 6.
Для кодирования некоторой последовательности, состоящей из букв У, Ч, Е, Н, И и К, используется неравномерный двоичный префиксный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему остался префиксным? Коды остальных букв меняться не должны.
Выберите правильный вариант ответа.
Примечание. Префиксный код — это код, в котором ни одно кодовое слово не является началом другого; такие коды позволяют однозначно декодировать полученную двоичную последовательность.
1) кодовое слово для буквы Е можно сократить до 01
2) кодовое слово для буквы К можно сократить до 1
3) кодовое слово для буквы Н можно сократить до 10
4) это невозможно
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Легко заметить, что если букву Н перенести в вершину 10, она останется листом. Т.е. кодовое слово для буквы Н можно сократить до 10.
Правильный ответ указан под номером 3.
Ответ: 3
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023
В этом уроке мы поговорим о задании 4 из ЕГЭ по информатике 2022.
Задание 4 включает в себя понятие кодирование и декодирование информации.
Приступим к тренировочным заданиям из ЕГЭ по информатике 2022.
Задача (Стандартная)
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 00, 01, 100, 110. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Используем приём Дерево Фано. Расставим на этом дереве те буквы, для которых уже известны кодовые слова.
Дерево рисуется обычно сверху вниз. В начале от дерева рисуются две ветки: ветка 0 и ветка 1. От каждой ветки можно нарисовать ещё две ветки, так же 0 и 1, и т. д.
Для удобства ветки с 1 будем направлять вправо, а ветки с 0 будем направлять влево.
В конце каждой ветки можно размещать буквы, но если мы разместили букву, то эта ветка блокируется, и от этой ветки больше нельзя делать новые ответвления.
Нам осталось закодировать (расположить на дереве) две буквы: Д и Е.
Мы можем нарастить ещё две ветки от точки 1-1. Тогда получится код 111. И от точки 1-0. Тогда получится код 101.
Для буквы Д нужно выбрать код с наименьшим числовым значением. Значит, для буквы Д выбираем код 101, а для буквы Е выбираем код 111.
Ответ: 101
Закрепим приём дерево Фано на ещё одной примерной задаче из ЕГЭ по информатике 2022.
Задача(Стандартная, закрепление)
Для кодирования некоторой последовательности, состоящей из букв Н, О, П, Р, С, Т, У, Ф решили использовать неравномерный двоичный код, удовлетворяющий условию, что ни одно кодовое слово не является началом другого кодового слова. Для букв Н, О, П, Р, С, Т использовали соответственно кодовые слова 10, 110, 010, 0110, 111, 0111. Укажите кратчайшее возможное кодовое слово для буквы У, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Здесь код так же должен удовлетворять Условию Фано, т.к. сказано, что ни одно кодовое слово не является началом другого кодового слова.
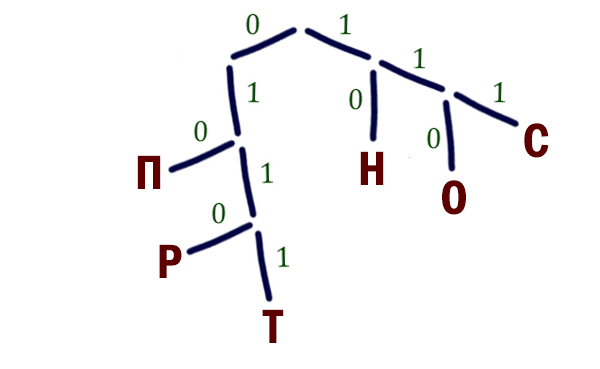
Значит, можем воспользоваться Деревом Фано. Расположим на Дереве Фано буквы, для которых уже известны кодовые слова.
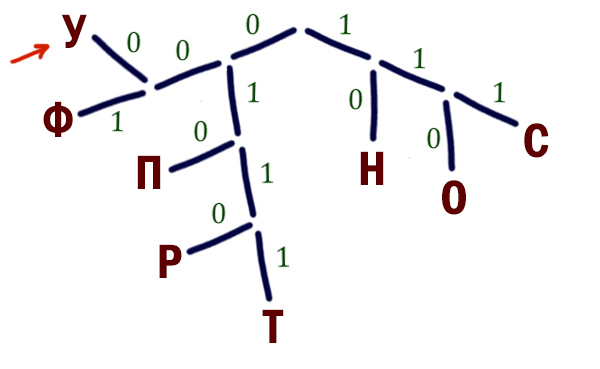
Нам нужно закодировать ещё две буквы: У, Ф. У нас единственная возможность осталась прорастить ветку от точки 0. От этой точки проращиваем ветку 0 и от этой ветки проращиваем ещё две ветки 0 и 1.
Букву У размещаем на позиции 000, потому что для этой буквы нужно выбрать код с наименьшим числовым значением.
Ответ: 000
Ещё одна примерная задача из ЕГЭ по информатике 2022 является частым гостем в различных тренировочных вариантах.
Задача (Стандартная, закрепление)
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Д, Л, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 110, Б – 01, И – 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ?
Решение:
Расставим на дереве Фано буквы, для которых известны коды.
Нам осталось расположить 4 буквы: Д, Л, E, Н.
Буква Е встречается три раза в слове ДЕЛЕНИЕ, значит, ей нужно постараться присвоить самый короткий код. По дереву видно, что можно букве Е присвоить код 10.
Буквы Д, Л, Н встречаются в слове ДЕЛЕНИЕ 1 раз. Одну букву можно разместить на позицию 111. Так же можно продлить ветку из точки 00, а затем от позиции 001 сделать два отростка. У нас получатся ещё два свободных места: 0011 и 0010.
Можно оставшиеся буквы разместить следующим образом:
Подсчитаем какое количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ.
3+2+4+2+4+3+2=20
Ответ: 20
Далее решим непростую задачу из тренировочных вариантов ЕГЭ по информатике 2022. Похожая задача была в сборнике С. С. Крылова в 2021 году.
Задача (Непростая)
По каналу связи передаются сообщения, содержащие только четыре буквы: М, Н, Р, Т; для передачи используется двоичный код, допускающий однозначное декодирование.
Для букв М, Н, Р используются такие кодовые слова: М: 00011, Н: 1001, Р: 01100.
Укажите кратчайшее кодовое слово для буквы Т, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
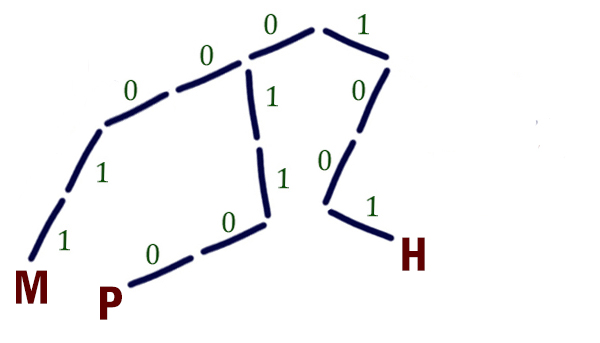
Нужно, чтобы код декодировался однозначно. Чтобы код декодировался однозначно, можно использовать условие Фано. Мы видим, что в уже известных кода не нарушается условие Фано. Узнаем код для буквы Т по дереву Фано. Отметим известные буквы.
Куда разместить букву Т? Чтобы кодовое слово было кратчайшее, разместим букву Т на позицию 11.
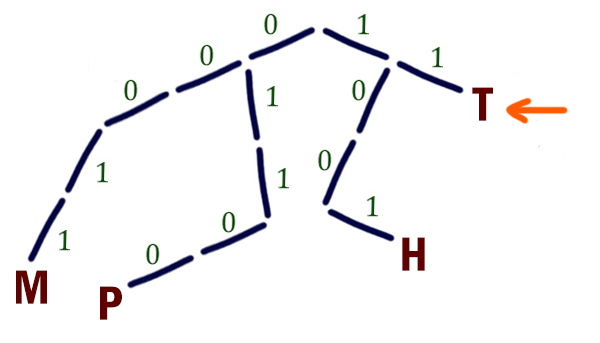
Сложность этой задачи заключается в том, что явно не указано, что нужно использовать условие Фано. Так же однозначное декодирование будет, если используется обратное условие Фано.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Т. е. сообщения нужно такие раскодировать справа налево. Здесь про то, как будут раскодировать сообщения, ничего не сказано, поэтому мы должны проверить, какой код получится для буквы Т, если здесь используется обратное условие Фано.
Кодовое слово 0 мы использовать не можем, потому что 0 — это окончание кодового слова буквы Р. Кодовое слово 1 — это окончание кодовых слов букв М и Н. Кодовое слово 00 — это окончание кодового слова буквы Р. А вот 10 подходит для буквы Т.
Получилась следующая ситуация. Если кодовые слова будут удовлетворяют условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 11 с минимальным числовым значением. Если кодовые слова будут удовлетворяют обратному условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 10 с минимальным числовым значением.
И в том и в другом случае будет однозначное декодирование. Но мы выбираем тот случай, когда кодовое слово будет наименьшим числовым значением. Таким образом, в ответе напишем 10.
Ответ: 10
Разберём ещё один нюанс в подобных задах из ЕГЭ по информатике.
Задача (Ещё раз про однозначное декодирование)
По каналу связи передаются сообщения, содержащие только четыре буквы: М, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, М используются такие кодовые слова: Т: 111, О: 0, М: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Здесь условие похоже на то, которое было в предыдущей задаче. Но обратное условие Фано здесь не применимо, т.к. код для буквы О является окончанием для кода буквы М.
Значит, у нас остаётся единственный инструмент, чтобы сообщения декодировались однозначно — это условие Фано. Теперь задачу решаем как обычно по дереву Фано.
Выбираем из двух вариантов: 110 и 101. Но останавливаемся на 101, т.к. это кодовое слово с наименьшим числовым значением.
Ответ: 101
Решим задачу, которая часто встречается в бумажных сборниках по подготовке к ЕГЭ по информатике.
Задача (код не удовлетворяет условию Фано)
По каналу связи передаются шифрованные сообщения, содержащие только пять латинских букв: A, B, С, D, E. Для передачи используется неравномерный двоичный код. Для некоторых букв известны кодовые слова: A: 01, B: 10, C: 11, D: 000.
Укажите самое короткое кодовое слово для буквы E, при котором код не будет удовлетворять условию Фано, при этом в записи самого этого слова должно использоваться более одного символа, а само слово не должно совпадать ни с одним из используемых слов для букв с известными кодами.
Если таких слов несколько, то укажите слово с наименьшим числовым значением.
Решение:
Здесь код не должен однозначно декодироваться.
Подходит код 00, т.к. длина этого кодового слова больше чем 1 символ. Этот код не совпадает ни с одним кодом для известных букв. Этот код нарушает принцип условия Фано, видно, что он является началом кодового слова буквы D. И этот код имеет самое маленькое числовое значение.
Ответ: 00
В 4 задании из ЕГЭ по информатике 2022 не обязательно может попасться задача, связанная с условием Фано. Может просто быть задача на кодирование и декодирование информации.
Задача (Заключительная)
Для кодирования букв X, К, Л, О, Д решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ХОЛОДОК таким способом и результат запишите шестнадцатеричным кодом.
Решение:
Распишем, как кодируются все буквы в двоичной системе. Ноль и один кодируются одним разрядом, поэтому к ним слева приписывается ноль, как написано в условии.
| Буква | Десятичное Представление | Двоичное Представление |
| Х | 0 | 00 |
| К | 1 | 01 |
| Л | 2 | 10 |
| О | 3 | 11 |
| Д | 4 | 100 |
Выписываем слово ХОЛОДОК и под ним кодовые слова букв.
Чтобы перевести из двоичной системы число в шестнадцатиричную систему, мы должны двоичные цифры разбить по четвёркам, начиная с правого края. Каждая четвёрка превращается в цифру в шестандцатиричной системе. Таблицу перевода четвёрок двоичных цифр в шестнадцатиричную систему можно посмотреть в этой статье.
Т.к. ЕГЭ по информатике сдаётся в компьютерной форме, то можно воспользоваться стандартным калькулятором в режиме программист.
Ответ: 1DCD
На этом всё! Пусть Вам повезёт на ЕГЭ по информатике 2022.
В последней задаче буква К шифруется как 01, тогда почему в самом слове ХОЛОДОК она кодируется как 00?
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
Кодирование и декодирование информации
Кодирование
в различных системах счисления
№1. Для кодирования букв О, В, Д, П, А решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ВОДОПАД
таким способом и результат записать восьмеричным кодом, то получится
1) 22162
2) 1020342
3) 2131453
4) 34017
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
О |
В |
Д |
П |
А |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ВОДОПАД
— 010010001110010. Теперь разобьём это представление на тройки справа налево
и переведём полученный набор чисел в десятичный код, затем в восьмеричный
(восьмеричное предствление совпадает с десятичным при разбиении
тройками)
010 010 001 110 010 — 22162.
Правильный ответ указан под номером 1.
№2. Для кодирования букв Д, X, Р, О, В решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ХОРОВОД
таким способом и результат записать восьмеричным кодом, то получится
1) 12334
2) 2434541
3) 36714
4) 1323430
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
Д |
Х |
Р |
О |
В |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ХОРОВОД
— 011110111001100. Теперь разобьём это представление на тройки справа налево
и переведём полученный набор чисел в десятичный код, затем в восьмеричный
(восьмеричное предствление совпадает с десятичным при разбиении
тройками)
011 110 111 001 100 — 36714.
Правильный отвте указан под номером 3.
№3. Для кодирования букв О, К, Г, Д, Р решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ГОРОДОК
таким способом и результат записать восьмеричным кодом, то получится
1) 2040301
2) 16024
3) 1030402
4) 42061
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
О |
К |
Г |
Д |
Р |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ГОРОДОК
— 100010000110001. Теперь разобьём это представление на тройки справа налево
и переведём полученный набор чисел в десятичный код, затем в восьмеричный
(восьмеричное предствление совпадает с десятичным при разбиении
тройками)
100 010 000 110 001 — 42061.
Правильный отвте указан под номером 4.
№4. Для кодирования букв X, Е, Л, О, Д решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ЛЕДОХОД
таким способом и результат записать шестнадцатеричным кодом, то получится
1) 999С
2) 3254145
3) 123F
4) 2143034
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
Х |
Е |
Л |
О |
Д |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ЛЕДОХОД
— 1001100110011100. Теперь разобьём это представление на четвёрки справа
налево и переведём полученный набор чисел cначала в десятичный код,
затем в шестнадцатеричный.
1001 1001 1001 1100 — 9 9 9 12 — 999С.
Правильный ответ указан под номером 1.
№5. Для кодирования букв И, Д, Т, О, X решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ТИХОХОД
таким способом и результат записать шестнадцатеричным кодом, то получится
1) CD89
2) 89CD
3) 3154542
4) 2043431
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
И |
Д |
Т |
О |
Х |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ТИХОХОД
— 1000100111001101. Теперь разобьём это представление на четвёрки справа
налево и переведём полученный набор чисел cначала в десятичный код,
затем в шестнадцатеричный.
1000 1001 1100 1101 — 8 9 12 13 — 89СD.
Правильный ответ указан под номером 2.
№6. Для кодирования букв Р, С, Н, О, Г решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв НОСОРОГ
таким способом и результат записать восьмеричным кодом, то получится
1) 3424145
2) 2313034
3) 55634
4) 33100
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
Р |
С |
Н |
О |
Г |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: НОСОРОГ
— 101101110011100. Теперь разобьём это представление на тройки справа налево
и переведём полученный набор чисел в десятичный код (при представлении
двоичными тройками восьмеричный код совпадает с десятичным)
101 101 110 011 100 — 55634.
Правильный ответ указан под номером 3.
№7. Для кодирования букв Е, П, Н, Ч, Ь решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ПЕЧЕНЬЕ
таким способом и результат записать восьмеричным кодом, то получится
1) 1030240
2) 12017
3) 2141351
4) 23120
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
Е |
П |
Н |
Ч |
Ь |
|
0 |
1 |
2 |
3 |
4 |
|
000 |
001 |
010 |
011 |
100 |
Затем закодировать последовательность букв: ПЕЧЕНЬЕ
— 010011001010000. Теперь разобьём это представление на тройки справа налево
и переведём полученный набор чисел в десятичный код (при представлении
двоичными тройками восьмеричный код совпадает с десятичным)
010 011 001 010 000 — 23120.
Правильный ответ указан под номером 4.
№8. Для кодирования букв О, Ч, Б, А, К решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв КАБАЧОК
таким способом и результат записать шестнадцатеричным кодом, то получится
1) 5434215
2) 9DA4
3) ABCD
4) 4323104
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
О |
Ч |
Б |
А |
К |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: КАБАЧОК
— 1001110110100100. Теперь разобьём это представление на четвёрки справа
налево и переведём полученный набор чисел сначала в десятичный код,
затем в шестнадцатеричный:
1001 1101 1010 0100 — 9 13 10 4 — 9DA4.
Правильный ответ указан под номером 2.
№9. Для кодирования букв Р, И, К, П, А решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ПАПРИКА
таким способом и результат записать шестнадцатеричным кодом, то получится
1) Е634
2) А1В2
3) А45412А
4) 3430124
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
Р |
И |
К |
П |
А |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ПАПРИКА
— 1110011000110100. Теперь разобьём это представление на четвёрки справа
налево и переведём полученный набор чисел сначала в десятичный код,
затем в шестнадцатеричный:
1110 0110 0011 0100 — 14 6 3 4 — E634.
Правильный ответ указан под номером 1.
№10. Для кодирования букв О, Л, А, 3, К решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно
(с сохранением одного незначащего нуля в случае одноразрядного
представления). Если закодировать последовательность букв ЗАКОЛКА
таким способом и результат записать шестнадцатеричным кодом, то получится
1) 4351253
2) 9876
3) Е832
4) 3240143
Пояснение.
Сначала следует представить данные в условии числа в
двоичном коде:
|
О |
Л |
А |
З |
К |
|
0 |
1 |
2 |
3 |
4 |
|
00 |
01 |
10 |
11 |
100 |
Затем закодировать последовательность букв: ЗАКОЛКА
— 1110100000110010. Теперь разобьём это представление на четвёрки справа
налево и переведём полученный набор чисел сначала в десятичный код,
затем в шестнадцатеричный:
1110 1000 0011 0010 — 14 8 3 2 — E832.
Правильный ответ указан под номером 3.
Расшифровка сообщений
№1. Для 5 букв латинского алфавита заданы
их двоичные коды (для некоторых букв — из двух бит, для некоторых — из
трех). Эти коды представлены в таблице:
|
a |
b |
c |
d |
e |
|
000 |
110 |
01 |
001 |
10 |
Определите, какой набор букв закодирован двоичной
строкой 1100000100110
1) baade
2) badde
3) bacde
4) bacdb
Пояснение.
Мы видим, что выполняется условие Фано: никакое кодовое
слово не является началом другого кодового слова, поэтому однозначно
можем раскодировать сообщение с начала.
Разобьём код слева направо по данным таблицы и переведём
его в буквы:
110 000 01 001 10 — b a c d e.
Правильный ответ указан под номером 3.
№2. Для 5 букв латинского алфавита заданы их двоичные коды
(для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены
в таблице:
a b c d e
100 110 011 01 10
Определите, какой набор букв закодирован двоичной строкой
1000110110110, если известно, что все буквы в последовательности – разные:
1) cbade
2) acdeb
3) acbed
4) bacde
Пояснение.
Мы видим, что условия Фано и обратное условие Фано не выполняются,
значит код можно раскодировать неоднозначно.
Будем пробовать разные варианты, отбрасывая те, в которых получаются
повторяющиеся буквы:
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e
и b.
Такой вариант удовлетворет условию, значит, окончательно получили
ответ: acdeb.
Правильный ответ указан под номером 2.
№3. Для 6 букв латинского алфавита заданы
их двоичные коды (для некоторых букв из двух бит, для некоторых – из
трех). Эти коды представлены в таблице:
|
A |
B |
C |
D |
E |
F |
|
00 |
100 |
10 |
011 |
11 |
101 |
Определите, какая последовательность из 6 букв закодирована
двоичной строкой 011111000101100.
1) DEFBAC
2) ABDEFC
3) DECAFB
4) EFCABD
Пояснение.
Мы видим, что условия Фано и обратное условие Фано не выполняются,
значит код можно раскодировать неоднозначно.
Будем пробовать разные варианты, отбрасывая те, в
которых получаются повторяющиеся буквы:
1) 011 11 100 0101100
Первая буква определяется однозначно, её код 011: D.
Вторая буква также определится однозначно — E.
Пусть третья буква B, тогда следующая начинается с
кода 010, но таких букв в таблице нет, значит предположение не верно.
2) 011 11 10 00 101 100
Третья буква — С, потом — A. Мы хотим получить
ещё две буквы, чтобы в сумме их было 6, тогда следующая буква — F, и последняя
— B.
Окончательно получили ответ: DECAFB.
Правильный ответ указан под номером 3.
№4. Для кодирования сообщения, состоящего
только из букв О, К, Л, М и Б, используется неравномерный по длине двоичный
код:
|
О |
К |
Л |
М |
Б |
|
00 |
01 |
11 |
010 |
0110 |
Какое (только одно!) из четырех полученных сообщений
было передано без ошибок и может быть раскодировано:
1) 110001001001110
2) 10000011000111010
3) 110001001101001
4) 1000110001100010
Пояснение.
Разобьём каждый ответ на посимвольный код и найдём нужный
вариант:
Вариант 1: 11 00 010 01 00 11 10 — при таком разбиении
последняя часть кода не может быть раскодирована, а если разбить по-другому
11 00 01 00 10011, то сообщение также недекодируемо.
В вариантах 2 и 4 невозможно раскодировать начало
кода.
Вариант 3: 11 00 01 00 11 01 00 1 — при таком разбиении
последняя часть кода не может быть раскодирована. Разобьём по-другому:
11 00 01 00 11 010 01 — такой вариант разбиения может быть раскодирован.
.Правильный ответ указан под номером 3.
№5. Для передачи чисел по каналу с помехами
используется код проверки четности. Каждая его цифра записывается
в двоичном представлении, с добавлением ведущих нулей до длины 4, и
к получившейся последовательности дописывается сумма её элементов
по модулю 2 (например, если передаём 23, то получим последовательность
0010100110). Определите, какое число передавалось по каналу в виде
01100010100100100110?
1) 6543
2) 62926
3) 62612
4) 3456
Пояснение.
Из примера видно, что 2 знака кодируются 10 двоичными
разрядами (битами), на каждую цифру отводится 5 бит. В условии сказано,
что каждая цифра записывается кодом длиной 4 знака, значит, пятую цифру
можно откинуть.
Разобьём двоичную запись на группы по 5 знаков: 01100
01010 01001 00110. Отбрасываем послеюднюю цифру в каждой пятёрке и
первеодим в десятичную запись:
0110 0101 0100 0011 — 6 5 4 3.
Правильный ответ указан под номером 1.
№6. По каналу связи передаются сообщения,
содержащие только 5 букв А, И, К, О, Т. Для кодирования букв используется
неравномерный двоичный код с такими кодовыми словами:
А — 0, И — 00, К — 10, О — 110, Т — 111.
Среди приведённых ниже слов укажите такое, код которого
можно декодировать только одним способом. Если таких слов несколько,
укажите первое по алфавиту.
1) КАА
2) ИКОТА
3) КОТ
4) ни одно из сообщений не подходит
Пояснение.
Закодируем каждое слово.
КАА — 1000
ИКОТА — 00101110
КОТ — 10110111
Слово КАА можно декодировать как КИ
Слово ИКОТА можно декодировать как ААКОТА
Слово КОТ никак нельзя декодировать по-другому.
Следовательно, ответ 3.
№7. По каналу связи передаются сообщения,
содержащие только 5 букв А, И, К, О, Т. Для кодирования букв используется
неравномерный двоичный код с такими кодовыми словами:
А — 0, И — 00, К — 10, О — 110, Т — 111.
Среди приведённых ниже слов укажите такое, код которого
можно декодировать только одним способом. Если таких слов несколько,
укажите первое по алфавиту.
1) КИОТ
2) КООТ
3) ТААК
4) ни одно из сообщений не подходит
Пояснение.
Закодируем каждое слово.
КИОТ — 1000110111
КООТ — 10110110111
ТААК — 1110010
Слово КИОТ можно декодировать как КAA…
Слово ТААК можно декодировать как TИ…
Слово КООТ никак нельзя декодировать по другому.
Следовательно, ответ 2.
№8. По каналу связи передаются сообщения,
содержащие только 4 буквы — П, О, Р, Т. Для кодирования букв используются
5-битовые кодовые слова:
П — 11111, О — 11000, Р — 00100, Т — 00011.
Для этого набора кодовых слов выполнено такое свойство: любые
два слова из набора отличаются не менее чем в трёх позициях.
Это свойство важно для расшифровки сообщений при наличии
помех (в предположении, что передаваемые биты могут искажаться, но
не пропадают). Закодированное сообщение считается принятым корректно,
если его длина кратна 5 и каждая пятёрка отличается от некоторого кодового
слова не более чем в одной позиции; при этом считается, что пятёрка кодирует
соответствующую букву. Например, если принята пятерка 00000, то считается,
что передавалась буква Р.
Среди приведённых ниже сообщений найдите то, которое
принято корректно, и укажите его расшифровку (пробелы несущественны).
11011 11100 00011 11000 01110
00111 11100 11110 11000 00000
1) ПОТОП
2) РОТОР
3) ТОПОР
4) ни одно из сообщений не принято корректно
Пояснение.
Длина обоих сообщений кратна пяти.
Анализируя первое сообщение «11011 11100 00011
11000 01110», приходим к выводу, что оно принято некорректно, поскольку
нет такого слова, которое бы отличалось от слова «01110» только
в одной позиции.
Рассмотрим второе сообщение. Учитывая, что каждая
пятёрка отличается от некоторого кодового слова не более чем в одной
позиции, его возможно расшифровать только как «ТОПОР».
№9. По каналу связи передаются сообщения,
содержащие только 4 буквы — П, О, Р, Т. Для кодирования букв используются
5-битовые кодовые слова:
П — 00000, О — 00111, Р — 11011, Т — 11100.
Для этого набора кодовых слов выполнено такое свойство: любые
два слова из набора отличаются не менее чем в трёх позициях.
Это свойство важно для расшифровки сообщений при наличии
помех (в предположении, что передаваемые биты могут искажаться, но
не пропадают). Закодированное сообщение считается принятым корректно,
если его длина кратна 5 и каждая пятёрка отличается от некоторого кодового
слова не более чем в одной позиции; при этом считается, что пятёрка кодирует
соответствующую букву. Например, если принята пятерка 11111, то считается,
что передавалась буква Р.
Среди приведённых ниже сообщений найдите то, которое
принято корректно, и укажите его расшифровку (пробелы несущественны).
11011 10111 11101 00111 10001
10000 10111 11101 00111 00001
1) ПОТОП
2) РОТОР
3) ТОПОР
4) ни одно из сообщений не принято корректно
Пояснение.
Длина обоих сообщений кратна пяти.
Анализируя первое сообщение «11011 10111 11101
00111 10001», приходим к выводу, что оно принято некорректно, поскольку
нет такого слова, которое бы отличалось от слова «10001» только
в одной позиции.
Рассмотрим второе сообщение. Учитывая, что каждая
пятёрка отличается от некоторого кодового слова не более чем в одной
позиции, его возможно расшифровать только как «ПОТОП».
№10. По каналу связи передаются сообщения,
содержащие только 4 буквы — П, О, Р, Т. Для кодирования букв используются
5-битовые кодовые слова:
П — 00000, О — 00111, Р — 11011, Т — 11100.
Для этого набора кодовых слов выполнено такое свойство: любые
два слова из набора отличаются не менее чем в трёх позициях.
Это свойство важно для расшифровки сообщений при наличии
помех (в предположении, что передаваемые биты могут искажаться, но
не пропадают). Закодированное сообщение считается принятым корректно,
если его длина кратна 5 и каждая пятёрка отличается от некоторого кодового
слова не более чем в одной позиции; при этом считается, что пятёрка кодирует
соответствующую букву. Например, если принята пятерка 11111, то считается,
что передавалась буква Р.
Среди приведённых ниже сообщений найдите то, которое
принято корректно, и укажите его расшифровку (пробелы несущественны).
11011 10111 11101 00111 10001
10000 10111 11101 00111 00001
1) ПОТОП
2) РОТОР
3) ТОПОР
4) ни одно из сообщений не принято корректно
Пояснение.
Длина обоих сообщений кратна пяти.
Анализируя первое сообщение «11011 10111 11101
00111 10001», приходим к выводу, что оно принято некорректно, поскольку
нет такого слова, которое бы отличалось от слова «10001» только
в одной позиции.
Рассмотрим второе сообщение. Учитывая, что каждая
пятёрка отличается от некоторого кодового слова не более чем в одной
позиции, его возможно расшифровать только как «ПОТОП».
№11. Для передачи данных по каналу связи
используется 5-битовый код. Сообщение содержит только буквы А, Б и
В, которые кодируются следующими кодовыми словами:
А — 11010, Б — 00110, В — 10101.
При передаче возможны помехи. Однако некоторые
ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов
отличаются друг от друга не менее чем в трёх позициях. Поэтому если
при передаче слова произошла ошибка не более чем в одной позиции, то
можно сделать обоснованное предположение о том, какая буква передавалась.
(Говорят, что «код исправляет одну ошибку».) Например, если получено
кодовое слово 10110, считается, что передавалась буква Б. (Отличие
от кодового слова для Б только в одной позиции, для остальных кодовых
слов отличий больше.) Если принятое кодовое слово отличается от кодовых
слов для букв А, Б, В более чем в одной позиции, то считается, что произошла
ошибка (она обозначается ‘х’).
Получено сообщение 00111 11110 11000 10111. Декодируйте
это сообщение — выберите правильный вариант.
1) БААх
2) БААВ
3) хААх
4) хххх
Пояснение.
Декодируем каждое слово сообщения. Первое слово:
00111 отличается от буквы Б только одной позицией. Второе слово: 11110
отличается от буквы А только одной позицией. Третье слово: 11000 отличается
от буквы А только одной позицией. Четвёртое слово: 10111 отличается от
буквы В только одной позицией.
Таким образом, ответ: БААВ.
Передача информации и выбор кода
№1. Для передачи по каналу связи сообщения,
состоящего только из букв А, Б, В, Г, решили использовать неравномерный
по длине код: A=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина
кода была минимальной и допускалось однозначное разбиение кодированного
сообщения на буквы?
1) 0001
2) 000
3) 11
4) 101
Пояснение.
Для того, чтобы сообщение, записанное с помощью неравномерного
по длине кода, однозначно раскодировалось, требуется, чтобы никакой
код не был началом другого (более длинного) кода.
Рассмотрим варианты для буквы Г, начиная с самого
короткого.
3) Г=11: код буквы A является началом этого кода, поэтому
этот вариант не подходит.
4) Код Г=101 не подходит по аналогичной причине.
2) Код Г=000 не сопадает с началом ни одного кода,следовательно
это и есть правильный ответ.
Правильный ответ указан под номером 2.
№2. Для передачи по каналу связи сообщения,
состоящего только из букв А, Б, В, Г, решили использовать неравномерный
по длине код: A=0, Б=100, В=101. Как нужно закодировать букву Г, чтобы
длина кода была минимальной и допускалось однозначное разбиение кодированного
сообщения на буквы?
1) 1
2) 11
3) 01
4) 010
Пояснение.
Для того, чтобы сообщение, записанное с помощью неравномерного
по длине кода, однозначно раскодировалось, требуется, чтобы никакой
код не был началом другого (более длинного) кода.
Рассмотрим варианты для буквы Г, начиная с самого
короткого.
1) Г=1: код буквы Г является началом кода буквы В=101 и
Б=100, поэтому этот вариант не подходит.
2) Код Г=11 не сопадает с началом ни одного кода,следовательно
это и есть правильный ответ.
В вариантах 3) и 4) код буквы А=0 является началом
кода буквы Г, поэтому они не подходят.
№3. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный
код, позволяющий однозначно декодировать полученную двоичную последовательность.
Вот этот код: А–10, Б–001, В–0001, Г–110, Д–111.
Можно ли сократить для одной из букв длину кодового
слова так, чтобы код по-прежнему можно было декодировать однозначно?
Коды остальных букв меняться не должны. Выберите правильный вариант
ответа.
1) это невозможно
2) для буквы В – 000
3) для буквы Б – 0
4) для буквы Г – 11
Пояснение.
Мы видим, что выполняется условие Фано: никакое кодовое
слово не является началом другого кодового слова, поэтому однозначно
можем раскодировать сообщение с начала.
Чтобы сократить код одной буквы, необходимо выполнение
условия Фано в новом коде.
Вариант 3 не подходит, потому что 0 является началом
кода 0001.
Вариант 4 не подходит, потому что код 1 является началом
кода 111.
Вариант 2 подходит, так как не нарушает условия
Фано.
Правильный ответ указан под номером 2.
№4. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный
код, позволяющий однозначно декодировать полученную двоичную последовательность.
Вот этот код: А–011, Б–000, В–11, Г–001, Д–10. Можно ли сократить для одной
из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать
однозначно? Коды остальных букв меняться не должны. Выберите правильный
вариант ответа.
1) это невозможно
2) для буквы А – 01
3) для буквы Б – 00
4) для буквы Г – 00
Пояснение.
Мы видим, что выполняется условие Фано: никакое кодовое
слово не является началом другого кодового слова, поэтому однозначно
можем раскодировать сообщение с начала.
Чтобы сократить код одной буквы, необходимо выполнение
условия Фано в новом коде.
Вариант 3 не подходит, потому что 00 является началом
кода 001.
Вариант 4 не подходит, потому что код 00 является
началом кода 000.
Вариант 2 подходит, так как не нарушает условия
Фано.
Правильный ответ указан под номером 2.
№5. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный
код, позволяющий однозначно декодировать полученную двоичную последовательность.
Вот этот код: А – 00, Б – 01, В – 100, Г – 101, Д – 110. Можно ли сократить
для одной из букв длину кодового слова так, чтобы код по-прежнему можно
было декодировать однозначно? Коды остальных букв меняться не должны.
Выберите правильный вариант ответа.
1) для буквы Д – 11
2) это невозможно
3) для буквы Г – 10
4) для буквы Д – 10
Пояснение.
Мы видим, что выполняется условие Фано: никакое кодовое
слово не является началом другого кодового слова, поэтому однозначно
можем раскодировать сообщение с начала.
Чтобы сократить код одной буквы, необходимо выполнение
условия Фано в новом коде.
Вариант 3 не подходит, потому что 10 является началом
кода 100.
Вариант 4 не подходит, потому что код 10 является
началом кода 100 и 101.
Вариант 1 подходит, так как не нарушает условия
Фано.
Правильный ответ указан под номером 1.
№6. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный
двоичный код, позволяющий однозначно декодировать двоичную последовательность,
появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г
использовали такие кодовые слова: А–111, Б–110, В–100, Г–101.
Укажите, каким кодовым словом может быть закодирована
буква Д. Код должен удовлетворять свойству однозначного декодирования.
Если можно использовать более одного кодового слова, укажите кратчайшее
из них.
1) 0
2) 01
3) 00
4) 000
Пояснение.
Мы видим, что выполняется условие Фано: никакое кодовое
слово не является началом другого кодового слова, поэтому однозначно
можем раскодировать сообщение с начала.
Чтобы закодировать Д, необходимо выполнение условия
Фано в новом коде.
Каждый из этих вариантов может быть новым словом, т. к.
не является началом ни одного из кодовых слов. Поэтому выбираем
самое короткое — 0.
Правильный ответ указан под номером 1.
№7. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный
двоичный код, позволяющий однозначно декодировать двоичную последовательность,
появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г
использовали такие кодовые слова: А — 100, Б — 101, В — 111, Г — 110.
Укажите, каким кодовым словом из перечисленных ниже
может быть закодирована буква Д. Код должен удовлетворять свойству однозначного
декодирования. Если можно использовать более одного кодового
слова, укажите кратчайшее из них.
1) 000
2) 10
3) 11
4) 1111
Пояснение.
Для того, чтобы сообщение, записанное с помощью неравномерного
по длине кода, однозначно раскодировалось, требуется, чтобы никакой
код не был началом другого (более длинного) кода.
Рассмотрим варианты для буквы Д, начиная с самого
короткого.
1) Д=10: код буквы Д является началом кода буквы Б=101,
поэтому этот вариант не подходит.
2) Д=11: код буквы Д является началом кода буквы В=111,
Д=110, поэтому этот вариант не подходит.
3) Д=000: код буквы Д не является началом другого
кода, следовательно, это правильный ответ.
4) Д=1111: код буквы Д является началом кода буквы
В=111, поэтому этот вариант не подходит.
Правильный ответ указан под номером 1.
№8. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный
двоичный код, позволяющий однозначно декодировать двоичную последовательность,
появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г
использовали такие кодовые слова: А — 001, Б — 010,
В— 000, Г — 011.
Укажите, каким кодовым словом из перечисленных ниже
может быть закодирована буква Д.
Код должен удовлетворять свойству однозначного декодирования.
Если можно использовать более одного кодового слова, укажите кратчайшее
из них.
1) 00
2) 01
3) 101
4) 0000
Пояснение.
Для того, чтобы сообщение, записанное с помощью неравномерного
по длине кода, однозначно раскодировалось, требуется, чтобы никакой
код не был началом другого (более длинного) кода.
Рассмотрим варианты для буквы Д, начиная с самого
короткого.
1) Д=00: код буквы Д является началом кода буквы В=000,
поэтому этот вариант не подходит.
2) Д=01: код буквы Д является началом кода буквы Б=010,
Г=011, поэтому этот вариант не подходит.
3) Д=101: код буквы Д не является началом другого
кода, следовательно, это правильный ответ.
Правильный ответ указан под номером 3.
№9. Для кодирования некоторой последовательности,
состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный
двоичный код, позволяющий однозначно декодировать двоичную последовательность,
появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г
использовали такие кодовые слова: А — 111, Б — 110, В — 101,
Г — 100.
Укажите, каким кодовым словом из перечисленных ниже
может быть закодирована буква Д. Код должен удовлетворять свойству однозначного
декодирования. Если можно использовать более одного кодового
слова, укажите кратчайшее из них.
1) 1
2) 0
3) 01
4) 10
Пояснение.
Для того, чтобы сообщение, записанное с помощью неравномерного
по длине кода, однозначно раскодировалось, требуется, чтобы никакой
код не был началом другого (более длинного) кода. Рассмотрим варианты
для буквы Д, начиная с самого короткого.
1) Д=1: код буквы Д является началом всех представленных
кодов букв, поэтому этот вариант не подходит.
2) Д=0: код буквы Д не является началом другого кода,
поэтому этот вариант подходит.
3) Д=01: код буквы Д не является началом другого
кода, поэтому этот вариант подходит.
4) Д=10: код буквы Д является началом кодов букв В и Г,
следовательно, этот вариант не подходит.
Таким образом, подходят два варианта: 0 и 01. 0 короче,
чем 01.
Правильный ответ указан под номером 2.
№10. По каналу связи передаются сообщения,
содержащие только 4 буквы: E, H, O, T. Для кодирования букв E, H, O используются
5-битовые кодовые слова: E — 00000, H — 00111, O — 11011.
Для этого набора кодовых слов выполнено такое свойство: любые
два слова из набора отличаются не менее чем в трех позициях.
Это свойство важно для расшифровки сообщений при наличии
помех. Какое из перечисленных ниже кодовых слов можно использовать для
буквы T, чтобы указанное свойство выполнялось для всех четырёх кодовых
слов?
1) 11111
2) 11100
3) 00011
4) не подходт ни одно из указанных выше слов
Пояснение.
Пользуясь правилом «любые два слова из набора отличаются
не менее чем в трех позициях» проверим все возможные варианты.
Число 11111 отличается от кодового слова 00111 только
в двух позициях.
Число 11100 отличается от кодового слова 00000 — в
трех позициях, от 00111 — в четырех позициях, 11011 — в трех позициях.
Правильный вариант ответа второй.
В соответствии с контрольно-измерительными
материалами ЕГЭ по информатике и ИКТ (http://www.fipi.ru/)
проверка умений и знаний, связанных с
кодированием информации и определением
информационного объема сообщений,
осуществляется в следующих заданиях ЕГЭ:
Задание 1. Умение кодировать и
декодировать информацию (базовый уровень
сложности).
Задание 4. Знания о системах счисления
и двоичном представлении информации в памяти
компьютера (базовый уровень сложности).
Задание 9. Умение определять скорость
передачи информации при заданной пропускной
способности канала (базовый уровень сложности).
Задание 10. Анализ
последовательностей, системы счисления (базовый
уровень сложности).
Задание 13. Умение подсчитывать
информационный объем сообщения (повышенный
уровень сложности).
Задание 16. Знание позиционных систем
счисления (повышенный уровень сложности).
Рассмотрим, что же необходимо знать учащимся
для выполнения вышеперечисленных заданий ЕГЭ и
познакомимся с некоторыми способами решения
различных типов задач, связанных с кодированием
и декодированием информации различного вида, а
также с определением информационного объема
сообщений.
Задание 4. Знания о системах счисления и
двоичном представлении информации в памяти
компьютера
Числовая информация кодируется с помощью
систем счисления.
Учащимся необходимо знать:
- Правила перевода чисел из 10-ной системы
счисления в другие позиционные системы
счисления и обратно. - Правила перевода чисел из двоичной системы
счисления в 8-ую и 16-ую и обратно. - Разрядные сетки для представления целых
неотрицательных чисел и целых чисел со знаком
(слайд 6 Приложение). - Отрицательные целые числа хранятся в памяти
компьютера в дополнительном коде.
Для получения дополнительного кода
отрицательного числа нужно сделать следующие
операции:
— перевести число в двоичную систему счисления;
— записать прямой код полученного двоичного
числа;
— записать обратный код, сделав инверсию всех
битов, кроме знакового разряда;
— к полученному обратному коду прибавить
единицу.
Рассмотрим решения задач 1 – 7, приведенные на
слайдах 8 – 14 (Приложение).
На слайдах 15, 16 приведен оптимальный набор
тренировочных задач для задания 4 ЕГЭ.
Задание 1. Умение кодировать и декодировать
информацию
Кодирование – это перевод информации с одного
языка на другой язык, с помощью другого алфавита.
Кодирование может быть равномерным и
неравномерным. При равномерном кодировании все
символы кодируются кодами равной длины. При
неравномерном кодировании разные символы могут
кодироваться кодами разной длины.
Учащимся необходимо знать:
- Закодированное сообщение можно однозначно
декодировать с начала, если выполняется условие
Фано: никакое кодовое слово не является началом
другого кодового слова. - Закодированное сообщение можно однозначно
декодировать с конца, если выполняется обратное
условие Фано: никакое кодовое слово не является
окончанием другого кодового слова.
Условие Фано – это достаточное, но не
необходимое условие однозначного декодирования.
Рассмотрим решения задач 1 – 6, приведенные на
слайдах 19 – 25 (Приложение).
На слайдах 26 — 29 приведен оптимальный набор
тренировочных задач для задания 1 ЕГЭ.
Задание 13. Кодирование текстовой информации.
Кодировка ASCII. Основные кодировки кириллицы
Согласно алфавитному подходу к измерению
количества информации все символы кодируются
одинаковым числом бит. Чаще всего используют
кодировки, в которых на символ отводится 8 бит или
16 бит. При кодировании текста каждому символу
ставится в соответствие свой код.
Учащимся необходимо знать:
- Единицы измерения количества информации и
соотношения между этими единицами (слайд 31 Приложение). - Степени числа 2 и правила выполнения
арифметических операций над числами со
степенями (слайд 32 Приложение). - Символы-цифры в кодовой таблице идут подряд в
порядке возрастания, от “0” до “9”. - Прописные латинские буквы в кодовой таблице
идут подряд в алфавитном порядке от “A” до “Z”. - Строчные латинские буквы в таблице кодировки
идут подряд в алфавитном порядке, от “a” до “z”.
В большинстве кодовых таблиц русские буквы, как
прописные, так и строчные, также расположены по
алфавиту (за исключением буквы “Ё”).
Чтобы найти информационный объем текста (IT),
нужно умножить количество символов в тексте (k) на
число бит, которые отводятся на один символ (I).
IT = k • I
Число бит, которые отводятся на один символ (I),
вычисляется из формулы:
N = 2I ,
где N – количество символов в алфавите.
Рассмотрим решения задач 1 – 6, приведенные на
слайдах 34 – 39 (Приложение).
На слайдах 40 — 42 приведен оптимальный набор
тренировочных задач на кодирование текстовой
информации.
Задание 10. Анализ последовательностей, системы
счисления
Учащимся необходимо знать:
- Правила перевода чисел из 10-ной системы
счисления в другие позиционные системы
счисления. - Правила перевода чисел в 10-ую систему
счисления из других позиционных систем
счисления.
Формулу вычисления количества различных
последовательностей:
N = SI ,
где N – количество различных
последовательностей,
S – количество различных символов используемых
в последовательности,
I – длина последовательности (количество
символов в последовательности).
Рассмотрим решения задач 1 – 4, приведенные на
слайдах 44 – 48 (Приложение).
На слайдах 49 — 51 приведен оптимальный набор
тренировочных задач для задания 10 ЕГЭ.
Задание 13. Умение подсчитывать информационный
объем сообщения
Учащимся необходимо знать:
- Если алфавит имеет мощность M, то количество
возможных символьных цепочек длиной I равно N = M I - Для двоичного кодирования получаем формулу: N =
2 I
C помощью I бит можно закодировать N = 2 I
различных вариантов (чисел).
Чтобы найти информационный объем текста (IT),
нужно умножить количество символов в тексте (k) на
число бит, которые отводятся на один символ (I):
IT = k • I
Число бит, которые отводятся на один символ (I),
вычисляется из формулы: N = 2 I ,
где N – количество символов в алфавите.
По формуле Шеннона количество информации в
сообщении о произошедшем событии с номером i
равно
Ii = — log2 Pi ,
где Pi – вероятность этого события.
Рассмотрим решения задач 1 – 8, приведенные на
слайдах 54 – 61 (Приложение).
На слайдах 62 — 64 приведен оптимальный набор
тренировочных задач для задания 13 ЕГЭ.
Задание 16. Знание позиционных систем счисления
Учащимся необходимо знать:
- Принципы кодирования чисел в позиционных
системах счисления.
Чтобы перевести число из системы счисления с
основанием N в десятичную систему, нужно умножить
значение каждой цифры числа на N в степени, равной
ее разряду. Например,
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2
+ 4·N1 + 5·N0
Последняя цифра записи числа в системе
счисления с основанием N – это остаток от деления
этого числа на N.
Две последние цифры – это остаток от деления
числа на N 2, и т.д.
Число 2N в двоичной системе записывается
как единица и N нулей.
Число 2N-1 в двоичной системе записывается
как N единиц.
Число 2N–2K при K < N в двоичной
системе счисления записывается как N–K единиц и K
нулей.
Рассмотрим решения задач 1 – 4, приведенные на
слайдах 67 – 70 (Приложение).
На слайдах 71 — 72 приведен оптимальный набор
тренировочных задач для задания 16 ЕГЭ.
Задание 9. Скорость передачи информации при
заданной пропускной способности канала
Обмен информацией производится по каналам
передачи информации.
Учащимся необходимо знать:
- Основной характеристикой каналов передачи
информации является их пропускная способность
(скорость передачи информации). - Пропускная способность канала равна количеству
информации, которое может передаваться по нему в
единицу времени. - Пропускная способность измеряется в бит/с,
байт/c, Кбит/c, Кбайт/c, и т.д. - Объем переданной информации вычисляется по
формуле
I = v • t
где v – пропускная способность канала (в битах в
секунду или подобных единицах), t – время
передачи.
Рассмотрим решения задач 1 – 3, приведенные на
слайдах 75 – 79 (Приложение).
На слайдах 80 — 81 приведен оптимальный набор
тренировочных задач для задания 9 ЕГЭ.
Источники заданий:
1) Демонстрационные варианты ЕГЭ 2009-2015 гг. http://www.fipi.ru
2) Е.М. Островская, Н.Н. Самылкина ЕГЭ 2012.
Информатика. Сдаем без проблем! — М.: Эксмо, 2011.
3) Крылов С.С., Лещинер В.Р., Якушкин П.А. ЕГЭ 2010.
Информатика. Универсальные материалы для
подготовки учащихся. — Интеллект-Центр, 2010.
4) Тренировочные и диагностические работы МИОО
2010-2015 гг. http://www.mioo.ru
5) Задания для тренировки с сайта К. Полякова
http://kpolyakov.spb.ru