Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Всего: 11 1–11
Добавить в вариант
В кубе ABCDA1B1C1D1 точка O1 — центр квадрата ABCD, точка O2 — центр квадрата CC1D1D.
а) Докажите, что прямые A1O1 и B1O2 скрещиваются.
б) Найдите расстояние между прямыми A1O1 и B1O2 , если ребро куба равно 1.
Источник: А. Ларин. Тренировочный вариант № 294.
Источник: А. Ларин: Тренировочный вариант № 9.
В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD с диагоналями AC = 8 и BD = 6.
а) Докажите, что прямые BD1 и AC перпендикулярны.
б) Найдите расстояние между прямыми BD1 и AC, если известно, что боковое ребро призмы равно 12.
Источник: А. Ларин: Тренировочный вариант № 124.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 AB = 2, AA1 = 3.
а) Докажите, что прямые AC1 и BE перпендикулярны.
б) Найдите расстояние между прямыми AC1 и BE.
Источник: А. Ларин: Тренировочный вариант № 118.
В кубе ребро которого равно 6, точки M и N — середины ребер AB и
соответственно, а точка K расположена на ребре DC так, что
а) Найдите расстояние между прямыми MN и AK.
б) Расстояние от точки до плоскости треугольника MNK.
Источник: А. Ларин: Тренировочный вариант № 253.
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
а) Докажите, что AA1 = AC.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 6, BC = 3.
Источник: Задания 14 (C2) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 401 (C часть).
В кубе ABCDA1B1C1D1 точка О1 — центр квадрата АВСD, точка О2 — центр квадрата СС1D1D.
а) Докажите, что прямые А1О1 и В1О2 — скрещивающиеся.
б) Найдите расстояние между прямыми А1О1 и В1О2, если ребро куба равно 2.
Источник: А. Ларин: Тренировочный вариант № 220.
Основание прямой четырёхугольной призмы ABCDA1B1C1D1 — прямоугольник ABCD, в котором
Расстояние между прямыми AC и B1D1 равно 5.
а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой BD1, делит отрезок BD1 в отношении 1 : 7, считая от вершины D1.
б) Найдите косинус угла между плоскостью, проходящей через точку D перпендикулярно прямой BD1, и плоскостью основания призмы.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 6. (Часть C).
В правильной четырехугольной пирамиде SABCD точка P — середина ребра SA, точка Q — середина ребра SC.
а) Докажите, что расстояние между прямыми BP и DQ не зависит от высоты пирамиды.
б) Найдите это расстояние, если площадь основания пирамиды равна 5.
Источник: А. Ларин. Тренировочный вариант № 269.
Раздел: Правильная четырёхугольная пирамида
Источник: А. Ларин: Тренировочный вариант № 12.
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Прямые CA1 и AB1 перпендикулярны.
а) Докажите, что AA1 = AС.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 7, BC = 8.
Источник: Задания 14 (C2) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
Всего: 11 1–11
Расстояние между двумя прямыми. Метод координат. Задание 14
В этой статье я хочу показать решение задачи на нахождение расстояния между скрещивающимися прямыми, которую мы уже решали геометрическим способом, но теперь с помощью метода координат. Я специально показываю решение одной задачи разными способами, чтобы у вас была возможность выбрать наиболее удобный для вас.
Итак, аналитический способ решения задачи:
В правильной треугольной призме 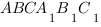

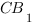
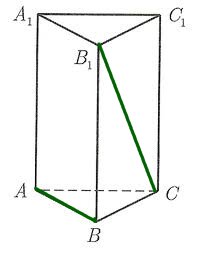

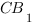
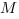

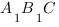
Рассстояние 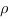
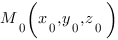

Поместим нашу призму в систему координат. Если мы решаем задачу с кубом или прямоугольным параллелепипедом, то выбор системы координат очевиден: мы помещаем начало координат в одну из вершин куба, а оси направляем вдоль ребер. В случае призмы это не столь очевидно.
Нам надо выбрать систему координат таким образом, чтобы координаты точки 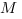
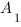
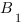
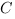
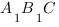
Запишем координаты нужных нам точек:
Чтобы найти коэффициенты 

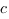
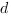

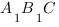
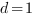
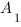
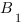
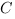
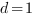
Получим систему уравнений:
Отсюда:
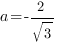
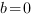
Подставим значения коэффициентов и координаты точки 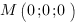
Ответ:
И.В. Фельдман, репетитор по математике.
Расстояние между двумя скрещивающимися прямыми
Воскресенье, 25 ноября, 2012
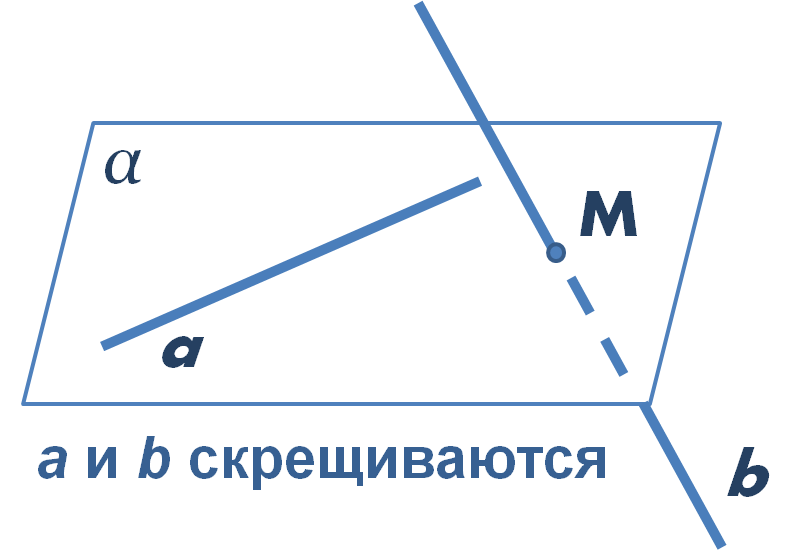
В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения расстояния между скрещивающимися прямыми с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).
Для нахождения расстояния между скрещивающимися прямыми необходимо:
- Провести через одну из скрещивающихся прямых плоскость, которая параллельна другой скрещивающейся прямой.
- Опустить перпендикуляр из любой точки второй прямой на полученную плоскость. Длина этого перпендикуляра будет являться искомым расстоянием между прямыми.
Разберем данный алгоритм подробнее на примере решения задачи C2 из ЕГЭ по математике.
Расстояние между прямыми в пространстве
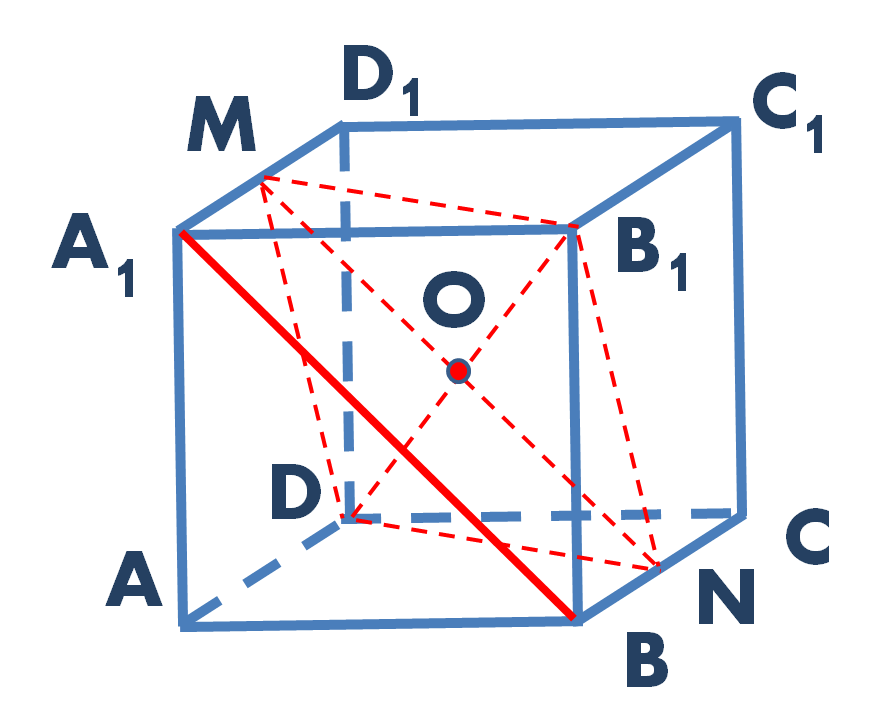
Задача. В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми BA1 и DB1.
Рис. 1. Чертеж к задаче
Решение. Через середину диагонали куба DB1 (точку O) проведем прямую, параллельную прямой A1B. Точки пересечения данной прямой с ребрами BC и A1D1 обозначаем соответственно N и M. Прямая MN лежит в плоскости MNB1 и параллельна прямой A1B, которая в этой плоскости не лежит. Это означает, что прямая A1B параллельна плоскости MNB1 по признаку параллельности прямой и плоскости (рис. 2).
Рис. 2. Искомое расстояние между скрещивающимися прямыми равно расстоянию от любой точки выделенной прямой до изображенной плоскости
Ищем теперь расстояние от какой-нибудь точки прямой A1B до плоскости MNB1. Это расстояние по определению будет являться искомым расстоянием между скрещивающимися прямыми.
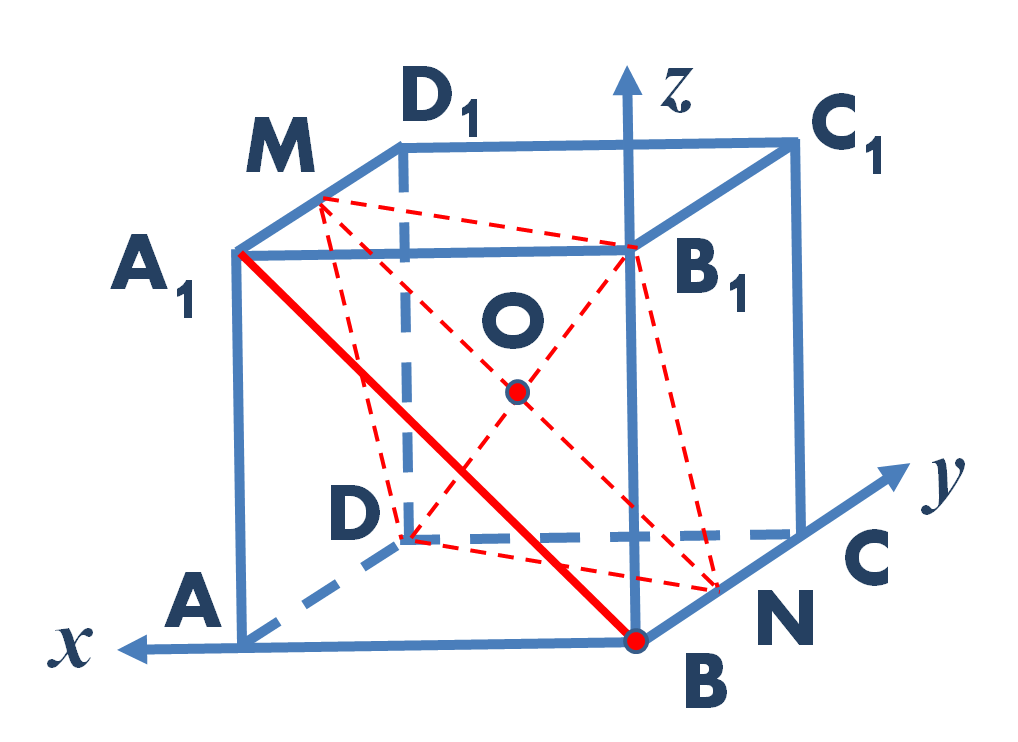
Для нахождения этого расстояния воспользуемся методом координат. Введем прямоугольную декартову систему координат таким образом, чтобы ее начало совпало с точкой B, ось X была направлена вдоль ребра BA, ось Y — вдоль ребра BC, ось Z — вдоль ребра BB1 (рис. 3).
Рис. 3. Прямоугольную декартову систему координат выберем так, как показано на рисунке
Находим уравнение плоскости MNB1 в данной системе координат. Для этого определяем сперва координаты точек M, N и B1:
Полученные координаты подставляем в общее уравнение прямой
и получаем следующую систему уравнений:
Из второго уравнения системы получаем из третьего получаем
после чего из первого получаем
Подставляем полученные значения в общее уравнение прямой:
Замечаем, что иначе плоскость MNB1 проходила бы через начало координат. Делим обе части этого уравнения на
и получаем:
Расстояние от точки до плоскости определяется по формуле:
где — координаты точки B.
— коэффициенты при переменных
в уравнении плоскости. Точка B имеет координаты
Получаем окончательно:
Ответ:
Сергей Валерьевич
Репетитор по геометрии в Тропарёво
Слайд 1
Методы нахождения расстояний между скрещивающимися прямыми. Автор : Сигодина Лариса Владимировна, учитель математики МБОУ «БСОШ №1 им. П. П. Корягина » Благовещенского района Алтайского края 2016
Слайд 2
Методы нахождения расстояний между скрещивающимися прямыми. Определение 1: Расстоянием между скрещивающимися прямыми называется расстояние между ближайшими точками этих прямых. Определение2: Расстояние между скрещивающимися прямыми называется длина их общего перпендикуляра. Определение 3: … называется расстояние между их проекциями на плоскость, перпендикулярную одной из этих прямых. Определение 4: …называется расстояние от одной из скрещивающихся прямых до параллельной плоскости, проходящей через другую прямую. Определение 5:… называется расстояние между параллельными плоскостями, в которых находятся скрещивающиеся прямые.
Слайд 3
Опр2: Расстояние между скрещивающимися прямыми называется длина их общего перпендикуляра. 1. ( BB 1 ; DC 1 ) BC a 2. ( AA 1 ; DC ) AD a 3 . ( DC ; A 1 K ) DD 1 a A B 1 A 1 C B D D 1 C 1 К
Слайд 4
Опр 3: Расстоянием между скрещивающимися прямыми называется расстояние между их проекциями на плоскость, перпендикулярную одной из этих прямых. Построим плоскость, перпендикулярную прямой a Проекция прямой а на плоскость – точка А Проекция прямой b на эту плоскость – прямая b 1 4 . ( a ; b ) ( A ; b 1 ) Метод ортогонального проектирования
Слайд 5
Опр 3: Расстоянием между скрещивающимися прямыми называется расстояние между их проекциями на плоскость, перпендикулярную одной из этих прямых. ( B 1 D ; AC ) OK A B 1 A 1 C B D D 1 C 1 H O K 2) Проекция АС – О 3) Проекция В 1 D – В 1 D 4) OK B 1 D
Слайд 6
4 В правильной треугольной пирамиде сторона основания равна 4, а боковое ребро 3. Найдите расстояние от стороны основания до противоположного бокового ребра. D B A C 3 4 3 Построим плоскость, перпендикулярную прямой АС. N Спроектируем на плоскость BDN обе прямые. Проекция А C – точка N , а проекция BD — BD NK – искомое расстояние. Кстати в этой задаче получился именно общий перпендикуляр . 4 3 K
Слайд 7
D B A C 3 4 3 4 N 4 K 3 2 3 2 5 N D 3 2 К В 5 3 h x 3-x «–» Подставим во второе уравнение
Слайд 8
Опр 4: Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до параллельной плоскости, проходящей через другую прямую. A B 1 A 1 C B D D 1 C 1 ( A K ; B C ) CO К О Проведем плоскость ADB 1 , в которой лежит прямая AK BC ║ AD, BC║ADB 1
Слайд 9
Опр 4: Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до параллельной плоскости, проходящей через другую прямую. A B 1 A 1 C B D D 1 C 1 ( DD 1 ; A K ) D 1 O К О H
Слайд 10
Опр 5: Расстоянием между скрещивающимися прямыми называется расстояние между параллельными плоскостями, в которых находятся скрещивающиеся прямые. A B 1 A 1 C B D D 1 C 1 O
Слайд 11
B 1 D D 1 С 1 1 O H
Слайд 12
Метод координат Расстояние от точки до плоскости Вычисляется по формуле: Ввести «удобным» способом систему координат. Найти координаты «нужных» точек. Записать уравнение плоскости. Вычислить расстояние по формуле.
Слайд 13
A B 1 A 1 C B D D 1 C 1 O x z y Найдем расстояние от точки D до плоскости В 1 С D 1 D(0,0,0); C(0,1,0); D 1 (0,0,1); B 1 (1,1,1) 0+1b+0+d=0; 0+0+1c+d=0; 1a+1b+1c+d=0 d=1 b=-1; c=-1; a=1; Уравнение плоскости В 1 С D 1 x-y-z+1=0
Слайд 14
A B C A 1 C 1 B 1 Правильная призма, все ребра равны 1. М К О
Слайд 15
A B C A 1 C 1 B 1 Правильная призма, все ребра равны 1. М y z x
Слайд 16
A B S D O C Дана правильная пирамида АВ= 5 , SO=5 . х у z
Слайд 17
Метод координат Расстояние от точки до плоскости Вычисляется по формуле: Расстояние от точки до плоскости. Расстояние между плоскостью и параллельной ей прямой. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Слайд 18
http://www.myshared.ru/slide/478172/ http://nsportal.ru/shkola/geometriya/library/2012/11/26/master-klass-nakhozhdenie-rasstoyaniya-mezhdu Интернет ресурсы:
({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V. Сочетательный закон ((lambda) – число): [lambda(vec{a}, vec{b})=(lambda
vec{a}, vec{b})]
(bullet) Скалярное произведение двух векторов (vec{a}
={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) можно вычислить с помощью координат этих векторов: [{large{(vec{a},
vec{b})=x_1x_2+y_1y_2+z_1z_2}}]
(bullet) Косинус угла между векторами (vec{a} ={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) вычисляется по формуле: [{large{cosangle(vec{a}, vec{b})=dfrac{x_1x_2+y_1y_2+z_1z_2}
{sqrt{x^2_1+y^2_1+z^2_1}cdot
sqrt{x^2_2+y^2_2+z^2_2}}}}]
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4. Про углы между прямыми, плоскостями}}})
(bullet) Если векторы (vec{a} ={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}) являются направляющими прямых (p) и (q), то косинус угла между этими прямыми равен: [cos phi=dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{sqrt{x^2_1+y^2_1+z^2_1}cdot sqrt{x^2_2+y^2_2+z^2_2}}]
(bullet) Если (vec{a}) — направляющий вектор прямой (p), а (vec{n}) — нормаль к плоскости (phi) (перпендикуляр к плоскости), то синус угла между прямой (p) и плоскостью (phi) равен модулю косинуса угла между векторами (vec{a}) и (vec{n}): [sin
angle(p, phi)=|cos angle(vec{a}, vec{n})|]
(bullet) Если две плоскости заданы уравнениями (a_1x+b_1y+c_1z+d_1=0) и (a_2x+b_2y+c_2z+d_2=0), то косинус угла между плоскостями ищется по формуле: [{large{cos phi=left| dfrac{a_1a_2+b_1b_2+c_1c_2}
{sqrt{a^2_1+b^2_1+c^2_1}cdot
sqrt{a^2_2+b^2_2+c^2_2}}right|}}]
({color{red}{textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}})
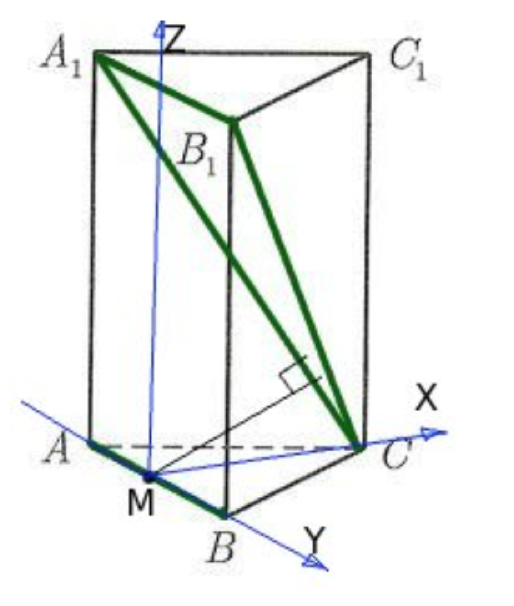
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi), (ax+by+cz+d=0) — уравнение плоскости (phi), то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac{|ax_0+by_0+cz_0+d|}{sqrt{a^2+b^2+c^2}}]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.


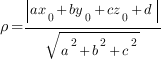
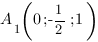
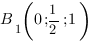
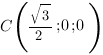
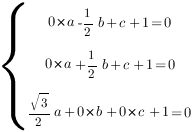
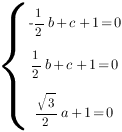
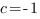
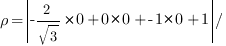
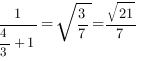
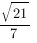


![Rendered by QuickLaTeX.com [ begin{cases}acdot 1+bcdot frac{1}{2}+ccdot 1 + d = 0, \ acdot 0+bcdot frac{1}{2}+ccdot 0 + d = 0, \ 0cdot 1+bcdot 0+ccdot 1 + d = 0.end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e089db7d19582bb1ee128bfcabd0b022_l3.png)
![Rendered by QuickLaTeX.com [ l = frac{|1cdot 0-2cdot 0-1cdot 0 + 1|}{sqrt{1^2+(-2)^2+(-1)^2}}=frac{1}{sqrt{6}}=frac{sqrt{6}}{6}. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-b0ce77d1513d51363c4922fcc802d45f_l3.png)