Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.
а) Докажите, что SA — высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Источник: Материалы для экспертов ЕГЭ 2016
2
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
3
В правильной четырёхугольной пирамиде SABCD все рёбра равны 5. На рёбрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA = AQ = RC = 2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Источник: Задания 14 (С2) ЕГЭ 2015
4
В правильной треугольной призме АВСА′B′C′ сторона основания АВ равна 6, а боковое ребро АА′ равно 3. На ребре АВ отмечена точка К так, что АК = 1. Точки М и L — середины рёбер А′С′ и В′С′ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости γ.
б) Найдите расстояние от точки С до плоскости γ.
Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ — 2016 по математике. Основная волна 06.06.2016. Вариант 410. Запад
5
В правильной четырёхугольной призме АВСDА1В1С1D1 сторона АВ основания равна 6, а боковое ребро АА1 равно На ребрах BC и C1D1 отмечены точки К и L соответственно, причём ВК = 4, C1L = 5. Плоскость γ параллельна прямой BD и содержит точки К и L.
а) Докажите, что прямая AC1 перпендикулярна плоскости γ.
б) Найдите расстояние от точки B1 до плоскости γ.
Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Юг (C часть).
Пройти тестирование по этим заданиям
Решение
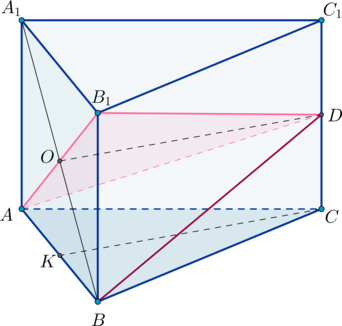
а) Плоскости MNK и DBC параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Докажем это. Рассмотрим прямые MN и KM плоскости MNK и прямые BC и DB плоскости DBC.
В треугольнике AOD: angle AOD = 90^circ и по теореме Пифагора AD=sqrt{DO^2 +AO^2}.
Найдём AO, используя то, что bigtriangleup ABC правильный.
AO=frac{2}{3}AO_1, где AO_1 — высота bigtriangleup ABC, AO_1 = frac{asqrt{3}}{2}, где a — сторона bigtriangleup ABC.
AO_1 = frac{6sqrt{3} cdot sqrt{3}}{2}=9, тогда AO=6, AD=sqrt{8^2 + 6^2}=10.
1. Так как frac{AK}{AD}=frac{5}{2} : 10=frac{1}{4}, frac{AM}{AB}=frac{3sqrt{3}}{2} : 6sqrt{3}=frac{1}{4} и angle DAB — общий, то bigtriangleup AKM sim ADB.
Из подобия следует, что angle AKM = angle ADB. Это соответственные углы при прямых KM и BD и секущей AD. Значит KM parallel BD.
2. Так как frac{AN}{AC}=frac{3 sqrt{3}}{2 cdot 6 sqrt{3}}=frac{1}{4}, frac{AM}{AB}=frac{1}{4} и angle CAB — общий, то bigtriangleup ANM sim bigtriangleup ACB.
Из подобия следует, что angle ANM = angle ACB. Эти углы соответственные при прямых MN и BC и секущей AC. Значит, MN parallel BC.
Вывод: так как две пересекающиеся прямые KM и MN плоскости MNK соответственно параллельны двум пересекающимся прямым BD и BC плоскости DBC, то эти плоскости параллельны — MNK parallel DBC.
б) Найдём расстояние от точки K до плоскости BDC.
Поскольку плоскость MNK параллельна плоскости DBC, то расстояние от точки K до плоскости DBC равно расстоянию от точки O_2 до плоскости DBC и оно равно длине отрезка O_2 H. Докажем это.
BC perp AO_1 и BC perp DO_1 (как высоты треугольников ABC и DBC), значит, BC перпендикулярна плоскости ADO_1, и тогда BC перпендикулярна любой прямой этой плоскости, например, O_2 H. По построению O_2Hperp DO_1, значит, O_2H перпендикулярна двум пересекающимся прямым плоскости BCD, и тогда отрезок O_2 H перпендикулярен плоскости BCD и равен расстоянию от O_2 до плоскости BCD.
В треугольнике O_2HO_1:O_2H=O_{2}O_{1}sinangle HO_{1}O_{2}.
O_{2}O_{1}=AO_{1}-AO_{2}., frac{AO_2}{AO_1}=frac{1}{4}, AO_{2}=frac{AO_1}{4}=frac{9}{4}.
O_{2}O_{1}=9-frac{9}{4}=frac{27}{4}.
sin angle DO_{1}A= frac{DO}{DO_{1}}= frac{8}{sqrt{64+3^2}}= frac{8}{sqrt{73}}.
O_2H=frac{27}{4} cdot frac{8}{sqrt{73}}=frac{54}{sqrt{73}}.
Ответ
frac{54}{sqrt{73}}
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение расстояний от точки до прямой/плоскости
(blacktriangleright) Расстояние от точки до прямой/плоскости — длина перпендикуляра, опущенного из этой точки на прямую/плоскость.
(blacktriangleright) Т.к. все точки одной из параллельных прямых находятся на одинаковом расстоянии от другой прямой, то расстояние между параллельными прямыми — это длина перпендикуляра, опущенного из любой точки одной прямой ко второй прямой.
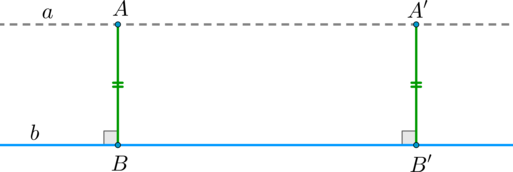
Таким образом, иногда бывает удобно искать расстояние между точкой (A) и прямой (b) как расстояние между прямой (a (aparallel b,
asubset A)) и прямой (b) (то есть опускать перпендикуляр не из точки (A), а из какой-нибудь другой “более удобной” точки на прямой (a)).
(blacktriangleright) Т.к. все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости, то расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости к другой плоскости.
(blacktriangleright) Т.к. все точки прямой, параллельной плоскости, находятся на одинаковом расстоянии от этой плоскости, то расстояние между параллельными прямой и плоскостью — это длина перпендикуляра, опущенного из любой точки прямой к плоскости.
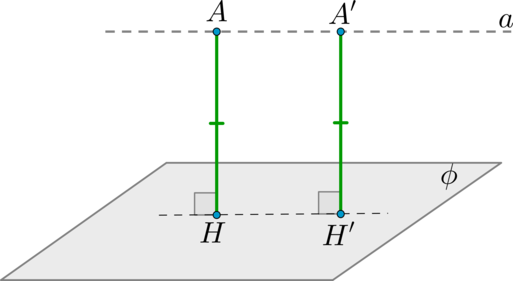
Таким образом, иногда бывает удобно искать расстояние между точкой (A) и плоскостью (phi) как расстояние между прямой (a (aparallel
phi, asubset A)) и плоскостью (phi) (то есть опускать перпендикуляр не из точки (A), а из какой-нибудь другой “более удобной” точки на прямой (a)).
Задание
1
#6927
Уровень задания: Легче ЕГЭ
Дана треугольная пирамида (SABC), причем грани (SAB) и (SAC) представляют собой равные равнобедренные треугольники с прямыми углами при вершине (A). Найдите расстояние от точки (A) до грани (SBC), если высота пирамиды равна (h) и равна (BC).
Из условия задачи следует, что:
1) (SAperp AB, AC Rightarrow SAperp (ABC));
2) (SA=AB=AC=h=BC);
3) (SB=SC=hsqrt2).
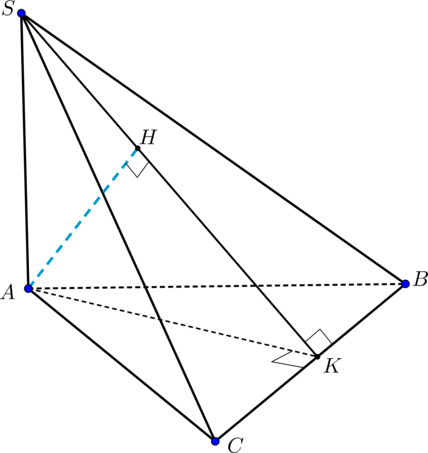
Т.к. (triangle BAC) равнобедренный, то (AKperp BC, K) – середина (BC). Аналогично, (SKperp BC). Таким образом, перпендикуляр (AH) на плоскость (SBC) упадет на прямую (SK) (удовлетворяет теореме о трех перпендикулярах: (HK) – проекция, (AK) – наклонная, обе перпендикулярны (BC)).
По теореме Пифагора (AK=dfrac{hsqrt3}{2}).
Следовательно, (mathrm{tg}, angle
SKA=dfrac{SA}{AK}=dfrac{2sqrt3}{3}=dfrac{AH}{HK}).
Значит, (AH=2sqrt3x, HK=3x).
По теореме Пифагора из (triangle AHK) находим (x=dfrac{1}{2sqrt7}h Rightarrow AH=sqrt{dfrac{3}{7}}h)
Ответ:
(sqrt{dfrac{3}{7}}h)
Задание
2
#3143
Уровень задания: Сложнее ЕГЭ
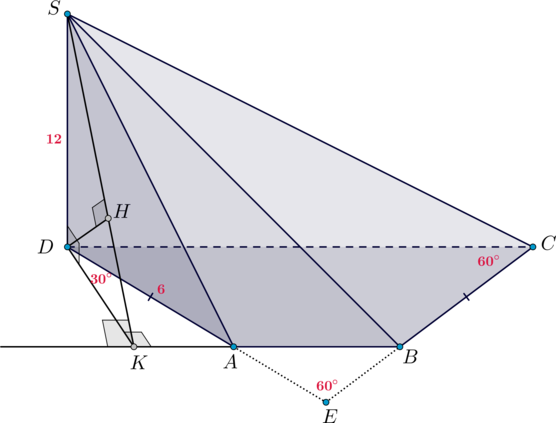
В основании четырехугольной пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), причем (AD=BC=6), (CD>AB). Угол между прямыми (AD) и (BC) равен (60^circ). Известно, что (SD=12) – высота пирамиды.
Найдите расстояние от точки (C) до грани (SAB).
Так как (CDparallel AB) – основания трапеции, то (CD) параллельна плоскости (SAB), в которой находится прямая (AB). Следовательно, расстояние от любой точки прямой (CD) до плоскости (SAB) будет одинаковым. Найдем расстояние до плоскости (SAB) от точки (D).
Так как (SD) – высота пирамиды, то (SDperp (ABC)). Проведем (DKperp AB) (точка (K) упадет на продолжение отрезка (AB) за точку (A)).
Если (E) – точка пересечения прямых (AD) и (BC), то (angle
AEB=60^circ). Так как также (angle BAE=angle ABE) (так как трапеция равнобедренная), то (triangle AEB) равносторонний и (angle BAE=60^circ). Следовательно, и (angle ADC=angle
BCD=60^circ).
По теореме о трех перпендикулярах (SKperp AB) (заметим, что (SKin
(SAB))). Тогда перпендикуляр (DH) из точки (D) на плоскость (SAB) упадет на (SK) (в противном случае по теореме о трех перпендикулярах проекция (HK) наклонной (DK) будет перпендикулярна (AB) и тогда будут существовать в одной плоскости два перпендикуляра (SK) и (HK) к прямой (AB), что невозможно).
Таким образом, необходимо найти (DH).
Из прямоугольного треугольника (DAK) [cos angle ADK=cos 30^circ=dfrac{DK}{DA} quadRightarrowquad
DK=3sqrt3.] Тогда по теореме Пифагора из (triangle SDK): [SK=sqrt{SD^2+DK^2}=sqrt{144+27}=3sqrt{19}] Тогда из этого же треугольника [DKcdot SD=DHcdot SK quadRightarrowquad DH=dfrac{12sqrt3}{sqrt{19}}.]
Ответ:
(dfrac{12sqrt3}{sqrt{19}})
Задание
3
#1248
Уровень задания: Сложнее ЕГЭ
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S). Через точку пересечения диагоналей основания провели плоскость (alpha) перпендикулярно ребру (SA). Найдите расстояние от точки (N) до плоскости (alpha), если (N) – середина (AD=2sqrt2), а высота пирамиды равна (11).
1) Построим сечение пирамиды плоскостью (alpha). Т.к. (alphaperp
SA), то (SA) перпендикулярна двум пересекающимся прямым, лежащим в (alpha). Обозначим (ACcap BD=O). Проведем (OKperp SA).
По теореме о трех перпендикулярах (SAperp BD) как наклонная ((SOperp (ABC), OAperp BD) – проекция).
Таким образом, имеем две пересекающиеся прямые (OK) и (BD) из плоскости (alpha). Значит, сечением является треугольник (BKD).
2)Проведем (MNparallel BD), следовательно, (MNparallel alpha). Т.к. расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то (rho(N, alpha)=rho(Q, alpha)) ((rho) — расстояние).
Т.к. по условию (SAperp alpha), то проведем (QHparallel SA
Rightarrow QHperp alpha).
По построению (MN) – средняя линия (triangle BAD), следовательно, (AQ=QO Rightarrow QH) – средняя линия (triangle KAO Rightarrow
QH=dfrac{1}{2}AK).
Рассмотрим (triangle SAO):
(AO=2).
Из (triangle AKO sim triangle ASO Rightarrow
dfrac{AK}{AO}=dfrac{AO}{AS} Rightarrow AK=dfrac{4sqrt5}{25}
Rightarrow QH=dfrac{2sqrt5}{25}).
Ответ:
(dfrac{2sqrt5}{25})
Задание
4
#3195
Уровень задания: Сложнее ЕГЭ
В правильной треугольной призме (ABCA_1B_1C_1) стороны основания равны (6), боковые ребра равны (8), точка (D) – середина (CC_1). Найдите расстояние от вершины (B) до плоскости (AB_1D).
(Задача от подписчиков)
Найдем расстояние от точки (B) до плоскости (AB_1D) через объем пирамиды (BAB_1D).
Так как призма правильная, то боковые грани – равные прямоугольники. Следовательно, так как (CD=DC_1), то (triangle
ACD=triangle B_1C_1D), откуда (AD=DB_1). Следовательно, если (O) – точка пересечения диагоналей (AB_1) и (A_1B), то (DOperp AB_1) (медиана и высота в равнобедренном треугольнике).
Пусть (K) – середина (AB). Тогда (CKparallel DO). Значит, так как (CKperp AB), то (DOperp AB). Отсюда (DO) перпендикулярна двум пересекающимся прямым (AB_1) и (AB) в плоскости (ABB_1), следовательно, (DOperp(ABB_1)). Значит, (DO) – высота пирамиды (BAB_1D) к основанию (ABB_1).
Следовательно, [dfrac 13cdot DOcdot S_{ABB_1}=V_{BAB_1D}=dfrac 13cdot hcdot
S_{AB_1D},] где (h) – расстояние от точки (B) до ((AB_1D)).
1) (S_{ABB_1}=0,5cdot ABcdot BB_1=0,5cdot 6cdot 
2) (DO=CK) как противоположные стороны параллелограмма (DOKC) ((DOparallel CK), (DCparallel OK)).
3) (CK=0,5sqrt3AB=3sqrt3).
4) (AB_1=sqrt{AB^2+BB_1^2}=10).
5) (S_{AB_1D}=0,5cdot DOcdot AB_1=0,5cdot 3sqrt3cdot 10).
Следовательно: [h=dfrac{3sqrt3cdot 0,5cdot 6cdot 8}{0,5cdot 3sqrt3cdot 10}=4,8]
Ответ: 4,8
Задание
5
#1250
Уровень задания: Сложнее ЕГЭ
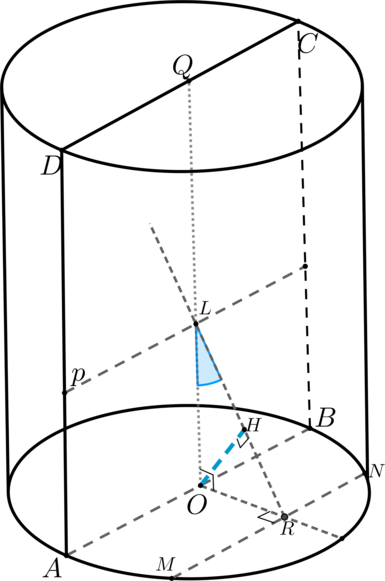
В цилиндре параллельно диаметру (AB=10) в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках (M) и (N), причем (MN=6). Через отрезок (MN) проведена плоскость (alpha) под углом (15^o) к плоскости осевого сечения (ABCD). Найдите расстояние от центра нижнего основания до плоскости (alpha).
1) Т.к. (MNparallel AB), то плоскость (alpha) пересечет плоскость (ABCD) по прямой (p), параллельной (AB) (если это не так, то (pcap
AB = K Rightarrow Kin text{нижнему основанию и } Kin alpha
Rightarrow K in MN Rightarrow ABcap MN ne varnothing), что противоречит условию).
Обозначим за (OQ) – ось цилиндра. Тогда (OQperp AB Rightarrow
OQperp p) ((OQcap p =L)). Проведем (ORperp MN Rightarrow ) по теореме о трех перпендикулярах (RLperp MN Rightarrow RLperp p
Rightarrow angle RLO) – угол между плоскостями (ABCD) и (alpha).
2) Т.к. (ORperp MN text{ и } LRperp MN), то перпендикуляр из точки (O) на плоскость (alpha) упадет на прямую (LR).
Рассмотрим (triangle OMR: OM=5, MR=3, angle ORM=90^circ
Rightarrow OR=4).
Рассмотрим (triangle LOR: angle HOR=angle RLO=15^circ
Rightarrow OH=ORcdot cos15^circ=4cdot
cos{(45^circ-30^circ)}=sqrt6+sqrt2).
Ответ:
(sqrt6+sqrt2).
Задание
6
#1249
Уровень задания: Сложнее ЕГЭ
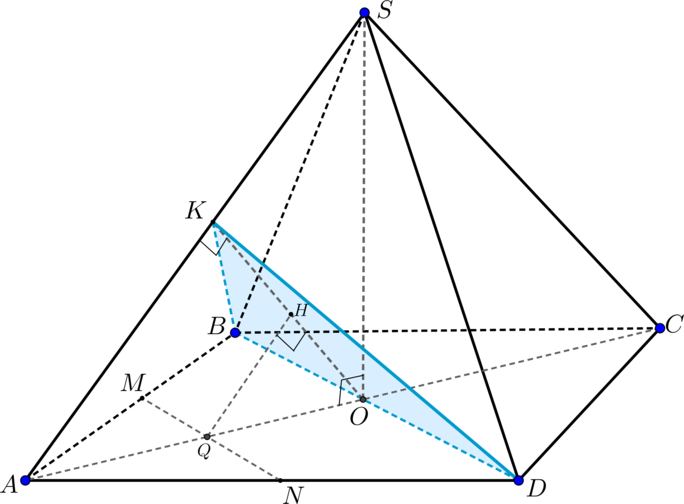
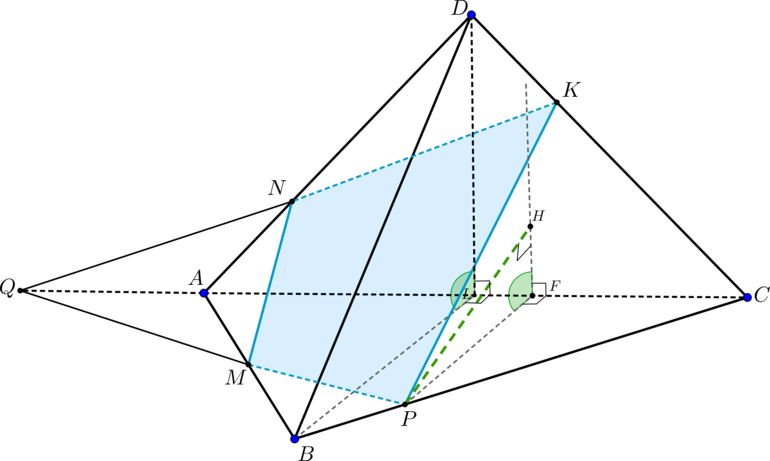
(ABCD) – правильный тетраэдр с ребром (6). (M, N, K) – такие точки на ребрах (AB, AD, CD) соответственно, что (AM=MB, DN=2NA=CK). Плоскость (MNK) пересекает ребро (BC) в точке (P). Найдите расстояние от точки (P) до плоскости (ACD).
1) По условию (ABCD) представляет собой правильную треугольную пирамиду, все ребра которой равны (6). Найдем, в каком отношении точка(P) делит отрезок (BC). Для этого построим сечение пирамиды плоскостью (MNK). Продлим прямую (NK) до пересечения с прямой (AC) – получим точку (Q). Соединив точки (Q) и (M), получим линию пересечения основания – отрезок (MP) (сечением является четырехугольник (MNKP)).
По теореме Менелая для (triangle ADC) и прямой (QK) имеем:
(dfrac{AN}{ND}cdot dfrac{DK}{KC}cdot dfrac{CQ}{QA}=1
Rightarrow QA=2).
Аналогично для (triangle ABC) и прямой (QP):
(dfrac{BM}{MA}cdot dfrac{AQ}{QC}cdot dfrac{CP}{PB}=1
Rightarrow BP=dfrac{6}{5}).
2) Проведем (PHperp ADC) и (PFperp AC). Тогда по теореме о трех перпендикулярах (HFperp AC), следовательно, (angle HFP=angle
(ABC, ACD)=angle alpha). Найдем (PH) из треугольника (PHF). Для этого найдем (PF) и (angle alpha).
Проведем (BLperp AC), тогда (angle BLD=angle alpha). Треугольник (BLD) – равнобедренный ((BL=LD=3sqrt3, BD=6)). По теореме косинусов найдем (cos angle alpha=dfrac{1}{3})
Тогда (sin angle alpha = dfrac{2sqrt2}{3}=dfrac{PH}{PF}).
(triangle BLC sim triangle PFC Rightarrow
PF=dfrac{12sqrt3}{5})
Таким образом, (PH=dfrac{8sqrt{6}}{5}).
Ответ:
(dfrac{8sqrt{6}}{5}).
Задания, предлагающие школьнику найти расстояние от точки до прямой, в ЕГЭ встречаются ежегодно. При этом умение выполнять подобные задачи требуется выпускникам, сдающим как базовый уровень экзамена по математике, так и профильный. Научившись находить расстояние от точки до плоскости, в ЕГЭ школьник сможет правильно выполнить задание и получить заветные баллы.
«Прокачать» навыки и улучшить знания в таком непростом разделе геометрии, как стереометрия, вам поможет наш образовательный проект. «Школково» предлагает учащимся и их преподавателям по-новому выстроить процесс подготовки к сдаче единого госэкзамена.
Для того чтобы вы могли во время ЕГЭ правильно и с минимальными временными затратами решать задачи, где требуется найти расстояние от точки до прямой, мы предлагаем прежде всего повторить определения и основные правила. Для этого достаточно посетить раздел «Теоретическая справка». Здесь мы разместили материал, составленный нашими специалистами специально для учащихся с различным уровнем подготовки.
Затем для закрепления полученных знаний и отработки навыков выполните задания на нахождение расстояния от точки до плоскости в ЕГЭ; вы можете это сделать вне зависимости от того, где вы находитесь: в Москве или другом городе. Богатая подборка задач представлена в разделе «Каталог».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ЕГЭ Профиль №13. Расстояние от точки до прямой. Расстояние от точки до плоскости
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Расстояние от точки до прямой. Расстояние от точки до плоскости
Расстояние от точки до прямой. Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую. Расстояние от точки до прямой можно вычислить, как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот. При этом если длины сторон треугольника все разные a, b, c (треугольник не равносторонний и не равнобедренный), то высоту треугольника, например, к стороне a можно искать по следующему алгоритму: 1) по теореме косинусов находим косинус угла между сторонами a и b; 2) зная косинус этого угла, используя основное тригонометрическое тождество, найти его синус; 3) синус найденного угла есть отношение искомой высоты к стороне b. В прямоугольном треугольнике высота к гипотенузе равна произведению катетов, деленному на гипотенузу.
Расстояние от точки до плоскости. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость. Расстояние от точки M до плоскости α: 1) равно расстоянию до плоскости α от произвольной точки P, лежащей на прямой l, которая проходит через точку M и параллельна плоскости α; 2) равно расстоянию до плоскости α от произвольной точки P, лежащей на плоскости α, которая проходит через точку M и параллельна плоскости α. Метод объемов: Если объем пирамиды ABCS равен ({V_{ABCS}}), то расстояние от точки S до плоскости ABC можно найти используя формулу объема пирамиды: ({V_{ABCS}} = frac{1}{3}{S_{ABC}} cdot H), где H – расстояние от точки S до плоскости ABC.
Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра. Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра, которое равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
1В. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной (AB = 4) и диагональю (BD = 7). Все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребре AS – точка F так, что (SF = BE = 3.)
а) Докажите, что плоскость CEF параллельна ребру SB.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
ОТВЕТ: (frac{{2sqrt {15} }}{7}).
2В. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а высота призмы равна 2. На ребрах B1C1 и AB отмечены точки P и Q соответственно, причем (P{C_1} = 3,quad AQ = 4.) Плоскость A1PQ пересекает ребро BC в точке М.
а) Докажите, что точка М является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A1PQ.
ОТВЕТ: (frac{{3sqrt {30} }}{5}).
3В. На ребрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причем (DP = 4,;;{B_1}Q = 3.) Плоскость APQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СC1.
б) Найдите расстояние от точки С до плоскости APQ.
ОТВЕТ: (frac{{12sqrt {26} }}{{13}}).
4В. В основании прямой треугольной призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с прямым углом С, (AC = 4,;;BC = 16,) (A{A_1} = 4sqrt 2 .) Точка Q – середина ребра A1B1, а точка P делит ребро B1C1 в отношении 1 : 2, считая от вершины С1. Плоскость APQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СC1.
б) Найдите расстояние от точки А1 до плоскости APQ.
ОТВЕТ: (frac{{32sqrt {57} }}{{57}}).
5В. В правильной четырехугольной призме ABCDA1B1C1D1 сторона АВ основания равна 8, а боковое ребро AA1 равно (4sqrt 2 ). На ребрах BC и С1D1 отмечены точки K и L соответственно, причем (BK = {C_1}L = 2.) Плоскость (alpha ) параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A1C перпендикулярна плоскости (alpha ).
б) Найдите расстояние от точки B до плоскости (alpha ).
ОТВЕТ: (frac{{2sqrt {10} }}{5}).
6В. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а боковое ребро АА1 равно (3sqrt 6 ). На ребрах АВ и В1С1 отмечены точки К и L соответственно, причем (AK = 2,;;{B_1}L = 4.) Точка М – середина ребра А1С1. Плоскость (alpha ) параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости (alpha ).
б) Найдите расстояние от точки С до плоскости (alpha ).
7В. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что (PA = AQ = RC = 2).
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от точки D до плоскости PQR.
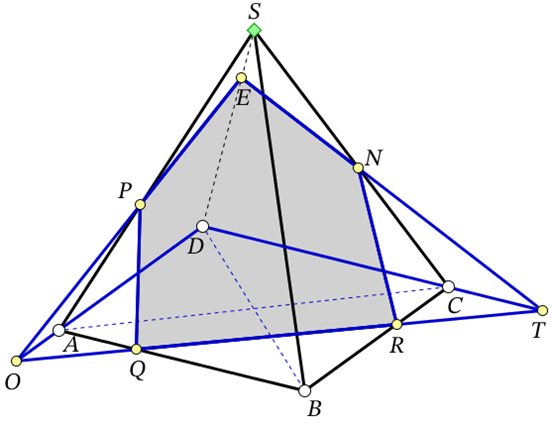
(frac{{BQ}}{{QA}} = frac{{BR}}{{RC}},,,, Rightarrow ,,,,QRparallel AC,) но (AC bot BD,) тогда (DB bot QR.) Следовательно, (SD bot QR) по теореме о трёх перпендикулярах.
(left. {begin{array}{*{20}{c}}{SD bot QR}\{SD bot PQ}end{array}} right},,, Rightarrow ,,,,SD bot PQR.)
б) Искомое расстояние DE. Треугольник SEP прямоугольный с гипотенузой SP и (angle PSE = {60^ circ }.) Тогда (cos {60^ circ } = frac{{SE}}{{SP}},,,, Leftrightarrow ,,,,SE = frac{3}{2}) и (DE = DS — SE = 5 — frac{3}{2} = frac{7}{2}.)
Ответ: (frac{7}{2}.)
8В. В правильной треугольной пирамиде SABC сторона основания AB равна 30, а боковое ребро SA равно 28. Точки M и N – середины ребер SA и SB соответственно. Плоскость (alpha ) содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость (alpha ) делит медиану CE основания в отношении 5 : 1, считая от точки С.
б) Найдите расстояние от точки А до плоскости (alpha ).
ОТВЕТ: (frac{{5sqrt 3 }}{2}).
9В. В правильной четырёхугольной призме ABCDA1B1C1D1 основание ABCD — квадрат. Точка M — центр боковой грани BCC1B1.
а) Докажите, что плоскость A1D1M делит диагональ AC1 в отношении 2 : 1, считая от точки A.
б) Найдите расстояние от точки M до прямой BD1, если сторона основания призмы равна 6, а боковое ребро равно 3.
10В. Дана треугольная призма ABCA1B1C1 с основаниями ABC и A1B1C1. Точка M — центр боковой грани BCC1B1.
а) Постройте точку пересечения прямой A1M с плоскостью ABC.
б) Найдите расстояние от точки M до прямой AB1, если призма прямая, ABC — прямоугольный треугольник с прямым углом C, а диагонали боковых граней AA1B1B и BB1C1C равны 17 и 15 соответственно.
11В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1.
а) Докажите, что плоскость CA1F1 делит ребро BB1 пополам.
б) Найдите расстояние от точки C до прямой A1F1, если стороны основания призмы равны 5, а боковые рёбра равны 11.
12В. Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость α, проходящая через ребро AB и середину ребра SE, делит ребро SC в отношении 2 : 1, считая от вершины S.
б) Найдите расстояние от точки S до плоскости α, если сторона основания пирамиды равна (2sqrt 3 ), а угол между боковой гранью и плоскостью основания пирамиды равен 60º.
13В. Основание пирамиды DABC — прямоугольный треугольник ABC с прямым углом C. Высота пирамиды проходит через середину ребра AC, а боковая грань ACD — равносторонний треугольник.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра AD, — прямоугольный треугольник.
б) Найдите расстояние от вершины D до этой плоскости, если M — середина ребра AD, а высота пирамиды равна 6.
14В. Основание пирамиды SABCD — прямоугольник ABCD. Высота SH пирамиды лежит в плоскости CSD.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра SA, отличную от S и A, — прямоугольная трапеция.
б) Найдите расстояние от вершины S до этой плоскости, если H — середина ребра CD, M — середина ребра SA, (SC = CD,;;SH = 2sqrt 3 ).
15В. Основание пирамиды SABCD — квадрат ABCD. Боковое ребро SD перпендикулярно плоскости основания. Точка M — середина высоты пирамиды.
а) Докажите, что прямая SB параллельна плоскости ACM.
б) Найдите расстояние от точки B до плоскости ACM, если (AB = 
16В. Основание пирамиды SABCD — прямоугольник ABCD. Боковое ребро SD перпендикулярно плоскости основания.
а) Докажите, что прямые SC и AD перпендикулярны.
б) Пусть M — середина высоты пирамиды. Найдите расстояние от точки B до плоскости ACM, если AB = 8, BC = 6, а синус угла между плоскостью ACM и плоскостью основания пирамиды равен 5/6.
17В. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Высота пирамиды втрое больше стороны основания и проходит через точку E.
а) Докажите, что угол между боковой гранью ASB и плоскостью основания равен 60º.
б) Найдите расстояние от точки C до плоскости ASB, если сторона основания пирамиды равна 4.
18В. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF c центром O. Отрезок OA1 — высота призмы.
а) Докажите, что плоскость FF1E перпендикулярна плоскости основания призмы.
б) Найдите расстояние от точки A до плоскости BCC1, если сторона основания призмы равна (2sqrt 3 ).
19В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1.
а) Докажите, что плоскость ADC1 перпендикулярна плоскости FBB1.
б) Найдите расстояние от точки C до плоскости ADC1, если AA1 = 4, а косинус угла между прямой AC1 и плоскостью ABC равен (frac{3}{{sqrt {13} }}).
20В. Дана правильная четырёхугольная призма ABCDA1B1C1D1 со стороной основания (sqrt 2 ) и боковым ребром 2. Точки M и N — середины рёбер A1B1 и CC1 соответственно.
а) Докажите, что MN ⊥ BC1.
б) Найдите расстояние от точки M до плоскости BC1D.
ОТВЕТ: (frac{{3sqrt 5 }}{5}).
21В. Основание пирамиды SABCD — равнобедренная трапеция ABCD с основаниями AD и BC, причём AD = 2BC = 2AB. Высота SH пирамиды проходит через точку пересечения прямых AB и CD.
а) Докажите, что треугольник SBD прямоугольный.
б) Найдите расстояние от точки C до плоскости ASD, если SH = BC = 4.
22В. Основание пирамиды SABCD — прямоугольная трапеция ABCD с большим основанием AD и прямым углом D. Высота SH пирамиды проходит через точку пересечения прямых AB и CD.
а) Докажите, что грань ASD — прямоугольный треугольник.
б) Найдите расстояние от точки B до плоскости ASD, если AD = 3BC = 3, ∠BAD = 45º и SH = 4.
23В. Боковые рёбра пирамиды SABC с вершиной S попарно перпендикулярны.
а) Докажите, что высота SH пирамиды проходит через точку пересечения высот основания ABC.
б) Найдите SH, если боковые рёбра равны 2, 2 и (7sqrt 2 ).
24В. Боковые рёбра пирамиды SABC с вершиной S попарно перпендикулярны, M — произвольная точка на ребре BC.
а) Докажите, что плоскости AMS и BSC перпендикулярны.
б) Высота SH пирамиды равна 12. Прямая AH пересекает ребро BC в точке K. Найдите расстояние от точки K до прямой AS, если AS = 20.
25В. Плоскость проходит через середины боковых рёбер DA и DC треугольной пирамиды DABC и точку пересечения медиан основания ABC.
а) Постройте точку пересечения этой плоскости с прямой DB.
б) Найдите расстояние от точки A до этой плоскости, если все рёбра пирамиды равны (3sqrt 6 ).
26В. Плоскость проходит через середины сторон AD и BC основания ABCD правильной четырёхугольной пирамиды SABCD и точку пересечения медиан боковой грани CSD.
а) Постройте точку пересечения прямой AS с этой плоскостью.
б) Найдите расстояние от точки B до этой плоскости, если все рёбра пирамиды равны (2sqrt 3 ).
27В. Все грани параллелепипеда ABCDA1B1C1D1 — равные ромбы, причём плоские углы при вершине C острые.
а) Докажите, что AA1 ⊥ BD.
б) Найдите расстояние от вершины C до плоскости A1B1C1, если плоские углы при вершине C равны 60°, а (A{A_1} = sqrt 6 ).
28В. Основание наклонной призмы ABCA1B1C1 — равносторонний треугольник ABC. Боковые грани AA1B1B и AA1C1C — равные ромбы с острым углом при общей вершине A.
а) Докажите, что боковая грань BB1C1C — квадрат.
б) Найдите расстояние от вершины A до плоскости BB1C1, если ∠CAA1 = 60°, а сторона основания призмы равна (sqrt 2 ).
29В. Основание пирамиды SABCD — параллелограмм ABCD. Боковые рёбра SA и SD равны. Точка M лежит на боковом ребре SC и не совпадает с его концами. Плоскость α проходит через точку M параллельно прямым BC и SA.
а) Докажите, что сечение пирамиды плоскостью α — равнобедренная трапеция.
б) Найдите расстояние от точки A до плоскости α, если боковая сторона этой трапеции равна меньшему основанию, а все рёбра пирамиды равны 1.
ОТВЕТ: (frac{{sqrt 6 }}{6}).
30В. Точка K лежит на стороне AB основания ABCD правильной четырёхугольной пирамиды SABCD, все рёбра которой равны. Плоскость α проходит через точку K параллельно плоскости ASD. Сечение пирамиды плоскостью α — четырёхугольник, в который можно вписать окружность.
а) Докажите, что BK = 2AK.
б) Найдите расстояние от вершины S до плоскости α, если все рёбра пирамиды равны 1.
ОТВЕТ: (frac{{sqrt 6 }}{9}).
31В. В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM = DN = 4 и AK = 3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки K до плоскости SBC.
ОТВЕТ: (frac{{12sqrt 5 }}{5}).
32В. ABCA1B1C1 — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.
а) Докажите что периметр сечения призмы плоскостью α больше 40.
б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.
ОТВЕТ: (frac{{24sqrt {273}}}{91}).
33В. Точка O — центр основания ABCDEF правильной шестиугольной пирамиды SABCDEF. Точки K, L, M, T — середины отрезков AF, SF, SD, MK соответственно.
а) Докажите, что точка T лежит на отрезке LO.
б) Найдите CT, если сторона основания пирамиды равна 4, а высота пирамиды равна 48.
Описание презентации по отдельным слайдам:
-
1 слайд
Методы решения
геометрических задач
Подготовил: учитель математики МОУ «СОШ №10 с. Солдато-Александровского» Кобзев Д.А.
2012 – 2013 уч.г.
ЕГЭ, задание С2
(Расстояние от точки до плоскости) -
2 слайд
Расстояние от точки до плоскости
Методы
Поэтапно-вычислительный
метод
Метод параллельных
прямых и плоскостей
Векторный метод
Координатный метод
Метод объемов -
3 слайд
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости А1В1С.
B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
G
H
Высота АН в треугольнике АА1G – искомое расстояние.
Из прямоуг. треугольника ADE:
Из прямоуг. треугольника AGA1:
Ответ: -
4 слайд
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки C1 до плоскости AB1C
B
D
C
A
A1
B1
C1
D1
то
Поэтому искомое расстояние h равно расстоянию от произвольной точки А1С1 до плоскости АВ1С.
Е
О
О1
h
Обозначим расстояние от О1 до (АВ1С) через h.
Покажем, что О1Е ┴ АВ1С.
О1Е – перпендикуляр к (АВ1С), а О1Е = h
Так как
то из прямоугольного треугольника ОВ1О1:
Искомое расстояние:
Ответ: -
5 слайд
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1
D
C
B
A
A1
B1
D1
M
C1
Пусть
тогда
Выразим векторы
через
Пусть -
6 слайд
D
C
B
A
A1
B1
D1
M
C1
Имеем:
Отсюда получаем:
Таким образом
Ответ: -
7 слайд
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости DEF1
B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
O
z
y
x
Введем систему координат и найдем координаты точек:
уравнение (DEF1).
Подставим координаты точек D, E, F1 в уравнение:
уравнение (DEF1):
Ответ: -
8 слайд
Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние от точки C до плоскости BDC1
D
C
B
A
A1
B1
C1
D1
Q
R
Расстояние х равно высоте CQ, опущенной в пирамиде BCDC1 из вершины С на основание BDC1
Треугольник BDC1 – равносторонний.
Так как V1 = V2, то получаем уравнение:
Ответ: