Всего: 95 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
В кубе ABCDA1B1C1D1 все ребра равны 1.
а) Докажите, что расстояние от точки C до плоскости меньше, чем расстояние от точки C до прямой
б) Найдите расстояние от точки C до прямой AD1
Длины ребер AB, AA1 и AD прямоугольного параллелепипеда ABCDA1B1C1D1 равны соответственно 12, 16 и 15.
а) Докажите, что расстояние от вершины до прямой
больше, чем расстояние от вершины A1 до прямой BD1
б) Найдите расстояние от вершины A1 до прямой BD1.
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.
Длины ребер BC, BB1 и BA прямоугольного параллелепипеда ABCDA1B1C1D1 равны соответственно 8, 12 и 9.
а) Докажите, что расстояние от вершины до прямой
больше, чем расстояние от вершины
до прямой
б) Найдите расстояние от вершины D1 до прямой A1C.
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 3, а боковые ребра равны 4.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки С до прямой D1E1.
В правильной шестиугольной призме стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точки В до прямой
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 4, найдите расстояние от точки A до прямой B1C1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите расстояние от точки B до плоскости DEA1.
В правильной треугольной призме ABCA1B1C1 высота равна 1, а ребро основания равно 2.
а) Докажите, что точки A и равноудалены от плоскости
б) Найдите расстояние от точки A1 до прямой BC1.
В правильной треугольной призме ABCA1B1C1 высота равна 2, сторона основания равна 1.
а) Докажите, что точки и B равноудалены от плоскости
б) Найдите расстояние от точки B1 до прямой AC1.
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно
а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 9. (Часть C).
В конусе с вершиной в точке Р высота РО = В его основании проведена
хорда АВ, отстоящая от точки О на расстоянии, равном 3. Известно, что радиус
основания конуса равен 5.
а) Докажите, что расстояние от точки Р до прямой АВ вдвое меньше длины отрезка АВ.
б) Найдите радиус сферы, описанной около пирамиды РОАВ.
Источник: А. Ларин: Тренировочный вариант № 237.
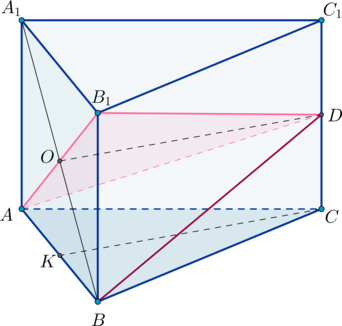
Дан куб ABCDA1B1C1D1. Точка K — середина ребра C1D1.
а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.
б) Найдите угол между плоскостями KBA1 и BCC1.
В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 1, высота SO = 2, точка M — середина ребра BS.
а) Докажите, что AM параллельна FN, где N — середина ребра SE.
б) Найдите расстояние от точки E до прямой AM.
Источник: А. Ларин. Тренировочный вариант № 282.
Дан куб ABCDA1B1C1D1. Точка K — середина ребра C1D1.
а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.
б) Найдите угол между плоскостями KBA1 и ADD1.
Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между этими хордами равно
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно
а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.
б) Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1 причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что
а) Докажите, что угол между прямыми BC и AC1 равен
б) Найдите расстояние от точки B до AC1.
Источник: ЕГЭ — 2018. Основная волна 25.06.2018. Вариант 557 (C часть)., Задания 14 (С2) ЕГЭ 2018
В кубе ABCDA1B1C1D1 с ребром, равным 6, на ребре AA1 взята точка M так, что На ребре D1C1 взята точка N так, что
а) Докажите, что прямые MB1 и CN перпендикулярны.
б) Найдите расстояние от точки M до прямой CN.
Источник: А. Ларин. Тренировочный вариант № 385.
В треугольной пирамиде длины двух непересекающихся рёбер равны 12 и 4, а остальные рёбра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.
Источник: А. Ларин: Тренировочный вариант № 65.
Всего: 95 1–20 | 21–40 | 41–60 | 61–80 …
Занятие № 2
Расстояния в пространстве:
расстояние от точки до плоскости в пространстве
Теория
Определение
Длина перпендикуляра, проведенного из точки А к плоскости α называется расстоянием от точки А до плоскости α.
α; А
α.
Определение
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Теорема (признак перпендикулярности прямой и плоскости)
Если прямая, перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Теорема (признак перпендикулярности плоскостей)
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Методы решения задач
При вычислении расстояния от точки до плоскости необходимо выполнить следующее:
- доказать, что некоторая прямая, проходящая через данную точку А, перпендикулярна плоскости α;
- вычислить длину перпендикуляра от точки А до плоскости α.
1. Метод построения перпендикуляра (поэтапных вычислений)
Для нахождения расстояния от точки А до плоскости α находят перпендикуляр АА‘, опущенный из точки А на плоскость α.
Если нахождение длины перпендикуляра не вытекает непосредственно из условия задачи, то на плоскости α выбирают какую-нибудь прямую а, проходящую через точку А‘, и находят длину перпендикуляра АА‘, опущенного из точки А на прямую а. Для этого используют теорему Пифагора или другие теоремы и формулы.
Задача № 1
В единичном кубе A…D1 найдите расстояние от точки А до плоскости BDA1.
Решение
Построим перпендикуляр из точки А к плоскости BDA1.
- Точка О — точка пересечения диагоналей основания куба,
следовательно, О – середина отрезка BD и АО BD.
Прямая BD перпендикулярна прямой АО, лежащей в плоскости АОА1, значит, прямая BD перпендикулярна плоскости АОА1 (по определению).
- Плоскость BDA1 проходит через прямую BD, прямая BD
перпендикулярна плоскости АОА1, следовательно, плоскости BDA1 и АОА1 перпендикулярны (по признаку перпендикулярности плоскостей).
- Искомый перпендикуляр, опущенный из точки А на плоскость BDA1
есть отрезок АН, проведенный из точки А на линию пересечения плоскостей BDA1 и АОА1 — прямую А1О (по определению).
- АН – высота прямоугольного треугольника АОА1 (А1А
АО), в
котором АА1 = 1 (по условию), АО = (половина диагонали основания), ОА1 =
(по теореме Пифагора).
Высоту АН можно вычислить различными способами.
Способ 1 (через площади треугольников).
Для площади S этого треугольника АОА1 имеют место равенства
и
AOAA1 = A1 O
AН,
Откуда находим АН = .
Способ 2 (через подобие треугольников).
Треугольники АОА1 и НОА подобны по двум углам (. Следовательно,
. Откуда находим АН =
.
Способ 3 (через синус угла).
Из прямоугольных треугольников АОА1 и НОА выразим синус угла АОА1:
sinАОА1 =
,
sinАОА1 =
, откуда АН = АО
sin
АОН =
.
Способ 4 (через теорему Пифагора).
Пусть А
Из по теореме Пифагора
.
Из по теореме Пифагора
.
Откуда 1 =
Тогда ,
.
Ответ:
№ 2. Метод параллельных прямых и плоскостей
Если точка А‘ находится вне участка плоскости α, указанного в задаче, то через точку А проводят прямую с, параллельную плоскости α, и выбирают на ней более
удобную точку С, проекция которой С‘ принадлежит данному участку
плоскости α. Длина отрезка СС‘ равна искомому расстоянию от точки А до
плоскости α. Либо можно через точку А провести плоскость, параллельную
плоскости α, и найти расстояние от произвольной точки этой плоскости до
плоскости α.
Задача № 2
Основанием прямой призмы является равнобедренный треугольник ABC, АВ = АС = 5, ВС = 6. Высота призмы равна 3. Найдите расстояние от середины ребра
до плоскости
.
Решение
Пусть высота треугольника
, тогда
середина стороны
.
Прямая параллельна плоскости
, поэтому расстояния от точек
и
до плоскости
равны.
Плоскость пересекает плоскость
по прямой
, где D — середина отрезка BC. Прямая BC перпендикулярна плоскости
поскольку перпендикулярна прямым
и
. Следовательно, плоскости
и
перпендикулярны. Поэтому расстояние от точки
до плоскости
равно высоте
прямоугольного треугольника
. Из условия следует, что
Отсюда
Ответ: 2,4
Задача № 3
В единичном кубе найти
расстояние от точки D до плоскости
Решение
- Так как плоскости
и
параллельны
() и D
, О1 – центр верхнего основания куба, то расстояние от точки D до плоскости
равно расстоянию от точки О1 до этой же плоскости.
- В плоскости АВ1С проведем прямую В1О, где О – центр нижнего
основания куба. Из точки О1 опустим перпендикуляр О1Е на эту прямую.
- Прямая О1Е лежит в плоскости ВВ1D1D, а прямая АС перпендикулярна
этой плоскости (АС BD), следовательно, О1Е
АС и О1Е
(
. Искомое расстояние – отрезок О1Е.
- В треугольнике ОВ1О1 (
О1 = 900) В1О1 =
(половина диагонали
квадрата), О1О = 1, ОВ1 =
. Откуда
.
Ответ: .
№ 3. Метод объемов
При нахождении расстояния от точки до плоскости искомое расстояние представляют как высоту подходящей треугольной пирамиды, так как при вычислении объема пирамиды можно в качестве основания выбрать любую ее грань. Объем пирамиды нужно выразить двумя способами по формуле , откуда
.
Задача № 4
В правильной треугольной призме
ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки А до плоскости ВСА1.
Решение
= АО, где АО
.
- Рассмотрим пирамиду АА1СВ с основанием АВС и основанием ВА1С.
Найдем объем пирамиды АА1СВ двумя способами:
,
, где А1А и АО – высоты пирамиды.
АВC – правильный, АА1 = 1, значит,
-
А1ВC – равнобедренный (А1В = А1С как диагонали граней призмы),
, где
высота
А1ВC,
=
,
AO =
.
Ответ: .
№ 4. Координатный метод
Расстояние от точки М ( до плоскости
, заданной уравнением
, можно вычислить по формуле
.
Для того, чтобы составить уравнение плоскости, необходимо знать координаты трех точек этой плоскости A (, B (
, C (
, не лежащих на одной прямой и подставить координаты этих точек в общее уравнение плоскости
. Затем решить систему уравнений
, найти числа
и составить уравнение плоскости.
- Соотношение отрезков в правильных многоугольниках (смотри выше)
Задача № 5
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найти расстояние от точки А до плоскости DEF1.
Решение
- Введем прямоугольную систему координат и найдем координаты точек
,
- Пусть
– уравнение плоскости DEF1. Подставим координаты точек
D, E, F1 в это уравнение, решим полученную систему уравнений:
Откуда . Следовательно, уравнение плоскости имеет вид
.
- Применим формулу и вычислим расстояние от точки до плоскости
Ответ: .
Полезные ссылки
- Расстояние от точки до плоскости. Решение задач с №7 по №11. Презентация.
- Расстояние от точки до плоскости. Решение задач с №8 по №11. Презентация.
- Расстояние от точки до плоскости. Решение задачи №13. Презентация.
- Расстояние от точки до плоскости. Решение задач №1,2. Презентация.
- Расстояние от точки до плоскости. Решение задач №10,11. Презентация.
- Расстояние от точки до плоскости, геометрические методы. Теория и задачи
- Расстояние от точки до плоскости. Решение задач С2.
- Онлайн тесты ЕГЭ
- Расстояния и углы в пространстве. Газета Математика, с.14.
- В. А. Смирнов. ЕГЭ 2010. Математика. Задачи С2. Геометрия. Стереометрия. Под редакцией А.Л.Семёнова, И.В.Ященко. Разработано МИОО. Москва. Издательство МЦНМО, 2010
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение расстояний от точки до прямой/плоскости
(blacktriangleright) Расстояние от точки до прямой/плоскости — длина перпендикуляра, опущенного из этой точки на прямую/плоскость.
(blacktriangleright) Т.к. все точки одной из параллельных прямых находятся на одинаковом расстоянии от другой прямой, то расстояние между параллельными прямыми — это длина перпендикуляра, опущенного из любой точки одной прямой ко второй прямой.
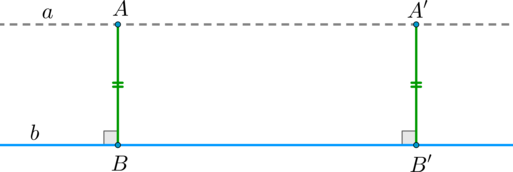
Таким образом, иногда бывает удобно искать расстояние между точкой (A) и прямой (b) как расстояние между прямой (a (aparallel b,
asubset A)) и прямой (b) (то есть опускать перпендикуляр не из точки (A), а из какой-нибудь другой “более удобной” точки на прямой (a)).
(blacktriangleright) Т.к. все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости, то расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости к другой плоскости.
(blacktriangleright) Т.к. все точки прямой, параллельной плоскости, находятся на одинаковом расстоянии от этой плоскости, то расстояние между параллельными прямой и плоскостью — это длина перпендикуляра, опущенного из любой точки прямой к плоскости.
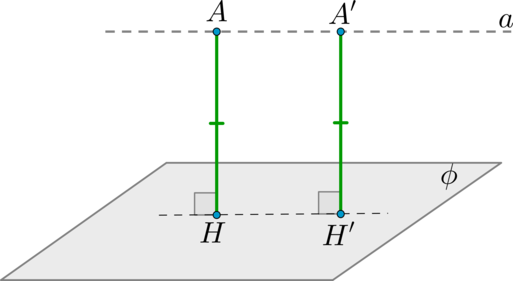
Таким образом, иногда бывает удобно искать расстояние между точкой (A) и плоскостью (phi) как расстояние между прямой (a (aparallel
phi, asubset A)) и плоскостью (phi) (то есть опускать перпендикуляр не из точки (A), а из какой-нибудь другой “более удобной” точки на прямой (a)).
Задание
1
#6927
Уровень задания: Легче ЕГЭ
Дана треугольная пирамида (SABC), причем грани (SAB) и (SAC) представляют собой равные равнобедренные треугольники с прямыми углами при вершине (A). Найдите расстояние от точки (A) до грани (SBC), если высота пирамиды равна (h) и равна (BC).
Из условия задачи следует, что:
1) (SAperp AB, AC Rightarrow SAperp (ABC));
2) (SA=AB=AC=h=BC);
3) (SB=SC=hsqrt2).
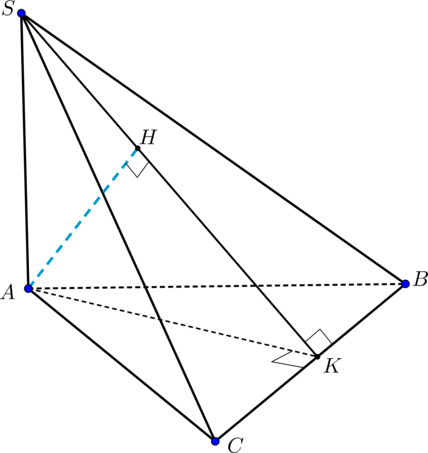
Т.к. (triangle BAC) равнобедренный, то (AKperp BC, K) – середина (BC). Аналогично, (SKperp BC). Таким образом, перпендикуляр (AH) на плоскость (SBC) упадет на прямую (SK) (удовлетворяет теореме о трех перпендикулярах: (HK) – проекция, (AK) – наклонная, обе перпендикулярны (BC)).
По теореме Пифагора (AK=dfrac{hsqrt3}{2}).
Следовательно, (mathrm{tg}, angle
SKA=dfrac{SA}{AK}=dfrac{2sqrt3}{3}=dfrac{AH}{HK}).
Значит, (AH=2sqrt3x, HK=3x).
По теореме Пифагора из (triangle AHK) находим (x=dfrac{1}{2sqrt7}h Rightarrow AH=sqrt{dfrac{3}{7}}h)
Ответ:
(sqrt{dfrac{3}{7}}h)
Задание
2
#3143
Уровень задания: Сложнее ЕГЭ
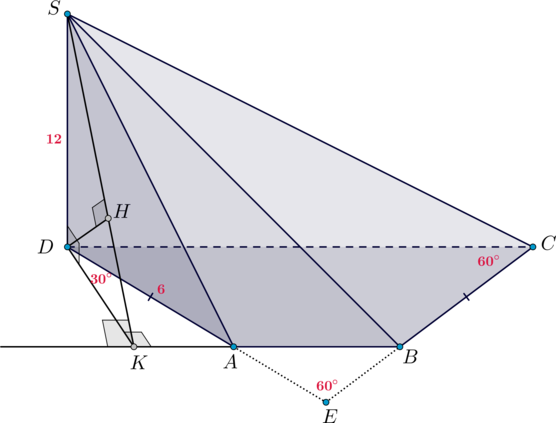
В основании четырехугольной пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), причем (AD=BC=6), (CD>AB). Угол между прямыми (AD) и (BC) равен (60^circ). Известно, что (SD=12) – высота пирамиды.
Найдите расстояние от точки (C) до грани (SAB).
Так как (CDparallel AB) – основания трапеции, то (CD) параллельна плоскости (SAB), в которой находится прямая (AB). Следовательно, расстояние от любой точки прямой (CD) до плоскости (SAB) будет одинаковым. Найдем расстояние до плоскости (SAB) от точки (D).
Так как (SD) – высота пирамиды, то (SDperp (ABC)). Проведем (DKperp AB) (точка (K) упадет на продолжение отрезка (AB) за точку (A)).
Если (E) – точка пересечения прямых (AD) и (BC), то (angle
AEB=60^circ). Так как также (angle BAE=angle ABE) (так как трапеция равнобедренная), то (triangle AEB) равносторонний и (angle BAE=60^circ). Следовательно, и (angle ADC=angle
BCD=60^circ).
По теореме о трех перпендикулярах (SKperp AB) (заметим, что (SKin
(SAB))). Тогда перпендикуляр (DH) из точки (D) на плоскость (SAB) упадет на (SK) (в противном случае по теореме о трех перпендикулярах проекция (HK) наклонной (DK) будет перпендикулярна (AB) и тогда будут существовать в одной плоскости два перпендикуляра (SK) и (HK) к прямой (AB), что невозможно).
Таким образом, необходимо найти (DH).
Из прямоугольного треугольника (DAK) [cos angle ADK=cos 30^circ=dfrac{DK}{DA} quadRightarrowquad
DK=3sqrt3.] Тогда по теореме Пифагора из (triangle SDK): [SK=sqrt{SD^2+DK^2}=sqrt{144+27}=3sqrt{19}] Тогда из этого же треугольника [DKcdot SD=DHcdot SK quadRightarrowquad DH=dfrac{12sqrt3}{sqrt{19}}.]
Ответ:
(dfrac{12sqrt3}{sqrt{19}})
Задание
3
#1248
Уровень задания: Сложнее ЕГЭ
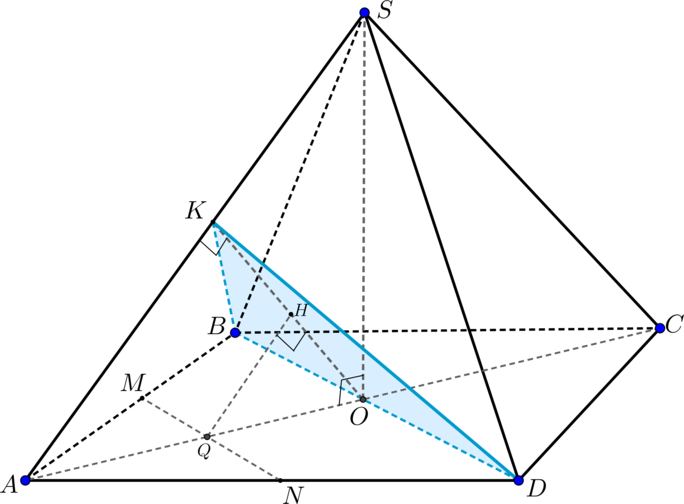
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S). Через точку пересечения диагоналей основания провели плоскость (alpha) перпендикулярно ребру (SA). Найдите расстояние от точки (N) до плоскости (alpha), если (N) – середина (AD=2sqrt2), а высота пирамиды равна (11).
1) Построим сечение пирамиды плоскостью (alpha). Т.к. (alphaperp
SA), то (SA) перпендикулярна двум пересекающимся прямым, лежащим в (alpha). Обозначим (ACcap BD=O). Проведем (OKperp SA).
По теореме о трех перпендикулярах (SAperp BD) как наклонная ((SOperp (ABC), OAperp BD) – проекция).
Таким образом, имеем две пересекающиеся прямые (OK) и (BD) из плоскости (alpha). Значит, сечением является треугольник (BKD).
2)Проведем (MNparallel BD), следовательно, (MNparallel alpha). Т.к. расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то (rho(N, alpha)=rho(Q, alpha)) ((rho) — расстояние).
Т.к. по условию (SAperp alpha), то проведем (QHparallel SA
Rightarrow QHperp alpha).
По построению (MN) – средняя линия (triangle BAD), следовательно, (AQ=QO Rightarrow QH) – средняя линия (triangle KAO Rightarrow
QH=dfrac{1}{2}AK).
Рассмотрим (triangle SAO):
(AO=2).
Из (triangle AKO sim triangle ASO Rightarrow
dfrac{AK}{AO}=dfrac{AO}{AS} Rightarrow AK=dfrac{4sqrt5}{25}
Rightarrow QH=dfrac{2sqrt5}{25}).
Ответ:
(dfrac{2sqrt5}{25})
Задание
4
#3195
Уровень задания: Сложнее ЕГЭ
В правильной треугольной призме (ABCA_1B_1C_1) стороны основания равны (6), боковые ребра равны (8), точка (D) – середина (CC_1). Найдите расстояние от вершины (B) до плоскости (AB_1D).
(Задача от подписчиков)
Найдем расстояние от точки (B) до плоскости (AB_1D) через объем пирамиды (BAB_1D).
Так как призма правильная, то боковые грани – равные прямоугольники. Следовательно, так как (CD=DC_1), то (triangle
ACD=triangle B_1C_1D), откуда (AD=DB_1). Следовательно, если (O) – точка пересечения диагоналей (AB_1) и (A_1B), то (DOperp AB_1) (медиана и высота в равнобедренном треугольнике).
Пусть (K) – середина (AB). Тогда (CKparallel DO). Значит, так как (CKperp AB), то (DOperp AB). Отсюда (DO) перпендикулярна двум пересекающимся прямым (AB_1) и (AB) в плоскости (ABB_1), следовательно, (DOperp(ABB_1)). Значит, (DO) – высота пирамиды (BAB_1D) к основанию (ABB_1).
Следовательно, [dfrac 13cdot DOcdot S_{ABB_1}=V_{BAB_1D}=dfrac 13cdot hcdot
S_{AB_1D},] где (h) – расстояние от точки (B) до ((AB_1D)).
1) (S_{ABB_1}=0,5cdot ABcdot BB_1=0,5cdot 6cdot 
2) (DO=CK) как противоположные стороны параллелограмма (DOKC) ((DOparallel CK), (DCparallel OK)).
3) (CK=0,5sqrt3AB=3sqrt3).
4) (AB_1=sqrt{AB^2+BB_1^2}=10).
5) (S_{AB_1D}=0,5cdot DOcdot AB_1=0,5cdot 3sqrt3cdot 10).
Следовательно: [h=dfrac{3sqrt3cdot 0,5cdot 6cdot 8}{0,5cdot 3sqrt3cdot 10}=4,8]
Ответ: 4,8
Задание
5
#1250
Уровень задания: Сложнее ЕГЭ
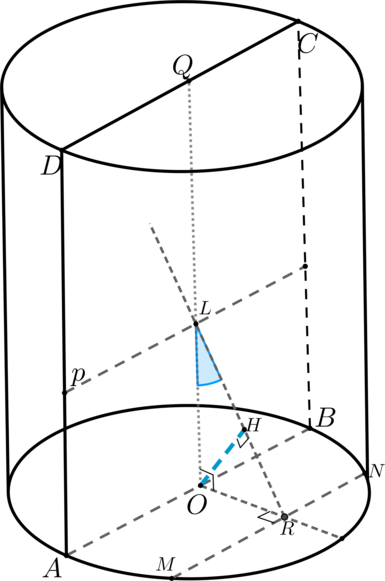
В цилиндре параллельно диаметру (AB=10) в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках (M) и (N), причем (MN=6). Через отрезок (MN) проведена плоскость (alpha) под углом (15^o) к плоскости осевого сечения (ABCD). Найдите расстояние от центра нижнего основания до плоскости (alpha).
1) Т.к. (MNparallel AB), то плоскость (alpha) пересечет плоскость (ABCD) по прямой (p), параллельной (AB) (если это не так, то (pcap
AB = K Rightarrow Kin text{нижнему основанию и } Kin alpha
Rightarrow K in MN Rightarrow ABcap MN ne varnothing), что противоречит условию).
Обозначим за (OQ) – ось цилиндра. Тогда (OQperp AB Rightarrow
OQperp p) ((OQcap p =L)). Проведем (ORperp MN Rightarrow ) по теореме о трех перпендикулярах (RLperp MN Rightarrow RLperp p
Rightarrow angle RLO) – угол между плоскостями (ABCD) и (alpha).
2) Т.к. (ORperp MN text{ и } LRperp MN), то перпендикуляр из точки (O) на плоскость (alpha) упадет на прямую (LR).
Рассмотрим (triangle OMR: OM=5, MR=3, angle ORM=90^circ
Rightarrow OR=4).
Рассмотрим (triangle LOR: angle HOR=angle RLO=15^circ
Rightarrow OH=ORcdot cos15^circ=4cdot
cos{(45^circ-30^circ)}=sqrt6+sqrt2).
Ответ:
(sqrt6+sqrt2).
Задание
6
#1249
Уровень задания: Сложнее ЕГЭ
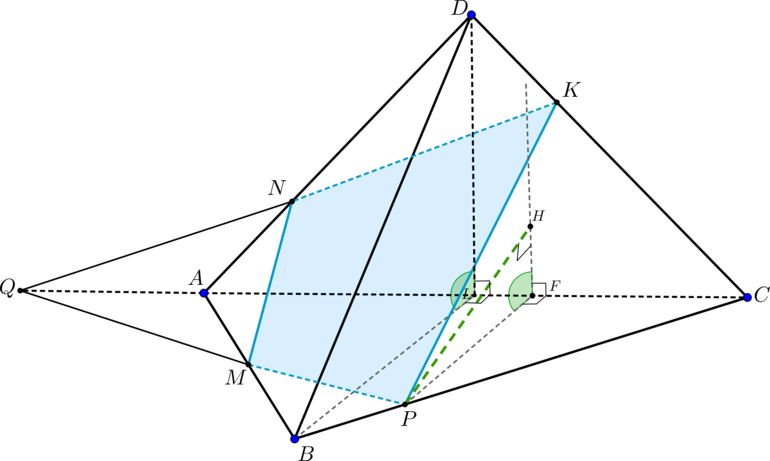
(ABCD) – правильный тетраэдр с ребром (6). (M, N, K) – такие точки на ребрах (AB, AD, CD) соответственно, что (AM=MB, DN=2NA=CK). Плоскость (MNK) пересекает ребро (BC) в точке (P). Найдите расстояние от точки (P) до плоскости (ACD).
1) По условию (ABCD) представляет собой правильную треугольную пирамиду, все ребра которой равны (6). Найдем, в каком отношении точка(P) делит отрезок (BC). Для этого построим сечение пирамиды плоскостью (MNK). Продлим прямую (NK) до пересечения с прямой (AC) – получим точку (Q). Соединив точки (Q) и (M), получим линию пересечения основания – отрезок (MP) (сечением является четырехугольник (MNKP)).
По теореме Менелая для (triangle ADC) и прямой (QK) имеем:
(dfrac{AN}{ND}cdot dfrac{DK}{KC}cdot dfrac{CQ}{QA}=1
Rightarrow QA=2).
Аналогично для (triangle ABC) и прямой (QP):
(dfrac{BM}{MA}cdot dfrac{AQ}{QC}cdot dfrac{CP}{PB}=1
Rightarrow BP=dfrac{6}{5}).
2) Проведем (PHperp ADC) и (PFperp AC). Тогда по теореме о трех перпендикулярах (HFperp AC), следовательно, (angle HFP=angle
(ABC, ACD)=angle alpha). Найдем (PH) из треугольника (PHF). Для этого найдем (PF) и (angle alpha).
Проведем (BLperp AC), тогда (angle BLD=angle alpha). Треугольник (BLD) – равнобедренный ((BL=LD=3sqrt3, BD=6)). По теореме косинусов найдем (cos angle alpha=dfrac{1}{3})
Тогда (sin angle alpha = dfrac{2sqrt2}{3}=dfrac{PH}{PF}).
(triangle BLC sim triangle PFC Rightarrow
PF=dfrac{12sqrt3}{5})
Таким образом, (PH=dfrac{8sqrt{6}}{5}).
Ответ:
(dfrac{8sqrt{6}}{5}).
Задания, предлагающие школьнику найти расстояние от точки до прямой, в ЕГЭ встречаются ежегодно. При этом умение выполнять подобные задачи требуется выпускникам, сдающим как базовый уровень экзамена по математике, так и профильный. Научившись находить расстояние от точки до плоскости, в ЕГЭ школьник сможет правильно выполнить задание и получить заветные баллы.
«Прокачать» навыки и улучшить знания в таком непростом разделе геометрии, как стереометрия, вам поможет наш образовательный проект. «Школково» предлагает учащимся и их преподавателям по-новому выстроить процесс подготовки к сдаче единого госэкзамена.
Для того чтобы вы могли во время ЕГЭ правильно и с минимальными временными затратами решать задачи, где требуется найти расстояние от точки до прямой, мы предлагаем прежде всего повторить определения и основные правила. Для этого достаточно посетить раздел «Теоретическая справка». Здесь мы разместили материал, составленный нашими специалистами специально для учащихся с различным уровнем подготовки.
Затем для закрепления полученных знаний и отработки навыков выполните задания на нахождение расстояния от точки до плоскости в ЕГЭ; вы можете это сделать вне зависимости от того, где вы находитесь: в Москве или другом городе. Богатая подборка задач представлена в разделе «Каталог».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ЕГЭ Профиль №13. Расстояние от точки до прямой. Расстояние от точки до плоскости
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Расстояние от точки до прямой. Расстояние от точки до плоскости
Расстояние от точки до прямой. Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую. Расстояние от точки до прямой можно вычислить, как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот. При этом если длины сторон треугольника все разные a, b, c (треугольник не равносторонний и не равнобедренный), то высоту треугольника, например, к стороне a можно искать по следующему алгоритму: 1) по теореме косинусов находим косинус угла между сторонами a и b; 2) зная косинус этого угла, используя основное тригонометрическое тождество, найти его синус; 3) синус найденного угла есть отношение искомой высоты к стороне b. В прямоугольном треугольнике высота к гипотенузе равна произведению катетов, деленному на гипотенузу.
Расстояние от точки до плоскости. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость. Расстояние от точки M до плоскости α: 1) равно расстоянию до плоскости α от произвольной точки P, лежащей на прямой l, которая проходит через точку M и параллельна плоскости α; 2) равно расстоянию до плоскости α от произвольной точки P, лежащей на плоскости α, которая проходит через точку M и параллельна плоскости α. Метод объемов: Если объем пирамиды ABCS равен ({V_{ABCS}}), то расстояние от точки S до плоскости ABC можно найти используя формулу объема пирамиды: ({V_{ABCS}} = frac{1}{3}{S_{ABC}} cdot H), где H – расстояние от точки S до плоскости ABC.
Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра. Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра, которое равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
1В. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной (AB = 4) и диагональю (BD = 7). Все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребре AS – точка F так, что (SF = BE = 3.)
а) Докажите, что плоскость CEF параллельна ребру SB.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
ОТВЕТ: (frac{{2sqrt {15} }}{7}).
2В. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а высота призмы равна 2. На ребрах B1C1 и AB отмечены точки P и Q соответственно, причем (P{C_1} = 3,quad AQ = 4.) Плоскость A1PQ пересекает ребро BC в точке М.
а) Докажите, что точка М является серединой ребра BC.
б) Найдите расстояние от точки B до плоскости A1PQ.
ОТВЕТ: (frac{{3sqrt {30} }}{5}).
3В. На ребрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причем (DP = 4,;;{B_1}Q = 3.) Плоскость APQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СC1.
б) Найдите расстояние от точки С до плоскости APQ.
ОТВЕТ: (frac{{12sqrt {26} }}{{13}}).
4В. В основании прямой треугольной призмы ABCA1B1C1 лежит прямоугольный треугольник ABC с прямым углом С, (AC = 4,;;BC = 16,) (A{A_1} = 4sqrt 2 .) Точка Q – середина ребра A1B1, а точка P делит ребро B1C1 в отношении 1 : 2, считая от вершины С1. Плоскость APQ пересекает ребро СС1 в точке М.
а) Докажите, что точка М является серединой ребра СC1.
б) Найдите расстояние от точки А1 до плоскости APQ.
ОТВЕТ: (frac{{32sqrt {57} }}{{57}}).
5В. В правильной четырехугольной призме ABCDA1B1C1D1 сторона АВ основания равна 8, а боковое ребро AA1 равно (4sqrt 2 ). На ребрах BC и С1D1 отмечены точки K и L соответственно, причем (BK = {C_1}L = 2.) Плоскость (alpha ) параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A1C перпендикулярна плоскости (alpha ).
б) Найдите расстояние от точки B до плоскости (alpha ).
ОТВЕТ: (frac{{2sqrt {10} }}{5}).
6В. В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а боковое ребро АА1 равно (3sqrt 6 ). На ребрах АВ и В1С1 отмечены точки К и L соответственно, причем (AK = 2,;;{B_1}L = 4.) Точка М – середина ребра А1С1. Плоскость (alpha ) параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости (alpha ).
б) Найдите расстояние от точки С до плоскости (alpha ).
7В. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что (PA = AQ = RC = 2).
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от точки D до плоскости PQR.
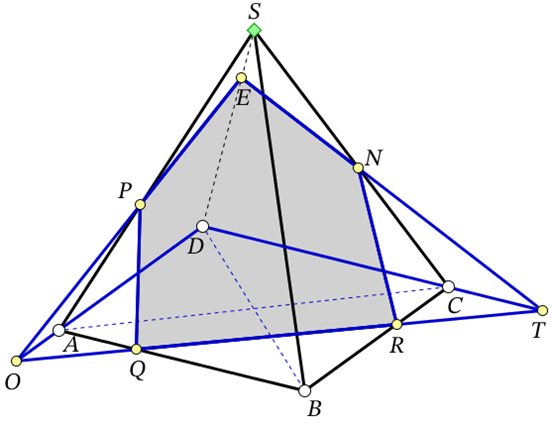
(frac{{BQ}}{{QA}} = frac{{BR}}{{RC}},,,, Rightarrow ,,,,QRparallel AC,) но (AC bot BD,) тогда (DB bot QR.) Следовательно, (SD bot QR) по теореме о трёх перпендикулярах.
(left. {begin{array}{*{20}{c}}{SD bot QR}\{SD bot PQ}end{array}} right},,, Rightarrow ,,,,SD bot PQR.)
б) Искомое расстояние DE. Треугольник SEP прямоугольный с гипотенузой SP и (angle PSE = {60^ circ }.) Тогда (cos {60^ circ } = frac{{SE}}{{SP}},,,, Leftrightarrow ,,,,SE = frac{3}{2}) и (DE = DS — SE = 5 — frac{3}{2} = frac{7}{2}.)
Ответ: (frac{7}{2}.)
8В. В правильной треугольной пирамиде SABC сторона основания AB равна 30, а боковое ребро SA равно 28. Точки M и N – середины ребер SA и SB соответственно. Плоскость (alpha ) содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость (alpha ) делит медиану CE основания в отношении 5 : 1, считая от точки С.
б) Найдите расстояние от точки А до плоскости (alpha ).
ОТВЕТ: (frac{{5sqrt 3 }}{2}).
9В. В правильной четырёхугольной призме ABCDA1B1C1D1 основание ABCD — квадрат. Точка M — центр боковой грани BCC1B1.
а) Докажите, что плоскость A1D1M делит диагональ AC1 в отношении 2 : 1, считая от точки A.
б) Найдите расстояние от точки M до прямой BD1, если сторона основания призмы равна 6, а боковое ребро равно 3.
10В. Дана треугольная призма ABCA1B1C1 с основаниями ABC и A1B1C1. Точка M — центр боковой грани BCC1B1.
а) Постройте точку пересечения прямой A1M с плоскостью ABC.
б) Найдите расстояние от точки M до прямой AB1, если призма прямая, ABC — прямоугольный треугольник с прямым углом C, а диагонали боковых граней AA1B1B и BB1C1C равны 17 и 15 соответственно.
11В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1.
а) Докажите, что плоскость CA1F1 делит ребро BB1 пополам.
б) Найдите расстояние от точки C до прямой A1F1, если стороны основания призмы равны 5, а боковые рёбра равны 11.
12В. Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость α, проходящая через ребро AB и середину ребра SE, делит ребро SC в отношении 2 : 1, считая от вершины S.
б) Найдите расстояние от точки S до плоскости α, если сторона основания пирамиды равна (2sqrt 3 ), а угол между боковой гранью и плоскостью основания пирамиды равен 60º.
13В. Основание пирамиды DABC — прямоугольный треугольник ABC с прямым углом C. Высота пирамиды проходит через середину ребра AC, а боковая грань ACD — равносторонний треугольник.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра AD, — прямоугольный треугольник.
б) Найдите расстояние от вершины D до этой плоскости, если M — середина ребра AD, а высота пирамиды равна 6.
14В. Основание пирамиды SABCD — прямоугольник ABCD. Высота SH пирамиды лежит в плоскости CSD.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра SA, отличную от S и A, — прямоугольная трапеция.
б) Найдите расстояние от вершины S до этой плоскости, если H — середина ребра CD, M — середина ребра SA, (SC = CD,;;SH = 2sqrt 3 ).
15В. Основание пирамиды SABCD — квадрат ABCD. Боковое ребро SD перпендикулярно плоскости основания. Точка M — середина высоты пирамиды.
а) Докажите, что прямая SB параллельна плоскости ACM.
б) Найдите расстояние от точки B до плоскости ACM, если (AB = 
16В. Основание пирамиды SABCD — прямоугольник ABCD. Боковое ребро SD перпендикулярно плоскости основания.
а) Докажите, что прямые SC и AD перпендикулярны.
б) Пусть M — середина высоты пирамиды. Найдите расстояние от точки B до плоскости ACM, если AB = 8, BC = 6, а синус угла между плоскостью ACM и плоскостью основания пирамиды равен 5/6.
17В. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Высота пирамиды втрое больше стороны основания и проходит через точку E.
а) Докажите, что угол между боковой гранью ASB и плоскостью основания равен 60º.
б) Найдите расстояние от точки C до плоскости ASB, если сторона основания пирамиды равна 4.
18В. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF c центром O. Отрезок OA1 — высота призмы.
а) Докажите, что плоскость FF1E перпендикулярна плоскости основания призмы.
б) Найдите расстояние от точки A до плоскости BCC1, если сторона основания призмы равна (2sqrt 3 ).
19В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1.
а) Докажите, что плоскость ADC1 перпендикулярна плоскости FBB1.
б) Найдите расстояние от точки C до плоскости ADC1, если AA1 = 4, а косинус угла между прямой AC1 и плоскостью ABC равен (frac{3}{{sqrt {13} }}).
20В. Дана правильная четырёхугольная призма ABCDA1B1C1D1 со стороной основания (sqrt 2 ) и боковым ребром 2. Точки M и N — середины рёбер A1B1 и CC1 соответственно.
а) Докажите, что MN ⊥ BC1.
б) Найдите расстояние от точки M до плоскости BC1D.
ОТВЕТ: (frac{{3sqrt 5 }}{5}).
21В. Основание пирамиды SABCD — равнобедренная трапеция ABCD с основаниями AD и BC, причём AD = 2BC = 2AB. Высота SH пирамиды проходит через точку пересечения прямых AB и CD.
а) Докажите, что треугольник SBD прямоугольный.
б) Найдите расстояние от точки C до плоскости ASD, если SH = BC = 4.
22В. Основание пирамиды SABCD — прямоугольная трапеция ABCD с большим основанием AD и прямым углом D. Высота SH пирамиды проходит через точку пересечения прямых AB и CD.
а) Докажите, что грань ASD — прямоугольный треугольник.
б) Найдите расстояние от точки B до плоскости ASD, если AD = 3BC = 3, ∠BAD = 45º и SH = 4.
23В. Боковые рёбра пирамиды SABC с вершиной S попарно перпендикулярны.
а) Докажите, что высота SH пирамиды проходит через точку пересечения высот основания ABC.
б) Найдите SH, если боковые рёбра равны 2, 2 и (7sqrt 2 ).
24В. Боковые рёбра пирамиды SABC с вершиной S попарно перпендикулярны, M — произвольная точка на ребре BC.
а) Докажите, что плоскости AMS и BSC перпендикулярны.
б) Высота SH пирамиды равна 12. Прямая AH пересекает ребро BC в точке K. Найдите расстояние от точки K до прямой AS, если AS = 20.
25В. Плоскость проходит через середины боковых рёбер DA и DC треугольной пирамиды DABC и точку пересечения медиан основания ABC.
а) Постройте точку пересечения этой плоскости с прямой DB.
б) Найдите расстояние от точки A до этой плоскости, если все рёбра пирамиды равны (3sqrt 6 ).
26В. Плоскость проходит через середины сторон AD и BC основания ABCD правильной четырёхугольной пирамиды SABCD и точку пересечения медиан боковой грани CSD.
а) Постройте точку пересечения прямой AS с этой плоскостью.
б) Найдите расстояние от точки B до этой плоскости, если все рёбра пирамиды равны (2sqrt 3 ).
27В. Все грани параллелепипеда ABCDA1B1C1D1 — равные ромбы, причём плоские углы при вершине C острые.
а) Докажите, что AA1 ⊥ BD.
б) Найдите расстояние от вершины C до плоскости A1B1C1, если плоские углы при вершине C равны 60°, а (A{A_1} = sqrt 6 ).
28В. Основание наклонной призмы ABCA1B1C1 — равносторонний треугольник ABC. Боковые грани AA1B1B и AA1C1C — равные ромбы с острым углом при общей вершине A.
а) Докажите, что боковая грань BB1C1C — квадрат.
б) Найдите расстояние от вершины A до плоскости BB1C1, если ∠CAA1 = 60°, а сторона основания призмы равна (sqrt 2 ).
29В. Основание пирамиды SABCD — параллелограмм ABCD. Боковые рёбра SA и SD равны. Точка M лежит на боковом ребре SC и не совпадает с его концами. Плоскость α проходит через точку M параллельно прямым BC и SA.
а) Докажите, что сечение пирамиды плоскостью α — равнобедренная трапеция.
б) Найдите расстояние от точки A до плоскости α, если боковая сторона этой трапеции равна меньшему основанию, а все рёбра пирамиды равны 1.
ОТВЕТ: (frac{{sqrt 6 }}{6}).
30В. Точка K лежит на стороне AB основания ABCD правильной четырёхугольной пирамиды SABCD, все рёбра которой равны. Плоскость α проходит через точку K параллельно плоскости ASD. Сечение пирамиды плоскостью α — четырёхугольник, в который можно вписать окружность.
а) Докажите, что BK = 2AK.
б) Найдите расстояние от вершины S до плоскости α, если все рёбра пирамиды равны 1.
ОТВЕТ: (frac{{sqrt 6 }}{9}).
31В. В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM = DN = 4 и AK = 3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки K до плоскости SBC.
ОТВЕТ: (frac{{12sqrt 5 }}{5}).
32В. ABCA1B1C1 — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.
а) Докажите что периметр сечения призмы плоскостью α больше 40.
б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.
ОТВЕТ: (frac{{24sqrt {273}}}{91}).
33В. Точка O — центр основания ABCDEF правильной шестиугольной пирамиды SABCDEF. Точки K, L, M, T — середины отрезков AF, SF, SD, MK соответственно.
а) Докажите, что точка T лежит на отрезке LO.
б) Найдите CT, если сторона основания пирамиды равна 4, а высота пирамиды равна 48.
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
План урока:
Понятие перпендикуляра
Расстояния между плоскостями и прямыми
Теорема о трех перпендикулярах
Угол между прямой и плоскостью
Задачи на перпендикуляры, наклонные, расстояния
Понятие перпендикуляра
Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:
Запомним некоторые геометрические термины. В таком построении:
- отрезок МН – это наклонная;
- отрезок НК – это проекция наклонной, или просто проекция;
- К – основание перпендикуляра;
- Н – основание наклонной.
Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).
Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.
Расстояния между плоскостями и прямыми
Докажем довольно очевидный факт:
Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:
Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.
Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.
Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.
Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.
Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:
Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.
Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.
Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.
Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.
Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:
Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:
Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.
Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.
Далее через K в плоскости γ проведем прямую р’, параллельную р:
Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:
В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.
Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.
Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).
Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.
Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.
Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.
Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.
Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:
Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.
Итак, из всех наших рассуждений мы можем сделать следующие выводы:
Теорема о трех перпендикулярах
Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.
Проиллюстрируем теорему с помощью картинки:
Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.
Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):
Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.
Угол между прямой и плоскостью
Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.
Пусть надо определить угол между прямой HM и плоскостью α:
Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.
Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:
Задачи на перпендикуляры, наклонные, расстояния
Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.
Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:
Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.
Ответ: 1.
Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.
Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:
Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:
Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.
Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.
Найти АК можно с помощью тригонометрии в ∆АКD:
Задание. Найдите расстояние от H до плоскости EDG:
Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:
Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.
В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.
Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.
Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.
Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.
Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:
Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:
Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:
Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:
Задание. Найдите расстояние между прямыми ВС и DH:
Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.
Ответ: 1.
Задание. Каково расстояние между прямыми ВС и DG:
Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:
Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.
Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:
Задание. Найдите расстояние между ребрами АВ и HG:
Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.
Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:
Задание. Чему равно расстояние между ребром AB и диагональю FD:
Решение. Пусть А1, D1, H1 и Е1 – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А1, D1, H1 плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:
Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.
Заметим, что в четырехугольнике АА1D1D стороны АА1 и DD1 параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА1D1D – параллелограмм. Более того, раз у него есть прямые углы ∠А1АDи ∠АDD1, то можно утверждать, что АА1D1D – прямоугольник. Тогда АD||A1D1. Аналогично можно показать, что DHH1D1 – прямоугольник, и DH||D1H1.
Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А1D1и D1H1, а в плоскости ADH находятся прямые AD и DH, и АD||A1D1, и DH||D1H1, то по этому признаку α||ADH.
Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD1. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A1D1и D1H1 в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.
Отсюда вытекает, что α должна проходить через середину Е1. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА1, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е1.
Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е1D1. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:
Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е1FD = ∠D1DF (накрест лежащие углы при секущей FD). ∠FKE1 и ∠DKD1 одинаковы уже как вертикальные углы. Тогда ∆FKE1 и ∆DKD1 подобны по 2 углам. Но отрезки FE1 и DD1 одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE1 и ∆DKD1 равны, и поэтому Е1К = KD1. Это и значит, что К – середина Е1D1.
Также отметим, что Е1D1 – диагональ в четырехугольнике А1Е1Н1D1. Докажем, что А1Е1Н1D – это квадрат. Ранее мы уже показали, что АА1D1D и DHH1D1 – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА1Е1Е и ЕЕ1Н1Н. Из этого вытекает равенство сторон:
То есть в А1Е1Н1D1 все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А1D1H1. AD⊥CDHG и AD||A1D1, поэтому А1D1⊥CDHG. Значит, также А1D перпендикулярна любой прямой на грани CDHG, в том числе и D1H1. То есть ∠А1D1H1 = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.
Итак, мы выяснили, что А1Е1Н1D1 – квадрат, а К – середина его диагонали Е1D1. Получается, что К – точка пересечения диагоналей квадрата А1Е1Н1D1, ведь эта точка пересечения как раз делит диагонали пополам.
Теперь мы можем наконец доказать, что А1К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А1К принадлежит α, то А1К⊥АВ. Но как же доказать, что А1К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е1К – это проекция FK на α, и Е1К⊥А1К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А1К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А1К⊥FK.
Осталось лишь вычислить длину А1К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А1Е1К, в котором ∠А1Е1К = 45°:
Отвлечемся от куба и рассмотрим другую задачу.
Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?
Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть
Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:
Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.
Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.
Задание. Найдите угол между ребром куба BD и гранью СDHG:
Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:
Ответ: 45°.
Задание. Вычислите угол между ребром CD и плоскостью BDHF:
Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:
Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.
Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.
Ответ: 45°
Задание. Чему равен угол между прямой BD и плоскостью ABGH:
Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:
Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.
В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.
ВD найдем из прямоугольного ∆ABD:
Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:
По таблице синусов легко определить, что ∠DBK = 30°.
Ответ: 30°.
В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.
Расстояние от точки до прямой в пространстве.
Навигация по странице:
- Определение расстояния от точки до прямой в пространстве
- Формула для вычисления расстояния от точки до прямой в пространстве
- Вывод формулы вычисления расстояния от точки до прямой в пространстве
- Примеры задач на вычисление расстояния от точки до прямой в пространстве
Определение.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Формула для вычисления расстояния от точки до прямой в пространстве
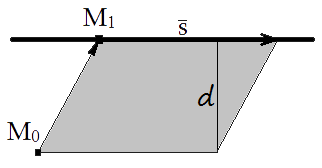
Если s = {m; n; p} — направляющий вектор прямой l, M1(x1, y1, z1) — точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу
Вывод формулы вычисления расстояния от точки до прямой в пространстве
Если задано уравнение прямой l то несложно найти s = {m; n; p} — направляющий вектор прямой и M1(x1, y1, z1) — координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах
S = |M0M1×s|.
С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне
S = |s|d.
В нашем случае высота будет равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s.
Приравняв площади несложно получить формулу расстояния от точки до прямой.
Примеры задач на вычисление расстояния от точки до прямой в пространстве
Пример 1.
Найти расстояние между точкой M(0, 2, 3) и прямой
| x — 3 | = | y — 1 | = | z + 1 |
| 2 | 1 | 2 |
Решение.
Из уравнения прямой получим:
s = {2; 1; 2} — направляющий вектор прямой;
M1(3; 1; -1) — точка лежащая на прямой.
Тогда
M0M1 = {3 — 0; 1 — 2; -1 — 3} = {3; -1; -4}
| M0M1×s = | i | j | k | = |
| 3 | -1 | -4 | ||
| 2 | 1 | 2 |
= i ((-1)·2 — (-4)·1) — j (3·2 — (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}
d =
|M0M1×s||s|
=
√22 + (-14)2 + 52√22 + 12 + 22
=
√225√9
=
153
= 5
Ответ: расстояние от точки до прямой равно 5.