Распределенность терминов в суждениях
Объединяя
количественную и качественную
характеристики, суждения делятся на:
-
общеутвердительные
(А)
— «Все S есть Р», -
частноутвердительные
(I)
— «Некоторые S есть Р», -
общеотрицательные
(Е)
— «Ни один S не есть Р», -
частноотрицательные
(О)
— «Некоторые S не есть Р»
В
Средние века были приняты эти буквенные
обозначения по первым гласным латинских
слов
affirmo
— утверждаю и nego
— отрицаю.
Термин
считается распределенным
(обозначается»+»), если он взят в
полном объеме. Термин считается
нераспределенным
(обозначается»-«), если он взят в
части объема.
Суждение
А: Общеутвердительное
«Все студенты
нашей группы сдали зачет по логике»
Суждение
I: Частноутвердительное
«Некоторые
студенты сдали зачет»
Суждение
Е: Общеотрицательное
«Ни один студент
не сдал зачет»
Суждение
О: Частноотрицательное
«Некоторые
студенты не сдали зачет»
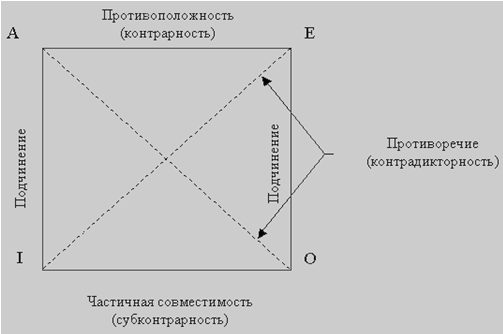
3. Отношения между простыми суждениями. Логический квадрат.
Несравнимыми
среди простых суждений являются суждения,
имеющие различные субъекты или предикаты.
Сравнимыми
являются суждения с одинаковыми
субъектами и предикатами.
Для иллюстрации отношений между простыми
суждениями используется логический
квадрат:
Среди
сравнимых различают совместимые
суждения, которые могут быть одновременно
истинными, и несовместимые
суждения, которые одновременно истинными
быть не могут.
Совместимость
бывает трех видов: полная
совместимость (эквивалентность);
подчинение; частичная совместимость
(субконтрарность).
Несовместимость бывает
двух видов: противоположность
(контрарность) и противоречивость
(контрадикторность).
I. Отношением подчинения связаны
суждения А и I, Е и О. Общие суждения (А и
Е) являются подчиняющими, а частные (I,
О) подчиненными. Для суждений находящихся
в отношении подчинения, имеет значение
условие истинности: Если истинно А(Е),
то истинно и I(O), но не наоборот.
II.
Отношением противоречия связаны суждения
Е и I, А и О. Два противоречивых суждения
(согласно законам логики) не могут быть
одновременно ни истинными, ни ложными
Если А — истинно, то О — ложно
Если А —
ложно, то О — истинно
Если О — истинно,
то А — ложно
Если О — ложно, то А —
истинно
Если Е —
истинно, то I — ложно
Если
Е — ложно, то I — истинно
Если
I -истинно, то E — ложно
Если
I — ложно, то E — истинно
III. Отношением
контрарности (противоположности) связаны
только общие суждение А и Е. Закон
исключения третьего к таким суждениям
не применим. А и Е могут оказаться
одновременно ложными, но не могут быть
одновременно истинными (пример: оба
суждения «Все любят логику» и «никто
не любит логику» — ложны).
IV.
Отношение субконтрарности существует
между частными суждениями I и О. I и О
могут быть одновременно истинными, но
не могут быть одновременно ложными
(пример: оба суждения «Некоторые люди
любят логику» и «некоторые люди не
любят логику» — истинны)
Решение
задачи по логическому квадрату
Если
А — истина, то какое значение принимают
Е, I и О.
Решение: по квадрату получается:
если А — истина, то Е-ложь, I-истина,
О-ложь.
Итак,
Если А — истина, то
Е-ложь, I-истина, О-ложь.
Если E истинно,
то А — ложь, I — ложь, О — ложь
Если I
истинно, то Е — ложь, А — неопределенно,
О — неопределенно
Если O истинно, то А
— ложь, Е — неопределенно, I — неопределенно
Если
A ложно, то О — истина, Е — неопределенно,
I — неопределенно
Если E ложно, то I —
истина, А — неопределенно, О —
неопределенно
Если I ложно, то О —
истина, Е — истина, А — ложь
Если O ложно,
то А — истина, Е — ложь, I — истина
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
следует ли заключение с необходимостью? помогите пожалуйста
1. Все студенты нашей группы сдали зачет по логике. Волков зачет по логике не сдал.
2. Боль подтачивает силы человека. Никакая боль нежелательна.
3. Все шутки для того и придуманы, чтобы смешить людей. Ни один парламентский акт не шутка.
4. Ни один француз не любит пудинг. Все англичане любят пудинг.
5. Судебные эксперты обязаны давать правдивые показания. Свидетели обязаны давать правдивые показания.
- заключение
- необходимость
Вопросы:
1.Виды суждений и их логическая характеристика
Суждение — это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком или отношение между предметами.
Любое суждение может быть расценено как истинное (соответствующее действительности) или ложное
Языковой формой суждения является повествовательное предложение (косвенно суждение содержит и риторический вопрос, поскольку он по смыслу является утверждением или отрицанием). Предложения в других грамматических формах (собственно вопросительные, побудительные и т.д.) непосредственно суждениями не являются, поскольку ничего не утверждают и не отрицают.
Простые суждения подразделяются по качеству на: утвердительные и отрицательные,
а по количеству на:
- единичные (что-либо утверждается или отрицается об одном предмете — «Этот свидетель дал показания»);
- общие (что-либо утверждается или отрицается обо всех предметах некоторого класса — «Все свидетели дали показания»);
- частные (что-либо утверждается или отрицается о части предметов некоторого класса — «Некоторые свидетели дали показания»).
По характеру предиката различают суждения:
- атрибутивные. Атрибутивным называется суждение о признаке предмета, например: «Лист зеленый»;
- с отношением. Релятивным называется суждение об отношении между предметами. Например, «Москва больше Красноярска»;
- существования. В суждениях существования выражается сам факт существования или несуществования предмета суждения. Например: «Высшее образование есть».
Скачать в формате doc, теоретические задания по логике, вариант 4
2. Простое атрибутивное суждение (ПАС). Его структура и виды по количеству и качеству.
Полная структура простого суждения включает четыре элемента:
- субъект (S) — понятие, отражающее сам предмет мысли, то, о чем что-то говорится;
- предикат (Р) — понятие, отражающее то, что именно говорится о предмете (его свойство или соотношение с другими объектами);
- связка (в языковой форме выражается словами «есть/не есть», «суть/не суть, «является/не является» и т.п., либо вообще только подразумевается). Отражает наличие /отсутствие определенной связи субъекта и предиката;
- квантор (всеобщности («) — «все», «каждый», «ни один… не» («все … не») и т. п.; существования ($) — «некоторые», «многие», «часть» и т. п.;
Объединяя количественную и качественную характеристики, атрибутивные суждения ()делятся на:
- общеутвердительные (А) — «Все S есть Р»,
- частноутвердительные (I) — «Некоторые S есть Р»,
- общеотрицательные (Е) — «Ни один S не есть Р»,
- частноотрицательные (О) — «Некоторые S не есть Р»
В Средние века были приняты эти буквенные обозначения по первым гласным латинских слов affirmo — утверждаю и nego — отрицаю.
ПРИМЕРЫ:
(А): Все люди (S) дышат воздухом (Р)
(I): Некоторые люди (S) любят ходить в театр (Р)
(Е): Ни один из людей (S) не умеет дышать под водой (Р)
(О): Некоторые люди (S) не умеют ходить на руках (Р)
3. Распределенность терминов в ПАС. Суждения выделяющие и невыделяющие, истинные и ложные
Термин считается распределенным (обозначается»+»), если он взят в полном объеме. Термин считается нераспределенным (обозначается»-«), если он взят в части объема.
ПРИМЕРЫ:
Особое место в классификации суждений по количественной характеристике занимают выделяющие и исключающие суждения.
Выделяющие суждения — те, в которых утверждается, что признак присущ данным предметам объема (всем или некоторым), только им и больше никому на свете (или отсутствует у них и только у них, а всем остальным присущ).
Выделяющие суждения могут быть единичными, частными и общими, например: «Только Иванов написал эту контрольную на отлично» — выделяющее единичное суждение, «Некоторые учащиеся (и только учащиеся) являются школьниками» — выделяющее частноутвердительное суждение, «Все квадраты (и только квадраты) являются прямоугольными ромбами» — выделяющее общеутвердительное суждение (определение).
Невыделяющие суждения — те, в которых утверждается, что признак присущ данным предметам объема, но не только им (или отсутствует у них, но не только у них).
Например: «Все студенты нашей группы, кроме Иванова, сдали зачет по логике». Невыделяющие (исключающие) суждения выражаются предложениями со словами «кроме», «за исключением», «помимо», «не считая» и т.п. Значение выделяющих и исключающих суждений состоит в том, что содержащиеся в них мысли не допускают их неоднозначного понимания. Именно поэтому ряд научных положений, а также законов государства, статей Конституции, уголовно-процессуального и других кодексов выражен в этой логической форме.
Всякое суждение может быть либо истинным, либо ложным, т.е. соответствовать действительности либо не соответствовать ей. Если в суждении утверждается связь, существующая в действительности, или отрицается связь, которая в действительности отсутствует, то такое суждение будет истинным. Например, «Кража — преступление», «Астрология — не наука» — истинные суждения. Если же в суждении утверждается связь, которая в действительности не имеет места, или отрицается существующая связь, то такое суждение является ложным. Например, «Кража не является преступлением», «Астрология — наука» — ложные суждения, они противоречат реальному положению вещей.
Существуют суждения, истинность или ложность которых очевидна или может быть легко установлена (например, «Сегодня солнечный день» или «Федоров — сотрудник милиции»), но нередко они нуждаются в обосновании (например, «Н. совершил должностной подлог» или «К. — соучастник преступления»). Истинность или ложность таких суждений должна быть подтверждена другими суждениями, истинность которых установлена.
4.Соотношения между суждениями по правилам логического квадрата.
Несравнимыми среди простых суждений являются суждения, имеющие различные субъекты или предикаты.
Сравнимыми являются суждения с одинаковыми субъектами и предикатами.
Для иллюстрации отношений между простыми суждениями используется логический квадрат:
Среди сравнимых различают совместимые суждения, которые могут быть одновременно истинными, и несовместимые суждения, которые одновременно истинными быть не могут.
Совместимость бывает трех видов: полная совместимость (эквивалентность); подчинение; частичная совместимость (субконтрарность). Несовместимость бывает двух видов: противоположность (контрарность) и противоречивость (контрадикторность).
I. Отношением подчинения связаны суждения А и I, Е и О. Общие суждения (А и Е) являются подчиняющими, а частные (I, О) подчиненными. Для суждений находящихся в отношении подчинения, имеет значение условие истинности: Если истинно А(Е), то истинно и I(O), но не наоборот.
II. Отношением противоречия связаны суждения Е и I, А и О. Два противоречивых суждения (согласно законам логики) не могут быть одновременно ни истинными, ни ложными Если А — истинно, то О — ложно
Если А — ложно, то О — истинно
Если О — истинно, то А — ложно
Если О — ложно, то А — истинно
Если Е — истинно, то I — ложно
Если Е — ложно, то I — истинно
Если I -истинно, то E — ложно
Если I — ложно, то E — истинно
III. Отношением контрарности (противоположности) связаны только общие суждение А и Е. Закон исключения третьего к таким суждениям не применим. А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными (пример: оба суждения «Все любят логику» и «никто не любит логику» — ложны).
IV. Отношение субконтрарности существует между частными суждениями I и О. I и О могут быть одновременно истинными, но не могут быть одновременно ложными (пример: оба суждения «Некоторые люди любят логику» и «некоторые люди не любят логику» — истинны)
Решение задачи по логическому квадрату
Если А — истина, то какое значение принимают Е, I и О.
Решение: по квадрату получается: если А — истина, то Е-ложь, I-истина, О-ложь.
Итак,
Если А — истина, то Е-ложь, I-истина, О-ложь.
Если E истинно, то А — ложь, I — ложь, О — ложь
Если I истинно, то Е — ложь, А — неопределенно, О — неопределенно
Если O истинно, то А — ложь, Е — неопределенно, I — неопределенно
Если A ложно, то О — истина, Е — неопределенно, I — неопределенно
Если E ложно, то I — истина, А — неопределенно, О — неопределенно
Если I ложно, то О — истина, Е — истина, А — ложь
Если O ложно, то А — истина, Е — ложь, I – истина
5.Логические операции с ПАС: обращение, превращение, противопоставление субъекту и противопоставление предикату.
Обращение
Обращение подчиняется правилу распределенности терминов. Различают простое (чистое) обращение (без ограничения) и обращение с ограничением. Без ограничения обращаются общеотрицательные (Е) и частноутвердительные (1) суждения. С ограничением — общеутвердительные суждения (А). Частноотрицательные суждения (О) не обращаются.
Обращение подчиняется правилу: термин, не распределенный в посылке, не может быть распределен в заключении
Схемы обращения суждений:
(А) Все S суть Р …………………….(I) Некоторые Р суть S
(I) Некоторые S суть Р ……………..(I) Некоторые Р суть S
(Е) Ни одно S не есть Р …………….(Е) Ни одно Р не есть S
ПРИМЕРЫ:
(А) Все студенты нашей группы (S ) сдали экзамены (Р-).
Его обращение:
(I) Некоторые сдавшие экзамены (Р-) — студенты нашей группы (S-)
(I) Некоторые студенты нашей группы (S-) — отличники (Р~).
Его обращение:
(I) Некоторые отличники (Р-) — студенты нашей группы (S-)
(Е) Ни один студент нашей группы (S ) не является неуспевающим (Р)
Обращение:
(Е) Ни один неуспевающий (Р ) не является студентом нашей группы (S )
Превращение
Преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения, называется превращением. Чтобы превратить суждение, нужно изменить его связку на противоположную, а предикат — на противоречащее понятие.
Схемы превращения:
A все S суть P……………………E ни одно S не есть не-P
E ни одно S не суть P……………A все S суть не-P
I некоторые S суть P…………….O некоторые S не суть не-P
O некоторые S не суть P …………I некоторые S суть не-P
ПРИМЕРЫ:
(А) Все сотрудники нашего коллектива — квалифицированные специалисты. Превращение:
(Е) ни один сотрудник нашего коллектива не является неквалифицированным специалистом
(Е) Ни одно религиозное учение не является научным.
Превращение:
(А) всякое религиозное учение является ненаучным
(I)Некоторые государства являются федеративными.
Превращение:
(О) Некоторые государства не являются нефедеративными
(О) Некоторые преступления не являются умышленными.
Превращение:
(I) Некоторые преступления являются неумышленными
Противопоставление субъекту —это преобразование категорического суждения, в результате которого субъектом становится предикат исходного суждения, а предикатом — понятие, противоречащее субъекту исходного суждения.
Такой вывод можно осуществить, последовательно применяя обращение исходного суждения, а затем — превращение полученного результата, либо сразу следуя правилам для противопоставления субъекту:
Схема:
(А) Все S есть Р…………..….Некоторые Р не есть не-S.
(Е)Ни одно S не есть Р……….Все Р есть не-S.
(I)Некоторые S есть Р………..Некоторые Р не есть не-S.
Для частноотрицательных суждений не используются выводы с применением противопоставления субъекту, так как в процессе этого вывода мы должны были бы сделать обращение частноотрицательного суждения, для которого не применяется вывод посредством обращения.
ПРИМЕРЫ:
(Е)Ни один человек, являющийся злым (S),
не есть человек, который может быть вполне справедливым (Р).
Противопоставление субъекту:
Все люди, которые могут быть вполне справедливыми (Р),
есть люди, не являющиеся злыми (не-S).
Противопоставление Предикату— вид непосредственного умозаключения, в котором субъектом вывода является понятие, противоречащее предикату посылки, предикатом является субъект посылки, а связка изменяется на противоположную символически:
Противопоставление предикату представляет собой соединение превращения с обращением, поэтому при его выполнении следует сначала произвести превращение посылки, а затем обратить получившееся суждение: превращаем «S есть Р», получаем «S не есть не-Р», затем обращаем последнее суждение и приходим к выводу «не-Р не есть S». Затруднения здесь носят чисто грамматический характер. Чтобы избежать их, следует формулировать связку в явном виде и фиксировать отрицания. Из общеутвердительного суждения следует общеотрицательный вывод; из общеотрицательного суждения следует частноутвердительный вывод; из частноотрицательного суждения следует частноутвердительный вывод; из частноутвердительного суждения нельзя получить вывод путем противопоставления предикату
Схема противопоставления
A все S суть P………………..ни одно не-P не есть S
E ни одно S не есть P………некоторые не-P суть S
O некоторые S не суть P……некоторые не-P суть S
I некоторые S суть P ………..не используют выводы с применением противопоставления предикату
Термины:
Суждение — это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком или отношение между предметами.
Высказывание — упрощение термина «Суждение» из формальной логики, используется в математической логике. Высказыванием является повествовательное предложение, которое формализует некоторое выражение мысли. Это утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true).
Экзистенциальное суждение — — суждение, которое относится к существованию как таковому. Оно имеет форму: «Л есть» (а именно: налично, сущее, существующее), в отличие от суждения определенного бытия, форма которого: «Л есть Р» (напр., «А есть зеленое»). Логистика различает два вида экзистенциальных высказываний: сингулярное экзистенциальное суждение типа «существует нечто такое, как элементарное количество» и универсальное экзистенциальное суждение типа «существует нечто такое, как цвет».
Суждение отношения — суждение, в котором говорится о том, что определенные отношения имеют место (или не имеют места) между элементами двух, трех и т. д. предметов. Таковыми являются, например, суждения: «Москва больше Рязани», «Каждый следователь знает некоторого адвоката лучше, чем некоторого прокурора». В первом суждении утверждается, что отношение «больший» имеет место между Москвой и Рязанью, во втором утверждается, что отношение «знающий лучше, чем» имеет место между каждым следователем, некоторым адвокатом и некоторым прокурором.
Атрибутивное суждение — суждение, в котором утверждается или отрицается принадлежность свойства предмету. Например: «Роза красная», «Преступник должен быть наказан»
Субъект – это то, о чем что-то утверждается в высказывании
Предикат – это то, что утверждается о субъекте. Например, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».
Связка суждения – является показателем качества суждения
Квантор суждения — это количественная характеристика суждения
Общеутвердительное суждение — общее по объему и утвердительное по качеству связки. Его структура: «Все S есть Р«, а символом служит латинская буква «А«.
Общеотрицательное суждение — общее по объему субъекта и отрицательное по качеству связки. Его структура: «Ни одно S не есть Р«. Символом общеотрицательных суждений служит буква «Е«.
Частноутвердительное суждение — частное по объему субъекта и утвердительное по качеству связки. Его структура: «Некоторые S есть Р«. Символом частноутвердительных суждений служит буква «I«.
Частноотрицательное суждение — частное по объему и отрицательное по качеству связки. Его структура: «Некоторые S не есть Р«, а символом служит буква «О«.
Выделяющие суждения — те, в которых утверждается, что признак присущ данным предметам объема (всем или некоторым), только им и больше никому на свете (или отсутствует у них и только у них, а всем остальным присущ).
Невыделяющие суждения — те суждения, в которых утверждается, что признак присущ данным предметам объема, но не только им (или отсутствует у них, но не только у них).
Распределенность терминов – используется для характеристики соотношения объемов субъекта и предиката. Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него. Термин считается нераспределенным, если его объем лишь частично включается в объем другого термина или частично исключается из него.
Обращение подчиняется правилу распределенности терминов. Различают простое (чистое) обращение (без ограничения) и обращение с ограничением. Без ограничения обращаются общеотрицательные (Е) и частноутвердительные (1) суждения. С ограничением — общеутвердительные суждения (А). Частноотрицательные суждения (О) не обращаются.
Превращение — преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения. Чтобы превратить суждение, нужно изменить его связку на противоположную, а предикат — на противоречащее понятие.
Противопоставление субъекту — это преобразование категорического суждения, в результате которого субъектом становится предикат исходного суждения, а предикатом — понятие, противоречащее субъекту исходного суждения.
Противопоставление предикату — вид непосредственного умозаключения, в котором субъектом вывода является понятие, противоречащее предикату посылки, предикатом является субъект посылки, а связка изменяется на противоположную символически.
Скачать в формате doc, теоретические задания по логике, вариант 4
17,106 просмотров всего, 2 просмотров сегодня