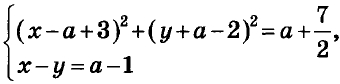Вот она! Загадочная. Нестандартная. Задача 18 Профильного ЕГЭ по математике.
Эта задача оценивается в целых 4 первичных балла, и они пересчитываются в 9-10 тестовых.
Можно ничего не знать. И удачно подобрать пример. И получить 1 балл за пункт (а). Во всяком случае, попробовать это сделать.
А можно потратить 2 часа на перебор вариантов… и так ничего и не найти. Если не знаешь секретов решения этой задачи. ОК, некоторые из секретов мы расскажем.
Действительно, пункт (а) в задаче 18 почти всегда решается сразу. Пункт (б) тоже решается быстро, но только если повезет. Пункт (в) без специальной подготовки решить невозможно.
Необходимая теория для решения задач на числа и их свойства — это всего две страницы. Делимость чисел, наибольший общий делитель и наименьшее общее кратное, основная теорема арифметики, признаки делимости на 3, на 4, на 5, на 8, 9, 10 и 11. Ничего сложного.
Повторите также темы: Арифметическая прогрессия и Геометрическая прогрессия.
Начинать лучше всего с подготовительных задач.
Затем стоит освоить метод «Оценка плюс пример». Для того чтобы применить этот метод, от строгих оценок, которые даны в условии (со знаками > или < ), переходим к нестрогим (со знаками ≥ или ≤ ).
Узнать о секретах решения задания 18 Профильного ЕГЭ по математике.
Узнать больше о решении уравнений в целых числах. В школьных учебниках этого нет.
Один из необходимых навыков для решения пункта (в) – работа с неравенствами. В школьных учебниках этого тоже нет.
Многие считают, что если в этой задаче в пункте (а) ответ «да», то во втором обязательно должно быть «нет». Авторитетно заявляем: нет, необязательно! Может быть любое сочетание из «да» и «нет». И может быть «да» в обоих пунктах, и «нет» в обоих.
Если вопрос в этой задаче (неважно, в каком пункте) формулируется как «Может ли быть…» — и дальше некоторое утверждение, и ваш ответ: «Да», — то одного вашего «Да» недостаточно. Нужен пример. И если вы его подберете, вы не обязаны объяснять, как нашли его.
Если ответ на этот вопрос: «Нет», то вам нужно это доказать. «Нет, потому что…» — и приводите свое доказательство.
В общем, проще показать это на примерах:
1. За прохождение каждого уровня игры на планшете можно получить от одной до трёх звёзд. При этом заряд аккумулятора планшета уменьшается на 3 пункта при получении трёх звёзд, на 6 пунктов при получении двух звёзд и на 9 пунктов при получении одной звезды. Витя прошёл несколько уровней игры подряд.
а) Мог ли заряд аккумулятора уменьшиться ровно на 32 пункта?
б) Сколько уровней игры было пройдено, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
в) За пройденный уровень начисляется 9000 очков при получении трёх звёзд, 5000 — при получении двух звёзд и 2000 — при получении одной звезды. Какое наибольшее количество очков мог получить Витя, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
а) Заметим, что заряд аккумулятора при прохождении уровня уменьшается на 3, 6 или 9 пунктов, и все эти числа делится на 3. Поскольку 32 не делится на 3, заряд не мог уменьшиться на 32 пункта.
б) Да, на 33 пункта заряд мог уменьшиться.
Пусть на х уровнях получено по 3 звезды, на у уровнях — по 2 звезды и на z уровнях — по 1 звезде.
Тогда:
, то есть
.
Сложив уравнения и
, получим, что
(пройдено 7 уровней).
Системе удовлетворяют При этом заряд аккумулятора уменьшился на 33 пункта.
в) Поскольку и
, получаем, что
. Возможны варианты:
, тогда
, получено 47 тысяч очков.
, тогда
, получено 48 тысяч очков.
, тогда
, получено 49 тысяч очков – это максимально возможное количество.
Это была простая задача №18. А вот сложная.
2. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 вырасти в два раза?
б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный балл в школе № 2 равняться 1?
в) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Пусть в первой школе писали тест учеников, а во второй
учеников, причем
,
.
Пусть учащиеся первой школы набрали в сумме балл, а учащиеся второй
баллов.
Тогда средние баллы равны и
.
Пусть из первой школы во вторую перешел ученик, набравший за тест баллов.
а) Предположим, что средний балл в школе № 1 вырос в два раза. Тогда .
Отсюда: .
Поскольку положительно, получаем, что
– противоречие с условием.
Ответ в пункте (а): нет.
б) Во втором пункте ответ тоже «нет». Предположим, что . Получим:
.
Поскольку ,
.
Если ,то
.
Тогда:
. Отсюда:
. Очевидно,
и
.
Что будет, если ? Тогда
.
Подставив эти и
в уравнение
, получим:
,
, противоречие с условием, поскольку
– целое. Значит,
С другой стороны, из условия получаем, что
, значит,
.
Но если , то
и
– получили противоречие.
в) По условию, и в первой, и во второй школах первоначально средний балл был целым числом. Он не может быть равен единице (из пункта (б)). Проверим, может ли он быть равен 2, 3, 4…
Пусть первоначально средний балл равен 2. Тогда
. Условие
по-прежнему должно выполняться.
Преобразуя эти уравнения, получим:
.
Значит, и
. Подходит
и
.
При таких значениях уравнение
имеет решения
или
.
Подставим поочередно пары и
в уравнение
, получим, что целых решений
это уравнение не имеет.
Пусть первоначально средний балл равен 3. Тогда
,
, подходит
, тогда
.
Например, в первой школе тест писали 2 учащихся и набрали 22 и 18 баллов. В школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.
Да, непростая это задача, восемнадцатая задача из варинта ЕГЭ. Но если к ней привыкнуть, потренироваться, то вполне можно решить и заработать необходимые на ЕГЭ баллы. Мы учим решать эту задачу на наших интенсивах в ЕГЭ-Студии, а также на Онлайн-курсе. Многим нашим выпускникам она обеспечила поступление на бюджетные отделения ведущих вузов.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 18. Числа и их свойства u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
За это задание ты можешь получить 4 балла. На решение дается около 40 минут. Уровень сложности: высокий.
Средний процент выполнения: 3.2%
Ответом к заданию 18 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
На доске выписаны числа $7$ и $8$. За один ход надо заменить написанные на доске числа $a$ и $b$ числами $(2a+3)$ и $(2+a+b)$. Например, из чисел $7$ и $8$ можно получить либо числа $(17;17)$, либо числа $(19;17)$.
а) Может ли после нескольких ходов на доске появиться число $77$?
б) Может ли через $101$ ход на доске появиться число $20008$?
в) Может ли через $205$ ходов на доске появиться два одинаковых числа?
Решение
а) Да, может. Пусть после первого хода получили числа (17; 17), после второго хода: 2 · 17 + 3 = 37 и 2 + 17 + 17 = 36; после третьего хода: 2 · 37 + 3 = 77 и 2 + 36 + 37 = 75.
б) Если числа a и b — разной чётности, то число (2a + 3) — нечётное и (2 + a + b) — нечётное.
Если числа a и b — одной чётности, то число (2a + 3) — нечётное, а (2 + a + b) — чётное. Таким образом, после нечётного числа ходов оба выписанных числа — нечётные числа и число 20008 после 101 хода на доске появиться не может.
в) Если после k-го хода на доске выписаны два одинаковых числа — числа n, то после (k + 1)-го хода будет число (2n + 3) и (2 + n + n), то есть (2n + 3) и (2 + 2n); а после (k + 2) хода можно выписать на доске числа 2 · (2n + 3) + 3 = 4n + 9 и 2 + 2n + 3 + 2n + 2 = 4n + 7, либо числа 2(2n + 2) + 3 = 4n + 7 и 2 + 2n + 2 + 2n + 3 = 4n + 7. После первого хода можно получить равные числа (17; 17).
Таким образом, равные числа можно выписать на доске после 1-го, 3-го, 5-го и т.д. ходов, то есть после всех нечётных ходов. Значит, и после 205-го хода могут быть выписаны на доске одинаковые числа.
Ответ: a)да; б)нет; в)да
Задача 2
На доске было написано 20 натуральных чисел (не обязательно различных), каждое из которых не превосходит $24$ и не равно $1$. Среднее арифметическое написанных чисел равнялось $6$. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались не больше $1$, с доски стёрли. а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше $8{,}5$? б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше $9$, но меньше $10$? в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Решение
а) Пусть первоначально на доске было 15 чисел, равных 2, 5 чисел, равных 41. Их среднее арифметическое равно ${15 · 2 + 5 · 18}/{20} = 6$.
Среднее арифметическое получившихся чисел равно ${5 · 9}/{5} = 9 > 8.5$. Среднее арифметическое оставшихся на доске чисел могло быть больше $16.5$.
б) Пусть с доски было стёрто $k$ чисел, сумма оставшихся была равна $S$, а стала ${S}/{2}$. По условию оказались стёрты только числа получившиеся из 2, поэтому ${S + 2k}/{20} = 6$.
Отсюда, $S = 120 — 2k$.
Среднее арифметическое оставшихся чисел равно ${S}/{2(20 — k)}$. Тогда ${120-2k}/{2(20-k)}={60-k}/{20-k}; 9 < {60 — 2k}/{20 — k)} < 10; 180 — 9k < 60 — k < 200 — 10k$,
${table180 — 9k < 60 — k; 60 — k < 200 — 2k;$ ${table8k > 120; 9k < 140;$ ${tablek > 15; k < 15{5}/{9};$. Таких целых чисел $k$ нет.
Среднее арифметическое оставшихся на доске натуральных чисел не могло оказаться больше 9 и меньше 10.
в) Найдём наибольшее возможное значение среднего арифметического $A = {60 — k}/{20 — k}$ оставшихся чисел в зависимости от целочисленного аргумента $k$ — первоначального количества чисел 2 на доске.
Имеем $A = {60 — k}/{20 — k} = 1 + {40}/{20 — k}$.
Число $A$ будет наибольшим, если наибольшим будет значение аргумента $k$. Оценим это значение. Каждое из первоначально написанных на доске чисел было не более $24$, поэтому $120 — 2k ≤ 24(20 — k)$.
$22k ≤ 360, k ≤ 16{4}/{11}, k ∈ N , k ≤ 16$.
Тогда $A ≤ 1 + {40}/{20 — 16} = 11$.
Приведём пример, показывающий, что среднее арифметическое оставшихся на доске чисел действительно могло стать равным $11$. Пусть первоначально на доске было записано 16 чисел, равных 2, 4 числа, равных 22.
Их среднее арифметическое ${16 · 2 + 4 · 22}/{20} =6$.
Среднее арифметическое оставшихся чисел стало равно ${4 · 11}/{4} = 11$.
Ответ: а)да; б)нет; в)11
Задача 3
На доске было написано $30$ натуральных чисел (не обязательно различных), каждое из которых больше $10$, но не превосходит $50$. Среднее арифметическое написанных чисел равнялось $21$. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше $6$, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше $16{,}5$?
б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше $18$, но меньше $19$?
в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Решение
а) Пусть первоначально на доске было 20 чисел, равных 11, 10 чисел, равных 41. Их среднее арифметическое равно ${20 · 11 + 10 · 41}/{30} = 21$.
Среднее арифметическое получившихся чисел равно ${10 · 20.5}/{10} = 20.5$, $20.5 > 16.5$. Среднее арифметическое оставшихся на доске чисел могло быть больше $16.5$.
б) Пусть с доски было стёрто $k$ чисел, сумма оставшихся была равна $S$, а стала ${S}/{2}$. По условию оказались стёрты только числа получившиеся из 11, поэтому ${S + 11k}/{30} = 21$.
Отсюда, $S = 630 — 11k$.
Среднее арифметическое оставшихся чисел равно ${S}/{2(30 — k)}$. Тогда $18 < {630 — 11k}/{2(30 — k)} < 19; 1080 — 36k < 630 — 11k < 1140 — 38k$,
${table1080 — 36k < 630 — 11k; 1140 — 38k > 630 — 11k;$ ${table450 < 25k; 510 > 27k;$ ${tablek > 18; k < 18{24}/{27};$. Таких целых чисел $k$ нет.
Среднее арифметическое оставшихся на доске натуральных чисел не могло оказаться больше 18 и меньше 19.
в) Найдём наибольшее возможное значение среднего арифметического $A = {630 — 11k}/{2(30 — k)}$ оставшихся чисел в зависимости от целочисленного аргумента $k$ — первоначального количества чисел 18 на доске.
Имеем $A = {630 — 11k}/{2(30 — k)} = {11k — 630}/{2k — 60} = {{11}/{2}(2k — 60) — 300}/{2k — 60} = {11}/{2} — {300}/{2k — 60} = {11}/{2} + {150}/{30 — k}$.
Число $A$ будет наибольшим, если наибольшим будет значение аргумента $k$. Оценим это значение. Каждое из первоначально написанных на доске чисел было не более $50$, в конце на доске осталось $30 — k$ чисел, поэтому для суммы оставшихся чисел $S = 630 — 11k$ должно выполняться неравенство $630 — 11k ≤ 50(30 — k)$.
$39k ≤ 870, k ≤ {870}/{39} = 22{12}/{39}, k ∈ N , k ≤ 22$.
Тогда $A ≤ {11}/{2} + {150}/{30 — 22} = 24{1}/{4}$.
Приведём пример, показывающий, что среднее арифметическое оставшихся на доске чисел действительно могло стать равным $24{1}/{4}$. Пусть первоначально на доске было записано 22 числа, равных 11, 7 чисел, равных 50 и 1 число, равное 38.
Их среднее арифметическое ${22 · 11 + 7 · 50 + 38}/{30} = {242 + 350 + 38}/{30} = 21$.
Среднее арифметическое оставшихся чисел стало равно ${7 · {50}/{2} + {38}/{2}}/{8} = {388}/{16} = 24.25$.
Ответ: а)да; б)нет; в)24.25
Задача 4
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно $936$ и а) три; б) четыре; в) пять из них образуют геометрическую прогрессию?
Решение
Разложим число $936$ на простые множители (это может быть сделано единственным образом с точностью до порядка множителей). $936 = 2^3 · 3^2 · 13$.
а) Можно, например, $1, 2, 4, 9, 13$.
б) Предположим, что четыре из пяти различных натуральных чисел, произведение которых равно $936$, составляют возрастающую геометрическую прогрессию. Введём обозначения: $b_1 , b_2 = b_1 · q, b_3 = b_1 · q^2, b_4 = b_1 · q^3$, пятое число обозначим $b_5$.
Тогда $q = {b_2}/{b_1}$, причём $q$ — рациональное число, большее единицы. То гда $q = {m}/{n}$, где $m$ и $n$ — натуральные взаимно простые числа, $m > n ≥ 1$.
Получим:
$936 = b_1 · b_2 · b_3 · b_4 · b_5 = b_1^4 · q^6 · b_5 = b_1^4 · ({m}/{n})^6 · b_5 = b_1^4 · {m^6}/{n^6} · b_5$.
Так как $m$ и $n$ — взаимно просты, то и $m^6$ и $n^6$ взаимно просты. Следовательно, всё произведение $b_1 · b_2 · b_3 · b_4 · b_5$ делится на $m^6$, это означает, что в разложении числа $936$ есть простой множитель в 6-ой степени, получили противоречие. Значит, нельзя.
в) Предположим, что пять различных натуральных чисел, произведение которых равно $936$, составляют геометрическую прогрессию, как и в пункте б) введём обозначения: $b_1, b_2 = b_1 · q, b_3 = b_1 · q^2 , b_4 = b_1 · q^3 , b_5 = b_1 · q^4$. Тогда $q = {b_2}/{b_1}$, причём $q$ — рациональное число, большее единицы.
Тогда $q = {m}/{n}$, где $m$ и $n$ — натуральные взаимно простые числа, $m > n ≥ 1$.
Получим:
$936 = b_1 · b_2 · b_3 · b_4 · b_5 = b_1^5 · q^{10} = b_1^5 · ({m}/{n})^{10} = b_1^5 · {m^{10}}/{n^{10}}$.
Так как $m$ и $n$ — взаимно просты, то и $m^{10}$ и $n^{10}$ взаимно просты. Следовательно, $b_1^5$ делится на $n^{10}$, а всё произведение $b_1 ·b_2 ·b_3 ·b_4 ·b_5$ делится на $m^{10}$, это означает, что в разложении числа $936$ есть простой множитель в 10-ой степени, получили противоречие. Значит, нельзя.
Ответ: а)да; б)нет; в)нет
Задача 5
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 4725 и а) три; б) четыре; в) пять из них образуют геометрическую прогрессию?
Решение
Разложим число $4725$ на простые множители (это может быть сделано единственным образом с точностью до порядка множителей). $4725 = 3^3 · 5^2 · 7$.
а) Можно, например, $1, 3, 9, 25, 7$.
б) Предположим, что четыре из пяти различных натуральных чисел, произведение которых равно $4725$, составляют возрастающую геометрическую прогрессию. Введём обозначения: $b_1 , b_2 = b_1 · q, b_3 = b_1 · q^2, b_4 = b_1 · q^3$, пятое число обозначим $b_5$.
Тогда $q = {b_2}/{b_1}$, причём $q$ — рациональное число, большее единицы. То гда $q = {m}/{n}$, где $m$ и $n$ — натуральные взаимно простые числа, $m > n ≥ 1$.
Получим:
$4725 = b_1 · b_2 · b_3 · b_4 · b_5 = b_1^4 · q^6 · b_5 = b_1^4 · ({m}/{n})^6 · b_5 = b_1^4 · {m^6}/{n^6} · b_5$.
Так как $m$ и $n$ — взаимно просты, то и $m^6$ и $n^6$ взаимно просты. Следовательно, всё произведение $b_1 · b_2 · b_3 · b_4 · b_5$ делится на $m^6$, это означает, что в разложении числа $4725$ есть простой множитель в 6-ой степени, получили противоречие. Значит, нельзя.
в) Предположим, что пять различных натуральных чисел, произведение которых равно $4725$, составляют геометрическую прогрессию, как и в пункте б) введём обозначения: $b_1, b_2 = b_1 · q, b_3 = b_1 · q^2 , b_4 = b_1 · q^3 , b_5 = b_1 · q^4$. Тогда $q = {b_2}/{b_1}$, причём $q$ — рациональное число, большее единицы.
Тогда $q = {m}/{n}$, где $m$ и $n$ — натуральные взаимно простые числа, $m > n ≥ 1$.
Получим:
$4725 = b_1 · b_2 · b_3 · b_4 · b_5 = b_1^5 · q^{10} = b_1^5 · ({m}/{n})^{10} = b_1^5 · {m^{10}}/{n^{10}}$.
Так как $m$ и $n$ — взаимно просты, то и $m^{10}$ и $n^{10}$ взаимно просты. Следовательно, $b_1^5$ делится на $n^{10}$, а всё произведение $b_1 ·b_2 ·b_3 ·b_4 ·b_5$ делится на $m^{10}$, это означает, что в разложении числа $4725$ есть простой множитель в 10-ой степени, получили противоречие. Значит, нельзя.
Ответ: а)да; б)нет; в)нет
Задача 6
На доске написано несколько натуральных чисел, произведение любых двух из которых больше $50$ и меньше $140$. а) Может ли на доске быть $6$ чисел? б) Может ли на доске быть $7$ чисел? в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?
Решение
а) Да. Например, на доске может быть написано шесть чисел 7, 8, 9, 10, 11, 12.
б) Заметим, что среди написанных чисел только одно число может быть больше 11, поскольку произведение любых двух различных натуральных чисел, больших 11, больше 140. Аналогично среди написанных чисел только одно число может быть меньше 8, поскольку произведение любых двух различных натуральных чисел, меньших 8, меньше 50. Таким образом, помимо наименьшего и наибольшего чисел, на доске могут быть написаны только числа 8, 9, 10, 11. Следовательно, на доске не может быть более шести чисел.
в) Пусть на доске написаны числа $a_1 , a_2 , a_3 , a_4$ , причём $a_1 < a_2 < a_3 < a_4$. Тогда для выполнения условий задачи достаточно, чтобы выполнялись неравенства $a_1 · a_2 > 50, a_3 · a_4 < 140$.
В пункте «б» было доказано $8 ≤ a_2 ≤ a_3 ≤ 11$. Рассмотрим возможные случаи.
1. Если $a_2 = 8, a_3 = 9$, то $8a_1 > 50, 9a_4 < 140$, получаем $a_1 = 7, 10 ≤ a_4 ≤ 15$. В этом случае наибольшее возможное значение суммы достигается при $a_1 = 7, a_4 = 15, 7 + 8 + 9 + 15 = 39$.
2. Если $a_2 = 9, a_3 = 10$, то $9a_1 > 50, 10a_4 < 140$, получаем $6 ≤ a_1 ≤ 8, 11 ≤ a_4 ≤ 13$. В этом случае, наибольшее возможное значение суммы достигается при $a_1 = 8, a_4 = 13, 8 + 9 + 10 + 13 = 40$.
3. Если $a_2 = 10, a_3 = 11$, то $10a_1 > 50, 11a_4 < 140$, получаем $6 ≤ a_1 ≤ 9, a_4 ≤ 12$. В этом случае наибольшее возможное значение суммы достигается при $a_1 = 9$ и $a_4 = 12, 9 + 10 + 11 + 12 = 42$.
4. Если $a_2 = 8, a_3 = 10$, то $8a_1 > 50, 10a_4 < 140$, получаем $a_1 = 7, 11 ≤ a_4 ≤ 13$. В этом случае, наибольшее возможное значение суммы достигается при $a_1 = 7, a_4 = 13, 7 + 8 + 10 + 13 = 38$.
5. Если $a_2 = 8, a_3 = 11$, то $8a_1 > 50 a_4 = 12$, получаем $a_1 = 7, a_4 = 12$. В этом случае наибольшее возможное значение суммы $7+8+11+12 = 38$.
6. Если $a_2 = 9, a_3 = 11$, то $9a_1 > 50, a_4 = 12$, получаем $6 ≤ a_1 ≤ 8, a_4 = 12$.
В этом случае наибольшее возможное значение суммы достигается при $a_1 = 8, a_4 = 12, 8 + 9 + 11 + 12 = 40$.
Таким образом, наибольшее значение суммы равно $42$.
Ответ: а)да, б)нет, в)42
Задача 7
На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше $30$ и меньше $80$. а) Может ли на доске быть $4$ числа? б) Может ли на доске быть $5$ чисел? в) Какое наибольшее значение может принимать сумма чисел на доске, если их три?
Решение
а) Да, например, на доске может быть написано 6, 7, 8, 9.
б) Заметим, что среди написанных чисел только одно число может быть больше 8, поскольку произведение любых двух различных натуральных чисел, больших 8, больше 80. Аналогично, среди написанных чисел только одно число может быть меньше 7, поскольку произведение любых двух различных натуральных чисел, меньших 7, не больше 30. Таким образом, помимо наибольшего и наименьшего чисел, на доске могут быть написаны только числа 7 или 8. Следовательно, на доске не может быть более четырёх чисел.
в) Пусть на доске написаны числа $a_1 , a_2 , a_3$, причём $a_1 < a_2 < a_3$. Тогда для выполнения условий задачи достаточно, чтобы выполнялись неравенства $a_1 · a_2 > 30, a_2 · a_3 < 80$.
В пункте «б» было доказано, что $a_2 = 7$ или $a_2 = 8$.
Разберём возможные случаи. Если $a_2 = 7$, то $7a_1 > 30, 7a_3 < 80$, откуда $a_1 = 5$ или $a_1 = 6, 8 ≤ a_3 ≤ 11$. В этом случае наибольшее значение достигается при $a_1 = 6, a_3 = 11$, равно $6 + 7 + 11 = 24$.
Если $a_2 = 8$, то $8a_1 > 30, 8a_3 < 80$, откуда $4 ≤ a_1 ≤ 7, a_3 = 9$.
В этом случае наибольшее значение при $a_1 = 7$ равно $7 + 8 + 9 = 24$.
Таким образом наибольшее значение суммы равно $24$.
Ответ: а)да, б)нет, в)24
Задача 8
Множество чисел назовём особенным, если его можно разбить на два подмножества с одинаковой суммой чисел. а) Является ли множество ${750; 751; … , 949}$ особенным? б) Является ли множество ${9^2; 9^3; … . 9^{2018}}$ особенным? в) Сколько особенных четырёхэлементных подмножеств у множества ${2; 3; 6; 7; 15; 19; 25; 28}$?
Решение
а) Разобьём множество {750; 751; . . . ; 949} на 100 пар, сумма чисел в каждой из которых равна 1699: (750; 949), (751; 948), . . .
Множество {750; 751; . . . ; 949} можно разбить на два подмножества, в каждом из которых 50 таких пар. Значит, суммы чисел в этих двух подмножествах одинаковы и множество {750; 751; . . . ; 949} является особенным.
б) Заметим, что $9^{2018} > {9^{2018}− 81}/{8} = 9^2 + 9^3 + . . . + 9^{2017}$. Поэтому сумма чисел в подмножестве, содержащем $9^{2018}$, всегда больше суммы остальных чисел, следовательно, множество {$9^2; 9^3; . . . 9^{2018}$} не является особенным.
в) Заметим, что четырёхэлементное множество является особенным в двух случаях: либо одно число является суммой трёх других, либо множество содержит две пары с равными суммами. В первом случае возможны только следующие подмножества {2; 7; 19; 28}; {3; 6; 19; 28}; {6; 7; 15; 28}; {3; 7; 15; 25}; {2; 6; 7; 15}
Заметим, что сумма всех чисел особенного подмножества чётна. В исходном множестве три чётных числа, поэтому в особенное подмножество входят либо два из них, либо ни одного. Если входят числа 2 и 6, то либо сумма двух других чисел равна 8, либо их разность равна 4. Получаем особенные подмножества {2; 3; 6; 7}; {2; 6; 15; 19}. Если входят числа 2 и 28, то либо сумма двух других чисел равна 30, либо их разность равна 26. Таких подмножеств нет. Если входят числа 6 и 28, то либо сумма двух других чисел равна 34, либо их разность равна 22. Получаем особенные подмножества {3; 6; 25; 28}; {6; 15; 19; 28}. Если в особенном подмножестве нет чётных чисел, то особенное подмножество лежит во множестве {3; 7; 15; 19; 25}. Получаем следующее особенное подмножество (две пары с равными суммами): {3; 7; 15; 19}. Всего 10 особенных подмножеств.
Ответ: а)да; б)нет; в)10
Задача 9
Коля берёт пять различных натуральных чисел и проделывает с ними следующие операции: сначала находит среднее геометрическое первых двух чисел, затем — среднее геометрическое третьего числа и полученного результата, после — среднее геометрическое четвёртого числа и полученного результата, а затем — среднее геометрическое пятого числа и полученного результата. Полученный результат он обозначает через $K$. Затем Коля считает среднее геометрическое исходных чисел — число $P$. а) Возможно ли, что $K=P^5$? б) Возможно ли, что $K=P$? в) Для какого наибольшего целого числа $m$ возможно, что $K>P^m$?
Решение
а) Пусть Коля задумал различные натуральные числа $a, b, c d, e$. Тогда $K =√{e√{d√{c√{ab}}}} = a^{{1}/{16}}b^{{1}/{16}}c^{{1}/{8}}d^{{1}/{4}}e^{{1}/{2}}, P = √^5{abcde} = (abcde)^{{1}/{5}}$. Если $K = P^5$, то $a^{{1}/{16}}b^{{1}/{16}}c^{{1}/{8}}d^{{1}/{4}}e^{{1}/{2}} = abcde$, иными словами, $abc^2d^4e^8 = a^{16}b^{16}c^{16}d^{16}e^{16}$, отсюда $a^{15}b^{15}c^{14}d^{12}e^8 = 1$, что невозможно, так как числа $a, b, c d$ и $e$ — различные натуральные и среди них хотя бы 4 больше 1, а тогда $a^{15}b^{15}c^{14}d^{12}e^8 > 1$ и равенство $K = P^5$ невозможно.
б) Предположим, что $K = P$, тогда $a^{{1}/{16}}b^{{1}/{16}}c^{{1}/{8}}d^{{1}/{4}}e^{{1}/{2}} = (abcde)^{{1}/{5}}$, отсюда $a^5b^5c^{10}d^{20}e^{40} = (abcde)^{16}; d^4e^{24} = a^{11}b^{11}c^6$. Покажем, что это равенство может быть выполнено. Подберём пример, считая числа $a, b, c, d$ и $e$ различными степенями одного и того же числа, например 2. Пусть $a = 2^2, b = 2^4, c = 2^3, d = 2^{15}, e = 2$, требуемое достигается.
в) Пусть $K > P^m$, тогда $a^{{1}/{16}}b^{{1}/{16}}c^{{1}/{8}}d^{{1}/{4}}e^{{1}/{2}} > (abcde)^{{m}/{5}}; a^5b^5c^{10}d^{20}e^{40} > (abcde)^{16m}$ тогда $a^{(16m-5)}b^{(16m-5)}c^{(16m-10)}d^{(16m-20)}e^{(16m-40)} < 1$.
Это неравенство невозможно при $m ≥ 3$, так как при $m ≥ 3$ степени чисел $a, b, c, d$ и $e$ больше 1, а тогда и их произведение больше 1.
Приведём пример для $m = 2$. Тогда должно выполняться $a^{27}b^{27}c^{22}d^{12} < e^8$. Пусть $a = 2; b = 2^2, c = 2^3, d = 2^4, e = 2^{30}$, неравенство выполняется.
Ответ:
Задача 10
Маша задумала $6$ различных натуральных чисел и проделывает с ними такую операцию: сначала находит среднее арифметическое первых двух чисел, затем — среднее арифметическое полученного результата и третьего числа, после — среднее арифметическое полученного результата и четвёртого числа, затем — среднее арифметическое полученного числа и пятого числа, и наконец — среднее арифметическое полученного результата и шестого числа. Полученный результат она обозначает через $M$. Далее Маша находит число $A$ — среднее арифметическое исходных чисел.
а) Возможно ли, что $A=M$?
б) Возможно ли, что $M=6A$?
в) Найдите наибольшее натуральное значение $n$, для которого возможно, что $M=nA$.
Решение
а) Пусть Маша задумала числа $a, b, c, d, e$ и $f$. Тогда $M = {a + b + 2c + 4d + 8e + 16f}/{32}; A = {a + b + c + d + e + f}/{6}$.
$M = A$, тогда и только тогда, когда $3a + 3b + 6c + 12d + 24e + 48f = 16a + 16b + 16c + 16d + 16e + 16f; 8e + 32f = 13(a + b) + 10c + 4d$.
Пусть $a = 1, b = 3, c = 6, d = 4, e = 8, f = 2$. При этих значениях требуемое равенство выполнено.
б) Предположим, что $M = 6A$. Тогда ${a + b + 2c + 4d + 8e + 16f}/{32} = a + b + c + d + e + f, 31a + 31b + 30c + 28d + 24e + 16f = 0$.
Это равенство невозможно, так как $a, b, c, d, e$ и $f$ — натуральные числа.
в) Пусть $M = nA$, тогда $3a + 3b + 6c + 12d + 24e + 48f = 16n(a + b + c + d + e + f)$,
$(16n — 3)a + (16n — 3)b + (16n — 6)c + (16n — 12)d + (16n — 24)e +(16n — 48)f = 0$.
При $n ≥ 3$ это равенство невозможно, так как $a, b, c, d, e$ и $f$ — натуральные числа.
Приведём пример для $n = 2$. Тогда должно выполняться равенство $29(a + b) + 26c + 20d + 8e = 16f$.
Пусть $a = 1, b = 3, c = 2, d = 4, e = 5, f = 18$. При этих значениях равенство выполняется.
Ответ: а)да; б)нет; в)2
Задача 11
На окружности в случайном порядке были расположены натуральные числа от $1$ до $13$. Над каждой парой соседних чисел написали модуль их разности, после чего исходные числа стёрли.
а) Могла ли сумма оставшихся чисел равняться $30$?
б) Могла ли сумма оставшихся чисел равняться $14$?
в) Найдите наибольшее возможное значение суммы оставшихся чисел.
Решение
а) Да, могла. Пусть числа записаны в следующем порядке (считая по часовой стрелке): $1; 2; 5; 3; 4; 6; 7; 8; 13; 12; 11; 9; 10$. Сумма модулей рассматриваемых разностей равна 30.
б) Нет, не могла. Предположим противное. Модуль каждой разности — натуральное число, причём всего выписано 13 модулей разности. Их сумма равна 14, если одна из этих разностей равна 2, а 12 других равна 1. Это означает, что соседними с числом 1 могут быть только числа 2 и 3, при этом |3 — 1| = 2, то есть оставшиеся модули разностей должны равняться 1. Но тогда числа 2 и 3 не могут быть соседними. Значит вторым соседним числом с числом 2 будет число a ≥ 4. Но тогда |a-2| ≥ 2.Изначит, сумма всех модулей разности не меньше, чем |3-1|+|a-2|+11 ≥ 15. Получили противоречие. Следовательно, требуемое не возможно.
в) Пусть изначально на доске были выписаны числа в следующем порядке по часовой стрелке: $a_1, a_2, . . . , a_13$, где каждое $a_k$ — одно из натуральных чисел от 1 до 13. Заметим, что $|a_1 — a_2| + |a_2 — a_3| + |a_3 — a_4| + … + |a_12 — a_13| + |a_13 — a_1| = (x_1+x_2+x_3+…+x_13)-(y_1+y_2+y_3+… y_13)$. Каждый модуль $|a_i-a_{i+1}|$ (i = 1, 2, . . . 13) представлен в виде $x_i -y_i$, где $x_i$ — большее из чисел $a_i$ и $a_{i+1}$, $y_i$ — меньшее из них. Аналогично, $|a_{13} -a_1| = x_{13} -y_{13}$. Каждое $a_k$ встречается среди чисел $x_1, x_2, . . . , x_{13}, y_1, y_2, . . . , y_{13}$ ровно 2 раза. Тогда $x_1+x_2+x_3+…+x_{13} ≤ 2·13+2·12+2·11+2·10+2·9+2·8+7 = 133$, а $y_1+y_2+y_3+…+y_{13} ≥ 2·1+2·2+2·3+2·4+2·5+2·6+7 = 49$. Отсюда $(x_1 + x_2 + x_3 + … + x_{13}) — (y_1 + y_2 + y_3 + … + y_{13}) ≤ 133 — 49 = 84$, то есть сумма записанных модулей разностей не превышает 84. Приведём пример, в котором указанная сумма равна 84. Пусть на доске изначально числа в следующем порядке (по часовой стрелке): $1; 13; 2; 12; 3; 11; 4; 10; 5; 9; 6; 8; 7.$
Тогда $|1-13|+|13-2|+|2-12|+|12-3|+|3-11|+|11-4|+|4-10|+ +|10 — 5| + |5 — 9| + |9 — 6| + |6 — 8| + |8 — 7| + |7 — 1| = 84$.
Ответ: а)да; б)нет; в)84
Задача 12
На окружности в случайном порядке были расположены натуральные числа от $1$ до $16$. Над каждой парой соседних чисел написали модуль их разности, после чего исходные числа стёрли и посчитали сумму $s$ оставшихся модулей разностей. а) Могло ли оказаться, что $s=40$? б) Могло ли оказаться, что $s=41$? в) Найдите максимально возможное значение $s$.
Решение
а) Да, могло. Приведём пример. Пусть по часовой стрелке числа записаны в следующем порядке: $1$; $2$; $3$; $4$; $5$; $6$; $7$; $8$; $9$; $10$; $16$; $11$; $15$; $13$; $14$; $12$. Сумма модулей указанных разностей равна $40$. б) Нет, не могло. Пусть изначально на доске в порядке следования по часовой стрелке записаны числа $a_1$, $a_2$, $a_3$, … , $a_{16}$ — переставленные натуральные числа от $1$ до $16$. Заметим, что для произвольных натуральных чисел $m$ и $n$ числа $m-n$ и $n-m$ имеют одинаковую чётность, а значит $|m-n|$ имеет ту же чётность, что $m-n$. Но тогда сумма $|a_1-a_2|+|a_2-a_3|+|a_3-a_4|+ … +|a_{15}-a_{16}|+|a_{16}-a_1|$ будет
нечётной только в том случае, если сумма
$(a_1-a_2)+(a_2-a_3)+(a_3-a_4)+ … +(a_{15}-a_{16})+(a_{16}-a_1)$ будет нечётной, но последняя сумма равна $0$, следовательно, чётна. Отсюда сумма $|a_1-a_2|+|a_2-a_3|+|a_3-a_4|+ … +|a_{15}-a_{16}|+|a_{16}-a_1|$ чётна и не может равняться $41$. в) Заметим, что $|a_1-a_2|+|a_2-a_3|+|a_3-a_4|+ … +|a_{15}-a_{16}|+|a_{16}-a_1|=$
$=(x_1+x_2+x_3+… +x_{16})-(y_1+y_2+y_3+… y_{16})$. Каждый модуль $|a_i-a_{i+1}|$ ($i=1, 2, … 15$) представлен в виде, $x_i-y_i$, где $x_1$ — большее из чисел $a_i$ и $a_{i+1}$, $y_i$ — меньшее из них. Аналогично $|a_{16}-a_1|=x_{16}-y_{16}$. Причём каждое $a_k$ встречается среди чисел $x_1$, $x_2$, …, $x_{16}$, $y_1$, $y_2$, …, $y_{16}$ ровно $2$ раза. Тогда $x_1+x_2+x_3+… +x_{16}⩽ 16+16+15+15+… +9+9=200$, а $y_1+y_2+y_3+… +y_{16}⩾ 1+1+2+2+… +8+8=72$. Отсюда $(x_1+x_2+x_3+… +x_{16})-(y_1+y_2+y_3+… +y_{16})⩽200-72=128$, то есть сумма записанных модулей разностей не превышает $128$. Приведём пример, в котором указанная сумма равна $128$. Пусть на доске изначально числа в следующем порядке (по часовой стрелке): $1$; $16$; $2$; $15$; $3$; $14$; $4$; $13$; $5$; $12$; $6$; $11$; $7$; $10$; $8$; $9$. Тогда $|1-16|+|16-2|+|2-15|+|15-3|+|3-14|+|14-4|+|4-13|+$
$+|13-5|+|5-12|+|12-6|+|6-11|+|11-7|+|7-10|+|10-8|+|8-9|+$
$+|9-1|=128$.
Ответ: а)да; б)нет; в)128
Задача 13
Два мастера на протяжении некоторого числа дней изготавливали одинаковые детали. Сергей Петрович в первый день изготовил $s$ деталей, а Пётр Сергеевич — $p$ деталей, $s$ и $p$ — натуральные числа. Каждый последующий день каждый из мастеров изготавливал на $10$ деталей больше, чем в предыдущий. Всего за эти дни Сергей Петрович изготовил на $2261$ деталь больше, чем Пётр Сергеевич. а) Могло ли это быть за $20$ дней? б) Могло ли это быть за $19$ дней, если Сергей Петрович за все дни изготовил не более $3000$ деталей? в) Какое наибольшее количество деталей мог изготовить Сергей Петрович, если Пётр Сергеевич в последний день изготовил менее $300$ деталей?
Решение
а) Каждый день Сергей Петрович изготавливает на (s — p) деталей больше, чем Пётр Сергеевич. Тогда за 20 дней Сергей Петрович изготовил на 20(s — p) деталей больше. Должно выполняться равенство 20(s-p) = 2261, но 2261 нацело не делится на 20. Следовательно, требуемое невозможно.
б) Если Сергей Петрович изготовил не более 3000 деталей, то Пётр Сергеевич не более 739 деталей. За 19 дней Сергей Петрович изготовил бы не менее, чем ${2 + 192}/{2}·19 = 1843$ деталей. Значит, требуемое не возможно.
в) Пусть рабочие делали детали в течение n дней, тогда $n(s — p) = 2261 = 7·17·19$. При этом в последний день Пётр Сергеевич изготовил p + 10(n — 1) деталей, p + 10(n — 1) < 300, 10(n — 1) < 300, n ≤ 60. Значит, n натуральный делитель числа 2261, не превосходящий 60. Таким образом n = 1, n = 7, n = 17 или n = 19. Пусть Пётр Сергеевич за все дни изготовил R деталей, тогда Сергей Петрович (R + 2261). Следовательно, наибольшее возможное количество деталей, изготовленных Сергеем Петровичем, будет при наибольшем количестве деталей, изготовленных Петром Сергеевичем. $R = {2p + 10(n — 1)}/{2}·n$ При каждом фиксированном значении n значение R тем больше, чем больше p, то есть R — наибольшее при p = 309 — 10n и $R = {608 — 10n}/{2}·n = 304n — 5n^2 = (304 — 5n)·n$. При n = 1 R = 299. При n = 7 R = 1883. При n = 17 R = 3723. При n = 19 R = 3971.
Наибольшее число деталей, изготовленных Сергеем Петровичем, равно 3971 + 2261 = 6232.
Ответ: а)нет; б)нет; в)6232
Задача 14
Две девочки делают фотографии во время туристической поездки. В первый день Катя сделала $k$ фотографий, а Маша — $m$ ($k⩾1$, $m⩾1$). Каждый последующий день каждая из девочек делает на $1$ фотографию больше, чем в предыдущий. Всего за время поездки Маша сделала на $715$ фотографий больше, чем Катя. а) Могло ли это произойти за $5$ дней? б) Могла ли Катя за $11$ дней сделать $1000$ фотографий? в) Определите максимальное количество фотографий, которое могла сделать Маша за все эти дни, если Катя в последний день поездки сделала меньше $35$ фотографий.
Решение
а) Да, возможно. Маша с первого по 5 день сделала бы в сумме m + (m + 1) + (m + 2) + (m + 3) + (m + 4) фотографии, а Катя k + (k + 1) + (k + 2) + (k + 3) + (k + 4) фотографий. Тогда (m+4)+(m+3)+(m+2)+(m+1)+m-(k+4)-(k+3)-(k+2)-(k+1)-k = = 5(m — k). Значит, должно выполняться равенство 5(m — k) = 715, m- k = 143. Пусть Катя в первый день сделала одну фотографию, а Маша 144. Тогда за 5 дней Маша сделает на 715 фотографий больше.
б) Нет, не может. Предположим, что это возможно. Тогда m+ (m+1)+ …+ (m+ 10) = 1000; 11m = 1000-55, но (1000- 55) не делится нацело на 11, значит получили противоречие.
в) Пусть девочки делали фотографии в течение n дней. Тогда Маша сделала на m + (m+ 1) + (m+ 2) + … (m + n — 1) — k — (k + 1) — … …-(k+n-1) = n(m-k) фотографий больше. Значит, n(m-k) = 715, n делитель числа 715. Но 715 = 5·11·13, все его натуральные делители это числа 1, 5, 11, 13, 55, 65, 143, 715. В последний день Катя сделала k + (n — 1) фотографий, k + (n — 1) < 35, но k ≥ 1, следовательно (n — 1) < 34, n < 35. Тогда n = 1, n = 5, n = 11 или 13. Так как за все дни Маша сделала на 715 фотографий больше, чем Катя, то большее количество фотографий, сделанных Машей, будет при наибольшем количестве фотографий, сделанных Катей. За n дней Катя сделала s = k + (k + 1) + … + (k + (n — 1)) = ${2k + n — 1}/{2}·n$ фотографий. При каждом фиксированном n это количество тем больше, чем больше k, но k + (n — 1) < 35, то есть k + n < 36, k < 36 — n. При n = 1 наибольшее k = 34 и s = ${2·34}/{2}$ = 34. При n = 5 наибольшее k = 30 и s = ${2·30 + 4}/{2}·5$ = 160. При n = 11 наибольшее k = 24 и s = ${2·24 + 10}/{2}·11$ = 319. При n = 13 наибольшее k = 22 и s = ${2·22 + 12}/{2}·13$ = 364. Тогда наибольшее количество Машиных фотографий равно 364 + 715 = 1079.
Ответ: а)да; б)нет; в)1079
Задача 15
Для $20$ студентов профессор подготовил две контрольные работы. Любой студент может написать только одну из них или обе. За каждую контрольную работу можно получить от $0$ до $30$ баллов. Средний балл за каждую из контрольных работ равен $24$. Каждый студент называет наивысший из полученных им баллов профессору. Если студент написал одну работу, то он называет балл за неё. а) Может ли среднее арифметическое всех поданных баллов быть меньше $24$? б) Может ли среднее арифметическое равняться $21$, если обе конт-
рольные написали только $2$ студента? в) Какое наименьшее количество студентов должно было написать обе контрольные, чтобы среднее арифметическое названных баллов равнялось $21$?
Решение
а) Пусть два человека написали обе контрольные, за каждую из них набрав по 30 баллов. И пусть 9 человек написали только первую контрольную (двое на — 18 баллов и семеро на — 24 балла). Аналогично, пусть только вторую контрольную написали 9 оставшихся студентов (двое на — 18 баллов и семеро на — 24 балла). Тогда средний балл за каждую контрольную равен ${30·2 + 18·2 + 7·24}/{11} = 24$. Среднее арифметическое названных баллов равно ${30·2 + 18·4 + 24·14}/{20} = 23.4 < 24$.
б) Нет, не может. Предположим противное. Тогда сумма названных баллов равна $21·20 = 420$. Всего написанных контрольных 22 и сумма набранных за них баллов равна $22·24 = 528$. При этом, 528 — 420 = 108, то есть 108 баллов из заработанных не были поданы профессору. Эти 108 баллов могли быть заработаны только двумя студентами, которые написали обе контрольные. Каждый из них не назвал баллы за 1 контрольную, то есть не более 30 баллов. В сумме количество баллов, не поданных профессору, не превышает $2·30 = 60$. Но $108 > 60$, поэтому наше предположение не верно.
в) Пусть k студентов написали обе контрольные, тогда всего было написано (20 + k) работ и общее количество заработанных баллов равно 24(20 + k) = 480 + 24k. Сумма баллов, названных профессору, равна $21·20 = 420$. Тогда не поданными остались (480+ 24k — 420) = 60 + 24k баллов. Эти баллы могли быть получены только теми студентами, которые написали обе контрольные. Каждый из этих студентов оставил не поданными не более 30 баллов (30 — максимальный балл за одну контрольную). Следовательно, всего осталось не поданными не более 30k баллов. Получим неравенство $60 + 24k ≤ 30k$, отсюда $k ≥ 10$.
Приведём пример для k = 10. Пусть 10 студентов написали обе контрольные на 30 баллов, 5 — только первую контрольную (каждый на 12 баллов), 5 — только вторую контрольную (каждый на 12 баллов). Тогда среднее арифметическое названных баллов равно ${30·10 + 12·10}/{20} = 21$.
Средний балл за каждую контрольную равен ${30·10 + 5·12}/{15} = 24$.
Ответ: а)да; б)нет; в)10
Задача 16
Для $52$ студентов профессор подготовил две контрольные работы. Любой студент может написать только одну из них или обе. За каждую контрольную работу можно получить от $0$ до $30$ баллов. Средний балл за каждую из контрольных работ равен $17$. Каждый студент называет наивысший из полученных им баллов профессору. Если студент написал одну работу, то он называет балл за неё.
а) Может ли среднее арифметическое всех названных баллов быть больше $17$?
б) Может ли среднее арифметическое равняться $13$, если обе контрольные написали ровно четыре студента?
в) Какое наименьшее количество студентов должно было написать обе контрольные, чтобы среднее арифметическое названных баллов могло равняться $13$?
Решение
а) Пусть два студента написали обе контрольные на $4$ балла, $25$ студентов написали только первую контрольную (двое — на $30$ баллов, $23$ — на $17$ баллов), $25$ студентов написали только вторую контрольную (двое — на $30$ баллов, $23$ — на $17$ баллов). Тогда средний балл за каждую контрольную равен ${2⋅ 4+2⋅ 30+23⋅17} / {27}=17$, а средний балл среди названных равен ${2⋅ 4+4⋅ 30+46⋅17} / {52}=17{,}5>17$.
б) Нет, не может. Предположим противное. Тогда сумма названных баллов равна $13⋅ 52=676$. Всего написанных контрольных $56$ и сумма набранных за них баллов равна $56⋅ 17=952$. При этом $952-676=276$, то есть $276$ баллов из числа заработанных не было подано профессору. Эти $276$ баллов могли быть заработаны только теми $4$ студентами, которые написали обе контрольные. Каждый из них не назвал балл за $1$ контрольную, то есть не более $30$ баллов. В сумме количество баллов, не поданных профессору, не превышает $4⋅ 30=120$. Но $120<276$, поэтому наше предположение не верно.
в) Пусть $n$ студентов написали обе контрольные, тогда всего было написано $(52+n)$ работ и общее количество заработанных баллов равно $17(52+n)=884+17n$. Сумма баллов, поданных профессору, равна $52⋅ 13=676$. Тогда не поданными остались $(884+17n)-676$ баллов, то есть $208+17n$ баллов. Эти баллы могли быть получены только теми студентами, которые написали обе контрольные. Каждый из этих студентов оставил не поданными не более $30$ баллов. Следовательно, всего остались не поданными не более $30n$ баллов. Получим неравенство $208+17n⩽30n$, $n⩾16$. Приведём пример для $n=16$. Пусть $16$ студентов написали обе контрольные на $30$ баллов, $18$ — только первую контрольную ($3$ — на $30$ баллов, $1$ — на $8$, остальные на $0$) и $18$ написали только вторую контрольную с теми же результатами.
Ответ: а)да; б)нет; в)16
Задача 17
На доске написаны $40$ натуральных чисел. Какие-то из них белые, а какие-то — зелёные. Белые числа кратны $9$, зелёные кратны $4$. Все белые числа отличаются друг от друга, все зелёные тоже отличаются друг от друга, среди чисел разных цветов могут быть одинаковые. а) Может ли сумма всех написанных чисел быть меньше $3280$, если все они зелёные? б) Может ли сумма всех чисел равняться $2453$, если только $1$ число белое? в) Найдите наименьшее количество белых чисел, если сумма всех чисел равна $2453$.
Решение
а) Нет, не может. Наименьшая сумма $40$ различных натуральных чисел, кратных $4$, равна $4·1+ 4·2+ . . .+ 4·40=4(1 + 2 + … + 40) = {4·41·40}/{2}= 3280$.
б) Нет, не может. Сумма $17$ чисел, оканчивающихся на $7$, не меньше, чем $7 + 17 + … + 167 = {7 + 167}/{2}·17 = 1479$. Значит, при $17$ числах с последней цифрой $7$ сумма всех выписанных чисел больше $840$.
б) Нет, не может. Если только $1$ число белое, то остальные $39$ чисел — зелёные и их сумма не меньше чем $4·1 + 4·2 + … + 4·39 = 4(1 + 2 + … 39) = 4·{40·39}/{2} = 3120$, а сумма всех чисел не меньше, чем $3120 + 9 = 3129$.
в) Пусть $m$ — количество белых чисел, тогда зелёных чисел выписано $(40 — m)$. Сумма всех выписанных чисел не меньше, чем $9(1+2+…+m)+4(1+2+…+40-m) = 9·{(m+ 1)m}/{2} +4·{(41 -m)(40 -m)}/{2}$. Должно выполняться неравенство ${9(m+ 1)m}/{2} + {4(41-m)(40 -m)}/{2} ≤ 2453, 13m^2 — 315m + 1654 ≤ 0$. Перебирая натуральные значения $m$, получаем, что наименьшее значение $m$, для которого выполнено это неравенство, равно $8$. Действительно, при $m ≤ 5, 315m < 1654$, следовательно, $13m^2 — 315m + 1654 > 0$. При $m = 6, 13m^2 > 360, 13m^2 + 1654 > 2000, 315m < 2000$. Аналогично, при $m = 7$ выполняется $13m^2-315m+1654 > 0$. При $m = 8$ выполняется $13m^2-315m+1654 < 0$. Построим пример для $m = 8$. Наименьшее значение суммы в этом случае равно $9·{9·8}/{2} +4·{33·32}/{2} = 2436$, что на $17$ меньше требуемой суммы.
Учитывая, что $17 = 9 + 4 + 4$, построим один из возможных примеров. Выписаны белые числа $9·1, 9·2, . . . , 9·6, 9·7$ и $9·9$ и зелёные числа $4·1, 4·2, . . . , 4·30, 4·31$ и $4·34$.
Ответ: а)нет; б)нет; в)8
Задача 18
На доске написано $30$ различных натуральных чисел, каждое из которых или оканчивается на $7$, или чётное. Сумма всех чисел равна $840$. а) Может ли на доске быть выписано ровно $28$ чётных чисел? б) Может ли быть на доске ровно $17$ чисел, оканчивающихся на $7$? в) Найдите наибольшее возможное количество чисел, оканчивающихся на $7$, среди выписанных.
Решение
а) Да, может. Пусть выписаны $2$ числа, оканчивающиеся на $7: 7, 17$ и $28$ чётных чисел: $2, 2·2, 2·3, 2·4, . . . 2·26, 2·27$, а так же число $60$.
б) Нет, не может. Сумма $17$ чисел, оканчивающихся на $7$, не меньше, чем $7 + 17 + … + 167 = {7 + 167}/{2}·17 = 1479$. Значит, при $17$ числах с последней цифрой $7$ сумма всех выписанных чисел больше $840$.
в) Пусть на доске $n$ чисел, оканчивающихся на $7$. Тогда остальные $(30 — n)$ чисел чётны. Значит, сумма всех выписанных чисел не меньше чем $7 + 17 + … (7 + (n — 1)·10) + 2·1 + 2·2 + … + 2(30 — n) = {14 + (n — 1)10}/{2}·n + {(30 — n)(31 — n)}/{2}·2 = 6n^2 — 59n + 930$.
Должно выполняться неравенство $6n^2 — 59n + 930 ≤ 840$, то есть $6n^2 — 59n + 90 ≤ 0$. Решим уравнение $6n^2 — 59n + 90 = 0$, получим $n_{1,2} = {59±√{1321}}/{12}$. Неравенство $6n^2 — 59n + 90 ≤ 0$ выполнено при ${59 — √{1321}}/{12} ≤ n ≤ {59 + √{1321}}/{12}$.
Тогда $n ≤ {59 + √{1321}}/{12} ≤ {59 + 37}/{12} = 8$. Так как $n$ натуральное число, то $n ≤ 7$. Количество чисел, оканчивающихся на $7$, должно быть чётным, иначе сумма всех выписанных чисел была бы нечетна. Приведём пример для $n = 6$. Пусть выписаны числа $7, 17, 27, 37, 47, 57$, а так же $21, . . . 2·23$ и число $96$.
Ответ: а)да; б)нет; в)6
Задача 19
На доске написано $30$ различных натуральных чисел, каждое из которых или оканчивается на $1$, или чётное. Сумма всех чисел равна $771$. а) Может ли на доске быть выписано ровно $4$ числа, оканчивающихся на $1$? б) Может ли быть выписано ровно $13$ чисел, оканчивающихся на $1$? в) Найдите наименьшее возможное количество чисел, оканчивающихся на $1$, среди выписанных.
Решение
а) Нет, не может. Сумма $4$ чисел, оканчивающихся на $1$, чётна, сумма $26$ чётных чисел — тоже чётна, следовательно, сумма $4$ чисел, оканчивающихся на $1$, и $26$ чётных чисел — чётна и не равна $771$. б) Нет. Если на доске выписаны $13$ разных чисел, оканчивающихся на $1$, то их сумма не меньше чем $1+11+… +111+121={122} / {2}⋅ 13=793>771$. Тогда сумма всех выписанных чисел тем более больше $771$. в) Пусть на доске $n$ чисел, оканчивающихся на $1$, тогда $(30-n)$ чисел — чётные. Следовательно, сумма всех чисел не меньше чем $1+11+…+(1+10(n-1))+2⋅ 1+2⋅ 2+… +2⋅ (30-n)=$ ${1+1+10(n-1)} / {2}⋅ n+{(30-n)(31-n)} / {2}⋅2=6n^2-65n+930$. Должно выполняться неравенство $6n^2-65n+930⩽771$, то есть $6n^2-65n+159⩽0$. Решим уравнение $6n^2-65n+159=0$, $ n_{1,2}={65±√ {409}} / {12}$. Неравенство $6n^2-65n+159⩽0$ выполняется при ${65-√ {409}} / {12}⩽ n⩽{65+√ {409}} / {12}$. Значит, $n⩾{65-√ {409}} / {12}>{65-21} / {12}>3$. Так как $n$ — натуральное число, то $n⩾4$. Но $n$ должно быть нечётным (иначе сумма всех чисел была бы чётной), значит, $n⩾5$. Приведём пример для $n=5$. Пусть выписаны числа $1$, $11$, $21$, $31$, $41$, а также $2⋅1$, $2⋅2$, $2⋅ 3$, … $2⋅ 24$ и число $66$.
Ответ: а)нет; б)нет; в)5
Задача 20
На доске выписаны числа $10$ и $11$. За один ход надо заменить написанные на доске числа $a$ и $b$ числами ($2a+1$) и ($a+b$). Например, из чисел $10$ и $11$ можно получить либо $21$ и $21$, либо числа $21$ и $23$. а) Может ли после нескольких ходов на доске появиться число $95$? б) Может ли после $1003$ ходов на доске появиться число $20018$? в) Укажите наибольшую разность чисел через $2018$ ходов.
Решение
а) Да, может. Пусть после первого хода получены числа 21 и 23, после второго 44 и 47, после третьего 91 и 95.
б) Если числа a и b разной чётности, то числа (2a + 1) и (a + b) нечётные, если числа a и b — одной чётности, то (2a + 1) — нечётно, а (a + b) — чётное. Таким образом, после нечётного числа ходов на доске выписаны два нечётных числа и число 20018 выписано быть не может.
в) Если выписаны числа a и b и a $≤$ b, то их разность b-a и следующим ходом будут выписаны числа 2b + 1 и a + b, их разность (b — a + 1) или числа 2a + 1 и a + b, их неотрицательная разность |b — a — 1|.
Таким образом, разность каждый раз изменяется на 1 и будет наибольшей, если каждый ход будет увеличивается на 1. Тогда её значение 1 + 2018 = 2019.
Ответ: а)да; б)нет; в)2019
Рекомендуемые курсы подготовки
Решение и ответы заданий Варианта №18 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
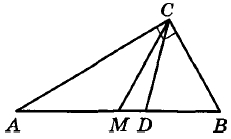
Угол между биссектрисой CD и медианой СМ проведёнными из вершины прямого угла С треугольника АВС, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задание 2.
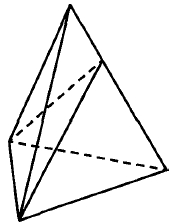
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Задание 3.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России.
Задание 4.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Задание 5.
Найдите корень уравнения log4 25x+7 = 3.
Задание 6.
Найдите значение выражения frac{a^{3,33}}{ a^{2,11}cdot a^{2,22}} при а = frac{2}{7}.
Задание 7.
Прямая у = 9х + 6 является касательной к графику функции у = ах2 – 19х + 13. Найдите а.
Задание 8.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 километра. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Задание 9.
Первый садовый насос перекачивает 10 литров воды за 5 минут, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литра воды?
Задание 10.
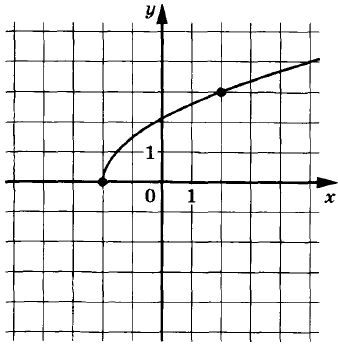
На рисунке изображён график функции f(x) = ksqrt{x+p}. Найдите f(0,25).
Задание 11.
Найдите наибольшее значение функции у = 2х2 – 12х + 8lnх – 5 на отрезке [frac{12}{13};frac{14}{13}].
Задание 12.
а) Решите уравнение 7cosx – 4cos3x = 2√3sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; –3π].
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.
Задание 14.
Решите неравенство log52(x4) – 28log0,04 (x2) ≤ 8.
Задание 15.
Производство х тыс. единиц продукции обходится в q = 3х2 + 6х + 13 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<3.
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{5}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{8}]+[frac{n}{23}]=n+2021?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 3367 | Оценки экспертов решений задания 18 ЕГЭ по математике профильного уровня. Задание 18 проверяет достижение следующих целей изучения математики на профильном уровне: «развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и её приложений в будущей профессиональной деятельности |
Критерии оценивания решений задания 18 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку | |
| 3366 | Имеются три коробки: в первой коробке — 64 камня, во второй — 77 камней, а в третьей — пусто. За один ход разрешается взять по камню из двух коробок и положить в оставшуюся. Сделали некоторое количество таких ходов. а) Может ли в первой коробке оказаться 64 камня, во второй — 59, в третьей — 18? б) Может ли в третьей коробке оказаться 141 камень? в) В первой коробке оказался один камень. Найдите наибольшее возможное количество камней в третьей коробке. |
Имеются три коробки: в первой коробке — 64 камня, во второй — 77 камней, а в третьей — пусто ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 18 Санкт-Петербург, Центр | |
| 3363 | На доске написано N различных натуральных чисел, каждое из которых не превосходит 99. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b − a, и ни одно из написанных чисел не является делителем числа b − a. а) Могли ли на доске быть написаны какие-то два числа из чисел 18, 19 и 20? б) Среди написанных на доске чисел есть 17. Может ли N быть равным 25? в) Найдите наибольшее значение N |
На доске написано N различных натуральных чисел, каждое из которых не превосходит 99 ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 18 Санкт-Петербург, Центр | |
| 3287 | Юра записывает на доске n-значное натуральное число, не используя цифру 0. Затем он записывает рядом ещё одно число, полученное из исходного перемещением первой цифры на последнее место. (Например, если n=3 и исходное число равно 123, то второе число равно 231.) После этого Юра находит сумму этих двух чисел. а) Может ли сумма чисел на доске равняться 2728, если n=4 ? б) Может ли сумма чисел на доске равняться 83 347, если n=5? в) При n=6 оказалось, что сумма чисел делится на 99. Сколько натуральных чисел от 925 111 до 925 999, которые Юра мог использовать в качестве исходного числа? |
Юра записывает на доске n-значное натуральное число, не используя цифру 0 ! Тренировочная работа №1 по МАТЕМАТИКЕ 10-11 класс 27.01.2022 Вариант МА2100109 Задание 18 | |
| 3043 | А) Можно ли в выражении ln5*ln6*ln7*ln8*ln10*ln12*ln14 вместо всех знаков * так расставить знаки «+» и «-«, чтобы в результате получился ноль? Б) Можно ли в выражении ln6*ln7*ln8*ln12*ln14*ln24*ln32 вместо всех знаков * так расставить знаки «+» и «-«, чтобы в результате получился ноль? В) Какое наибольшее количество попарно различных чисел можно выбрать из набора ln7, ln8, …, ln20 и расставить знаки «+» и «-» так, чтобы их сумма стала равна нулю? |
А) Можно ли в выражении ln5*ln6*ln7*ln8*ln10*ln12*ln14 вместо всех знаков * так расставить знаки ! Тренировочный вариант 365 от Ларина Задание 18 (19) # Решение — Кирилла Колокольцева # математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 12 Задание 18 | |
| 2874 | Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1). а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 9 нулями? б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 23 нулями? в) Сколько существует натуральных чисел n, меньших 100, для каждого из которых десятичная запись числа n∙ (100 — n)! оканчивается ровно 23 нулями |
Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1) ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 19 | |
| 2690 | Пусть S(n) и K(n) обозначают сумму всех цифр и сумму квадратов всех цифр натурального числа соответственно. а) Существует ли такое натуральное число n, что K(n) = 2S(n) + 7 ? б) Существует ли такое натуральное число n, что K(n) = 3S(n) + 7 ? в) Для какого наименьшего натурального числа n выполнено равенство K(n) = 8S(n) + 65? |
Пусть S(n) и K(n) обозначают сумму всех цифр и сумму квадратов всех цифр натурального числа ! Статград — Тренировочная работа №1 для 10 класса 28.01.2021 Профильный уровень Вариант МА2000309 Задание 19 | |
| 2680 | Пусть bar(ab) обозначает двузначное число, равное 10a + b , где a и b — цифры, a ≠ 0 . а) Существуют ли такие попарно различные ненулевые цифры a , b, c и d , что bar(ab) ⋅ bar(cd) − bar(ba) ⋅ bar(dc) =198? б) Существуют ли такие попарно различные ненулевые цифры a , b , c и d , что bar(ab) ⋅ bar(cd) − bar(ba) ⋅ bar(dc) =495 , если среди цифр a , b, c и d есть цифра 5? в) Какое наибольшее значение может принимать выражение bar(ab) ⋅ bar(cd) − bar(ba) ⋅ bar(dc) , если среди цифр a , b, c и d есть цифры 5 и 6 |
Пусть ab обозначает двузначное число, равное 10a + b , где a и b — цифры, ! Тренировочная работа №2 по математике 11 класс Статград 16-12-2020 профильный уровень Вариант МА2010209 Задание 19 | |
| 2551 | У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 10 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 15 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая. a) Может ли у Миши быть 30 монет? б) Какое наибольшее количество монет может быть у Миши? в) Какая наибольшая сумма рублей может быть у Миши? |
У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 19 | |
| 2455 | На доске написано 35 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись оканчивается на цифру 7. Сумма всех записанных на доске чисел равна 1135. а) Может ли на доске быть ровно 31 четное число? б) Могут ли ровно семь чисел на доске оканчиваться на 7? в) Какое наибольшее количество чисел, оканчивающихся на 7, может быть на доске? |
На доске написано 35 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись оканчивается на цифру 7 ! Тренировочный вариант 322 от Ларина Задание 19 # Решение — Кирилла Колокольцева | |
- ЕГЭ по математике профиль
Разбор Задачи №18 из Реaльного ЕГЭ 2021 по математике (Основная волна).
Задание 18 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Задача 18 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ по математике заветные 4 первичных балла за задачу 18 (с параметром), данное видео будет полезным для вас.
Связанные страницы:
ЕГЭ №18 (19). Теория чисел. Рекуррентная задача – самая сложная задача мартовского статграда 2021
ЕГЭ 18 (19) – это задачи на теорию чисел, на свойства чисел, на последовательности. Что такое рекуррентная последовательность?
Сейчас узнаете…
Последовательности чисел нам хорошо известны ещё с 8 – 9 класса. Например, прогрессии – арифметическая и геометрическая.
На ЕГЭ довольно часто попадаются задачи на последовательности – как на стандартные прогрессии, так и на необычные – у каждой из которых какая-то своя формула. И формулы у таких последовательностей обычно рекуррентные – то есть такие, когда каждое следующее число вычисляется через значения каких-то предыдущих.
Например, самая известная не-прогрессия – это последовательность Фибоначчи: каждое число равно сумме двух предыдущих.
Такие последовательности – это не просто очередные бессмысленные упражнения математиков (которым, как известно, делать нечего, вот и грузят всех своими задачками). Последовательности очень часто встречаются нам в жизни, и с их помощью очень удобно описывать некоторые процессы.
Например, говорят, что Фибоначчи свою последовательность придумал, наблюдая за размножением кроликов: первые 2 месяца жизни кролик просто растёт, а потом начинает каждый месяц рожать нового кролика (в среднем).
Сколько будет кроликов через полгода? Через год? В задаче 18 (19 из последнего статграда нам попалась как раз такая последовательность.
Смотрите видео, и вы научитесь исследовать такие последовательности, а также узнаете, как правильно решается эта задача.