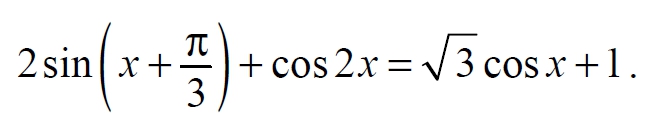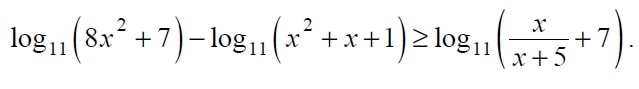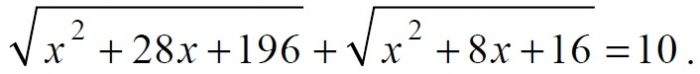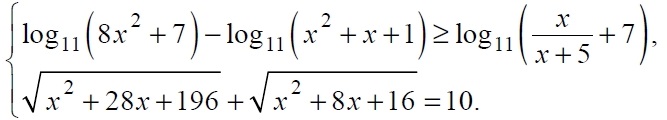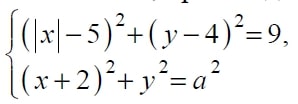Разбор первой части егэ по математике профильный уровень 2022 - Помощь в подготовке к экзаменам и поступлению

Задание 1

1.1	Найдите корень уравнения 3^{x-5}=81.	Смотреть видеоразбор
1.2	Найдите корень уравнения sqrt{3x+49}=10.	Смотреть видеоразбор
1.3	Найдите корень уравнения log_8(5x+47)=3.	Смотреть видеоразбор
1.4	Решите уравнение sqrt{2x+3}=x.	Смотреть видеоразбор

Задание 2

2.1	В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.	Смотреть видеоразбор
2.2	Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?	Смотреть видеоразбор

Задание 3

3.1	Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.	Смотреть видеоразбор
3.2	Площадь треугольника ABC равна 24; DE – средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.	Смотреть видеоразбор
3.3	В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.	Смотреть видеоразбор
3.4	Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.	Смотреть видеоразбор

Задание 4

Задание 5

Задание 6

Задание 7

7.1

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

v=c cdot frac{f-f_0}{f+f_0}

где c = 1500 м/с – скорость звука в воде, f₀ – частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Смотреть видеоразбор

Задание 8

8.1	Весной катер идёт против течения реки в 1 frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).	Смотреть видеоразбор
8.2	Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?	Смотреть видеоразбор
8.3	Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?	Смотреть видеоразбор

Задание 9

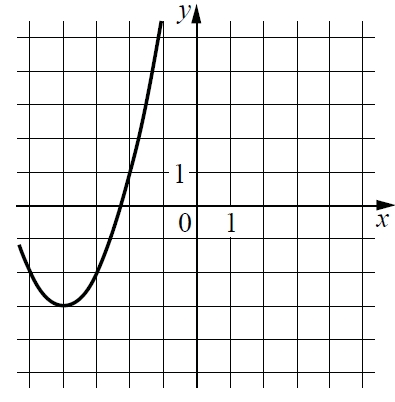
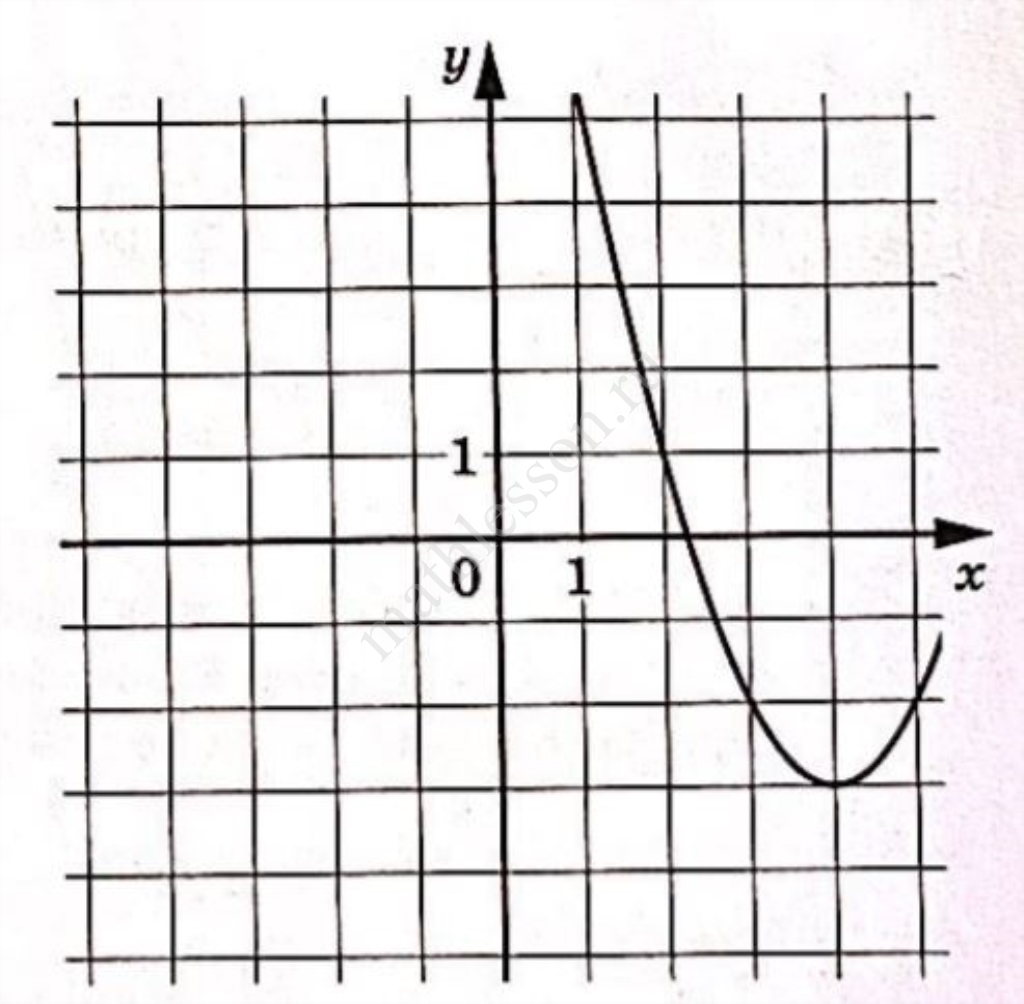
9.1

На рисунке изображён график функции вида f(x) = ax^2+bx+c=0, где числа a, b, c — целые. Найдите значение f(-12).

Смотреть видеоразбор

Задание 10

10.1	Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?	Смотреть видеоразбор
10.2	В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».	Смотреть видеоразбор

Задание 11

Источник

Задание 1

Задание 2

2.1	В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.	Смотреть видеоразбор
2.2	Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?	Смотреть видеоразбор

Задание 3

3.1	Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.	Смотреть видеоразбор
3.2	Площадь треугольника ABC равна 24; DE – средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.	Смотреть видеоразбор
3.3	В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.	Смотреть видеоразбор
3.4	Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.	Смотреть видеоразбор

Задание 4

Задание 5

Задание 6

Задание 7

7.1

v=c cdot frac{f-f_0}{f+f_0}

Смотреть видеоразбор

Задание 8

8.1	Весной катер идёт против течения реки в 1 frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).	Смотреть видеоразбор
8.2	Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?	Смотреть видеоразбор
8.3	Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?	Смотреть видеоразбор

Задание 9

9.1

На рисунке изображён график функции вида f(x) = ax^2+bx+c=0, где числа a, b, c — целые. Найдите значение f(-12).

Смотреть видеоразбор

Задание 10

10.1	Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?	Смотреть видеоразбор
10.2	В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».	Смотреть видеоразбор

Задание 11

Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

Задание 1.
Найдите корень уравнения log₂(7 – x) = 5.

Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.

ИЛИ

В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Задание 3.
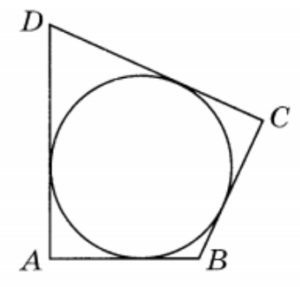
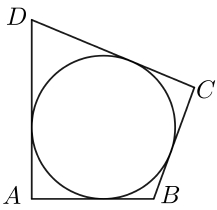
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.

ИЛИ

В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.

Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}

ИЛИ

Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}

Задание 5.
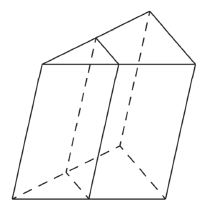
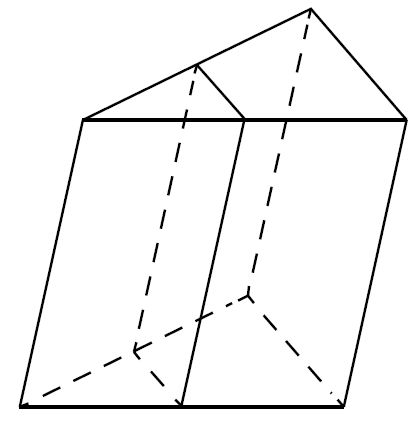
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

ИЛИ

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.

Задание 6.
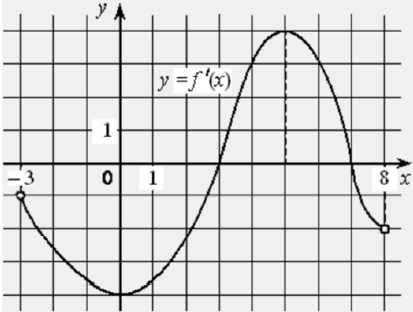
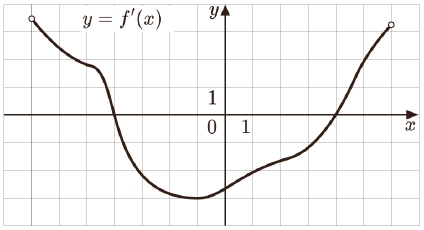
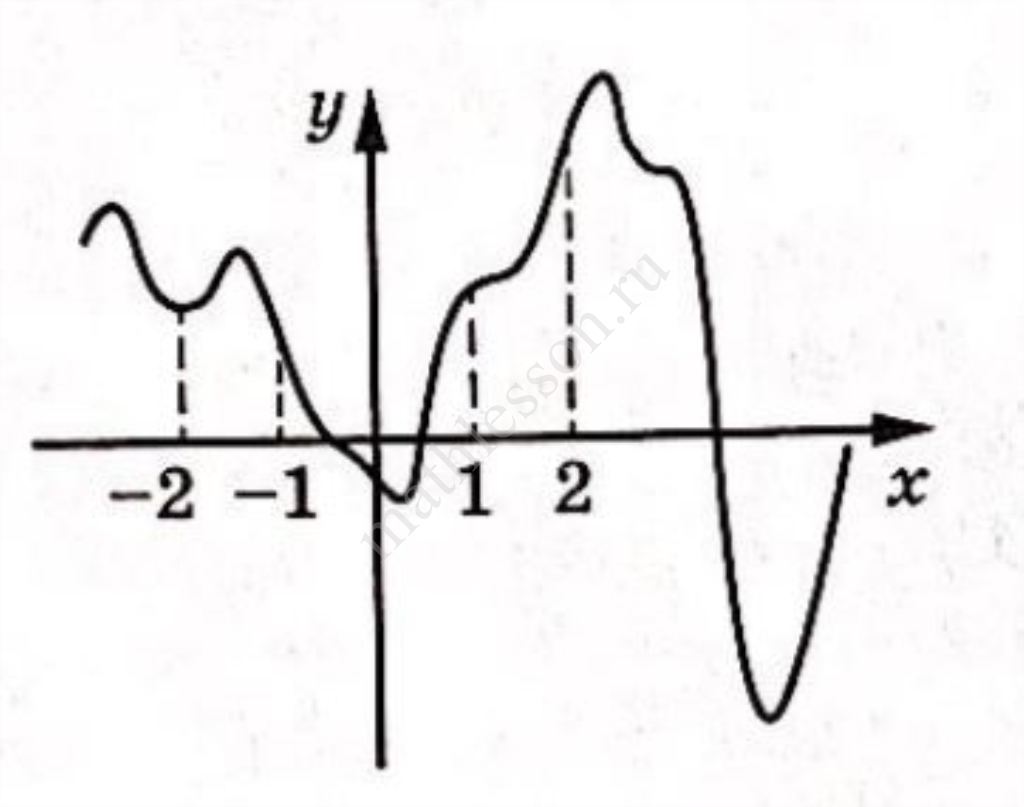
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).

ИЛИ

На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).

Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: , где f₀ = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.

ИЛИ

В розетку электросети подключены приборы, общее сопротивление которых составляет R₁ = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R₂ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R₁ Ом и R₂ Ом их общее сопротивление дается формулой R_общ = (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.

Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

ИЛИ

Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Задание 9.
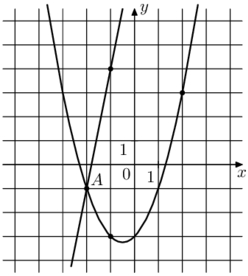
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax² + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

ИЛИ

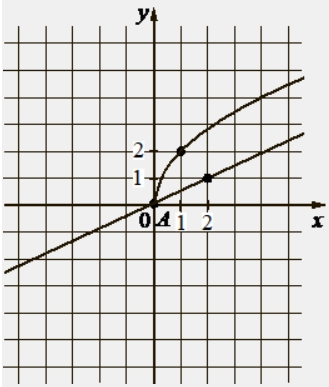
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.

Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

ИЛИ

Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.

Задание 12.
а) Решите уравнение 4^{sin x} + 4^{sin(x + π)} = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].

Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.

Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1

Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?

Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.

Задание 17.
Найдите всe значения параметра a, при каждом их которых система

begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, y=ax. end{cases}

имеет ровно 3 различных решения.

Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?

Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.7 / 5. Количество оценок: 12

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Источник

4 июня 2022

В закладки

Обсудить

Жалоба

Полный вариант профильного уровня по математике от 2 июня с подробным разбором.

02_06_2022.pdf

00:00 — Введение
00:53 — Задание №1
01:49 — Задание №2
03:00 — Задание №3
05:29 — Задание №4
08:41 — Задание №5
11:11 — Задание №6
17:12 — Задание №7
22:27 — Задание №8
31:12 — Задание №9
39:00 — Задание №10
45:16 — Задание №11
51:10 — Задание №12
1:15:20 — Задание №13
1:34:35 — Задание №14 (1 тип задания)
1:43:40 — Задание №15
1:56:56 — Задание №16 (1 тип задания)
2:10:25 — Задание №16 (2 тип задания)
2:31:12 — Задание №16 (3 тип задания)
2:41:03 — Задание №16 (4 тип задания)
2:50:13 — Задание №16 (5 тип задания)
3:02:31 — Задание №17 (1 способ решения)
3:27:40 — Задание №17 (2 способ решения)
3:43:26 — Задание №14 (2 тип задания)
3:55:38 — Задание №18 (1 способ решения, 1 тип задания)
4:09:30 — Задание №18 (2 способ решения, 1 тип задания)
4:12:17 — Задание №18 (2 тип задания)

Источник: youtube.com/c/Профиматика

Источник

Решение ПРОЕКТа (перспективная модель) ЕГЭ 2022 по математике (профильный уровень). Демоверсия ФИПИ для 11 класса. Комплексные числа.

Задание 1.
Найдите корень уравнения 3^x–5 = 81

ИЛИ

Найдите корень уравнения

ИЛИ

Найдите корень уравнения log₈ (5x + 47) = 3

ИЛИ

Решите уравнение . Если корней окажется несколько, то в ответ запишите наименьший из них.

Задание 2.

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

ИЛИ

Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?

Задание 3.

На рисунке изображён график функции вида f(x) = ax² + bx + c, где числа a, b и c – целые. Найдите значение f(−12).

Задание 4.

Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.

ИЛИ

Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.

ИЛИ

В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.

ИЛИ

Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.

Задание 5.
Найдите sin2α, ecли cosα = 0,6 и π < a < 2π.

ИЛИ

Найдите значение выражения 16·log₇⁴√7

ИЛИ

Найдите значение выражения 4^1/5·16^9/10

Задание 6.

В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.

ИЛИ

Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

ИЛИ

Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?

Задание 7.
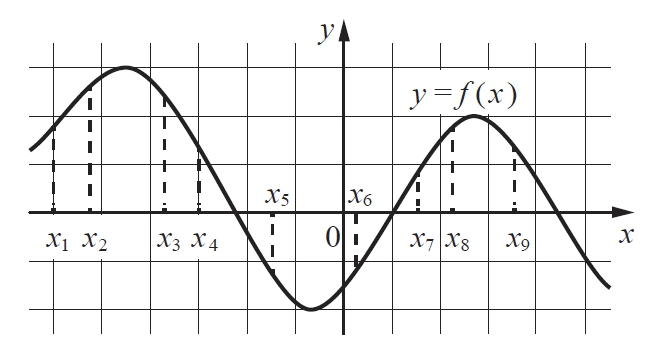
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, … x₉.

Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.

ИЛИ

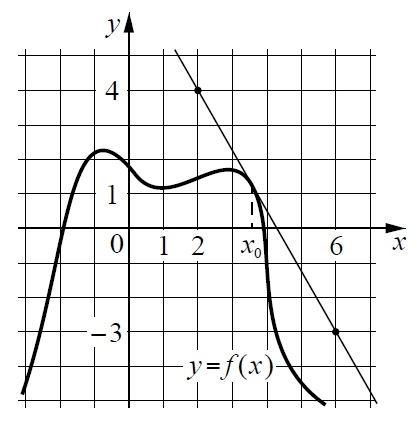
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(x) в точке х₀.

ИЛИ

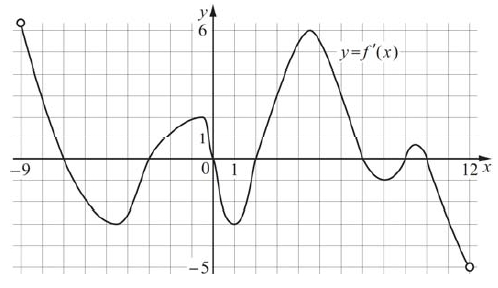
На рисунке изображён график y = f ‘(x) – производной функции f (x), определённой на интервале (−9;12) . В какой точке отрезка [−8;11] функция f (x) принимает f (x) наибольшее значение?

Задание 8.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

где с = 1500 м/с — скорость звука в воде, f₀– частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Задание 9.
Весной катер идёт против течения реки в 1 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

ИЛИ

Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?

ИЛИ

Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?

Задание 10.
Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?

ИЛИ

В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».

Задание 11.
Про комплексное число z известно, что |z − 4 − 7i| = |z + 4 − i|. Найдите наименьшее значение |z|.

Задание 12.
Найдите наименьшее значение функции

y = 9x – 9ln(x + 11) + 7

на отрезке [–10,5 ; 0].

ИЛИ

Найдите точку максимума функции y = (x + ² ∙ e^3–x

ИЛИ

Найдите точку минимума функции

Задание 13.
Решите уравнение

Задание 15.
а) Решите неравенство

ИЛИ

б) Решите уравнение

ИЛИ

в) Решите систему

Задание 16.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.

Задание 18.

Найдите все положительные значения a, при каждом из которых система

имеет единственное решение.

Источник варианта: fipi.ru

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 4

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Задание 1

Найдите корень уравнения $$4^{5x+2}=0,8cdot 5^{5x+2}$$

Ответ: -0,2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Ответ: 0,25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3

В тупоугольном треугольнике АВС известно, что АС=ВС=10, высота АН равна $$sqrt{51}$$. Найдите косинус угла АСВ.

Ответ: -0,7

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4

Найдите значение выражения $$frac{5sin 61^{circ}}{sin 299^{circ}}$$

Ответ: -5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Ответ: 72

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6

На рисунке изображён график y=f(x). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Ответ: -1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7

При температуре 0°C рельс имеет длину l₀=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t_{0})=l_{0}(1+alpha cdot t^{circ})$$, где $$alpha=1,2cdot 10^{-5}$$(°C) — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.

Ответ: 50

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.

Ответ: 17,5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9

На рисунке изображён график функции $$f(x)=ax^{2}+bx+c$$, где числа a,b и с — целые. Найдите $$f(-5)$$.

Ответ: 72

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10

Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 30% этих стёкол, вторая — 70%. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 4 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ: 0,043

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11

Найдите наименьшее значение функции $$y=frac{4}{3}xsqrt{x}-3x+9$$ на отрезке $$[0,25;30]$$.

Ответ: 6,75

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12

а) Решите уравнение $$2sin^{3}(pi+x)=frac{1}{2}cos (x-frac{3pi}{2})$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi}{2};-frac{5pi}{2}]$$

Ответ: а) $$pi k;pm frac{pi}{6}+pi n, k,n in Z$$ б) $$-frac{19pi}{6};-3pi;-frac{17pi}{6}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13

В правильной треугольной пирамиде SABC сторона основания АВ равна 16, высота SH равна 10. Точка К — середина бокового ребра SA. Плоскость, параллельная плоскости АВС, проходит через точку К и пересекает рёбра SB и SC в точках Q и Р соответственно.

а) Докажите, что площадь четырёхугольника BCPQ составляет $$frac{3}{4}$$ треугольника SBC.

б) Найдите объём пирамиды KBCPQ.

Ответ: $$80sqrt{3}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14

Решите неравенство: $$(4^{x}-5cdot 2^{x})-20(4^{x}-5cdot 2^{x})leq 96$$

Ответ: $$(-infty;0];[2;3]$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15

В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы:

— в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20 % по сравнению с концом предыдущего года;

— в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;

— к июлю 2033 года кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?

Ответ: 600 тыс. руб.

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16

Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём АЕ=ED=CD, а прямые АС и BE перпендикулярны. Отрезки АС и BD пересекаются в точке Т.

а) Докажите, что прямая ЕС пересекает отрезок TD в его середине.

б) Найдите площадь треугольника АВТ, если BD=6, $$AE=sqrt{6}$$

Ответ: $$frac{8sqrt{}5}{3}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 17

Найдите все значения а, при каждом из которых уравнение $$|x^{2}-a^{2}|=|x+a|cdot sqrt{x^{2}-4ax+5a}$$ имеет ровно один корень.

Ответ: $$-5;(0;1)$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18

На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.

а) Может ли сумма этих чисел быть равна 2022?

б) Может ли сумма этих чисел быть равна 2021?

в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?

Ответ: а)да б)нет в)97

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Источник

24 августа вышла демоверсия ЕГЭ 2023 по профильной математике. Для тех, кто пока не готов вникать в тему основательно, успокоительный спойлер: почти ничего не изменилось, принципиально новых заданий нет. Всё в порядке.

А для тех, кто давно был на низком старте и ждал разбор демо ЕГЭ, математик Эйджей провёл стрим с решением заданий из демоверсии ЕГЭ 2023 по профильной математике. В этой статье собраны резюме по заданиям экзамена, которые составители ЕГЭ представили в демоверсии.

https://youtu.be/RFQwP8DW8sA

Что изменилось в ЕГЭ 2023 по профильной математике

По сути, никаких критически важных изменений в демоверсии ЕГЭ 2023 нет, о чём составители написали прямо: «Изменения в содержании КИМ отсутствуют». Но есть момент: все задания из первой части, кроме 11, изменили свои номера.

Будем искать позитивные моменты: если в 2022 году вы не смогли запомнить номера заданий в тесте — ничего страшного, запомните новые в 2023 году.

Главное, что новых заданий не появилось.

Важный момент в самостоятельной подготовке к ЕГЭ по профильной математике — выбор качественных сборников задач. Делимся лучшими ресурсами для повторения теории и отработки практики.

1, 2 задания

В демоверсии ЕГЭ 2023 по профильной математике всё начинается с простой геометрии и стереометрии. Составители хотят, чтобы геометрические задачи научились решать как можно больше ребят, поэтому поместили эти задания вперёд как одни из самых простых, чтобы поднять решаемость.

3, 4 задания

Задания 3–4 посвящены теории вероятности.

Задание 3 — обычная задача наподобие задачи из ОГЭ, а задание 4 — задача про монеты и проценты из КИМа 2022 года.

5, 6 задания

После вероятностей составители ЕГЭ 2023 по профильной математике решили поставить уравнения и выражения. Уравнения ожидаются не супер лёгкие, но вполне решаемые: будут корни, логарифмы и степени. В выражениях в демоверсии ЕГЭ встретилась тригонометрия и степени.

7 задание

Ура, 7 задание осталось на своём месте: это задание с графиком и производными. Почему-то его не объединили в общий блок с 11 заданием, тоже посвящённым производным.

Далее в разборе демоверсии ЕГЭ 2023 по профильной математике выпускников ждут две задачи.

8 задание

8 задача на подстановку: нужно подставить в формулу известные числа и вычислить какую-либо величину. Ничего сложного, главное внимательность.

9 задание

Ещё одна текстовая задача. Здесь могут встретиться темы «Движение по прямой», «Движение по окружности», «Движение по реке» и «Сплавы, смеси, растворы». Такие задачи считаются не самыми простыми. Вместе с Эйджеем разберём этот номер в Телеграме.

10 задание

10 задание в демо ЕГЭ 2023 — «новое старое задание». Этот тип заданий с графиком впервые появился в 2022 году, и в КИМ 2023 попал без изменений. Возможно, стоит ждать усложнения этого задания.

11 задание

Традиционное задание с производными и точками минимума и максимума, которое почему-то не объединили в блок с другим заданием на производные.

Итак, обобщим всё, что мы узнали про первую часть демоверсии ЕГЭ по математике: в 2023 году в экзамене не появились ни вектора, ни комплексные числа. Можно немного расслабиться! Осталось выучить новую нумерацию, и всё будет хорошо.

Нумерация второй части в демоверсии ЕГЭ 2023 осталась без изменений, и это радует: не придётся переучивать номера и переживать. Посмотрим, что приготовили составители в этом году.

12 задание

Традиционно в разборе демоверсии ЕГЭ 2023 по профильной математике в 12 задании выпускников ждёт тригонометрическое уравнение.

13 задание

В 13 задании осталась стереометрия: в демоверсии представлена треугольная призма.

14 задание

В 14 задании всё по плану, там остались неравенства с логарифмами, ничего нового.

Это задание вместе с 12-ым составляет «джентльменский набор» из второй части — их под силу решить каждому, и этому нужно обязательно научиться, чтобы набрать 70+ баллов за ЕГЭ по профильной математике.

15 задание

15 задание также считается вполне решаемым. В демоверсии это экономическая задача про человека, который взял кредит в банке и рассчитывает выплаты и проценты.

16 задание

В задании 16 демоверсии ЕГЭ 2023 представлена планиметрическая задача про две окружности.

17 задание

Задача на параметр. Как показывает практика прошлых лет, параметр — самое решаемое задание из сложных заданий ЕГЭ.

18 задание

Задача на целые числа. Из трёх пунктов, А и Б решить может каждый, если хорошо подготовиться.

Чтобы получить 80+ баллов по профильной математике, нужно без ошибок решить первую часть и выполнить 12, 14, 15 и 18аб задания. А планиметрия, стереометрия, параметр и 18 задание полностью помогут получить заветную сотку. Как повысить свои шансы на успешную сдачу ЕГЭ по математике, рассказали в нашей статье.

Мы разобрали демоверсию ЕГЭ 2023 по математике, и теперь вы знаете, что приготовили для вас составители экзамена. Можно смело начинать подготовку! Эйджей уже составил план занятий и ждёт вас на курсе «Основа». Это возможность разобраться во всех темах и набить руку в решении заданий в компании единомышленников и с личным наставником.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Источник

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен 90^circ , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

$AC=frac{BC}{tgA}=frac{15}{0,75}=20.$

Ответ: 20.

2. B треугольнике ABC угол C равен $90^circ, , tgA=frac{9}{40}, , AC=20$ . Найдите AB.

По определению косинуса угла, $cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.$

Найдем косинус угла A с помощью формулы:

${tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.$

Отсюда ${cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.$

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен 58^circ , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, ${ S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}$ . Получим:

$S=frac{1}{2}cdot 10^2 cdot sin30^circ=25$ см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают 90^circ . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

$angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.$

8. B треугольнике ABC угол A равен 60^circ угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен $frac{1}{2}cdot (180^circ -x)$ .

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

$2x=frac{1}{2}cdot (180^circ -x).$
Отсюда ${x }= 36^circ.$

Ответ: 36.

Параллелограмм

10. B параллелограмме ABCD AB=3, AD=21, $sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

$DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.$

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b) , его площадь равна ab, а квадрат диагонали равен

Получим: , тогда a+b = 4 ,

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали AC = 3.

Ответ: 3.

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, $HG = EF = frac{5}{2}.$

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны $frac{5}{2}.$ Тогда HGFE — ромб, и его периметр равен $4cdot frac{5}{2}=10$ .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: $AH=frac{AB-CD}{2}=frac{26-14}{2}=6.$

Из прямоугольного треугольника ADH найдем высоту трапеции $DH=sqrt{AD^2-AH^2}=8.$

Площадь трапеции равна произведению полусуммы оснований на высоту:

$S=frac{left ( AB+CD right )cdot DH}{2}=160.$

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

$OF=FC=frac{1}{2}DC,$

$OE=AE=frac{1}{2}AB.$

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

Ответ: 40.

19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Ответ: 59.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ , и тогда угол ОBA равен Угол ОAB также равен 58^circ , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

Ответ: 64.

21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника $S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.$

Тогда

$r=frac{2cdot 12}{16}=frac{3}{2}=1,5.$

Ответ: 1,5.

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

Периметр треугольника:

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

Угол C может быть равен 30^circ или — ведь синусы этих углов равны $frac{1}{2}.$ Однако по рисунку угол C — острый, значит, он равен

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

По условию, угол C — тупой. Значит, он равен

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=frac{a+b-c}{2}.$ Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

$newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.$

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10 , CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен $frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.$

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ . Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

$angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.$

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

ИЛИ

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Задание 8

Задание 9

Задание 10

Задание 11

Задание 12

Задание 13

Задание 14

Задание 15

Задание 16

Задание 17

Задание 18

Что изменилось в ЕГЭ 2023 по профильной математике

1, 2 задания

3, 4 задания

8 задание

9 задание

11 задание

12 задание

13 задание

14 задание

15 задание

16 задание

17 задание

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://bez-smenki.ru/wp-content/uploads/2022/08/image31.png" alt width="1280" height="711" /> 18 задание

18 задание