Разбор пробного егэ по математике 2022 - Помощь в подготовке к экзаменам и поступлению

Московский пробник ЕГЭ по математике 23.04.2022 полный разбор.

Ссылка на вариант

Друзья, я допустил ошибку во втором решение задачи 10.2 Ошибка в 3 и 4 кругах.

Нам нужно, чтобы первый попал в первые 16 человек из 20 в каждом из двух кругов.

Вероятность такого события 16/20=4/5.

Вероятность встречи Ивана и Алексея в 3 круге — 4/5*4/19*1/16

Вероятность встречи Ивана и Алексея в 4 круге — 4/5*8/19*1/64

Поэтому верная сумма такая — 1/19 + 2/19*1/4 + 4/5*4/19*1/16 + 4/5*8/19*1/64 + 64/190*1/64 = 1/10

Источник

10 сентября 2021

В закладки

Обсудить

Жалоба

Разбор всех заданий проекта демоверсии 2022.

Задачи 1-13

Задание №1 — 6:28
Задание №2 — 10:05
Задание №3 — 14:50
Задание №4 — 18:10
Задание №5 — 22:30
Задание №6 — 26:56
Задание №7 — 32:12
Задание №8 — 38:48
Задание №9 — 41:38
Задание №10 — 45:56
Задание №11 — 48:30
Задание №12 — 50:46
Задание №13 — 58:33

Задачи 14-21

Задание №14 — 0:35
Задание №15 — 09:45
Задание №16 — 11:47
Задание №17 — 25:21
Задание №18 — 30:36
Задание №19- 35:40
Задание №20 — 47:50
Задание №21 — 56:36

Автор: Matesha Plus — Татьяна Колесникова.

Источник: youtube.com/c/MateshaPlus

Источник

: ЕГЭ по математике профиль

Разбор демоверсии ЕГЭ 2022 по математике.

Обзор демоверсий базового и профильного ЕГЭ-2022 по математике провел С. Ю. Кулабухов – зам. ген. директора по научной работе, кандидат физико- математических наук.

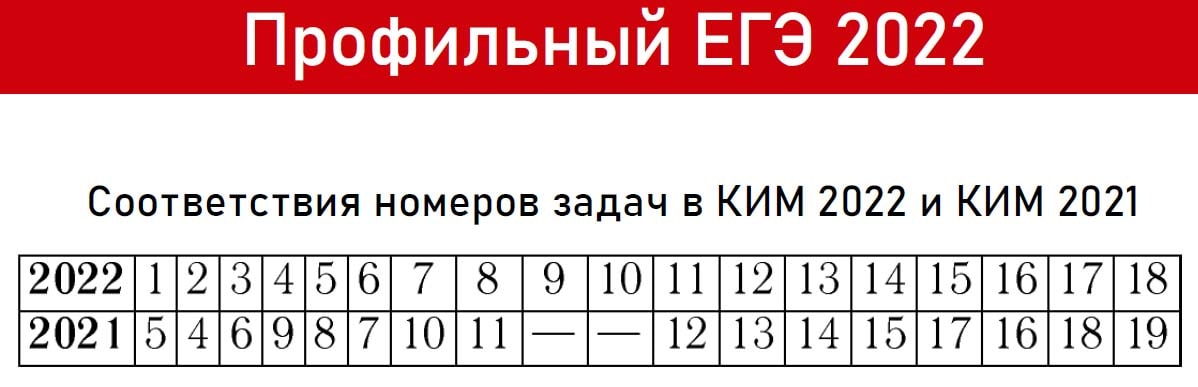
Соответствия номеров задач КИМ 2022 и КИМ 2021

Некоторые задания из демоверсии:

1. В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

2. Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?

3. Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?

4. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером»

Связанные страницы:

Источник

Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться в 2021-2022 учебном году к ЕГЭ по профильной математике.

В конце августа ФИПИ опубликовал проекты демонстрационных вариантов ЕГЭ 2022 года. Какие же изменения внесли разработчики ФИПИ в демо по профильной математике? Количество заданий сократилось до 18. Исключены старые задания 1-3. Добавлены новые задания №9 и №10 (моделирование реальных ситуаций на языке теории вероятностей и статистики, вычисление в простейших случаях вероятности событий). Задание №13 теперь оценивается в 3 максимальных балла, а № 15 — до 2 баллов. Максимальный первичный балл в новой демоверсии — 31.

Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.

Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репититорами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.

Разбор демоверсии ЕГЭ по профильной математике 2022 года с сайта ФИПИ

Источник: fipi.ru

Этат статья на Яндекс.Дзене: https://zen.yandex.ru/media/lancmanoge/razbor-demoversii-ege-po-profilnoi-matematike-2022-goda-613b32680658e02213fc1e12

Если материал показался интересным, подписывайтесь на обновления нашего блога. Мы знаем о поступлении в вузы всё (и даже больше). Кнопку подписки вы найдёте прямо под постом.

Рассылка «Lancman School»

Мы отправляем нашу интересную и очень полезную рассылку
два раза в неделю: во вторник и пятницу

Задание 1

Решите уравнение: $$4^x-2^x-2=0$$

Ответ: 1

Скрыть

$$4^x-2^x-2=0$$

$$2^2x-2^x-2=0$$

$$2^x=t, t>0$$

$$t^2-t-2=0$$

$$t=-1$$ и $$t=2$$

$$2^x=-1$$

$$varnothing$$

$$2^x=2$$

$$x=1$$

Задание 2

Лампочки выпускают только два завода. На первом заводе выпускают 20 % таких лампочек, остальные — на втором заводе. Вероятность того, что случайно выбранная лампочка с первого завода окажется бракованной, равна 0,025, а со второго завода — 0,015. Найдите вероятность того, что случайно выбранная такая лампочка бракованная.

Ответ: 0,017

Скрыть

$$P(л.б.)=P(л.б., з.1)+P(л.б., з.2)=0,025cdot0,2+0,015cdot0,8=0,017$$

Задание 3

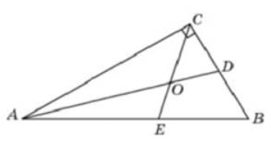
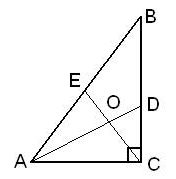
Острый угол прямоугольного треугольника равен 32°. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Ответ: 61

Скрыть

Острый угол пересечения биссектрис можно найти по формуле:

$$angle AOE=frac{1}{2}(angle A+angle C)=frac{90^{circ}+32^{circ}}{2}=61^{circ}.$$

Задание 4

Найдите $$frac{g(6-x)}{g(6+x)},$$ если $$g(x)=sqrt[11]{x(12-x)},$$ при $$|x|neq6$$

Ответ: 1

Скрыть

$$g(6-x)=sqrt[11]{(6-x)(12-(6-x))}=sqrt[11]{(6-x)(6+x)}$$

$$g(6+x)=sqrt[11]{(6+x)(12-(6+x))}=sqrt[11]{(6+x)(6-x)}$$

$$frac{g(6-x)}{g(6+x)}=frac{sqrt[11]{(6-x)(6+x)}}{sqrt[11]{(6+x)(6-x)}}=1$$

Задание 5

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны $$frac{2}{pi}.$$ Найдите объём цилиндра, описанного около этой призмы.

Ответ: 4

Скрыть

$$D=sqrt{a^2+a^2}=sqrt{2a^2}=asqrt{2}=2sqrt{2}$$

$$V=frac{pi D^2}{4}cdot H=frac{picdot4cdot2}{4}cdotfrac{2}{pi}=4$$

Задание 6

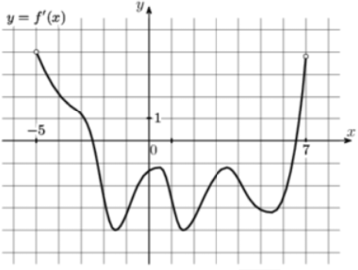
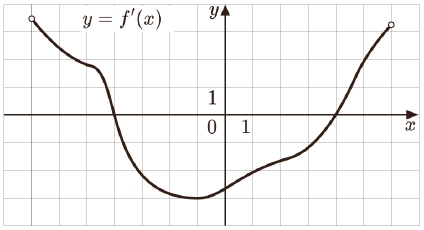
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x)$$ определенной на интервале $$(-5;7).$$ Найдите промежутки убывания функции $$f(x).$$ В ответе укажите сумму целых точек, входящих в эти промежутки.

Ответ: 18

Скрыть

Функция убывает там, где $$f'(x)<0,$$ т.е. график производной под $$Ox$$: тогда целые от $$-2$$ до $$6$$ включительно.

$$-2-1+0+1+2+3+4+5+6=18$$

Задание 7

Скорость колеблющегося на пружине груза меняется по закону $$v(t)=5sin(pi t)$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Ответ: 0,67

Скрыть

$$5sinpi tgeq2,5$$

$$sinpi tgeq0,5$$

$$frac{pi}{6}+2pi nleqpi tleqfrac{5pi}{6}+2pi n$$

Так как просят в течении первой секунды, то $$n=0$$

$$frac{1}{6}leq tleqfrac{5}{6}$$

$$tau=frac{frac{5}{6}-frac{1}{6}}{1}=frac{2}{3}approx0,67$$

Задание 8

Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.

Ответ: 18

Скрыть

Пусть $$a_1=10$$ км прошел турист в первый день;

$$n = 6$$ дней,

$$a_3$$ – в третий день,

$$a_6$$ – в последний ($$n$$-ый) день.

Тогда за 6 дней турист прошел 120 км.

$$S_n=frac{(a_1+a_n)n}{2}$$

$$120=frac{(10+a_6)6}{2}$$

$$frac{120}{3}=10+a_6$$

$$a_n=a_1+(n-1)d$$

$$30=10+(6-1)d$$

$$d=4$$ км — ежедневная прибавка

$$a_3=10+(3-1)4=18$$ км — в третий день

Задание 9

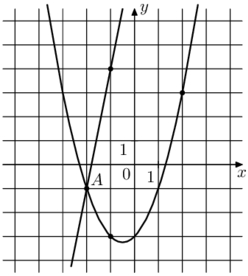
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Ответ: 1,2

Скрыть

Первая прямая проходит через $$(2;-1)$$ и $$(3;1).$$

Тогда: $$left{begin{matrix} -1=2k+b\ 1=3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} -1=4+b\ 2=k end{matrix}right.Leftrightarrowleft{begin{matrix} b=-5\ k=2 end{matrix}right.$$

Получим: $$y=2x-5.$$

Вторая проходит через точки $$(0;1)$$ и $$(1;-2).$$

Тогда: $$left{begin{matrix} 1=0cdot k+b\ -2=1cdot k+b end{matrix}right.Leftrightarrowleft{begin{matrix} b=1\ k=-3 end{matrix}right.$$

Получим: $$y=-3x+1.$$

Тогда: $$2x-5=-3x+1Leftrightarrow 5x=6Leftrightarrow x=1,2$$

Задание 10

Монету подбрасывают до тех пор, пока орёл не выпадет два раза (не обязательно подряд). Найдите математическое ожидание числа бросков.

Ответ: 4

Скрыть

Если сделано 2 броска, то общее количество исходов 4 штуки (ОО; ОР; РО; РР) и только один с двумя орлами, то есть $$frac{1}{4}$$ — вероятность 2 орлов за 2 броска.

Далее за 3 считаем: всего исходов 8, с 2 орлами 3 (ООР; ОРО; РОО), но ООР мы не считаем, так как если бы первыми двумя бросками выпали орлы, то третий не делали бы. Значит $$2Rightarrow P=frac{2}{8}=frac{1}{4}.$$

За 4 броска: всего 16 исходов, 2 орла: ОРРО; РОРО; РРОО (такие как ООРР или РООР исключаем). Итого $$P=frac{3}{8}.$$

И так далее. Получается:

Кол-во бросков	1	2	3	4	5	…	n
Вероятность	0	$$0,5^2$$	$$2cdot0,5^3$$	$$3cdot0,5^4$$	$$4cdot0,5^5$$	…	$$(n-1)cdot0,5^n$$

При этом математическое ожидание есть сумма всех произведений количества бросков на соответствующую вероятность:

$$M(x)=sum^{infty}_{n=2}ncdotfrac{n-1}{2^n}=4$$

Задание 11

Найдите точку максимума функции $$y=(2x-3)cos x-2sin x+5,$$ принадлежащую промежутку $$(0;frac{pi}{2}).$$

Ответ: 1,5

Скрыть

$$y’ = (2x – 3)’·cos x + (2x – 3)·(cos x)’ – (2sin x)´$$

$$y’ = 2cos x – (2x – 3)sin x – 2cos x = – (2x – 3)sin x$$

$$y’ = – (2x – 3)sin x$$

$$y’ = 0$$

$$– (2x – 3)sin x = 0$$

$$(3 – 2x)sin x = 0$$

$$3 – 2x = 0$$ и $$sin x = 0$$

Решим 1 уравнение:

$$3 – 2x = 0$$

$$x = frac{3}{2}$$

$$x = 1,5$$

Решим 2 уравнение:

$$sin x = 0$$

$$x = 0$$ не принадлежит промежутку $$(0;frac{pi}{2})$$

Отметим точку $$x = 1,5$$ на числовой прямой, учитывая промежуток $$(0;frac{pi}{2})$$ и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)

В точке $$x = 1,5$$ производная функции меняет знак с положительного на отрицательный, значит, это искомая точка максимума.

Задание 12

А) Решите уравнение $$frac{2sin^2x-sin x-1}{log_2(cos x)}=0$$

Б) Найдите все корни уравнения, принадлежащие отрезку $$[pi;frac{5pi}{2}]$$

Ответ: А)$$-frac{pi}{6}+2pi n,nin Z$$ Б)$$frac{11pi}{6}$$

Задание 13

В прямоугольном параллелепипеде $$ABCDA_1B_1C_1D_1$$ известны ребра $$ВС=5$$ и $$АВ=АА_1=8,$$ M и N — середины ребер $$CD$$ и $$АА_1$$ соответственно. Плоскость $$alpha$$ проходит через точки $$М$$ и $$В$$ и параллельна прямой $$CD_1.$$

А) Докажите, что прямая $$DN$$ параллельна плоскости $$alpha$$

Б) Найдите расстояние между прямыми $$C_1D$$ и $$BD_1$$

Ответ: $$frac{20sqrt{34}}{51}$$

Задание 14

Решите неравенство: $$2xgeqlog_2(frac{35}{3}cdot6^{x-1}-2cdot9^{x-frac{1}{2}})$$

Ответ: $$(-infty;-1],[2;log_{1,5}frac{35}{12})$$

Задание 15

В июле 2022 года планируется взять кредит в банке на некоторую сумму сроком на 5 лет. Условия возврата таковы:

— в январе долг возрастает на 10% по сравнению с концом предыдущего года;

— с февраля по июнь необходимо внести единым платежом часть долга;

— в июле 2023, 2024 годов долг должен быть на одну и ту же сумму меньше долга июля предыдущего года;

— в июле 2024 года долг составляет 80% от первоначальной суммы кредита;

— выплаты в 2025 и 2026 годах равны по 202 тыс. рублей;

— долг в июле 2026 года составляет 20% от суммы долга на июль 2024 года;

— в июле 2027 года долг должен быть полностью погашен.

Определите, чему равна общая сумма выплат.

Ответ: 701,15 тыс. руб.

Задание 16

В равнобедренной трапеции ABCD угол BCD — тупой. Через точку В проведена прямая, параллельная прямой CD и пересекающая прямую AD в точке Е. На продолжении ВЕ за точку Е отмечена точка F такая, что DE=DF.

А) Докажите, что точки A, F, C и D лежат на одной окружности.

Б) Найдите расстояние от точки С до прямой AF, если $$BD=10$$ и $$cosangle ADC = 0,6$$

Ответ: 8

Задание 17

Найдите все значения параметра $$a,$$ при каждом из которых уравнение

$$sqrt{x-2a}+sqrt{x^2+4ax+4a^2}=2$$

имеет хотя бы одно решение

Ответ: $$[-1;frac{1}{2}]$$

Задание 18

Составим две последовательности натуральных чисел $$left{a_nright}$$ и $$left{b_nright}.$$

$$a_1 = 1, a_n =frac{n}{p} (n > 1),$$ где $$p$$ — наименьший простой делитель числа $$n.$$

$$b_1 = 1, b_n (n > 1)$$ — количество таких чисел $$m,$$ для которых $$a_m = n.$$ Оно показывает, сколько раз число $$n$$ встречается в последовательности $$left{a_nright}.$$

А) Найдите $$b_187.$$

Б) Для каких чисел $$n > 1$$ и $$m > 1$$ выполняется равенство $$b_n= b_m?$$

В) Чему равно $$b_m,$$ если $$m = 8n^3+12n^2- 2n-3?$$

(Автор задачи Сергей Андреевич Тюрин)

Ответ: А) 5, Б) числа n и m должны иметь одинаковый наименьший простой делитель, В) 2

Источник

Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

Задание 1.
Найдите корень уравнения log₂(7 – x) = 5.

Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.

ИЛИ

В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Задание 3.
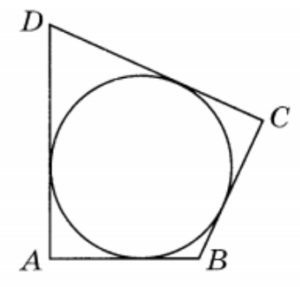
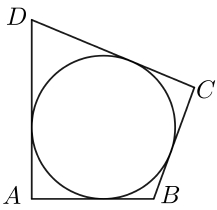
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.

ИЛИ

В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.

Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}

ИЛИ

Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}

Задание 5.
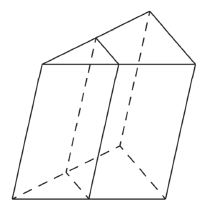
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

ИЛИ

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.

Задание 6.
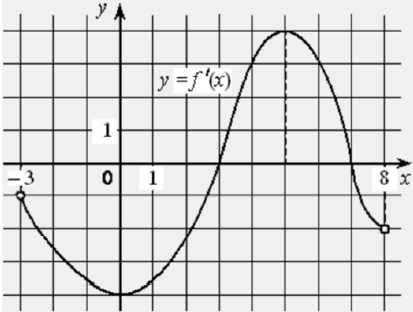
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).

ИЛИ

На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).

Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: f=f_{0}cdot frac{c+u}{c-v}, где f₀ = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.

ИЛИ

В розетку электросети подключены приборы, общее сопротивление которых составляет R₁ = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R₂ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R₁ Ом и R₂ Ом их общее сопротивление дается формулой R_{общ}=frac{R_{1}R_{2}}{R_{1}+R_{2}} (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.

Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

ИЛИ

Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Задание 9.
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax² + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

ИЛИ

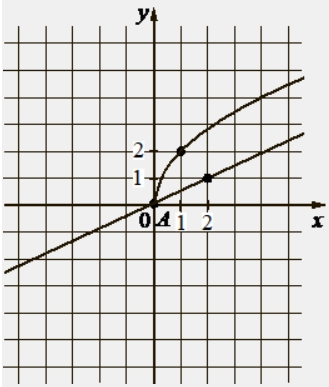
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.

Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

ИЛИ

Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 11.
Найдите точку минимума функции y = frac{4}{3}xsqrt{x}-5x+4.

Задание 12.
а) Решите уравнение 4^{sin x} + 4^{sin(x + π)} = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].

Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.

Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1

Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?

Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.

Задание 17.
Найдите всe значения параметра a, при каждом их которых система

begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, \ y=ax. end{cases}

имеет ровно 3 различных решения.

Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?

Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.7 / 5. Количество оценок: 19

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Разбор демоверсии ЕГЭ по профильной математике 2022 года с сайта ФИПИ

Рассылка «Lancman School»

Похожие статьи:

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Задание 8

Задание 9

Задание 10

Задание 11

Задание 12

Задание 13

Задание 14

Задание 15

Задание 16

Задание 17

Задание 18