В данном разделе мы занимаемся подготовкой к ЕГЭ по математике как базового, профильного уровня — у нас представлены разборы задач, тесты, описание экзамена и полезные рекомендации. Пользуясь нашим ресурсом, вы как минимум разберетесь в решении задач и сможете успешно сдать ЕГЭ по математике в 2020 году. Начинаем!
ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида — базовый и профильный. В данном разделе я приведен разбор каждого вида заданий с подробным объяснением для двух вариантов. Задания ЕГЭ строго тематические, поэтому для каждого номера можно дать точные рекомендации и привести теорию, необходимую именно для решения данного вида задания. Ниже вы найдете ссылки на задания, перейдя по которым можно изучить теорию и разобрать примеры. Примеры постоянно пополняются и актуализируются.
Структура базового уровня ЕГЭ по математике
Экзаменационная работа по математике базового уровня состоит из одной части, включающей 20 заданий с кратким ответом. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Ответом к каждому из заданий 1–20 является целое число, конечная десятичная дробь, или последовательность цифр.
Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.
Разбор заданий ЕГЭ по математике (база)
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
Каким был ЕГЭ по математике в 2022 году?
Мы знаем, что в 2022 году формат ЕГЭ по математике изменился. Поменялась нумерация заданий. Добавились новые задачи: №9 (Функции и графики) и № 10 (Теория вероятностей). И в первой части стало на 1 задачу меньше.
Во второй части ЕГЭ также произошли изменения.
«Экономическая» задача, которая теперь под № 15, оценивается уже не в 3, а только в 2 первичных балла.
А вот задача по стереометрии, №13, наоборот, «подорожала» и теперь оценивается в 3 балла.
Расскажем о заданиях 2 части ЕГЭ, задачах 13-18, а затем подробно разберем различные типы таких задач.
Задание 12, уравнения. Все стандартно, просто тригонометрия.
Задание 13, стереометрия. По сравнению с прошлыми годами сложность значительно выше. Здесь и теорема Менелая, и произвольная призма, и пересечение сфер.
Задача 14, неравенство. Все стандартно – показательное неравенство, замена переменной. Помним о секретах решения таких задач! Сделав замену, сначала полностью решаем неравенство для новой переменной, затем возвращаемся к первоначальной.
Задача 15, экономическая. В 2022 году были только кредиты и вклады. Обошлись без задач на оптимизацию.
Задача 16, планиметрия. Простые задания, без затей. Подобные треугольники, теорема косинусов, свойство биссектрисы треугольника, в общем, обязательная школьная программа по геометрии.
Задание 17, задачи с параметрами. Составители вариантов порадовали разнообразием: был и графический метод, и аналитический. И решение квадратных уравнений с параметрами. И в каждом задании присутствовали модули, так что кто эту тему не знает, надо повторить!
Изучить «параметры» с нуля можно с помощью Видеокурса Анны Малковой
Полный курс, 26 часов видео, 13 видеоуроков. 11 методов решения задач с параметрами.
И наконец, задание 18, задачи на числа и их свойства. Все типы заданий – новые, нестандартные. Числа на круге, использование делимости и остатков.
Освоить эту необычную задачу можно с помощью видеокурса Анны Малковой.
Полный курс, 10 видеоуроков по 2 часа. 11 методов решения задач на числа и их свойства.
А теперь подробно о каждом задании ЕГЭ-2022, 2 часть.
Уравнения на EГЭ -2022 по математике, задача 12
Cтереометрия на EГЭ-2022 по математике, задача 13
Hеравенства на EГЭ-2022 по математике, задача 14
Экономические задачи и финансовая математика на ЕГЭ-2022, задача 15
Планиметрия на EГЭ-2022 по математике, задача 16
Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения
Задача 18 на числа и их свойства на ЕГЭ-2022 по математике
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ЕГЭ-2022, математика. Все задачи с решениями» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).

«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».
Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1.
В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#
Задание № 2 проверяет умение читать диаграммы.
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?
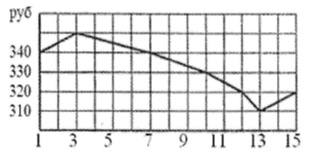
Решение:
1) 340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.
2) 1000 · 3/4 = 750 (акций) — составляют 3/4 от всех купленных акций.
3) 330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.
4) 1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.
5) 310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.
6) 247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.
Ответ: 15000.
Задание № 3 — является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.
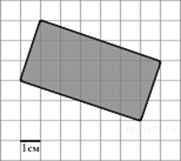
Пример 3. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение: Для вычисления площади данной фигуры можно воспользоваться формулой Пика:
|
На рисунке справа B = 7 (красные точки), Г = 8 (зелёные точки),
Для вычисления площади данного прямоугольника воспользуемся формулой Пика: где В = 10, Г = 6, поэтому Ответ: 20. |
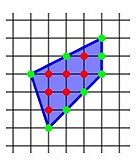
|
Читайте также: ЕГЭ по физике: решение задач о колебаниях
Задание № 4 — задача курса «Теория вероятностей и статистика». Проверяется умение вычислять вероятность события в простейшей ситуации.
Пример 4. На окружности отмечены 5 красных и 1 синяя точка. Определите, каких многоугольников больше: тех, у которых все вершины красные, или тех, у которых одна из вершин синяя. В ответе укажите, на сколько одних больше, чем других.
Решение: 1) Воспользуемся формулой числа сочетаний из n элементов по k:
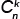 = =
|
n! | . |
| k!(n – k)! |
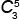 = =
|
5! | = | 3! · 4 · 5 | = | 4 · 5 | = 10 треугольников, |
| 3!(5 – 3)! | 3!2! | 1 · 2 |
у которых все вершины красные.
2)
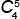 = =
|
5! | = | 4! · 5 | = 5 треугольников, |
| 4!(5 – 4)! | 4!1! |
у которых все вершины красные.
3) Один пятиугольник, у которого все вершины красные.
4) 10 + 5 + 1 = 16 многоугольников, у которых все вершины красные.
5)
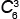 = =
|
6! | = | 3! · 4 · 5 · 6 | = | 4 · 5 · 6 | = 20 треугольников, |
| 3!(6 – 3)! | 3!3! | 1 · 2 · 3 |
у которых вершины красные или с одной синей вершиной.
6)
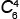 = =
|
6! | = | 4! · 5 · 6 | = | 5 · 6 | = 15 четырёхуголников, |
| 4!(6 – 4)! | 4!2! | 1 · 2 |
у которых вершины красные или с одной синей вершиной.
7)
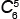 = =
|
6! | = | 5! · 6 | = 6 пятиугольников, |
| 5!(6 – 5)! | 5!1! |
у которых вершины красные или с одной синей вершиной.

9) 20 + 15 + 6 + 1 = 42 многоуголника, у которых все вершины красные или с одной синей вершиной.
10) 42 – 16 = 26 многоугольников, в которых используется синяя точка.
11) 26 – 16 = 10 многоугольников – на сколько многоугольников, у которых одна из вершин — синяя точка, больше, чем многоугольников, у которых все вершины только красные.
Ответ: 10.
Задание № 5 — базового уровня первой части проверяет умения решать простейшие уравнения (иррациональные, показательные, тригонометрические, логарифмические).
Пример 5. Решите уравнение 23 + x = 0,4 · 53 + x.
Решение. Разделим обе части данного уравнения на 53 + х ≠ 0, получим
| 23 + x | = 0,4 или |
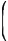
|
2 |

|
3 + х | = | 2 | , |
| 53 + х | 5 | 5 |
откуда следует, что 3 + x = 1, x = –2.
Ответ: –2.
Задание № 6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.
Пример 6. Площадь треугольника ABC равна 129. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
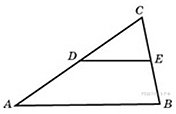
Решение. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол СDE равен углу CAB как соответственные углы при DE || AB секущей AC. Так как DE – средняя линия треугольника по условию, то по свойству средней линии | DE = (1/2)AB. Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
| SΔCDE | = |
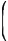
|
2 |

|
2 | ; SΔCDE = | 1 | · 129 = 32,25. |
| SΔCAB | 5 | 4 |
Следовательно, SABED = SΔABC – SΔCDE = 129 – 32,25 = 96,75.
Ответ: 96,75.
Смотреть вебинары по алгебре
Задание № 7 — проверяет применение производной к исследованию функции. Для успешного выполнения необходимо содержательное, не формальное владение понятием производной.
Пример 7. К графику функции y = f(x) в точке с абсциссой x0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; –1) этого графика. Найдите f′(x0).
Решение. 1) Воспользуемся уравнением прямой, проходящей через две заданные точки и найдём уравнение прямой, проходящей через точки (4; 3) и (3; –1).
(y – y1)(x2 – x1) = (x – x1)(y2 – y1)
(y – 3)(3 – 4) = (x – 4)(–1 – 3)
(y – 3)(–1) = (x – 4)(–4)
–y + 3 = –4x + 16| · (–1)
y – 3 = 4x – 16
y = 4x – 13, где k1 = 4.
2) Найдём угловой коэффициент касательной k2, которая перпендикулярна прямой y = 4x – 13, где k1 = 4, по формуле:
| k1 · k2 = –1, k2 = | –1 | –0,25. |
| 4 |
3) Угловой коэффициент касательной – производная функции в точке касания. Значит, f′(x0) = k2 = –0,25.
Ответ: –0,25.
Задание № 8 — проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.
Пример 8. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
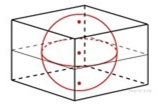
Решение. 1) Vкуба = a3 (где а – длина ребра куба), поэтому
а3 = 216
а = 3√216
a = 6.
2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = a, d = 6, d = 2R, R = 6 : 2 = 3.
Ответ: 3.
Приемы подготовки к профильному ЕГЭ по математике
Задание № 9 — требует от выпускника навыков преобразования и упрощения алгебраических выражений. Задание № 9 повышенного уровня сложности с кратким ответом. Задания из раздела «Вычисления и преобразования» в ЕГЭ подразделяются на несколько видов:
-
преобразования числовых рациональных выражений;
-
преобразования алгебраических выражений и дробей;
-
преобразования числовых/буквенных иррациональных выражений;
-
действия со степенями;
-
преобразование логарифмических выражений;
- преобразования числовых/буквенных тригонометрических выражений.
Пример 9. Вычислите tgα, если известно, что cos2α = 0,6 и
Решение. 1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos2α – 1 и найдём
| cos2α = | cos2α + 1 | = | 0,6 + 1 | = | 1,6 | = 0,8. |
| 2 | 2 | 2 |
2) Воспользуемся формулой тригонометрических функций одного угла:
и найдём
| tg2α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos2α | 0,8 | 8 | 4 | 4 | 4 |
Значит, tg2α = ± 0,5.
3) По условию
значит, α – угол II четверти и tgα < 0, поэтому tgα = –0,5.
Ответ: –0,5.
#ADVERTISING_INSERT#
Задание № 10 — проверяет у учащихся умение использовать приобретенные раннее знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен получиться в виде целого числа или конечной десятичной дроби.
Пример 10. Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q = mv2sin2α. Под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение. Для решения задачи нам необходимо решить неравенство Q ≥ 50, на интервале 2α ∈ (0°; 180°).
mv2sin2α ≥ 50
2· 102sin2α ≥ 50
200 · sin2α ≥ 50
Решением данного неравенства являются два неравенства:
| sinα ≥ | 1 | и sinα ≤ – | 1 | . |
| 2 | 2 |
Так как α ∈ (0°; 90°), то будем решать только
Неравенство
мы не рассматриваем, так как α для него будет более 180°. Итак:
Изобразим решение неравенства графически:
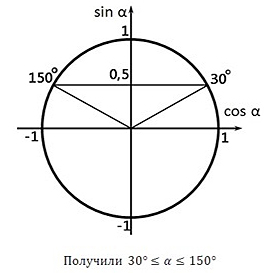
Так как по условию α ∈ (0°; 90°), значит 30° ≤ α < 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.
Ответ: 60.
Скачать бесплатно рабочие программы по алгебре
Задание № 11 — является типовым, но оказывается непростым для учащихся. Главным источником затруднений является построение математической модели (составление уравнения). Задание № 11 проверяет умение решать текстовые задачи.
Пример 11. На весенних каникулах 11-классник Вася должен был решить 560 тренировочных задач для подготовки к ЕГЭ. 18 марта в последний учебный день Вася решил 5 задач. Далее ежедневно он решал на одно и то же количество задач больше по сравнению с предыдущим днём. Определите, сколько задач Вася решил 2 апреля в последний день каникул.
Решение:
Обозначим a1 = 5 – количество задач, которые Вася решил 18 марта, d – ежедневное количество задач, решаемых Васей, n = 16 – количество дней с 18 марта по 2 апреля включительно, S16 = 560 – общее количество задач, a16 – количество задач, которые Вася решил 2 апреля. Зная, что ежедневно Вася решал на одно и то же количество задач больше по сравнению с предыдущим днём, то можно использовать формулы нахождения суммы арифметической прогрессии:
560 = (5 + a16) · 8,
5 + a16 = 560 : 8,
5 + a16 = 70,
a16 = 70 – 5
a16 = 65.
Значит, Вася решил 2 апреля 65 задач.
Ответ: 65.
Задание № 12 — проверяют у учащихся умение выполнять действия с функциями, уметь применять производную к исследованию функции.
Пример 12. Найти точку максимума функции y = 10ln(x + 9) – 10x + 1.
Решение: 1) Найдем область определения функции: x + 9 > 0, x > –9, то есть x ∈ (–9; ∞).
2) Найдем производную функции:
3) Найдем нули производной:
| y′= 0, | 10 | – 10 = 0, x = –8. |
| x + 9 |
4) Найденная точка принадлежит промежутку (–9; ∞). Определим знаки производной функции и изобразим на рисунке поведение функции:
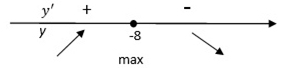
Искомая точка максимума x = –8.
Ответ: –8.
Скачать бесплатно рабочую программу по математике к УМК Мерзляка А.Г. 5-11 класс
Скачать бесплатно рабочую программу по математике к линии УМК Г.К. Муравина, К.С. Муравина, О.В. Муравиной 10-11
Скачать бесплатно методические пособия по алгебре
Задание № 13 — повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 13. а) Решите уравнение 2log32(2cosx) – 5log3(2cosx) + 2 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку 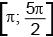
Решение: а) Пусть log3(2cosx) = t, тогда 2t2 – 5t + 2 = 0,
| откуда t = 2 или t = | 1 | . |
| 2 |

|
log3(2cosx) = | 2 | ⇔ |

|
2cosx = 9 | ⇔ |

|
cosx = | 4,5 | ⇔ т.к. |cosx| ≤ 1, |
| log3(2cosx) = | 1 | 2cosx = √3 | cosx = | √3 | ||||||
| 2 | 2 |

|
x = | π | + 2πk |
| 6 | |||
| x = – | π | + 2πk, k ∈ Z | |
| 6 |
б) Найдём корни, лежащие на отрезке 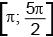
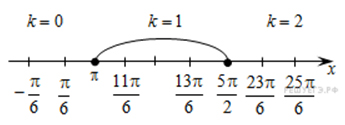
Из рисунка видно, что заданному отрезку принадлежат корни
| Ответ: а) | π | + 2πk; – | π | + 2πk, k ∈ Z; б) | 11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Задание № 14 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
Пример 14. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение: а) Хорда длиной 12 находится на расстоянии 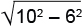

Тогда расстояние между хордами составляет либо
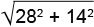
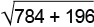
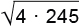
либо



По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.
б) Обозначим центры оснований за О1 и О2. Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание — H (H ∈ β). Тогда AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен
| ∠ABH = arctg | AH | = arctg | 28 | = arctg14. |
| BH | 8 – 6 |
Ответ: arctg 14.
Подготовка к ОГЭ и ЕГЭ для учителей по алгебре
Задание № 15 — повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 15. Решите неравенство |x2 – 3x| · log2(x + 1) ≤ 3x – x2.
Решение: Областью определения данного неравенства является интервал (–1; +∞). Рассмотри отдельно три случая:
1) Пусть x2 – 3x = 0, т.е. х = 0 или х = 3. В этом случае данное неравенство превращается в верное, следовательно, эти значения входят в решение.
2) Пусть теперь x2 – 3x > 0, т.е. x ∈ (–1; 0) ∪ (3; +∞). При этом данное неравенство можно переписать в виде (x2 – 3x) · log2(x + 1) ≤ 3x – x2 и разделить на положительное выражение x2 – 3x. Получим log2(x + 1) ≤ –1, x + 1 ≤ 2–1, x ≤ 0,5 –1 или x ≤ –0,5. Учитывая область определения, имеем x ∈ (–1; –0,5].
3) Наконец, рассмотрим x2 – 3x < 0, при этом x ∈ (0; 3). При этом исходное неравенство перепишется в виде (3x – x2) · log2(x + 1) ≤ 3x – x2. После деления на положительное выражение 3x – x2, получим log2(x + 1) ≤ 1, x + 1 ≤ 2, x ≤ 1. Учитывая область, имеем x ∈ (0; 1].
Объединяя полученные решения, получаем x ∈ (–1; –0.5] ∪ [0; 1] ∪ {3}.
Ответ: (–1; –0.5] ∪ [0; 1] ∪ {3}.
Задание № 16 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
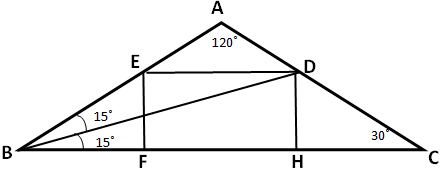
Пример 16. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.
Решение: а)
1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = 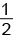
2) Пусть EF = DH = x, тогда BE = 2x, BF = x√3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.
BD – биссектриса ∠B, значит ∠ABD = ∠DBC = 15˚.
4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.
| tg 15° = tg(45° – 30°) = | 3 – √3 | , |
| 3 + √3 |
| 3 – √3 | , | x |
| 3 + √3 | x√3 + FH |
(x√3 + FH)(3 – √3) = x(3 + √3)
2√3x – 6x = √3FH – 3FH
2x(√3 – 3) = FH(√3 – 3)
FH = 2x
FH = 2DH
Что требовалось доказать.
б) 1) ΔAED ∼ ΔABC по двум углам, так как ∠B – общий, ∠AED = ∠ABC как соответственные при ED || BC секущей AB. Из подобия треугольников следует:
√3 – 1 = 2 – x
x = 3 – √3
EF = 3 – √3
2) SDEFH = ED · EF = (3 – √3) · 2(3 – √3)
SDEFH = 24 – 12√3.
Ответ: 24 – 12√3.
Задание № 17 — задание с развернутым ответом, это задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Это задание — текстовая задача с экономическим содержанием.
Пример 17. Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн. рублей, где х — целое число. Найдите наибольшее значение х, при котором банк за четыре года начислит на вклад меньше 17 млн рублей.
Решение: В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн рублей, а в конце второго – 22 + 22 · 0,1 = 24,2 млн рублей. В начале третьего года вклад (в млн рублей) составит (24,2 + х), а в конце — (24,2 + х) + (24,2 + х) · 0,1 = (26,62 + 1,1х). В начале четвёртого года вклад составит (26,62 + 2,1х), а в конце — (26,62 + 2,1х) + (26,62 + 2,1х) · 0,1 = (29,282 + 2,31х). По условию, нужно найти наибольшее целое х, для которого выполнено неравенство
(29,282 + 2,31x) – 20 – 2x < 17
29,282 + 2,31x – 20 – 2x < 17
0,31x < 17 + 20 – 29,282
0,31x < 7,718
Наибольшее целое решение этого неравенства — число 24.
Ответ: 24.
Задание № 18 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 18 необходим, кроме прочных математических знаний, также высокий уровень математической культуры.
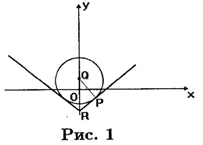
Пример 18. При каких a система неравенств
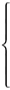 |
x2 + y2 ≤ 2ay – a2 + 1 |
| y + a ≤ |x| – a |
имеет ровно два решения?
Решение: Данную систему можно переписать в виде
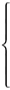 |
x2 + (y – a)2 ≤ 1 |
| y ≤ |x| – a |
Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y = |x| – a,причём последний есть график функции
y = |x|, сдвинутый вниз на а. Решение данной системы есть пересечение множеств решений каждого из неравенств.
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.
Точки касания круга с прямыми и будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит, треугольник PQR – прямоугольный равнобедренный. Точка Q имеет координаты (0, а), а точка R – координаты (0, –а). Кроме того, отрезки PR и PQ равны радиусу окружности, равному 1. Значит,
Перейти в каталог продукции по алгебре
Задание № 19 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 19 необходимо уметь осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы.
Пример 19. Пусть Sn сумма п членов арифметической прогрессии (ап). Известно, что Sn + 1 = 2n2 – 21n – 23.
а) Укажите формулу п-го члена этой прогрессии.
б) Найдите наименьшую по модулю сумму Sn.
в) Найдите наименьшее п, при котором Sn будет квадратом целого числа.
Решение: а) Очевидно, что an = Sn – Sn – 1. Используя данную формулу, получаем:
Sn = S(n – 1) + 1 = 2(n – 1)2 – 21(n – 1) – 23 = 2n2 – 25n,
Sn – 1 = S(n – 2) + 1 = 2(n – 1)2 – 21(n – 2) – 23 = 2n2 – 25n + 27
значит, an = 2n2 – 25n – (2n2 – 29n + 27) = 4n – 27.
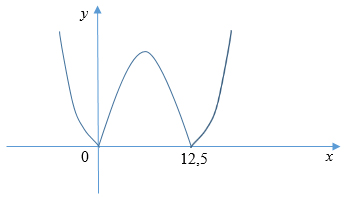
б) Так как Sn = 2n2 – 25n, то рассмотрим функцию S(x) = |2x2 – 25x|. Ее график можно увидеть на рисунке.
Очевидно, что наименьшее значение достигается в целочисленных точках, расположенных наиболее близко к нулям функции. Очевидно, что это точки х = 1, х = 12 и х = 13. Поскольку, S(1) = |S1| = |2 – 25| = 23, S(12) = |S12| = |2 · 144 – 25 · 12| = 12, S(13) = |S13| = |2 · 169 – 25 · 13| = 13, то наименьшее значение равно 12.
в) Из предыдущего пункта вытекает, что Sn положительно, начиная с n = 13. Так как Sn = 2n2 – 25n = n(2n – 25), то очевидный случай, когда данное выражение является полным квадратом, реализуется при n = 2n – 25, то есть при п = 25.
Осталось проверить значения с 13 до 25:
S13 = 13 · 1, S14 = 14 · 3, S15 = 15 · 5, S16 = 16 · 7, S17 = 17 · 9, S18 = 18 · 11, S19 = 19 · 13, S20 = 20 · 13, S21 = 21 · 17, S22 = 22 · 19, S23 = 23 · 21, S24 = 24 · 23.
Получается, что при меньших значениях п полный квадрат не достигается.
Ответ: а) an = 4n – 27; б) 12; в) 25.
Фото: nn.ucheba.ru
________________
*С мая 2017 года объединенная издательская группа «ДРОФА-ВЕНТАНА» входит в корпорацию «Российский учебник». В корпорацию также вошли издательство «Астрель» и цифровая образовательная платформа «LECTA». Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства «ДРОФА» в сфере цифрового образования (электронные формы учебников, «Российская электронная школа», цифровая образовательная платформа LECTA). До прихода в издательство «ДРОФА» занимал позицию вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». Сегодня издательская корпорация «Российский учебник» обладает самым крупным портфелем учебников, включенных в Федеральный перечень — 485 наименований (примерно 40%, без учета учебников для коррекционной школы). Издательствам корпорации принадлежат наиболее востребованные российскими школами комплекты учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые нужны для развития производственного потенциала страны. В портфель корпорации входят учебники и учебные пособия для начальной школы, удостоенные Премии Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример: