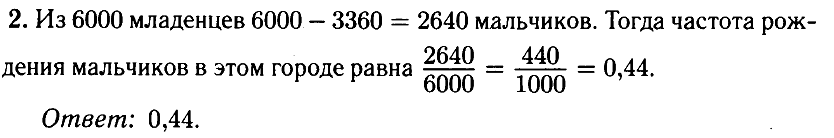Задание 3. Теория вероятностей на ЕГЭ по математике.
Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…
Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.
Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?
Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
Орел и решка — два возможных исхода испытания.
Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .
Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.
Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).
Вероятность четверки — тоже .
А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность не может быть больше единицы.
Вот другой пример. В пакете яблок, из них
— красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна
, а зеленое —
.
Вероятность достать красное или зеленое яблоко равна .
БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ
Определение вероятности. Простые задачи из вариантов ЕГЭ.
Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.
В фирме такси в данный момент свободно
машин:
красных,
желтых и
зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.
Всего имеется машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна
, то есть
.
В сборнике билетов по биологии всего
билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть
.
Родительский комитет закупил
пазлов для подарков детям на окончание учебного года, из них
с картинами известных художников и
с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.
Задача решается аналогично.
Ответ: .
В чемпионате по гимнастике участвуют
спортсменок:
— из России,
— из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —
спортсменок). Ответ:
.
Ученика попросили назвать число от
до
. Какова вероятность того, что он назовет число кратное пяти?
Каждое пятое число из данного множества делится на . Значит, вероятность равна
.
Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.
— нечетные числа;
— четные. Вероятность нечетного числа очков равна
.
Ответ: .
Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?
Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.
Как вы думаете, сколько здесь возможных исходов?
Бросаем монету. У этого действия два возможных исхода: орел и решка.
Две монеты — уже четыре исхода:
| орел | орел |
| орел | решка |
| решка | орел |
| решка | решка |
Три монеты? Правильно, исходов, так как
.
Вот они:
| орел | орел | орел |
| орел | орел | решка |
| орел | решка | орел |
| решка | орел | орел |
| орел | решка | решка |
| решка | орел | решка |
| решка | решка | орел |
| решка | решка | решка |
Два орла и одна решка выпадают в трех случаях из восьми.
Ответ: .
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет
очков. Результат округлите до сотых.
Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего возможных исходов, так как
.
А теперь — благоприятные исходы:
Вероятность выпадения восьми очков равна .
Стрелок попадает в цель с вероятностью
. Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.
Если вероятность попадания равна — следовательно, вероятность промаха
. Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна
. А вероятность четырех попаданий подряд равна
.
Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей
ПОДРОБНЕЕ
Вероятность: логика перебора.
В кармане у Пети было
монеты по
рублей и
монеты по
рублей. Петя не глядя переложил какие-то
монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?
Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами
— а затем посчитать, сколькими способами можно выбрать три элемента из набора
.
Однако есть более простое решение:
Кодируем монеты числами: ,
(это пятирублёвые),
(это десятирублёвые). Условие задачи можно теперь сформулировать так:
Есть шесть фишек с номерами от до
. Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами
и
не оказались вместе?
Давайте запишем, что у нас в первом кармане.
Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях
и
— это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:
…
А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:
.
Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:
.
Всего возможных исходов.
У нас есть условие — фишки с номерами и
не должны оказаться вместе. Это значит, например, что комбинация
нам не подходит — она означает, что фишки
и
обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только
, либо только
. Вот они:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего благоприятных исходов.
Тогда искомая вероятность равна .
Ответ: .
Сумма событий, произведение событий и их комбинации
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.
– вероятность того, что он сломается на второй год,
– вероятность того, что он прослужит больше двух лет.
Очевидно,
Тогда
Ответ: 0,06.
События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.
Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.
В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.
Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.
Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью
На каждой развилке вероятность свернуть в ту или другую сторону равна
а поскольку развилок пять, вероятность выбраться через выход А равна
то есть 0,03125.
События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.
В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.
Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.
(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?
Вероятность для первого грузовика благополучно одолеть горку Для второго
Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.
Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.
Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна
.
Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.
Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.
Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:
Вероятность того, что яйцо из второго хозяйства и высшей категории, равна
Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.
Мы получили уравнение:
Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).
Пациенту делают анализ. Покажем на схеме все возможные исходы:
Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.
Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.
Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна
). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна
Ответ: 0,0545.
Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна
Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна
В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.
Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.
Еще задачи ЕГЭ по теме «Теория вероятностей».
Смотрите также: парадокс Монти Холла.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3. Теория вероятностей на ЕГЭ по математике.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Раздел «Элементы комбинаторики, статистики и теории вероятностей» в материалах открытого банка заданий ФИПИ по математике ЕГЭ профильного уровня содержит 403 задачи на 41 странице. В статье выделены несколько типов задач по различным темам курса теории вероятностей и предложены способы их решения. Каждый тип задач сопровождают минимально необходимые теоретические сведения. Формулировки задач скопированы с сайта ФИПИ.
1. Задачи на применение классической формулы вероятности события
Вероятностью события А называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу: .
Задача 1.1. В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Решение. Число благоприятных исходов – это и есть число канадских спортсменок. Их 70-(25+17) =28. Общее число исходов – 70, это количество спортсменок, участвующих в чемпионате. Итак, искомая вероятность равна 28/70 = 0,4.
Ответ: 0,4.
Замечание: решительно всё равно, какой по счёту, первой, как в условии задачи, или второй, третьей, …, семидесятой будет выступать канадская спортсменка. Искомая вероятность зависит только от количества канадских гимнасток и общего количества участниц.
Задача 1.2. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 теннисистов, среди которых 7 спортсменов из России, в том числе Анатолий Москвин. Найдите вероятность того, что в первом туре Анатолий Москвин будет играть с каким-либо теннисистом из России.
Решение. Для выбранного уже по условию задачи россиянина Анатолия Москвина благоприятных исходов (его партнёр — российский теннисист) остаётся всего 6. Уменьшается на единицу и общее число всех равновозможных исходов – число спортсменов, готовых сражаться с Москвиным, их – 75. Значит, искомая вероятность равна 6/75 = 0,008.
Ответ: 0,08.
Задача 1.3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
Решение. Перечислим все возможные исходы (их 4) при двух бросаниях монеты:
| N исходов |
Первое бросание |
Второе бросание |
|
|
Решка |
Решка |
|
|
Орёл |
Орёл |
|
|
Орёл |
Решка |
|
|
Решка |
Орёл |
Видно из таблицы, что интересующему нас событию (ровно одному появлению решки) благоприятствуют исходы с номерами 3 и 4. Их два, а возможных исходов в нашем случае – 4. Стало быть, искомая вероятность равна 2/4 = 0,5.
Ответ: 0,5.
Задача 1.4. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет оба раза.
Решение. Благоприятному событию (А) — орёл выпадет оба раза благоприятствует один исход – номер 2 (см. задачу 1.3). Таким образом, Р(А) = 1/4 = 0,25.
Ответ: 0,25.
Задача 1.5. На олимпиаде по русскому языку 350 участников разместили в трёх аудиториях. В первых двух удалось разместить по 140 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение. Найдём количество человек, писавших олимпиаду в запасной аудитории: 350-(140+140) =70. Значит, искомая вероятность равна 70/350 =0,2
Ответ: 0,2.
Задача 1.6. В группе туристов 300 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 15 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист В. полетит первым рейсом вертолёта.
Решение. Способ 1. Интересующее нас событие – «турист В. полетит первым рейсом вертолёта» означает, что он попадает в число15 человек, вылетающих первым рейсом, поэтому искомая вероятность есть 15/300 = 0,05.
Способ 2. Всего рейсов 300/15 = 20. Туристу В, согласно условию задачи, подходит только один из них, значит, вероятность определяется отношением 1/20 = 0,05.
Ответ: 0,05.
Задача 1.7. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 3 сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение. Качественных сумок 100, а общее число сумок 100+3=103. Значит, вероятность вычисляется как отношение 100/103 ≈ 0,971 ≈ 0,97.
Ответ: 0,97.
Задача 1.8. В школе 51 пятиклассник, среди них — Саша и Настя. Всех пятиклассников случайным образом делят на три группы, по 17 человек в каждой. Найдите вероятность того, что Саша и Настя окажутся в одной группе.
Решение. Предполагаем, что Саша уже попал в одну из трёх групп, безразлично, какую. Для Насти, таким образом, число мест в Сашиной группе сократилось до 16, т.к. место занято Сашей. Заметим, что на единицу уменьшилось и общее число участников распределения по группам, т.к. из их числа уже исключён Саша. Таким образом, вероятность того, что Саша и Настя окажутся в одной группе, равна 16/50 = 0,32.
Ответ: 0,32.
Задача 1.9. В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение. При бросании двух игральных костей возможны 36 исходов испытания, т.к. любой исход испытания при бросании первой кости (1, 2, 3, 4, 5, 6) может сочетаться с любым из шести исходов (1, 2, 3, 4, 5, 6) при бросании второй кости. Интересующему нас событию — в сумме выпадет 7 очков благоприятны исходы: 1 и 6, 6 и 1, 5 и 2, 2 и 5, 4 и 3, 3 и 4. Их всего – 6. Значит, искомая вероятность 6/36 = 0,1(6) ≈ 0,17.
Ответ: 0,17.
Задача 1.10. В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
Решение. Как и в предыдущей задаче, общее число всех равновозможных исходов – 36. Благоприятными исходами будут: 6 и 3, 3 и 6, 4 и 5, 5 и 4. Их всего четыре. Вычисляем вероятность: 4/36 = 0,(1) ≈0,11.
Ответ: 0,11.
Задача 1.11. В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 11 очков. Результат округлите до сотых.
Решение. Всех равновозможных исходов – 36. Благоприятные: 5 и 6, 6 и 5. Их два, и поэтому вероятность равна 2/36 = 1/18 ≈ 0,06.
Ответ: 0,06.
Задача 1.12. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнёт игру с мячом не более одного раза.
Решение. Составим таблицу, в которой символ «+» обозначит тот факт, что команда Сапфир начинает игру, а символ будет означать, что игру начинает другая команда (соперник Сапфира):
| № исходов |
I команда |
II команда |
III команда |
|
1 |
+ |
+ |
+ |
|
2 |
+ |
+ |
— |
|
3 |
+ |
— |
+ |
|
4 |
— |
+ |
+ |
|
5 |
— |
— |
+ |
|
6 |
— |
+ |
— |
|
7 |
+ |
— |
— |
|
8 |
— |
— |
— |
Очевидно, что интересующему нас событию А — в этих матчах команда «Сапфир» начнёт игру с мячом не более одного раза, благоприятствуют исходы с номерами 5, 6, 7, 8. Всего исходов – 8, значит, вероятность равна 4/8 = 0,5.
Ответ: 0,5.
Задача 1.13. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом все три раза.
Решение. Таблица исходов приведена в предыдущей задаче. Событию А — в этих матчах команда «Биолог» начнёт игру с мячом все три раза, благоприятствует исход с номером 1 (он – единственный). Таким образом, искомая вероятность вычисляется как отношение 1/8 = 0,125.
Ответ: 0,125.
Задача 1.14. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
Решение. При рассмотрении подобных задач на геометрическую вероятность полезно иметь ввиду, что один час на двенадцатичасовом циферблате занимает сектор 360o/12 = 30o. От 7 до 1 проходит 6 часов, часовая стрелка преодолевает 30o × 6 = 180o, таким образом, искомая вероятность вычисляется как 180/360 = 0,5.
С другой стороны, посмотрев на 12-часовой циферблат, можем видеть, что промежуток от 7 часов до 1 часа занимает ровно половину циферблата, значит, вероятность равна 0,5.
Ответ: 0,5.
Задача 1.15. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет все три раза.
Решение. Все возможные исходы (их 
| № исхода |
1-е бросание |
2-е бросание |
3-e бросание |
|
1 |
Орёл |
Орёл |
Орёл |
|
2 |
Орёл |
Решка |
Решка |
|
3 |
Решка |
Орёл |
Решка |
|
4 |
Решка |
Решка |
Орёл |
|
5 |
Орёл |
Орёл |
Решка |
|
6 |
Решка |
Орёл |
Орёл |
|
7 |
Орёл |
Решка |
Орёл |
|
8 |
Решка |
Решка |
Решка |
Благоприятный исход один – последний: Решка-Решка-Решка. Вероятность, согласно классической формуле, равна 1/8 = 0,125.
Ответ: 0,125.
Задача 1.16. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение. Можно составить таблицу и для четырёх бросаний симметричной монеты:
| № исхода |
1-е бросание |
2-е бросание |
3-e бросание |
4-e бросание |
|
1 |
Решка |
Решка |
Решка |
Решка |
|
2 |
Решка |
Решка |
Решка |
Орёл |
|
3 |
Орёл |
Решка |
Решка |
Решка |
|
4 |
Решка |
Орёл |
Решка |
Решка |
|
5 |
Решка |
Решка |
Орёл |
Решка |
|
6 |
Решка |
Решка |
Орёл |
Орёл |
|
7 |
Орёл |
Орёл |
Решка |
Решка |
|
8 |
Орёл |
Решка |
Решка |
Орёл |
|
9 |
Решка |
Орёл |
Орёл |
Решка |
|
10 |
Решка |
Орёл |
Решка |
Орёл |
|
11 |
Орёл |
Решка |
Орёл |
Решка |
|
12 |
Решка |
Орёл |
Орёл |
Орёл |
|
13 |
Орёл |
Решка |
Орёл |
Орёл |
|
14 |
Орёл |
Орёл |
Решка |
Орёл |
|
15 |
Орёл |
Орёл |
Орёл |
Решка |
|
16 |
Орёл |
Орёл |
Орёл |
Орёл |
Число исходов равно 16. Благоприятные исходы в таблице имеют номера: 6,7,8,9,10,11. Их всего 6. Значит, вероятность равна 6/16 = 3/8 = 0.375.
Если взять на себя труд и выучить теорему Я.Бернулли, то составления таблицы можно избежать.
Теорема: Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Pn(k) того, что в серии n однородных независимых испытаний событие А наступит ровно k раз, равна:
(1).
Здесь – число сочетаний из n элементов по k в каждом, q – вероятность события, противоположного событию А.
В условиях нашей задачи p = 1/2, q = 1 — 1/2 = 1/2,
Подставляем в формулу (1) и получаем :
Ответ: 0,375.
2. Задачи на нахождение вероятности противоположного события
3. Задачи на применение теоремы сложения вероятностей для несовместных событий
4. Задачи на применение теоремы умножения вероятностей независимых событий
ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 2.
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 2 проверяет умение использовать элементы теории вероятностей при решении прикладных задач. Для его выполнения понадобится производить действия с дробями и совершать простые вычисления. Задание представляет собой текстовую задачу, которая решается с помощью базовых арифметических операций. В ответе необходимо указать целое или дробное число, записанное в виде конечной десятичной дроби.
План выполнения:
- Внимательно прочитайте задачу.
- Выявите число всех элементарных событий и число благоприятствующих событий, не пропустив ни одного из всех возможных исходов и не включая ни одного лишнего.
- При решении задачи на классическое определение вероятности установите, зависимы (совместны) или независимы (несовместны) элементарные события.
- Выполните на черновике необходимые вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на классическое
определение вероятности
Задача № 2 (1). В коробке лежит 40 шаров: 20 чёрных, 4 жёлтых и 16 зелёных. Наугад из коробки достают один шар. Найдите вероятность того, что этот шар будет жёлтым.
Решение:
Ответ: 0,1.
Задача № 2 (2). Участников шахматного турнира разбивают на пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 спортсменов из России, в том числе Пётр Орлов. Найдите вероятность того, что Пётр Орлов будет играть с шахматистом из России.
Решение:
Ответ: 0,4.
Задача № 2 (3). У Дениса в копилке лежит 6 рублёвых, 3 двухрублёвых, 2 пятирублёвых и 4 десятирублёвых монеты. Денис наугад достал из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 60 рублей.
Решение:
Ответ: 0,4.
Задачи на использование теорем
о вероятностях событий
Задача № 2 (4). Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Ответ: 0,96.
Задача № 2 (5). При проверке на вирусное заболевание делают анализ крови. Если анализ выявляет вирус, то результат является положительным. У больных анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на заболевание, действительно больны. Найдите вероятность того, что результат анализа у пациента будет положительным. Ответ округлите до сотых.
Решение:
Ответ: 0,05.
Задача № 2 (6). На экзамене по истории ученик отвечает на один вопрос из списка. Вероятность того, что это вопрос по теме «Крепостное право», равна 0,2. Вероятность того, что это вопрос по теме «Февральская революция», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене ученику достанется вопрос по одной из этих двух тем.
Решение:
Ответ: 0,35.
Тренировочные задания с самопроверкой
№ 2.1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.
Открыть ОТВЕТ
№ 2.2. В некотором городе на 6000 появившихся на свет младенцев приходится 3360 девочек. Найдите частоту рождения мальчиков в этом городе.
Открыть ОТВЕТ
№ 2.3. Вероятность того, что на тесте по математике ученица Настя верно решит не менее 12 задач, равна 0,84. Вероятность того, что Настя решит больше 11 задач, равна 0,96. Найдите вероятность того, что Настя решит ровно 12 задач.
Открыть ОТВЕТ
№ 2.4. Склад освещается двумя фонарями с лампами. Вероятность перегорания лампы одного фонаря в течение одного месяца равна 0,4. Найдите вероятность того, что в течение месяца хотя бы одна лампа не перегорит.
Открыть ОТВЕТ
№ 2.5. Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
17 522