ЕГЭ по физике состоит из 31 задания в двух частях.
Первая часть содержит 23 задания с кратким ответом:
- 13 заданий с кратким ответом в виде числа, слова или двух чисел
- 10 заданий на установление соответствия и множественный выбор
Вторая часть состоит из восьми заданий — решение задач. Для трех задач необходимо привести краткий ответ (задания с 24 по 26) и для пяти оставшихся заданий ответ должен быть развернутый (с решением).
В ЕГЭ по физике нас будут ждать следующие темы:
- Механика (кинематика, динамика, статика, законы сохранения в механике, механические колебания и волны)
- Молекулярная физика (молекулярно-кинетическая теория, термодинамика)
- Электродинамика и основы СТО (электрическое поле, постоянный ток, магнитное поле, электромагнитная индукция, электромагнитные колебания и волны, оптика, основы СТО)
- Квантовая физика (корпускулярно-волновой дуализм, физика атома, физика атомного ядра)
Общее количество заданий в экзаменационной работе по каждому из разделов приблизительно пропорционально его содержательному наполнению и учебному времени, отводимому на изучение данного раздела в школьном курсе физики.
| Части работы | Количество заданий | Максимальный первичный бал | Тип заданий |
| 1 часть | 24 | 34 | Краткий ответ |
| 2 часть | 8 | 18 | Развернутый ответ |
| Итого | 32 | 52 |
Время
На выполнение работы отводится 235 минут. Рекомендуемое время на выполнение заданий различных частей работы составляет:
- для каждого задания с кратким ответом 3–5 минут
- для каждого задания с развернутым ответом 15–25 минут
ЕГЭ по физике
Эксперты предметной комиссии записали для выпускников видеоролик с советами по подготовке к экзамену.
Вебинар ФИПИ для учителей физики
Результаты анализа выполнения заданий ЕГЭ 2022 года по физике и особенности КИМ ЕГЭ 2023 года.
Разбор ЕГЭ 2022 по физике
Как это было? Обзор прошедшего ЕГЭ по физике 6 июня.
Разбор досрочного варианта по физике
Вариант был опубликован ФИПИ 28 апреля.
Два способа решения задачи по механике
Решение задания №25 двумя способами: через второй закон Ньютона и через закон сохранения механической энергии.
Сила трения
На вебинаре поговорим о силе трения, её природе, способах вычисления, интересных особенностях и новых заданиях в ЕГЭ.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
ЕГЭ по физике с решением
Равномерное прямолинейное движение материальной точки — это движение, при котором тело за равные промежутки времени совершает одинаковые перемещения. Траектория при таком движении — прямая. Скорость тела постоянна (displaystyle vec {v}=const.)
Уравнение координаты материальной точки в проекциях на ось при равномерном движении:
[x=x_0+v_text{0x}t]
Перемещение:
[S_x=v_text{0x}t]
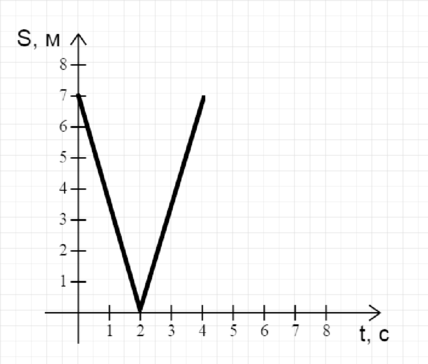
Из двух концов комнаты навстречу друг другу с постоянной скоростью движутся МО и Рыжий Боб. На графике показана зависимость расстояния между ними от времени. Скорость МО равна 3,14 м/с. С какой скоростью движется Рыжий Боб? (Ответ дайте в м/с)
По графику определяем, что расстояние между МО и Рыжим Бобом в начальный момент времени (S=7) м, а время, спустя которое они встретятся, (t=2) c. Перейдем в подвижную систему отсчета относительно МО. Тогда по закону сложения скоростей Рыжий Боб будет двигаться к нему со скоростью: [upsilon=upsilon_1+upsilon_2,] где (upsilon_1) и (upsilon_2) — скорости МО и Рыжего Боба соответственно (относительно неподвижной системы отсчета).
По закону равномерного прямолинейного движения: [S=upsilon t] Подставим сюда предыдущую формулу, и получим: [S=(upsilon_1+upsilon_2)t] Осталось выразить отсюда скорость Рыжего Боба: [upsilon_2=dfrac{S}{t}-upsilon_1=dfrac{7 text{ м}}{2~c}-3{,}14 text{ м/c} = 0{,}36 text{ м/c} .]
Ответ: 0,36
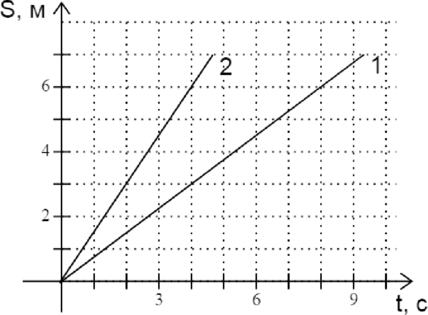
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела (upsilon_2) больше скорости первого тела (upsilon_1).
Т.к. пройденные пути тел линейно увеличиваются, тела движутся равномерно и прямолинейно.
По графику определяем, что первое тело за время (t_1=4) с проходит путь (S_1=3) м, а второе тело за время (t_2=2~c) проходит путь (S_2=3) м. По закону равномерного прямолинейного движения: [S_1=upsilon_1t_1
quad
S_2=upsilon_2t_2] Отсюда выразим (upsilon_1) и (upsilon_2): [upsilon_1=dfrac{S_1}{t_1}; quad
upsilon_2=dfrac{S_2}{t_2}.] Найдем (dfrac{upsilon_2}{upsilon_1}): [dfrac{upsilon_2}{upsilon_1}=dfrac{dfrac{S_2}{t_2}}{dfrac{S_1}{t_1}}=dfrac{dfrac{3 text{ м}}{2~c}}{dfrac{3 text{ м}}{4~c}}=2]
Ответ: 2
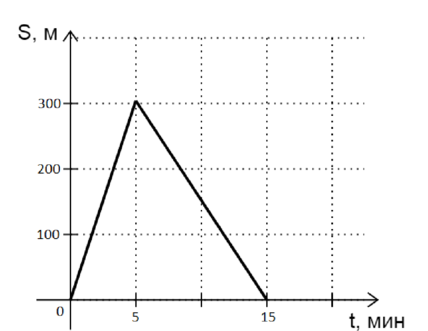
Дима каждый день ходит в школу. На рисунке представлен график движения Димы из дома в школу и обратно. Дом находится в точке (S=0), а школа — в точке (S=300) м. Чему равен модуль скорости Димы на пути из школы домой? (Ответ дайте в м/с)
Рассмотрим график: весь путь Дима двигался прямолинейно и равномерно (но в точке (S=300) м изменил свою скорость). Сначала он двигался из дома в школу со скоростью (upsilon_1) в течение времени (t_1=5) мин, после чего возвращался из школы домой cо скоростью (upsilon_2) в течение времени (t_2): [t_2=15text{ мин}-5text{ мин}=10text{ мин}=10cdot60text{ c}=600~text{ с}.] Чтобы найти (upsilon_2), нам необходимо рассмотреть участок движения Димы по пути из школы домой ((S_2)).
По закону равномерного прямолинейного движения: [S_2=upsilon_2t_2,] где (S_2=0text{ м}-300text{ м}=-300text{ м}).
Отсюда выражаем (upsilon_2): [upsilon_2=dfrac{S_2}{t_2}=dfrac{-300~text{м}}{600~text{c}}=-0,5~text{м/с}] Значит, (|upsilon_2|=|-0,5|text{ м/с}=0,5text{ м/с })
Ответ: 0,5
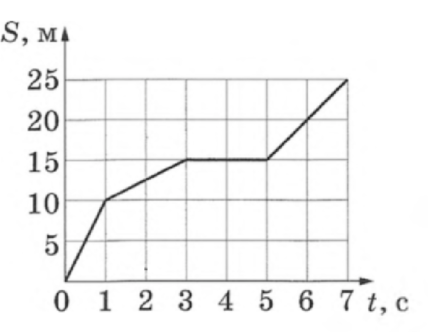
На рисунке представлен график зависимости пути (S), пройденного материальной точкой, от времени (t). Определите скорость (upsilon) точки на интервале времени от 5 с до 7 с. (Ответ дайте в м/с)
Т.к. пройденный путь материальной точки на интервале времени от 5 c до 7 c линейно увеличивается, материальная точка на этом интервале движется равномерно и прямолинейно. По закону равномерного прямолинейного движения:
[Delta S=upsilonDelta t,] где (Delta S=25 text{ м}-15text{ м}=10text{ м}), а (Delta t=7text{ c}-5text{ c}=2text{ c}). Выразим (upsilon): [upsilon=dfrac{Delta S}{Delta t}=dfrac{10text{ м}}{2text{ c}}=5text{ м/c}]
Ответ: 5
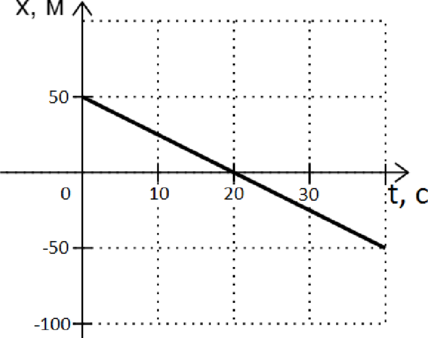
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении по оси Ox. Чему равна (upsilon_x) проекция скорости тела на ось Ох? (Ответ дайте в м/с)
Т.к. пройденный путь тела линейно уменьшается, тело движется равномерно и прямолинейно, и скорость тела постоянна: (upsilon_x=const). По закону прямолинейного равномерного движения тела: [Delta S=upsilon_xDelta t,] где (Delta S=-50text{ м}-50text{ м}=-100) — перемещение тела, а (Delta t=40 c) — время перемещения.
Отсюда выразим (upsilon_x): [upsilon_x=dfrac{Delta S}{Delta t}=dfrac{-100text{ м}}{40text{ c}}=-2,5~dfrac{text{м}}{text{c}}]
Ответ: -2,5
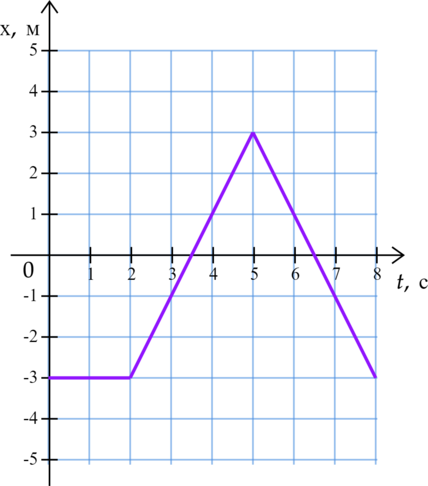
На рисунке приведен график зависимости координаты тела от времени при прямолинейном движении по оси (x). Какова проекция (upsilon_x) скорости тела в промежутке от 5 (c) до 8 (c)? (Ответ дайте в м/с)
Найдем изменение координаты тела в промежутке от 5 (c) до 8 (c). Для этого из конечной координаты вычтем начальную: [Delta x=x_text{к}-x_text{н}]
Подставим исходные данные: [Delta x=(-3)text{ м}-3text{ м}=-6text{ м}]
Найдем изменение времени в промежутке от 5 (c) до 8 (c): [Delta t=t_text{к}-t_text{н}]
Подставим исходные данные: [Delta t=8text{ с}-5text{ с}=3text{ c}]
Найдем проекцию скорости тела:
[upsilon_x=frac{Delta x}{Delta t}]
Подставим исходные данные: [upsilon_x=frac{-6text{ м}}{3text{ c}}=-2text{ м/c}]
Ответ: -2
Движение двух велосипедистов задано уравнениями (x_1=3t) (м) и (x_2=12-t) (м). Велосипедисты двигаются вдоль одной прямой. Найдите координату (x) места встречи велосипедистов. (Ответ дайте в метрах)
1 способ:
Велосипедисты встретятся, если совпадут их координаты, отсюда: [x_1=x_2]
Подставим уравнения: [3t=12-t] [4t=12]
Отсюда время, в которое встретятся велосипедисты: [t=3text{ c}]
Найдем координату (x) места встречи велосипедистов, для этого подставим время (t) в оба уравнения: [x_1=3cdot3=9text{ м}] [x_2=12-3=9text{ м}]
2 способ:
Изобразим движение велосипедистов: 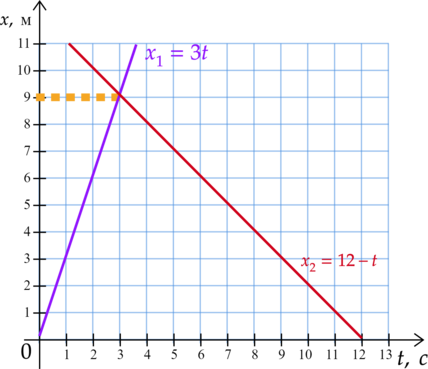
Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Доступность
Смотреть видеоурок ЕГЭ по математике профильного уровня можно в любое время и в любом месте.
Достаточно иметь какое-либо устройство с выходом в Интернет:
- Персональный компьютер
- Ноутбук
- Планшет
- Смартфон
Удобство
Видеоуроки для подготовки к ЕГЭ по математике позволяют максимально рационально использовать свободное от учебы время. Вам не придется тратить драгоценные минуты на поездки к репетитору или в какие-либо обучающие центры. Видеоуроки ЕГЭ по математике, посмотреть которые вы можете на образовательном портале «Школково», содержат весь необходимый материал для эффективной подготовки к экзамену. Кроме того, наш ресурс позволяет каждому ученику выстроить коммуникацию со своим преподавателем.
Информативность
Каждый школьник может выбрать именно тот видеоурок ЕГЭ по математике, тема которого соответствует изучаемому или повторяемому им материалу. Таким образом, выпускник может быстрее и легче усвоить новую информацию или восполнить пробелы в знаниях.
При подготовке к экзамену нужно делать упор не на его сдачу как самоцель, а на повышение уровня знаний учащегося. Для этого необходимо изучать теорию, отрабатывать навыки, решая разнообразные варианты профильного ЕГЭ по математике нестандартными способами с развернутыми ответами, следить за динамикой обучения.
А поможет вам во всем этом образовательный проект «Школково».