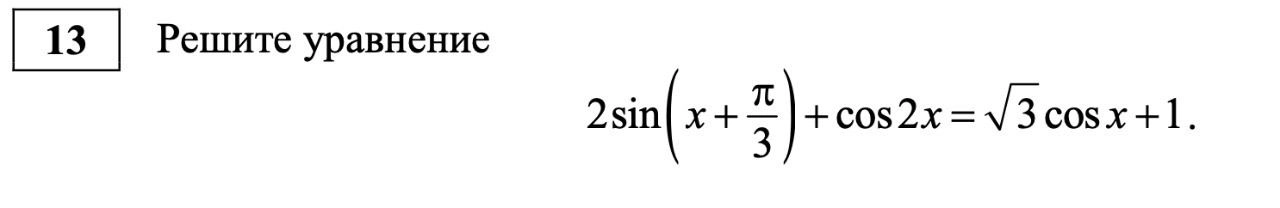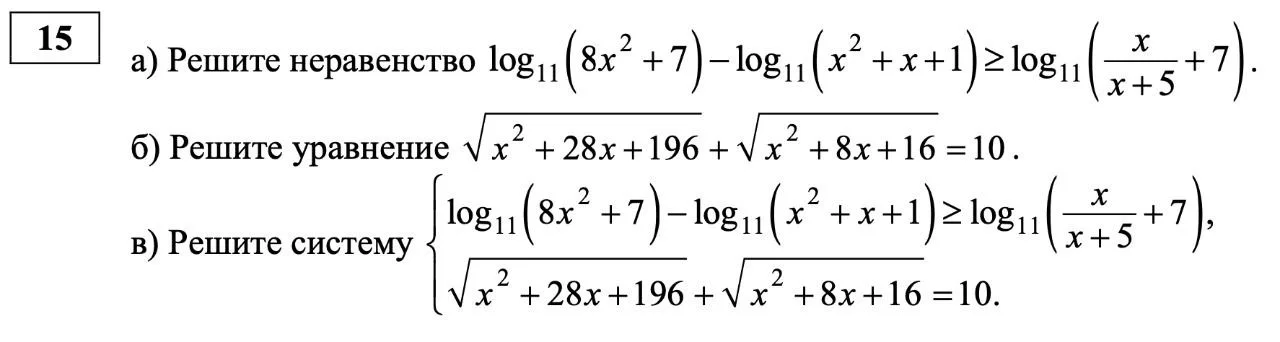5 сентября 2019
В закладки
Обсудить
Жалоба
Средний процент выполнения заданий ЕГЭ по математике
Таблица с результатами выполнения заданий ЕГЭ по математике в 2019 году.
Профильный уровень
|
№ |
Проверяемые требования (умения) |
Уровень сложности задания |
Максимальный балл за выполнение задания | Средний процент выполнения |
| 1 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 95,5 |
| 2 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 95,5 |
| 3 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б | 1 | 93,3 |
| 4 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 95 |
| 5 | Уметь решать уравнения и неравенства |
Б | 1 | 93,6 |
| 6 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б | 1 | 80,6 |
| 7 | Уметь выполнять действия с функциями |
Б | 1 | 61,5 |
| 8 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б | 1 | 66,7 |
| 9 | Уметь выполнять вычисления и преобразования |
П | 1 | 74,8 |
| 10 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
П | 1 | 86,9 |
| 11 | Уметь строить и исследовать простейшие математические модели |
П | 1 | 72,7 |
| 12 | Уметь выполнять действия с функциями |
П | 1 | 60,8 |
| 13 | Уметь решать уравнения и неравенства |
П | 2 | 45,3 |
| 14 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П | 2 | 5,6 |
| 15 | Уметь решать уравнения и неравенства |
П | 2 | 20,8 |
| 16 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П | 3 | 2,7 |
| 17 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
П | 3 | 15,4 |
| 18 | Уметь решать уравнения и неравенства |
В | 4 | 4,2 |
| 19 | Уметь строить и исследовать простейшие математические модели |
В | 4 | 3,2 |
Базовый уровень
| № |
Проверяемые требования |
Уровень сложности задания |
Максимальный балл за выполнение задания | Средний процент выполнения |
| 1 | Уметь выполнять вычисления и преобразования |
Б | 1 | 86,1 |
| 2 | Уметь выполнять вычисления и преобразования |
Б | 1 | 84 |
| 3 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 84,8 |
| 4 | Уметь выполнять вычисления и преобразования |
Б | 1 | 86,9 |
| 5 | Уметь выполнять вычисления и преобразования |
Б | 1 | 83,4 |
| 6 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 82,6 |
| 7 | Уметь решать уравнения и неравенства | Б | 1 | 69,9 |
| 8 | Уметь строить и исследовать простейшие математические модели | Б | 1 | 76,2 |
| 9 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 95,4 |
| 10 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 71,8 |
| 11 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни |
Б | 1 | 95,5 |
| 12 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 90,3 |
| 13 | Уметь выполнять действия с геометрическими фигурами | Б | 1 | 38,4 |
| 14 | Уметь выполнять действия с функциями | Б | 1 | 62,4 |
| 15 | Уметь выполнять действия с геометрическими фигурами | Б | 1 | 53,9 |
| 16 | Уметь выполнять действия с геометрическими фигурами | Б | 1 | 53,5 |
| 17 | Уметь решать уравнения и неравенства | Б | 1 | 69,2 |
| 18 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 84,8 |
| 19 | Уметь выполнять вычисления и преобразования |
Б | 1 | 64,2 |
| 20 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 27,8 |
Анализ выполнения заданий
ЕГЭ по математике (профильный уровни) в 2020 году (учитель Петрашова В.Н.)
В ЕГЭ по математике (профильный уровень) приняли участие 11 обучающихся.
Каждый вариант КИМ состоял из двух типов заданий:
задания с кратким ответом в виде целого числа или конечной десятичной дроби (задания №№ 1-12). В работе задания с кратким ответом по уровню сложности распределены на базовый (№№ 1-8) и повышенный (№№ 9-12);
задания с развернутым ответом с полной записью решения с обоснованием выполненных действий (задания №№ 13–19).
Минимальный порог для поступления в вузы и получения аттестата составляет 6 первичных баллов или 27баллов по стобальной системе.
Не перешел порог А. (23б)
Наилучший результат К. (80б)
Средний первичный балл по итогам ЕГЭ составил 11баллов.
Средний балл по итогам ЕГЭ составил 53 балла.
Средний балл по итогам ЕГЭ по городу составил 59,18 балла.
Средний процент выполнения заданий первой части составил 78%.
Три ученика: А., К. и Е. выполнили задания первой части на 100%; Е. на 92%; Т. на 83%.
100% выполнение заданий № 2,3,4,5.
91% выполнение заданий № 1.
82% выполнение заданий № 8,9.
73% выполнение заданий № 10,11.
«Западающими» заданиями оказались № 6,7,12.
Выполнение заданий с кратким ответом является показателем готовности обучающихся к ЕГЭ, поскольку правильное выполнение только всех двенадцати заданий с кратким ответом при переводе в тестовые баллы позволяет набрать участнику 62 балла, что является хорошим шансом поступления на бюджет в региональные вузы.
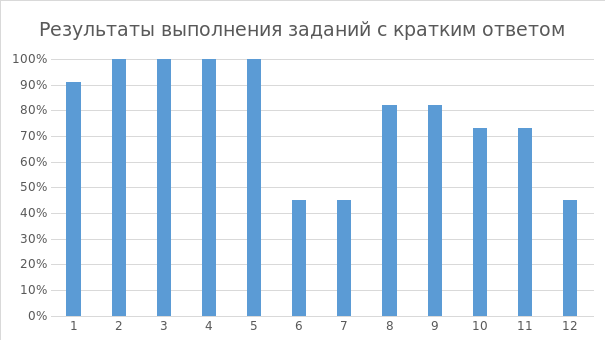
Содержательный элемент считается усвоенным на достаточном уровне обучающимися, если процент выполнения заданий базового уровня сложности составляет 60 и более процентов. Показатели успешности продемонстрированы при решении заданий базового уровня № 1 (простейшая текстовая задача), №2 (чтение диаграмм), №3 (решение задач на квадратной решетке), №4 (задача на отыскание вероятности события), №5 (решение простейших уравнений), №8 стереометрические задачи), №9 (вычисления и преобразования с числами, корнями, тригонометрическими, степенями, логарифмами), №10 ( умения использовать приобретенные знания в повседневной жизни), №11 (применения уравнений и неравенств в математических моделях), что свидетельствует о сформированности у участников ЕГЭ базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Недостаточные результаты выполнения заданий с кратким ответом наблюдались в заданиях базового уровня сложности №6 (планиметрическая задача), № 7 (применение производной к исследованию функций, материал 10 класса, я обучала этих ребят лишь в 11 классе) и повышенного уровня сложности № 12 (применение производной к исследованию функций на монотонность, опять же материал 10 класса).
Сравнительный анализ результативности выполнения заданий первой части
|
Номер |
Проверяемые элементы содержания / |
Результат |
Результат |
|
|
выполнения, |
выполнения, |
|||
|
задания |
умения |
|||
|
2019 год(14уч.) |
2020 год(11 уч.) |
|||
|
1 |
Целые и рациональные числа, проценты, |
100% |
91% |
|
|
применение математических методов для |
||||
|
решения содержательных задач из |
||||
|
различных областей науки и практики. |
||||
|
Интерпретация результата, учёт реальных |
||||
|
ограничений / Уметь использовать |
||||
|
приобретённые знания и умения в |
||||
|
практической деятельности и повседневной |
||||
|
жизни |
||||
|
Графическое представление данных / Уметь |
||||
|
использовать приобретённые знания и |
||||
|
умения в практической деятельности и |
||||
|
2 |
повседневной жизни: описание с помощью |
100% |
100% |
|
|
функций различных реальных зависимостей |
||||
|
между величинами и интерпретация их |
||||
|
графиков; извлечение информации, |
||||
|
представленной на графиках |
||||
|
3 |
Площадь плоских фигур / Уметь выполнять |
100% |
100% |
|
|
действия с геометрическими фигурами |
||||
|
4 |
Вероятности событий / Уметь вычислять в |
100% |
100% |
|
|
простейших случаях вероятности событий |
||||
|
5 |
Различные уравнения /Уметь решать |
100% |
100% |
|
|
уравнения |
||||
|
6 |
Вписанные углы / Уметь выполнять |
86% |
45% |
|
|
действия с геометрическими фигурами |
||||
|
Применение производной к исследованию |
||||
|
7 |
функций / Уметь выполнять действия с |
50% |
45% |
|
|
функциями |
||||
|
Уметь решать простейшие |
||||
|
8 |
стереометрические задачи на нахождение |
93% |
82% |
|
|
геометрических величин |
||||
|
Числа, корни и степени, тригонометрия, |
||||
|
9 |
логарифмы / Уметь выполнять вычисления |
64% |
82% |
|
|
и преобразования |
||||
|
Уравнения и неравенства / Уметь |
||||
|
10 |
использовать приобретённые знания и |
93% |
73% |
|
|
умения в практической деятельности и |
||||
|
повседневной жизни |
||||
|
Уравнения и неравенства /Уметь строить и |
||||
|
11 |
исследовать простейшие математические |
93% |
73% |
|
|
модели |
||||
|
Производные суммы, разности, основных |
||||
|
элементарных функций / Уметь исследовать |
||||
|
12 |
в простейших случаях функции на |
64% |
45% |
|
|
монотонность, находить наибольшее и |
||||
|
наименьшее значения функции, вычислять |
||||
|
производные элементарных функций. |
В сравнении с результатами ЕГЭ 2019 года произошло снижение показателей по номерам 6 (планиметрическая задача) и 12 (применение производной к исследованию функций на монотонность).
Количество баллов, выставленных за выполнение заданий 13–19, зависело от полноты решения и правильности ответа. Общие требования к выполнению заданий с развёрнутым ответом: решение должно было быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могли быть разными. За решение, в котором обоснованно получен правильный ответ, выставлялось максимальное количество баллов.
Правильный ответ при отсутствии текста решения оценивался в 0 баллов. Эксперты проверяли только математическое содержание представленного решения, а особенности записи не учитывались.
При выполнении задания могли использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.
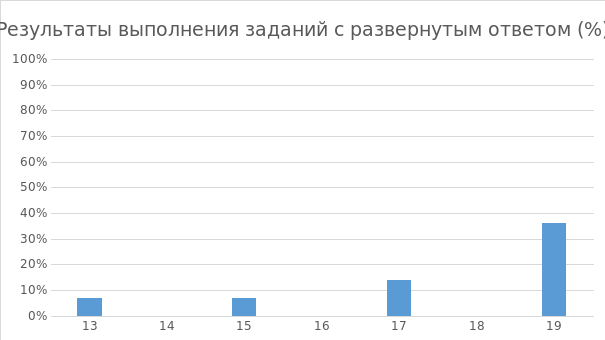
Соответствие доли участников и набранных баллов, полученных за
выполнение заданий с развернутым ответом
|
Доля обучающихся, набравших |
||||
|
№ задания |
соответствующие баллы |
|||
|
0 |
1 |
2 |
||
|
13. |
Тригонометрическое уравнение с отбором |
|||
|
корней |
92% |
8% |
0% |
|
|
14. |
Стереометрическая задача |
100% |
0% |
0% |
|
15. |
Показательное неравенство |
92% |
0% |
8% |
|
Доля обучающихся, набравших |
||||||||||||||
|
№ задания |
соответствующие баллы |
|||||||||||||
|
0 |
1 |
2 |
3 |
|||||||||||
|
16. |
Планиметрическая задача |
100% |
0% |
0% |
0% |
|||||||||
|
17. |
Задача с экономическим содержанием |
84% |
0% |
8% |
8% |
|||||||||
|
Доля обучающихся, набравших соответствующие |
||||||||||||||
|
№ задания |
баллы |
|||||||||||||
|
0 |
1 |
2 |
3 |
4 |
||||||||||
|
18. |
Задача с параметром |
100% |
0% |
0% |
0% |
0% |
||||||||
|
19. |
Задача на решение в целых |
|||||||||||||
|
числах |
60% |
24% |
16% |
0% |
0% |
Результаты заданий с развернутым ответом свидетельствуют о наличии проблемных зон в подготовке обучающихся:
результаты выполнения № 13 значительно снизились.
Предложения по работе с обучающимися, планирующими выполнение экзаменационной работы на профильном уровне на следующий учебный год:
Своевременное выявление учащихся, имеющих слабую математическую подготовку.
Для своевременной корректировки системы подготовки учащихся к итоговой аттестации необходимо выявить пробелы в знаниях учащихся. С этой целью следует проводить диагностические работы с последующим выстраиванием индивидуальной траектории развития обучающегося.
Параллельно с изучением новых тем в курсе алгебры и начал анализа, стереометрии в XI классах следует предусмотреть возможность повторения слабо усвоенных тем и разделов. На уроках повторения целесообразно проводить регулярный контроль усвоения знаний на базовом уровне в соответствии с открытым банком тестовых заданий.
Необходимо существенно усилить внимание к преподаванию курса геометрии в основной и старшей школе, делая акцент не только на овладение теоретическими фактами курса, но и на формирование умения проводить обоснованные решения геометрических задач и математически грамотно их записывать.
Особое внимание следует обратить на практико-ориентированные задачи, поскольку они являются отличительной чертой новых образовательных стандартов.
-
процессе обучения не нужно злоупотреблять тестовой формой контроля; необходимо, чтобы учащийся предъявлял свои рассуждения как материал для дальнейшего их анализа и обсуждения.
Рекомендации по подготовке учащихся, имеющих слабую математическую подготовку:
Каждый учащийся должен быть ознакомлен с открытым банком тестовых заданий.
Выработать навык записи ответов на задания в бланках ответов.
Сформировать умение пользоваться справочными материалами, входящим в состав КИМ.
Для подготовки к государственной итоговой аттестации учащихся, слабо овладевших математическими компетенциями, следует различными диагностическими процедурами выявить 9–12 заданий экзамена базового уровня, которые учащийся может выполнить, возможно, с ошибками, и в процессе обучения добиться уверенного выполнения.
Отработка безошибочного выполнения несложных преобразований и вычислений (в том числе на умение найти ошибку).
Регулярное выполнение упражнений, развивающих базовые математические компетенции школьников (умение читать и верно понимать условие задачи, решать практические задачи, выполнять арифметические действия, простейшие алгебраические преобразования, действия с основными функциями и т.д.).
Особое внимание уделять арифметическим вычислениям, навыки которых у части выпускников либо частично утрачены, либо недостаточно сформированы.
Усилить наглядность при изучении геометрии, изображение геометрических фигур, формирование конструктивных умений и навыков, применение геометрических знаний для решения практических задач.
Освоение базовых объектов и понятий курса стереометрии (углы в пространстве, многогранники, тела вращения, площадь поверхности, объем и т.д.).
Решение простейших задач с небольшим числом вариантов (с расчетом на практическое применение), где возможно явное описание и анализ ситуации при изучении теории вероятностей и статистики.
Рекомендации по подготовке учащихся, имеющих высокую математическую подготовку:
Больше времени уделять логическим рассуждениям, геометрическим (стереометрическим) конструкциям при решении задач.
Изучать с учащимися материал, который не входит в программу школьного курса.
Необходимо учить школьников очень внимательно знакомиться с условием задания.
Поддержание постоянного интереса к предмету путем предложения для решения нестандартных задач (школьникам, как правило, интересны задачи, для решения которых необходимо придумать какой-либо новый способ или использовать знания, выходящие за рамки школьных учебников) и поощрение интереса к изучению внепрограммного материала.
Индивидуальный подход, корректное выстраивание образовательной траектории развития учащегося (рекомендации литературы для подготовки, дать ссылку в сети Интернет, и т.д.), помощь в самоопределении и развитии личности.
Расписание ЕГЭ−2023
| Дата | ЕГЭ |
|---|---|
| Досрочный этап | |
| 20 марта (пн) | география, литература |
| 23 марта (чт) | русский язык |
| 27 марта (пн) | профильная и базовая математики |
| 30 марта (чт) | иностранные языки (за исключением раздела «Говорение»), биология, физика |
| 3 апреля (пн) | иностранные языки (раздел «Говорение») |
| 6 апреля (чт) | обществознание, информатика и ИКТ |
| 10 апреля (пн) | история, химия |
| Основной этап | |
| 26 мая (пт) | география, литература, химия |
| 29 мая (пн) | русский язык |
| 1 июня (чт) | профильная и базовая математики |
| 5 июня (пн) | история, физика |
| 8 июня (чт) | обществознание |
| 13 июня (вт) | иностранные языки (за исключением раздела «Говорение»), биология |
| 16 июня (пт) | иностранные языки (раздел «Говорение») |
| 17 июня (сб) | иностранные языки (раздел «Говорение») |
| 19 июня (пн) | информатика и ИКТ |
| 20 июня (вт) | информатика и ИКТ |
| 22 июня (чт) | резерв: русский язык |
| 23 июня (пт) | резерв: география, литература, иностранные языки (раздел «Говорение») |
| 26 июня (пн) | резерв: профильная и базовая математики |
| 27 июня (вт) | резерв: иностранные языки (за исключением раздела «Говорение»), биология, информатика и ИКТ |
| 28 июня (ср) | резерв: обществознание, химия |
| 29 июня (чт) | резерв: история, физика |
| 1 июля (сб) | резерв: по всем учебным предметам |
Источник
Средний тестовый балл участников профильного экзамена ЕГЭ 2022 г. повысился в сравнении с предыдущими годами и составил 56,9. Также следует отметить заметный рост доли участников, показавших результат в интервале 61–80, то есть основного контингента IT, инженерных, естественно-научных специальностей вузов. Эта важная группа и обеспечила рост среднего тестового балла в 2022 г.
Более подробные аналитические и методические материалы ЕГЭ 2022 года доступны по ссылке.
ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО МАТЕМАТИКЕ 2023 ГОДА
читать полностью: спецификация.
Заданий базового уровня сложности 6, повышенного — 10, высокого — 2.
Работа рассчитана на 235 минут.
Обозначение уровня сложности задания: Б — базовый, П — повышенный, В — высокий.
|
Проверяемые требования (умения) |
Уровень сложности задания |
Максимальный балл за выполнение задания |
Примерное время выполнения задания (мин.) |
|
| Задание 1. Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
5 |
3 |
| Задание 2. Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
10 |
3 |
| Задание 3. Уметь строить и исследовать простейшие математические модели |
Б |
1 |
5 |
2 |
| Задание 4. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
Б |
1 |
15 |
8 |
| Задание 5. Уметь решать уравнения и неравенства |
Б |
1 |
5 |
2 |
| Задание 6. Уметь выполнять вычисления и преобразования |
Б |
1 |
5 |
3 |
| Задание 7. Уметь выполнять действия с функциями |
Б |
1 |
10 |
4 |
| Задание 8. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
П |
1 |
15 |
6 |
| Задание 9. Уметь строить и исследовать простейшие математические модели |
П |
1 |
15 |
7 |
| Задание 10. Уметь выполнять действия с функциями |
П |
1 |
15 |
8 |
| Задание 11. Уметь выполнять действия с функциями |
П |
1 |
15 |
9 |
| Задание 12. Уметь решать уравнения и неравенства |
П |
2 |
20 |
10 |
| Задание 13. Уметь выполнять действия геометрическими фигурами, координатами и векторами |
П |
3 |
40 |
20 |
| Задание 14. Уметь решать уравнения и неравенства |
П |
2 |
30 |
15 |
| Задание 15. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
П |
2 |
30 |
25 |
| Задание 16. Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П |
3 |
35 |
|
| Задание 17. Уметь решать уравнения и неравенства |
В |
4 |
35 |
|
| Задание 18. Уметь строить и исследовать простейшие математические модели |
В |
4 |
40 |
ОФИЦИАЛЬНАЯ ШКАЛА 2022 ГОДА
Первичный балл
Тестовый балл
Соответствие между минимальными первичными баллами и минимальными тестовыми баллами 2022 года. Распоряжение о внесении изменений в приложение № 2 к распоряжению Федеральной службы по надзору в сфере образования и науки. Перейти.
ПОРОГОВЫЕ БАЛЛЫ
Для получения аттестата: 27 тестовых (5 первичных) баллов. См. распоряжение Рособрнадзора.
Для поступления в вузы, подведомственные Министерству науки и высшей школы: 39 тестовых баллов. См. приказ Миннауки.
Для поступления в вузы, подведомственные Министерству просвещения: 39 тестовых баллов. См. приказ Минпроса.
ЭКЗАМЕНАЦИОННЫЕ БЛАНКИ
Правила заполнения бланков государственной итоговой аттестации. Скачать бланки в высоком качестве можно по ссылке.
ЧТО МОЖНО ВЗЯТЬ С СОБОЙ НА ЭКЗАМЕН
На экзамене по математике разрешается пользоваться линейкой, которая не содержит справочную информацию, для построения чертежей и рисунков. Источник.
Задания базовой части ЕГЭ по математике взяты из открытого банка экзаменационных заданий (http://mathege.ru) и представляют собой модельные задачи, на основе которых путем изменения конкретных числовых данных составляются реальные экзаменационные работы ЕГЭ. Задания повышенного и высокого уровня сложности были специально составлены для портала «РЕШУ ЕГЭ» или предлагались в официальных сборниках для подготовки к экзамену.
Авторы задач для подготовки к ЕГЭ:
И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров,
Р. К. Гордин,
А. В. Малышев,
С. В. Панферов, М. А. Посицельская, С. Е. Посицельский,
М. Я. Пратусевич,
С. Е. Рукшин,
А. В. Семенов, А. Л. Семенов, И. Н. Сергеев,
К. М. Столбов,
В. А. Смирнов,
С. А. Шестаков, Д. Э. Шноль, И. В. Ященко;
материалы сайта http://ege.yandex.ru.
Статистика решаемости стереометрических задач в рамках подготовки учащихся к ЕГЭ
Основной формой проверки знаний в средних учебных заведениях в настоящее время является единый государственный экзамен по математике. В нем представлены задания из различных разделов, в том числе и стереометрические задачи. Анализ представленных в ЕГЭ заданий по стереометрии показывает, что наиболее успешно учащиеся справляются с заданиями базового уровня, уровень сложности которых существенно ниже, чем в профильном. К задачам профильного уровня по стереометрии приступает, и успешно решает небольшой процент учащихся, которые нацелены на максимально высокий балл по ЕГЭ. Данные задачи нацелены на достаточно высокий уровень знаний [2,322].
Стереометрия (от др.-греч. στερεός, «стереос» — «твёрдый, пространственный» и μετρέω — «измеряю») — это раздел геометрии, в котором изучаются свойства фигур в пространстве[1,5]. Стереометрия изучается после курса планиметрии и сопряжена с формированием у школьников пространственных представлений, которые развивают отдельный специальный вид задач, встречающихся только в стереометрии на построении пространственных фигур.
Изучение статистики успешности решаемости стереометрических задач базового и профильного уровня позволяет сделать вывод, что далеко не каждый учащийся может успешно справиться с подобным заданием.
Существует ряд проблем, с которыми учащийся сталкивается при решении задач данной тематики. Основными являются недостаточность геометрических знаний, графической культуры учащихся, отсутствие навыка решения подобных заданий из-за недостаточного количества времени, отводимого на изучение стереометрии. Важную роль в формировании и развитии пространственных представлений играют стереометрические задачи на построение. Специфика задач на построение в пространстве состоит в том, что не существует чертежных инструментов, позволяющих чертить геометрические фигуры непосредственно в пространстве. Пространственные фигуры изображаются плоским рисунком, а значит, такой рисунок во многом является условным: линейные и условные размеры на нем искажаются.
В этой связи, при подготовке к ЕГЭ возникает задача анализа заданий по данной теме за прошлые годы проведения экзаменов, выделение структуры и востребованности типовых заданий данной тематики. Мной был проведен небольшой анализ на основе методических рекомендаций Лысенко и Кулабухова, часто встречающихся заданий их процентное соотношение. Рассматривались задания из профильного уровня по решению стереометрических задач. Из 8 задания наиболее часто встречаются задания на нахождение V и S таких поверхностей, как призмы, конуса, цилиндра. Также представлены менее встречающиеся типы заданий [3,6]. Каждое из заданий было направлено на выявление определенных умений и навыков. Например, в задание 8 проверялось умение выполнять действия с геометрическими фигурами, координатами и векторами – на соотношение нахождения объема конуса и цилиндра с равными радиусами основания и высотами, применение формулы боковой поверхности конуса. Данное задание вызвало трудности у учащихся и успешно справиться с ним смогли около 57 % пишущих. В задание 14 учащиеся столкнулись с проблемой неумения доказывать, непонимание взаимосвязи элементов геометрической конструкции, незнание теоретических фактов, неумение строить чертеж[4,16].
рис.1 Базовый уровень, задание 8
рис.2 Профильный уровень, задание 14
Список используемой литературы:
Лапузина Е. Н. Математика: Геометрия. Элементы комбинаторики. Комплексные числа : учеб. пособие / Е. Н. Лапузина, А. И. Лобода, Е. А. Романова ; Харьковский политехнический ин-т, нац. техн. ун-т. – Харьков: НТУ «ХПИ», 2011. – 216 с.
Лысенко Ф.Ф., Кулабухов С.Ю, ЕГЭ 2016, Математика, 10-11 класс, Проф. Уровень 40 тренировочных тестов, 2015.
Лысенко Ф.Ф., Кулабухова С.Ю. Учебно-методической пособие/под редакцией. — Ростов-на-Дону: Легион, 2016.-352 с — (ЕГЭ).
Ященко И.В.,Семенов А.В., Высоцкий И.Р. Методические рекомендации для учителей/под редакцией.-ФИПИ, 2017- 45 с.
Перспективные модели ЕГЭ уже опубликованы на сайте ФИПИ. Разбираем возможные изменения в ЕГЭ 2022 по математике и рассказываем, чего ожидать от реального экзамена.
ЕГЭ по математике не менялся с 2015 года! На фоне масштабных изменений в других предметах это было необычно. Но с учётом сложности этого предмета и сравнительно невысоких средних баллов из года в год, никого это не удивляло. Преподаватели вздыхали с облегчением, что программу подготовки можно не менять. А ученики радовались, что можно посоветоваться с бывшими 11-классниками, потому что они сдавали то же самое.
Но вот появилась перспективная модель ЕГЭ по математике, а значит ФИПИ начал планировать изменения в экзамене. В этой статье мы обсудим их все.
Сразу хочу отметить, что пока перспективная модель только вынесена на обсуждение. А вот демоверсия экзамена по математике 2022 (то есть более точный вариант) уже вышла, и я сделала ее подробный разбор в этой статье. Спойлер: демоверсия отличается от перспективной модели.
При подготовке к ЕГЭ очень важно учитывать все актуальные изменения экзамена. Ровно за это отвечают в образовательном центре MAXIMUM. Наши преподаватели используют лучшие учебные пособия, в которых отражены последние нововведения ЕГЭ. Мы даем нашим ученикам только полезные знания и лайфхаки, которые гарантированно помогут им сдать экзамен на высокий балл. Записывайтесь к нам на бесплатный открытый урок и узнайте все об успешной подготовке к ЕГЭ.
Количество заданий в перспективной модели ЕГЭ по математике
Первая новость хорошая – количество заданий в ЕГЭ по математике НЕ ИЗМЕНИТСЯ! А хорошая она потому, что на существующие 19 заданий не у всех учеников хватало времени. Поверьте преподавателю, который «вытирал слёзы» ученикам, не успевшим написать 19в или 16б.
Изменения в количестве баллов за ЕГЭ по математике
Здесь тоже сильных изменений не будет. Добавится 1 первичный балл за счёт изменений в № 15, но об этом поговорим подробнее чуть позже.
В итоге общий балл будет поднят с 32 до 33.
Общие изменения в перспективной модели ЕГЭ по математике
Самые значительные изменения коснулись части с кратким ответом. В ней мы увидим и исключение заданий, и совершенно новые форматы, а также очень много перестановок. Однако она, как и прежде, будет приносить ученикам 12 первичных баллов.
Что касается части с развёрнутым ответом, то изменения там будут самые незначительные. Содержательно могут изменить только 2 задания, и как раз одно из них и принесёт дополнительный балл. Остальные задания не изменят.
Что убрали из краткой части в перспективной модели ЕГЭ по математике
Как я уже сказала, больше всего изменений планируется в части с кратким ответом. Во-первых, теперь все первые 12 заданий будут называться «Часть 1».
Раньше «Часть 1» включала в себя только первые 8 заданий. Номера 9-12 относились к «Части 2», но записывались в бланк с кратким ответом.
Во-вторых, именно в этой части экзамена мы можем потерять задания. В перспективной модели ЕГЭ по математике нет:
№ 1 – простейшей текстовой задачи
Тип заданий, исключенный из перспективной модели ЕГЭ по математике 2022
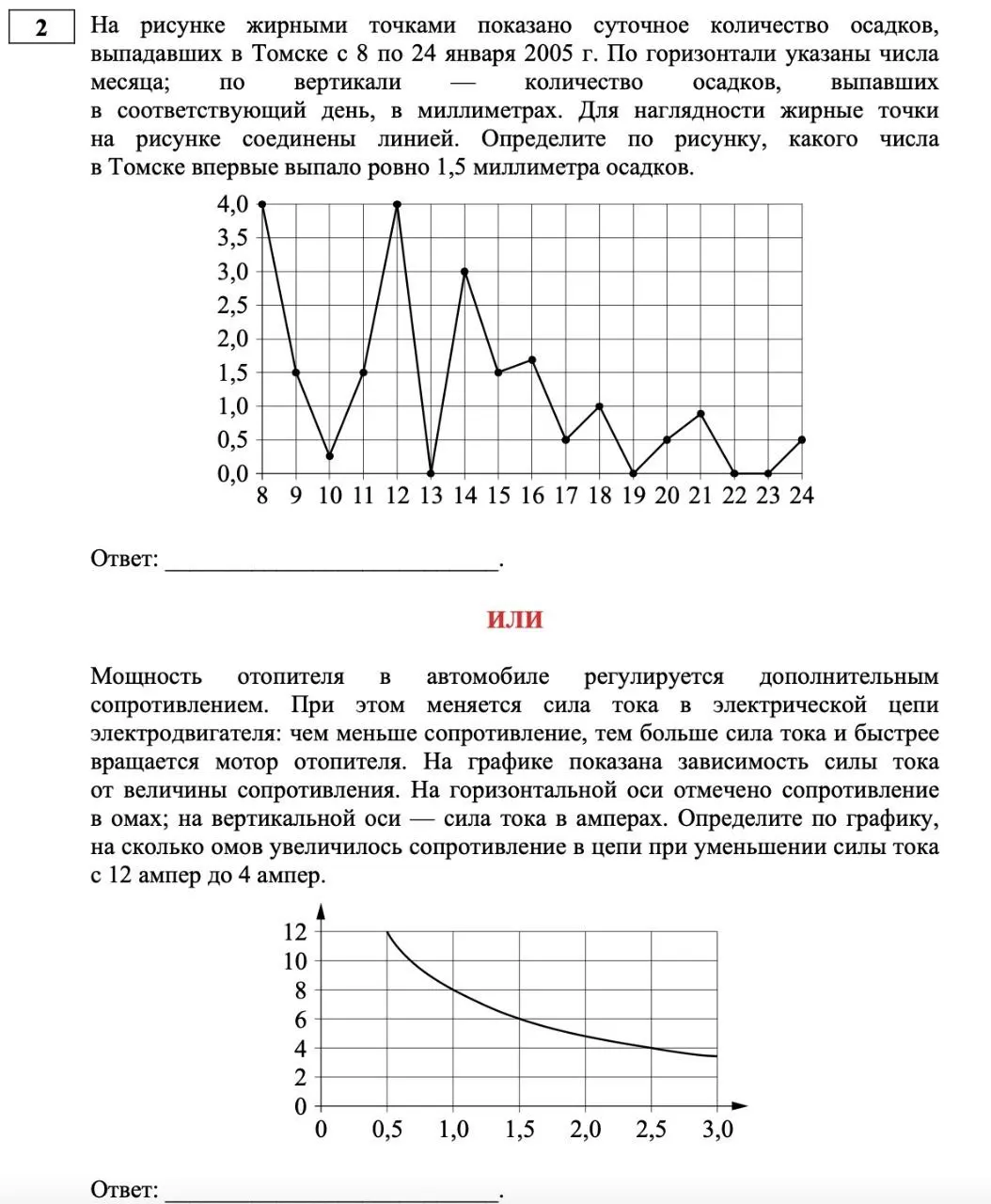
№ 2 – задачи на анализ графиков и диаграмм
Тип задач, которых нет в перспективной модели ЕГЭ по математике 2022
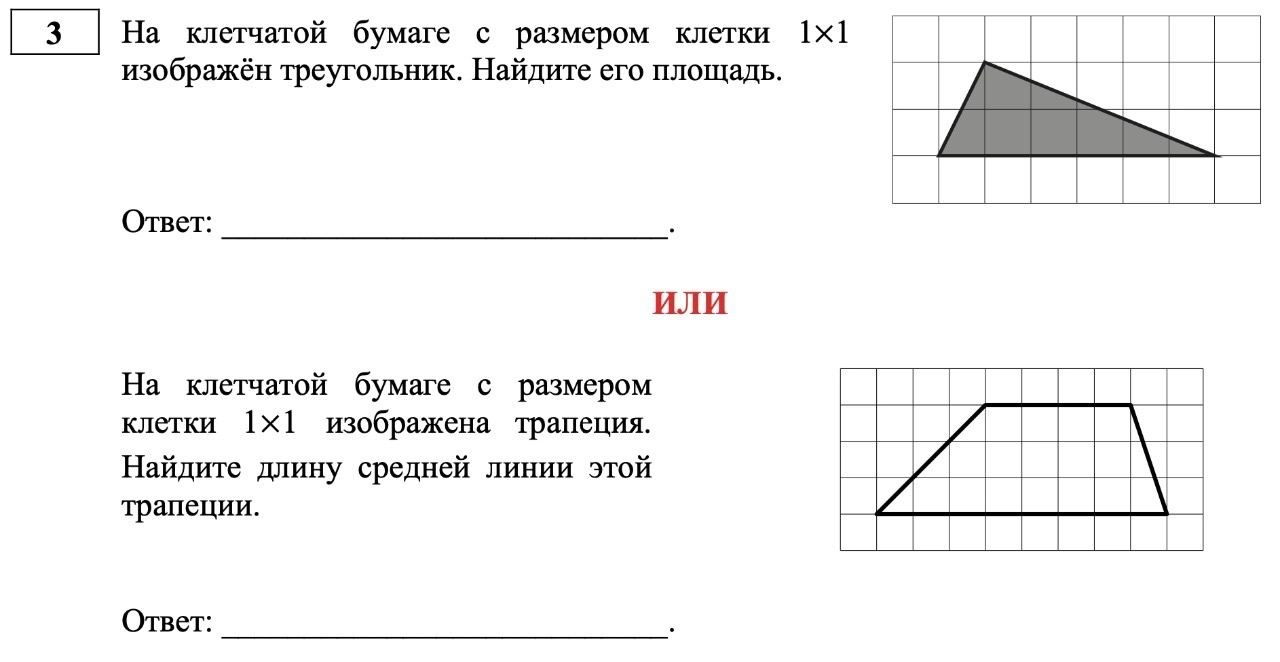
№ 3 – простейшей планиметрии на клеточках или координатной плоскости
Тип заданий, больше не встречающийся в перспективной модели ЕГЭ по математике 2022
Данные задания могут исключить из-за стабильно высокого процента решаемости, что противоречит изначальному принципу ЕГЭ – ранжировать абитуриентов.
Как теперь выглядит краткая часть
А что же тогда будет в новом экзамене?
Задание № 1
В перспективной модели на позиции №1 мы видим бывшее заданий № 5 – простейшее уравнение:
Простейшие уравнения в перспективной модели ЕГЭ по математике 2022
Задание № 2
На позиции № 2 – бывший № 4, задача по теории вероятности:
Задачи по теории вероятности, перспективная модель ЕГЭ по математике 2022
Задание № 3
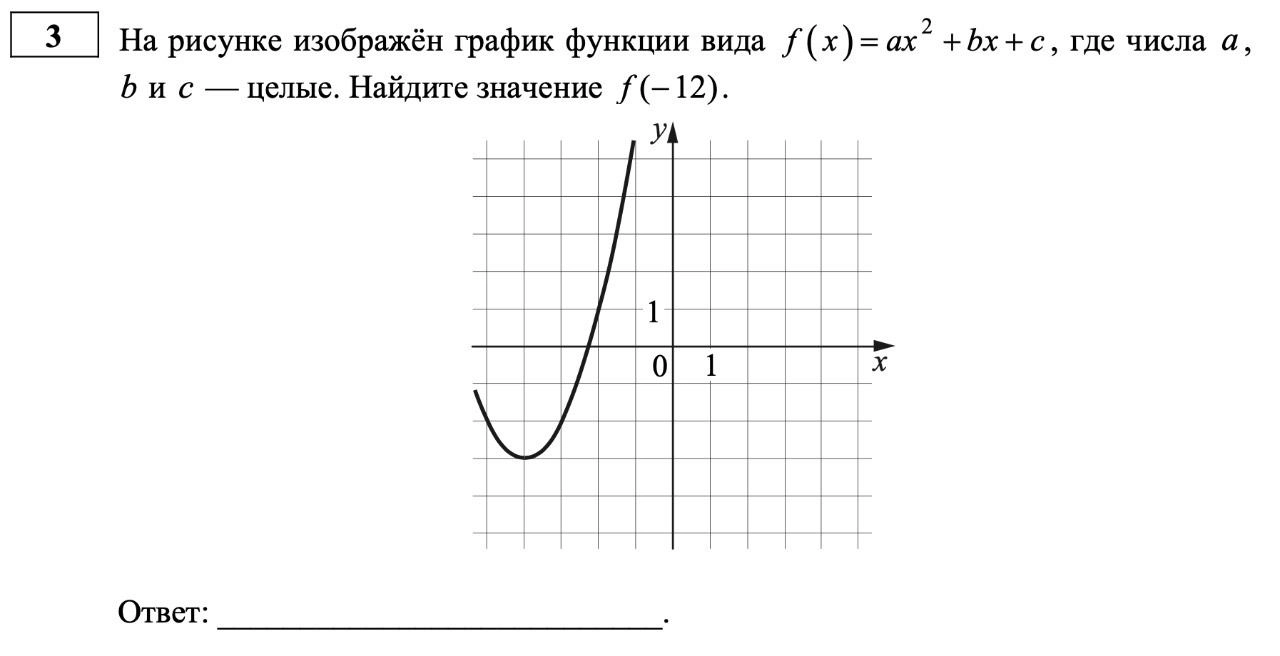
Вместо № 3 – новое задание на анализ функций. Это совершенно новый формат задания, хотя тема пересекается с ОГЭ, где обычно нужно сопоставить графики и формулы. Здесь же представлено более сложное задание на анализ.
Задание на графики, перспективная модель ЕГЭ по математике 2022
Задание № 4
Вместо бывшей задачи на вероятность в № 4 переместилась планиметрическая задача (раньше она была под № 6):
Планиметрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 5
В № 5 мы видим задание на выражение, которое раньше находилось под № 9. Раньше оно относилось к заданиям повышенной сложности. Сейчас же выражение относится к базовому уровню сложности, хотя содержательно ничего не изменилось.
Задание на выражение, перспективная модель ЕГЭ по математике 2022
Задание № 6
№ 6 стал стереометрической задачей, которая ранее была № 8:
Стереометрические задачи, перспективная модель ЕГЭ по математике 2022
Задание № 7
№ 7 – это один из двух номеров, которых не коснулись изменения. Как был номером на анализ функций, так им и остался (все прототипы сохранены).
Задание № 8
В № 8 переместилась прикладная задача (ранее № 10):
Прикладная задача, перспективная модель ЕГЭ по математике 2022
Задание № 9
№ 9 теперь будет текстовой задачей на движение, проценты или сплавы и смеси:
Задача на движение, перспективная модель ЕГЭ по математике 2022
Задание № 10
А № 10 – это новое задание из блока «Элементы комбинаторики, статистики и теории вероятностей» повышенного уровня сложности. Кстати, в 2021 в перспективной модели ОГЭ тоже были 2 задания из этого блока – в первой и второй частях. Однако такое изменение в итоге не было реализовано.
Задания из блока «Элементы комбинаторики, статистики и теории вероятностей»,
перспективная модель ЕГЭ по математике 2022
Задание № 11
В № 11 также планируется ввести совершенно новое задание на комплексные числа. Это новая тема, которая не освещалась ранее в ЕГЭ. По спецификации формат данного задания – «Вычисления и преобразования» повышенного уровня сложности:
Задание на комплексные числа, перспективная модель ЕГЭ по математике 2022
Задание № 12
И № 12 – второе задание, которое осталось неизменным. Это задание на экстремумы – поиск точек максимума/минимума и наибольшего/наименьшего значений функции.
Задания на экстремумы, перспективная модель ЕГЭ по математике 2022
Изменения в части с развёрнутым ответом
Что касается части с развёрнутым ответом, то здесь всего 3 ощутимых изменения.
1. Из № 13 убрали пункт б), посвящённый отбору корней на заданном промежутке
Скорее всего, это было сделано для того, чтобы было проще набрать частичные баллы.
Ранее ученики получали по одному баллу за каждый пункт и в случае неверного решения они теряли оба балла. Сейчас 1 балл можно получить при условии совершённой вычислительной ошибки, но верной последовательности всех действий. 2 балла – за полностью верное решение.
Задание № 13, перспективная модель ЕГЭ по математике 2022
2. № 15 – самые большие изменения
Когда-то в этом номере была система из уравнения и неравенства. Стоило такое задание 3 балла. Потом задание упростили до решения неравенства и понизили стоимость до 2 баллов. А сейчас мы видим, что эксперты хотят вернуться к прошлому опыту, добавить уравнение и детализировать критерии:
- неравенство, пункт а), решено – 1 балл;
- уравнение, пункт б), решено – 1 балл;
- система из неравенства и уравнения решена – 1 балл.
Задание № 15, перспективная модель ЕГЭ по математике 2022
Несмотря на детализацию, № 15 стал сложнее. Поэтому выросла его цена – задание снова будет стоить 3 балла. Вот мы и нашли новый, 33-й балл!
3. Меняют местами номера 16 и 17
Теперь экономическая задача будет под № 16, а планиметрия второй части под № 17.
Задание № 16, экономическая задача, перспективная модель ЕГЭ по математике 2022
Задание № 17, планиметрия, перспективная модель ЕГЭ по математике 2022
Оба задания, как и раньше будут стоить 3 балла. Меняют их местами, скорее всего, из-за того, что процент решаемости экономической задачи намного выше, чем у задачи на планиметрию.
Вектор изменений в ЕГЭ по математике
О чем же говорят предлагаемые изменения? Несмотря на стабильно невысокие результаты экзамена из года в год, ЕГЭ по математике скорее всего будет усложняться с 2022 года. Темы младшей и средней школы будут убирать, а на их место ставить темы старших классов. Сами задания также будут становиться сложнее.
Можно наблюдать огромную волну возмущений по поводу ЕГЭ, которая растёт из года в год, организации петиций и попытки собрать подписи по поводу отмены ЕГЭ. На самом деле, ЕГЭ нужно не отменять, а совершенствовать. Если экзамен будет не для набора баллов и поступления, а для подготовки к высшему образованию, то возмущений будет меньше. Ровно это и делают эксперты ФИПИ! Они стремятся повлиять на изучение тем в школах, чтобы важные для высшего образования вопросы не опускались в старших классах, а изучались глубоко и в полном объёме.
Но не спешите расстраиваться и пугаться. При качественной подготовке и вложенных усилиях возможно подготовиться к экзамену и получить высокий балл, так что всё в ваших руках! Не ждите озарения, начинайте готовиться уже сейчас!
Подготовиться к ЕГЭ на высокий балл вы можете вместе с нашими преподавателями. Они поделятся с вами всеми секретами сдачи экзамена и научат быстро и правильно решать самые сложные задания. Приходите к нам на бесплатный пробный урок и начните готовиться к ЕГЭ прямо сейчас!