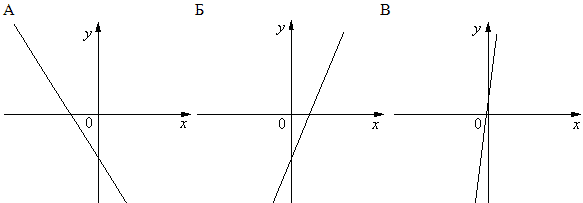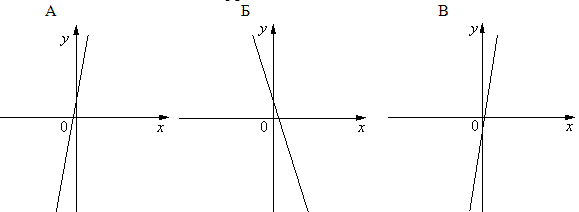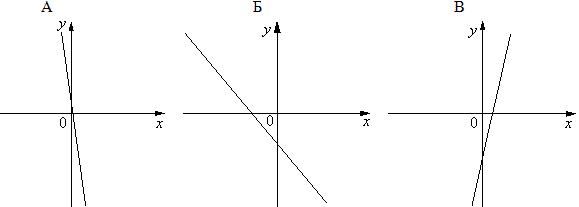Муниципальное
общеобразовательное учреждение
«Средняя
общеобразовательная школа» п.Новый Урал
Согласовано:_________
Утверждаю: _________
Зам.директора
по УВР Директор школы МОУ СОШ п.Новый
Ковалева
Т.А. Урал Кормилицын А.А.
________________2018г
________________2018г
Переводной
экзамен по математике в 8 классе
Разработчик:
Клочкова М.М.
учитель
математики
2017
— 2018 уч.г.
Вариант
1
Часть
1
Модуль
«Алгебра»
1.Одна из точек, отмеченных на
координатной прямой, соответствует числу . Какая это точка?
1) М; 2) N; 3)
Р; 4) Q.
Ответ:________
2. Найдите значение выражения .
Ответ:________
3.Решите уравнение: — 25 =0. Если уравнение
имеет более одного корня, в ответе запишите больший из корней.
Ответ:________
4.Найдите значение выражения:
꞉

= 8.
Ответ:________
5.Установите соответствие между графиками
функций и формулами, которые их задают.
Графики
Формулы :
А) у = ; Б)
у = — ; В)
у = — .
В
таблице под каждой буквой укажите соответствующий номер.
Ответ:
6. При
работе фонарика батарейка постепенно разряжается и напряжение в электрической
цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от
времени работы фонарика. На горизонтальной оси отмечается время работы фонарика
в часах, на вертикальной оси – напряжение в вольтах.
Определите по
рисунку, через сколько часов работы фонарика напряжение уменьшится до 0,6
вольт.

7. На диаграмме показан возрастной состав
населения Китая. Определите по диаграмме, население какого возраста составляет
более 50٪ от всего населения.
1) 0 – 14 лет 2) 15 – 50 лет
3) 51 – 64 года 4) 65 лет и более
В
ответе запишите номер выбранного варианта.
Ответ:_______
Модуль
«Геометрия»
8.В
треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в
градусах.
Ответ:_______
9.Сторона треугольника равна 14, а
высота, проведенная к этой стороне, равна 31. .
Найдите площадь треугольника.
Ответ:________
10. На клетчатой бумаге с размером клетки
1 × 1 изображен ромб. Найдите длину его большей диагонали.

11.На
рисунке изображено колесо с пятью спицами. Сколько спиц в колесе, в котором
угол между любыми соседними спицами равен 60°.

12.
Какие из следующих утверждений верны?
1)
Боковые стороны любой трапеции равны;
2)
Через любую точку, лежащую вне окружности, можно провести две касательные к
этой окружности;
3)
Площадь квадрата равна произведению его диагоналей.
В
ответе запишите номер выбранных утверждений без пробелов, запятых и других
дополнительных символов.
Ответ:_________
Часть
2
Модуль
«Алгебра»
1.Решите
систему уравнений:
2.
Решите
уравнение +
=
Модуль
«Геометрия»
1. Высота
АН ромба АВСD делит сторону СD
на отрезки DН = 16 и
СН = 4. Найдите высоту
ромба.
2. АВ
и СД пересекаются в точки О, ОВ = ОС и угол В равен углу С. Докажите равенство
треугольников АОС и DОВ.
Вариант
2
Модуль
«Алгебра»
1.Между какими числами заключено число ?
1) 7 и 8; 2)20 и 22; 3) 58 и
60; 4) 3и 4.
Ответ:_______
2. Найдите значение выражения:
.
Ответ:_______
3. Решите уравнение: + 20х = 0. Если уравнение
имеет более одного корня, в ответе запишите меньший из корней.
Ответ:_______
4. Найдите значение выражения:

а = 3.
Ответ:_______
5.Установите соответствие между графиками
функций и формулами, которые их задают
Графики
Формулы
1) у
= — 2 2) у = х – 2 3) у = —
2х
В таблице под каждой буквой укажите
соответствующий номер.
Ответ:
6. При работе
фонарика батарейка постепенно разряжается и напряжение в электрической цепи
фонарика падает. На рисунке показана зависимость напряжения в цепи от времени
работы фонарика. На горизонтальной оси отмечается время работы фонарика в
часах, на вертикальной оси – напряжение в вольтах.
Определите по
рисунку, каким было напряжение через 2 часа работы фонарика. Ответ дайте в
вольтах.

7.На диаграмме показано содержание
питательных веществ в сливочном мороженом. Определите по диаграмме, содержание
каких веществ превосходит 25٪ .

1) Белки
2) жиры 3) углеводы 4) прочее
В
ответе запишите номера выбранных ответов без пробелов, запятых и других
символов.
Ответ:_________
Модуль
«Геометрия»
8. В
треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в
градусах.
Ответ:_________
9.Найдите
площадь параллелограмма на рисунке.
Ответ:__________
10.Две сосны растут на расстоянии 15м одна
от другой. Высота одной сосны 30м, а другой – 22м. Найдите расстояние (в метрах)
между их верхушками.
Ответ:___________
11.
В треугольнике АВС известно, что АС =32. ВМ – медиана, ВМ = 23. Найдите АМ. 
12.
Какие из следующих утверждений верны?
1)
Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к
прилежащему к этому углу катету.
2)
У любой трапеции основание параллельны.
3)
Всегда один из двух смежных углов – острый, а другой тупой.
В
ответе запишите номер выбранного утверждения.
Ответ:__________
Часть
2
Модуль
«Алгебра»
1. Сократите
дробь: 
2. Решите
уравнение +
— 12 = 0
Модуль
«Геометрия»
1. В
прямоугольном треугольнике АВС с прямым углом С известны катеты: АС = 6 см; ВС
= 8 см. Найдите медиану СК этого треугольника.
2. Докажите,
что отрезки касательных, проведенных к окружности из одной точки, равны.
Вариант
3
Часть
1
Модуль
«Алгебра»
1.Найдите значение выражения 2,3 ∙
7,5.
Ответ:____________
2.Какие из данных чисел принадлежит
промежутку?
1) 2)
3)
4)
Ответ:____________
3. Решите уравнение ( х – 6)
(4х – 6)= 0. . Если уравнение имеет более одного корня, в ответе
запишите больший из корней.
Ответ:____________
4. Найдите значение выражения ∙

а = 9,2 b
= 18.
Ответ:____________
5. Установите соответствие между графиками
функций и формулами, которые их задают.
Графики
Формулы
В таблице под каждой буквой укажите
соответствующий номер.
Ответ:
6.При работе фонарика батарейка
постепенно разряжается, и напряжение в электрической цепи фонарика падает. На
рисунке показана зависимость напряжения в цепи от времени работы фонарика. На
горизонтальной оси отмечается время работы фонарика в часах, на вертикальной
оси – напряжение в вольтах. Определите по рисунку, на сколько вольт упадет
напряжение за 6 часов работы фонарика.
Ответ:___________
7.
Модуль
«Геометрия»
8. В треугольнике два угла равны 29° и 71°.
Найдите его третий угол. Ответ дайте в градусах.
Ответ:___________
9.Катеты прямоугольного треугольника равны
16 и 30. Найдите гипотенузу этого треугольника.
Ответ:___________
10.На клетчатой бумаге с размером клетки
1×1 изображена фигура. Найдите её площадь.

11. Сторона АС треугольника АВС проходит
через центр описанной около него окружности. Найдите угол С , если угол А =
30°. Ответ дайте в градусах.

12.Какие из следующих утверждений верно?
1)
Всегда один из двух смежных углов – острый, а другой тупой.
2)
Площадь квадрата равна произведению двух его смежных сторон.
3)
Все хорды одной окружности равны между собой.
В
ответе запишите номер выбранного варианта ответа.
Ответ:___________
Часть
2
Модуль
«Алгебра»
1. 1.Решите
систему уравнений:
2.
Решите уравнение +
=
Модуль
«Геометрия»
1. В
треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между
высотой ВН и биссектрисой ВД.
2. АВ
и СД пересекаются в точки О, ОВ = ОС и угол В равен углу С. Докажите равенство
треугольников АОС и DОВ.
Вариант
4
Часть
1
Модуль
«Алгебра»
1. .Найдите значение выражения .
Ответ:___________
2. Какие из данных чисел принадлежит
промежутку?
1) 2)
3)
4)
Ответ:___________
3.Решите уравнение 4х
– 3 = — 6х -4.
Ответ:___________
4.Найдите значение выражения 
Ответ:___________
5. Установите соответствие
между функциями и их графиками.
Функции
Графики
В таблице под каждой буквой укажите
соответствующий номер.
Ответ:
6.На графике изображена зависимость
атмосферного давления от высоты над уровнем моря. По горизонтали указана высота
над уровнем моря в километрах, по вертикали – атмосферное давление в
миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если
барометр, находящийся в корзине шара, показывает давление 300 миллиметров
ртутного столба?
Ответ:_______
7.
Модуль
«Геометрия»
8. В треугольнике два угла равны 25° и 85°.
Найдите его третий угол. Ответ дайте в градусах.
Ответ:_________
9.Найдите площадь ромба, если его
диагонали равны 5 и 6.
Ответ:__________
10.
На рисунке изображено колесо с пятью спицами. Сколько спиц в колесе, в котором
угол между любыми соседними спицами равен 40°.

11. .На клетчатой бумаге с размером клетки
1×1отмечены три точки: А, B
и С. Найдите расстояние от точки А до прямой ВС.
. 
12.Какое из следующих утверждений верно?
1)
Площадь любого параллелограмма равна произведению длин его сторон.
2)Треугольник
со сторонами 1, 2, 4 существует.
3)
У любой трапеции основания параллельны.
В ответе запишите номер выбранного
утверждения.
Ответ:_________
Часть
2
Модуль
«Алгебра»
1. Сократите дробь:

2. Решите уравнение +
— 12 = 0
Модуль
«Геометрия»
1. В равнобедренной трапеции один из углов
равен 45°, а высота, проведенная из вершины тупого угла, делит большее
основание на отрезки 4 см и 12 см. Найдите площадь трапеции.
2.Докажите, что отрезки касательных,
проведенных к окружности из одной точки, равны.
Вариант
5
Часть
1
Модуль
«Алгебра»
1. Найдите значение выражения 2,1 ∙
9,6.
2.В таблице дано соответствие размеров
женских платьев в Белоруссии, России, Англии и Европейском Союзе.
Какому российскому размеру соответствует
44-й размер платья в Европейском Союзе?
38
2) 88 3) 50 4) 16
Ответ:_______
3.Решите уравнение (х
– 5)(х + 3) = 0 Если уравнение имеет более одного
корня, в ответе запишите меньший из корней.
Ответ:________
4.Между какими числами заключено число ?
1)
2 и 3 2) 5 и 6 3) 12 и 14 4) 26 и 28
Ответ:________
5. Установите соответствие между графиками
функций и формулами, которые их задают.
Графики
Формулы
В таблице под каждой буквой укажите
соответствующий номер.
Ответ:
6.На графике изображена зависимость
атмосферного давления от высоты над уровнем моря. На горизонтальной оси
отмечена высота над уровнем моря в километрах, на вертикальной – давление в
миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное
давление равно 400 миллиметрам ртутного столба. Ответ дайте в километрах.

Ответ:__________
7.На диаграмме показано содержание
питательных веществ в твороге. Определите по диаграмме, содержание каких
веществ наименьшее.
1) белки
2) жиры 3) углеводы 4) прочее
В ответе запишите
номер выбранного варианта.
Ответ:_________
Модуль
«Геометрия»
8. В треугольнике два угла равны 65° и 85°.
Найдите его третий угол. Ответ дайте в градусах.
Ответ:__________
9.Пожарную лестницу длиной 10м приставили
к окну третьего этажа дома. Нижний конец лестницы отстоит от стены на 6 м. На
какой высоте расположено окно? Ответ дайте в метрах.

10.Сторона треугольника равна 18, а
высота, проведенная к этой стороне, равна 17. Найдите площадь треугольника.
Ответ:_________
11. На клетчатой бумаге с размером клетки
1×1 изображена фигура. Найдите её площадь.

12.Какие из следующих утверждений верны?
1)
Смежные углы равны.
2)
Площадь квадрат равна произведению двух его смежных сторон.
3)
Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
В ответе запишите номера выбранных
утверждений без пробелов, запятых и других дополнительных знаков.
Ответ:_________
Часть
2
Модуль
«Алгебра»
1.Сократите дробь 
2.Решите систему уравнений
Модуль
«Геометрия»
1.В равнобедренном треугольнике АВС с
основанием АС, внешний угол при вершине С равен 123°.Найдите величину угла ВАС.
Ответ дайте в градусах.
2.Докажите, что отрезки касательных,
проведенных к окружности из одной точки, равны.
Бланк
ответов
Заполнять
ручкой ЗАГЛАВНЫМИ ПЕЧАТНЫМИ БУКВАМИ
|
Фамилия |
|
||||||||||||||||||
|
Имя |
|
||||||||||||||||||
|
Отчество |
|
||||||||||||||||||
|
ЗАПРЕЩЕНЫ |
|||||||||||||||||||
Ответ Замена ошибочного ответа
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
Ответы :
|
№ |
Вариант |
|
Часть |
|
|
1 |
1 |
|
2 |
1 |
|
3 |
5 |
|
4 |
7 |
|
5 |
231 |
|
6 |
9 |
|
7 |
2 |
|
8 |
68 |
|
9 |
217 |
|
10 |
12 |
|
11 |
6 |
|
12 |
2 |
|
Часть Модуль |
|
|
1 |
(1;8) |
|
2 |
0; 6 |
|
Модуль |
|
|
1 |
12 |
|
2 |
Доказательство: ОВ
|
|
№ |
Вариант |
|
Часть |
|
|
1 |
1 |
|
2 |
2 |
|
3 |
— 4 |
|
4 |
2 |
|
5 |
132 |
|
6 |
1,2 |
|
7 |
34 |
|
8 |
74 |
|
9 |
100 |
|
10 |
17 |
|
11 |
16 |
|
12 |
2 |
|
Часть Модуль |
|
|
1 |
12,5 |
|
2 |
— |
|
Модуль |
|
|
1 |
5 |
|
2 |
Доказательство: Соединим АО ⇓ АС |
|
№ |
Вариант |
|
Часть |
|
|
1 |
17,25 |
|
2 |
3 |
|
3 |
6 |
|
4 |
4,5 |
|
5 |
132 |
|
6 |
0,6 |
|
7 |
13 |
|
8 |
80 |
|
9 |
34 |
|
10 |
9 |
|
11 |
60 |
|
12 |
2 |
|
Часть Модуль |
|
|
1 |
(2;1) |
|
2 |
0;6. |
|
Модуль |
|
|
1 |
15 |
|
2 |
Доказательство: ОВ
|
|
№ |
Вариант |
|
Часть |
|
|
1 |
1 |
|
2 |
4 |
|
3 |
-0,1 |
|
4 |
3,5 |
|
5 |
321 |
|
6 |
7 |
|
7 |
23 |
|
8 |
70 |
|
9 |
15 |
|
10 |
9 |
|
11 |
2 |
|
12 |
3 |
|
Часть Модуль |
|
|
1 |
12,5 |
|
2 |
— |
|
Модуль |
|
|
1 |
48 |
|
2 |
Доказательство: Соединим АО ⇓ АС |
|
№ |
Вариант |
|
Часть |
|
|
1 |
20,16 |
|
2 |
3 |
|
3 |
— 3 |
|
4 |
2 |
|
5 |
132 |
|
6 |
5 |
|
7 |
3 |
|
8 |
30 |
|
9 |
8 |
|
10 |
153 |
|
11 |
10 |
|
12 |
23 |
|
Часть Модуль |
|
|
1 |
16 |
|
2 |
(2,2; 5) |
|
Модуль |
|
|
1 |
57 |
|
2 |
Доказательство: Соединим АО ⇓ АС |
Пояснительная записка
Работа содержит 16 заданий курса алгебры и геометрии .
Каждый из двух вариантов содержит две части.
Часть 1 — 12 заданий базового уровня
Часть 2 — 4 задачи высокого уровня, где требуется написать развернутое решение.
Критерии оценивания: За каждый верный ответ 1-й части начисляется 1 балл, за каждое верное решение задачи 2-й части – 2 балла. Максимальное количество баллов – 20. Оценка ставится в зависимости от набранных баллов:
|
Баллы |
Оценка |
|
0-6 |
2 |
|
7-10 |
3 |
|
11-15 |
4 |
|
16-20 |
5 |
Вариант № 1
Часть 1
1. Вычислите (32)4 : (35 × 32)
2. Выполните умножение: (с – 5) (c+1)
3. Решением системы уравнений: является пара чисел:
а) (2; 3); б) (- 2; 3); в) (2; — 3); г) (- 2; — 9); д) (- 2; 9).
4. Решите уравнение 3(5 – 2х) – 4 = 4 – 5х
5. Решите систему линейных уравнений:
6. Постройте график функции у=2х+2.
7. Упростите выражение (х – 2)2 + (х – 1)(х +1 )
8. Два угла треугольника равны 300 и 530. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, АВ=5см. Найдите ВС.
10. Дано: Найдите:
.
C
O
B
11. Выберите верное утверждение:
1. Если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180°,то такие прямые параллельны.
2. Если угол равен 47°, то смежный с ним равен 153°.
3. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
4. Через любые две точки проходит бесконечно много прямых.
12. В треугольнике АВС АВ=ВС, ВЕ – медиана треугольника. АВЕ = 400. Найти ∠ АВС.
Часть 2
13.Решите уравнение: х2 + 4х+3=0
14. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч. Найдите собственную скорость лодки и скорость течения реки.
15. Дано: Найти:
m
n
1
2
3
4
A
C
B
16. В треугольнике СКЕ стороны СЕ и КE равны, биссектрисы СМ и КН пересекаются в точке А. Докажите, что треугольники КАМ и САН равны.
Вариант № 2
Часть 1
1. Вычислите 26 * (22)5 : 213
2. Выполните умножение: (а – 3) (а + 4)
3. Решением системы уравнений: является пара чисел:
а) (5; 2); б) ( 5; — 2); в) (- 5; — 2); г) (- 5; — 7); д) (5; — 7).
4. Решите уравнение 6(4 – х) + 4х = 3+х
5. Решите систему уравнений:
6. Постройте график функции у= -2х-2.
7. Упростите выражение: ( х + 3)2 + (х – 1) (х +1)
8. Два угла треугольника равны 400 и 380. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, ВС=12см. Найдите АВ.
10. Дано: Найдите:
.
C
O
B
A
11. Выберите верное утверждение:
1. Если две прямые параллельны третьей, то они пересекаются.
2. В равнобедренном треугольнике медиана, проведенная к боковой стороне, является высотой и биссектрисой.
3. Если при пересечении двух прямых секущей сумма соответственных углов равна 180°,то такие прямые параллельны.
4. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
12. В треугольнике АВС АВ=ВС, ВК –высота треугольника. АВС = 1300. Найти ∠ КВС.
Часть 2
13.Решите уравнение: х2 – 4х+3=0
14.Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.
15. Дано: Найти:
A
B
C
b
a
1
2
3
4
16. В равнобедренном треугольнике КЕС с основанием СК медианы СМ и КН пересекаются в точке А. Докажите, что треугольник КАС – также равнобедренный.
Переводные экзамены в школе: какие правила
22.04.2022
Многие мамы и папы еще помнят, как сдавали в школе экзамены, чтобы перейти из класса в класс, как волновались и готовились. Кажется, с введением ЕГЭ и ОГЭ переводные экзамены стали неактуальны и в школах больше не проводятся. Однако некоторые учебные заведения все еще пользуются такой формой контроля. Разбираемся, законно ли это и что делать, если ребенок завалил такую работу.
Что такое современные переводные экзамены
Современный переводной экзамен представляет собой форму промежуточного или итогового контроля успеваемости учеников. То есть, проще говоря, это контрольная работа. Некоторые школы дают ее обучающимся 5-8-ых, а также 10-х классов. Выпускники 9 и 11 классов переводной экзамен сдавать не могут, у них совсем другая форма контроля — ОГЭ и ЕГЭ.
Могут ли школы сейчас проводить такие экзамены
В статье 58 “Закона об образовании РФ” говорится: “Освоение образовательной программы <…> сопровождается промежуточной аттестацией обучающихся, проводимой в формах, определенных учебным планом, и в порядке, установленном образовательной организацией”. Это значит, что школы могут проводить промежуточный контроль знаний обучающихся в той форме, в которой посчитают нужным, в том числе и в форме экзамена. Однако, хотя экзамен и называется переводным, переход подростка из класса в класс зависит не от его результата, а от отсутствия аттестации по какому-либо предмету.
Может ли школа вводить переводные экзамены для поступления в профильный класс
В профильных классах ребята имеют возможность углубленно изучать предметы, которыми они интересуются или которые в скором времени собираются сдавать. Из-за этого желающих попасть в такие классы набирается достаточно много. Может ли школа в этом случае регулировать набор путем введения переводного экзамена?
По правилам набор в профильный класс производится в старшей школе, то есть в 10 классе.
Как уже говорилось выше, выпускники 9 класса переводные экзамены сдавать не нужно, у них уже есть ОГЭ. То есть отбор в профильный класс не может производиться на основаниях дополнительно экзамена, введенного школой. Если учитель заставляет пятиклассника сдавать профильный экзамен по математике, чтобы перевести его в математический класс, ребенок имеет право отказаться.
Довольно часто “профильным” называют класс, в который просто отбирают детей со способностями к определенным предметам и профиль проявляется в усложненной программе и сетке дополнительных курсов. Многих родителей такое устраивает, однако законных оснований делать профильный класс, скажем, в 6 или 7 классе у школы нет.
Но их всех правил есть исключения. Например, проект «Математическая вертикаль», куда допускается отбор. И разумеется, при общем согласии родительского сообщества и школы переводные экзамены проводят и угрожают неаттестацией и без всяких проектов.
Плюсы и минусы переводных экзаменов
Само выражение “переводной экзамен” звучит устрашающе, но у этого мероприятия есть как минусы, так и плюсы.
Плюсы переводных экзаменов:
- Возможность подростку актуализировать знания. Контрольные мероприятия направлены не только на проверку обучающихся, но и на мотивацию повторить уже пройденный материал, систематизировать и закрепить его.
- Повышение стрессоустойчивости подростка. Конечно, обучающиеся испытывают некоторое волнение, даже когда пишут обычную проверочную или контрольную работу. Тем более они будут нервничать во время экзамена. Однако написание переводного экзамена позволит подросткам морально подготовиться к более серьезным испытаниям.
- Тренировка перед настоящим экзаменом. Ведь ОГЭ и ЕГЭ — это не просто знание теории и даже не только моральная подготовка. Это еще и определенная регламентированная процедура: пристальное наблюдение за дисциплиной, строгий тайминг и т.д. На переводной работе подростки могут познакомиться с обстановкой, тогда реальный экзамен не будет для них настолько стрессовой ситуацией.
Минус:
Дополнительное волнение для подростка. В школе обучающиеся и так нагружены: уроки, домашние задания, проверочные работы, внеклассные мероприятия и т.д. Введение переводного экзамена как формы промежуточного контроля еще больше увеличат нагрузку.
Родителям необходимо помочь подросткам получить максимальные преимущества от переводного экзамена, поддержать обучающихся, чтобы излишнее волнение не переросло в страх и не помешали успешно пройти это испытание.
На что влияет оценка за переводной экзамен
Как было сказано выше, результат переводного экзамена оказывает мало влияния. Но зато итоговая оценка по предмету от него может зависеть. В спорных случаях результат экзамена может как повысить, так и понизить годовую оценку. Например, если ученик в двух четвертях имел по предмету четверки и в двух — пятерки, полученная отличная оценка на экзамене решит итог в пользу ученика — за год он получит пятерку.
Однако возможна и другая ситуация: если ребенок, которому какой-то предмет не дается, имеет по нему невысокие оценки и заваливает переводную работу, то ему действительно может грозить неаттестация.
Что делать, если ребенок завалил переводной экзамен?
- Не паниковать. Плохая оценка за переводной экзамен не означает автоматического оставления на второй год. Школа обязательно дает шанс пересдать неудачную работу.
- Успокойте ребенка. Он переживает не меньше вас. К огорчению от неудачи может примешиваться чувство вины — подросток чувствует, что не оправдал надежд, расстроил родителей, отчаяние — ему кажется, у него никогда не получится преуспеть в предмете. Поддержите ребенка, дайте понять, что вы на его стороне и готовы ему помочь.
- Помогите подготовиться к пересдаче. Разберитесь вместе с ребенком, какие темы вызывают у него наибольшие затруднения. Затем составьте график: в какие дни сколько времени он будет уделять каждой. Если ребенок недостаточно собранный, проследите, как он соблюдает установленный график, тогда к переэкзаменовке он будет чувствовать себя гораздо увереннее.
В общем и целом, в большинстве случаев переводные экзамены в школе — это договоренность родителей и школы о правилах игры. Большую часть решений, принятых на основании такого экзамена, можно при желании опротестовать.
Листайте также
Как уладить конфликт с классным руководителем
Как помочь ребенку адаптироваться в новой школе или коллективе. Стресс при смене школы
1 вариант
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа 0,098; –0,02; 0,09; 0,11. Какой точкой
изображается число 0,09? Запишите номер ответа.
1) А; 2) В; 3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,4; 2) 0,5; 3) 0,6; 4) 0,7.
4. Решите уравнение 2 – 3(2х + 2) = 5 – 4х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b<0; 2) k>0, b<0; 3) k>0,
b>0. В ответе укажите последовательность
цифр.
6. Найдите значение выражения при а = 0,2, b = 1,5.
Запишите ответ.
7. Вычислите: .
Модуль Геометрия
8. Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Смежные углы равны.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним
равен 108°.
4) Если две стороны и угол между ними одного
треугольника равны соответственно двум сторонам
и углу между ними другого треугольника, то такие
треугольники равны.
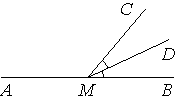
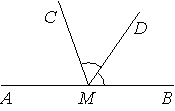
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC=24°.
Найдите угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 68. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. Мотоциклист проехал 19 километров за 15 минут.
Сколько километров он проедет за 18 минут, если
будет ехать с той же скоростью?
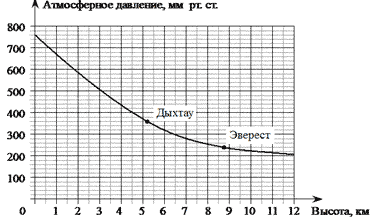
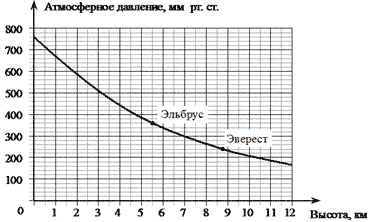
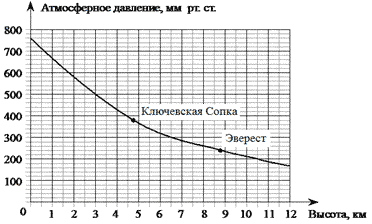
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Дыхтау?
13. На диаграмме показано содержание
питательных веществ в молочном шоколаде.
Определите по диаграмме, содержание каких
веществ превосходит 25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 3 часа,
вернулись обратно через 5 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
3 км/ч, а собственная скорость лодки 6 км/ч?
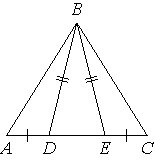
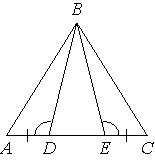
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
углы АDB и BEC равны (см. рисунок).
Оказалось, что отрезки AЕ и CD тоже
равны. Докажите, что
треугольник АВС — равнобедренный.
2 вариант
Часть 1
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа 0,508; 0,85; -0,05; 0,058. Какой точкой
изображается число 0,058? В ответе укажите номер
правильного варианта.
1) А; 2) В;3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,3; 2) 0,4; 3) 0,5; 4) 0,6.
4. Решите уравнение 8 – 5(2х – 3) = 13 – 6х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b>0; 2) k>0, b>0; 3) k>0,
b<0. В ответе укажите последовательность
цифр.
6.Найдите значение выражения при а = 0,3, b =
0,2.Запишите ответ.
7. Вычислите: .
Модуль Геометрия
8.Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Если угол равен 47°, то смежный с ним равен 153°.
2) Если две прямые перпендикулярны третьей
прямой, то эти две прямые параллельны.
3) Через любую точку проходит ровно одна прямая.
4) Если сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне и
прилежащим к ней углам другого треугольника, то
такие треугольники равны.
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC =
48°. Найдите угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 88. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. За 20 минут велосипедист проехал 7 километров.
Сколько километров он проедет за 35 минут, если
будет ехать с той же скоростью?
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Эльбруса?
13. На диаграмме показано содержание
питательных веществ в мороженом. Определите по
диаграмме, содержание каких веществ превосходит
25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 2 часа,
вернулись обратно через 6 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
3 км/ч, а собственная скорость лодки 6 км/ч?
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
отрезки AD и CE равны (см. рисунок).
Оказалось, что отрезки BD и BE тоже
равны. Докажите, что треугольник АВС —
равнобедренный.
3 вариант
Часть 1
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа –0,74; –0,047; 0,07; –0,407. Какой точкой
изображается число ?0,047? В ответе укажите номер
правильного варианта.
1) А; 2) В; 3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,1; 2) 0,2; 3) 0,3; 4) 0,4.
4. Решите уравнение 11 – 7(х + 2) = 5 – 2х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b<0; 2) k<0, b>0; 3) k>0,
b<0. В ответе укажите последовательность
цифр.
6. Найдите значение выражения при а = 0,5, b =
0,1.Запишите ответ.
7.Вычислите: .
Модуль Геометрия
8. Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Если три стороны одного треугольника
соответственно равны трём сторонам другого
треугольника, то такие треугольники равны.
2) Сумма вертикальных углов равна 180о.
3) Через точку, не лежащую на данной прямой,
можно провести прямую, перпендикулярную этой
прямой.
4) Если угол равен 30о, то смежный с ним
равен 60о.
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC=41°. Найдите
угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 84. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. Автомобиль проехал 17 километров за 15 минут.
Сколько километров он проедет за 18 минут, если
будет ехать с той же скоростью?
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Ключевской Сопки?
13. На диаграмме показано содержание
питательных веществ в сгущённом молоке.
Определите по диаграмме, содержание каких
веществ превосходит 25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 3 часа,
вернулись обратно через 5 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
2 км/ч, а собственная скорость лодки 8 км/ч?
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
отрезки AD и CE равны (см. рисунок).
Оказалось, что углы АDB и BEC тоже равны.
Докажите, что треугольник АВС-равнобедренный.
Приложение 1
Приложение 2
Переводной экзамен за курс 8 класса
по предмету «Математика»
Инструкция по выполнению работы
Общее время на выполнение работы — 150 минут.
Характеристика работы. Всего в работе 17 заданий, из которых 12 заданий базового уровня (часть 1), 5
заданий повышенного и высокого уровня сложности (часть 2). Работа состоит из двух модулей: «Алгебра» и
«Геометрия»
Модуль «Алгебра» содержит 9 заданий: в 1 части – 6 заданий; в 2 части — 3 задания (задания
повышенного и высокого уровня сложности). Модуль «Геометрия» содержит 8 заданий: 6 заданий в 1 части;
в 2 части — 2 задания (задание повышенного уровня сложности).
Ответы к заданиям 5, 7 запишите в виде цифры или последовательности цифр, которые
соответствует номеру правильного ответа. Эту цифру или цифры запишите в ответе к заданию. В остальных
заданиях 1 части ответом является число или числа, которые надо записать в ответе. Если получилась
обыкновенная дробь, переведите ее в десятичную. Если ошиблись, зачеркните и напишите верный ответ.
Сначала выполняются задания 1 части. Начните с того модуля, который у вас вызывает меньше
затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задания, которые не
удается выполнить сразу, и переходите к другим заданиям, если останется время, можно к ним вернуться.
Решения заданий части 1 и 2 выполняются письменно на листе со штампом необходимо
представить полное обоснованное решение и записать краткий ответ на вопрос задачи. Текст задания
переписывать не нужно, достаточно только указать номер задания.
Баллы при выполнении заданий суммируются.
Устанавливается следующий рекомендуемый минимальный критерий:
5 баллов, набранные по всей работе, из них – не менее 4 баллов по модулю «Алгебра», не менее 1 балла
по модулю «Геометрия». Только выполнение всех условий минимального критерия даёт ученику право на
получение положительной отметки.
За каждое верно выполненное задание выставляется 1 балл.
Желаем успеха
Переводной экзамен за курс 8 класса
по предмету «Математика»
1 вариант
1 часть
Модуль «Алгебра»
1.Выполните действия: а)
а
х
х
а
; б)
х
х
х
2.Упростить выражение: а) 3
5
·
; б) 5 — 3√7 + √63.
3.Найти значение выражения
х
у
, если х = 10 и у = —6.
4.Решить уравнение 5х
2
– 16х + 3 = 0.
6.Решить систему уравнений
х у
х у
Модуль «Геометрия»
7.Выберите верные утверждения:
1)Периметр четырёхугольника – это сумма длин всех его сторон.
2)Ромб – это параллелограмм, у которого все углы прямые.
3)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
4)Косинус острого угла прямоугольного треугольника – это отношение противолежащего (к этому углу)
катета к гипотенузе.
5)Вектор – это направленный отрезок.
8.Гипотенуза прямоугольного треугольника равна 29. Один из катетов равен 21. Найти другой катет.
9. а (1;2),
(-3; 0). Найти а +
.
10.Дан прямоугольный треугольник АВС, ∟С = 90°. АВ = 13, АС = 5. Найти косинус угла А.
11.Дана трапеция, которая имеет основания 4 и 11. Найти среднюю линию трапеции.
12.
2 часть
Модуль «Алгебра»
13.Расположить в порядке возрастания 5√2; 7; 3√8; 4√3.
14.Упростить выражение: а
а
а
а
а
а
15.Решить задачу: а) Длина прямоугольника на 5 см больше его ширины. Найти длину прямоугольника,
если при её уменьшении на 1 см и увеличении ширины на 2 см, площадь прямоугольника стала 48 см
2
.
б)Найдите три последовательных натуральных числа, сумма квадратов которых равна 50.
Модуль «Геометрия»
16.Найдите координаты вершин треугольника МРК, образованного средними линиями треугольника АВС,
если А (5; —1), В (—3; 7), С ( 1;-3).
17. Найти периметр прямоугольника, если одна из его сторон равна 15, а диагональ равна 17.
2 вариант
1 часть
Модуль «Алгебра»
1.Выполните действия: а)
; б)
2.Упростить выражение: а) 2
0
·
; б) 7 + 2√5 — √20.
3.Найти значение выражения
, если a = 12 и b = —5.
4.Решить уравнение 3х
2
+ 5х — 2 = 0.
6. Решить систему уравнений
х у
х у
Модуль «Геометрия»
7.Выберите неверные утверждения:
1)Периметр четырёхугольника – это сумма длин всех его сторон.
2)Ромб – это параллелограмм, у которого все углы прямые.
3)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
4)Синус острого угла прямоугольного треугольника – это отношение прилежащего (к этому углу) катета к
гипотенузе.
5)Вектор – это направленный отрезок.
8.Гипотенуза прямоугольного треугольника равна 29. Один из катетов равен 20. Найти другой катет.
9. а (1;2),
(-3; 0). Найти а —
10.Дан прямоугольный треугольник АВС, ∟С = 90°. АВ = 13, АС = 5. Найти синус угла В.
11.Дана трапеция, которая имеет основания 8 и 13. Найти среднюю линию трапеции.
2 часть
Модуль «Алгебра»
13.Расположить в порядке возрастания √6; 2√3; 3√2; √5.
14.Упростить выражение: х
х
х
х
х
х
15.Решить задачу: а)Сторона первого квадрата на 5 см меньше второго, а площадь первого на 65 см
2
меньше
площади второго. Найти периметры этих квадратов.
б)Произведение двух последовательных натуральных чисел на 71 больше их суммы. Найдите эти числа.
Модуль «Геометрия»
16.Найдите координаты вершин треугольника МРК, образованного средними линиями треугольника АВС,
если А (—5; 1), В (3; —7), С ( -1; 3).
17. Найти периметр прямоугольника, если одна из его сторон равна 24, а диагональ равна 25.
Спецификация
контрольно—измерительных материалов для проведения
переводного экзамена в 8 классе в июне текущего учебного года учебного года
Спецификация составлена на основе Спецификации контрольно—измерительных материалов для проведения
в 2017 году основного государственного экзамена по математике, подготовленной ФГБНУ «Федеральный
институт педагогических измерений».
1. Назначение КИМ – оценить уровень общеобразовательной подготовки по математике учащихся 8
классов МКОУ «Парфеньевская СОШ» в целях подготовки к государственной итоговой аттестации
выпускников.
2. Характеристика структуры и содержания КИМ
Характеристика работы. Работа состоит из двух модулей: «Алгебра», «Геометрия». В модули
«Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровне
сложности.
Модуль «Алгебра» содержит 9 заданий: в части I – 6 заданий, в части II —3 задания повышенного
уровня сложности.
Модуль «Геометрия» содержит 8 заданий: в части I — 6 заданий, в части II — 2 задания
повышенного уровня сложности.
Всего в работе 17 заданий, из которых 12 заданий базового уровня (часть I), 5 заданий
повышенного уровня сложности (часть II).
Продолжительность работы – 150 минут.
Распределение заданий по уровням сложности
Уровень
сложности
(количество
баллов)
Планируемое
время на
выполнение (мин)
Критерии оценивания. Для заданий 1 части необходимо представить краткое решение и ответ, а
для заданий 2 части необходимо представить полное обоснованное решение и записать краткий ответ на
вопрос задачи. Задание из 1 части считается выполненным, если решение не содержит ошибок и получен
верный ответ Задание из 2 части считается выполненным, если решение не содержит ошибок и получен
верный ответ.
Баллы, полученные за верно выполненные задания, суммируются. Для получения
положительной отметки необходимо набрать не менее 5 баллов: 4 балла – «алгебра», 1 балл – «геометрия».
За каждое верно выполненное задание в части 1 и 2 выставляется 1 балл.
Критерии выставления оценок
Каждый пункт, отмеченный буквой а или б, считается как отдельное задание.
Оценка «3» ставится, если выполнено верно 5 заданий из первой части, при условии что одно задание из
модуля «Геометрия».
Оценка «4» ставится, если выполнено верно 7 заданий из первой части, при условии что 2 задания из
модуля «Геометрия» и 1 задание из второй части, любое.
Оценка «5» ставится, если выполнено верно 8 заданий из первой части, при условии что 2 задания из
модуля «Геометрия» и 2 задания из второй части, в том числе задание из модуля «Геометрия»
Распределение заданий КИМ по содержанию, проверяемым умениям и способам деятельности
Модуль «Алгебра»
Распределение заданий по частям работы
Максимальный
первичный балл
С кратким ответом в виде одной цифры,
которая соответствует номеру
правильного ответа
С кратким ответом в виде числа,
выражения , последовательности цифр
Распределение заданий части 1 по разделам содержательного курса математики
Распределение заданий части 1 по проверке умений и способностей
Уметь выполнять вычисления и преобразования
Уметь выполнять преобразования
алгебраических выражений
Уметь решать уравнения, неравенства и их
системы
Уметь строить и читать графики функций
Распределение заданий части 2 по разделам содержания курса математики
Название раздела содержания
Распределение заданий части 2 по проверяемым умениям и способам деятельности
Уметь выполнять вычисления и преобразования
Уметь выполнять преобразования алгебраических выражений
Решать текстовые задачи алгебраическим методом,
интерпретировать полученный результат, проводить отбор
решений исходя из формулировки задачи
Модуль «Геометрия»
Распределение заданий части 1 по разделам содержательного курса математики
Геометрические фигуры и их свойства
Распределение заданий части 1 по проверке умений и способностей
Уметь выполнять действия с геометрическими
фигурами
Проводить доказательные рассуждения при решении
задач, оценивать логическую правильность
рассуждений
Распределение заданий части 2 по разделам содержания курса математики
Название раздела содержания
Распределение заданий части 2 по проверяемым умениям и способам деятельности
Уметь выполнять действия с геометрическими
фигурами
Распределение заданий КИМ по уровню сложности
Уровень сложности заданий
Максимальный первичный
балл
Продолжительность контрольной работы
На выполнение работы отводится 150 минут.
Дополнительные материалы
Разрешается использовать линейку. Калькуляторы при выполнении работы не используются.
Обобщенный план варианта переводного экзамена в 8 классе
Уровень сложности заданий: Б — базовый, П – повышенный
Основные проверяемые требования к
математической подготовке
Уметь выполнять вычисления и преобразования,
уметь выполнять преобразования алгебраических
выражений
Уметь выполнять преобразования алгебраических
выражений
Основные проверяемые требования к
математической подготовке
Уметь выполнять вычисления и преобразования
Уметь решать уравнения, неравенства и системы
Уметь строить и читать графики
Уметь решать уравнения, неравенства и системы
Проводить доказательные рассуждения при решении
задач, оценивать логическую правильность
рассуждений, распознавать ошибочные заключения
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Уметь выполнять вычисления и преобразования
Уметь выполнять вычисления и преобразования,
уметь выполнять преобразования алгебраических
выражений
Решать текстовые задачи алгебраическим методом,
интерпретировать полученный результат, проводить
отбор решений исходя из формулировки задачи
Уметь выполнять действия с геометрическими
фигурами
Уметь выполнять действия с геометрическими
фигурами
Всего заданий — 17; из них заданий с кратким ответом –12, заданий с развернутым решением 5; Б—12, П—
5. Максимальный первичный балл -17.
Общее время выполнения работы –150 минут.
Кодификатор составлен на основе Кодификатора элементов содержания для проведения основного
государственного экзамена по математике, подготовленного ФГБНУ «Федеральный институт
педагогических измерений».
Код
контролируем
ого элемента
Элементы содержания, проверяемые заданиями переводного экзамена
Десятичная система счисления.
Обыкновенная дробь, основное свойство дроби. Сравнение дробей
Арифметические действия с десятичными дробями
Представление десятичных дробей в виде обыкновенных и наоборот
Квадратный корень из числа
Понятие об иррациональном числе. Десятичные приближения
иррациональных чисел
Сравнение действительных чисел
Измерения, приближения, оценки
Единицы измерения длины, площади, объема, массы, времени, скорости
Представление зависимости между величинами в виде формул
Буквенные выражения, выражения с переменными
Буквенные выражения. Числовые значения буквенного выражения
Подстановка выражений вместо переменных
Равенство буквенных выражений, тождество. Преобразование выражений
Многочлен. Сложение, вычитание, умножение многочленов
Разложение многочлена на множители
Алгебраическая дробь, сокращение дробей
Действия с алгебраическими дробями
Рациональные выражения и их преобразования
Свойства квадратных корней и их применение в вычислениях
Уравнения с одной переменной, корень уравнения
Квадратное уравнение, формула корней квадратного уравнения
Системы уравнений, решение системы
Решение текстовых задач алгебраическим способом
Линейная функция, ее график, геометрических смысл коэффициента
Геометрические фигуры и их свойства. Измерение геометрических величин
Начальные понятия геометрии
Прямоугольный треугольник. Теорема Пифагора
Зависимость между величинами сторон и углов треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника
Решение прямоугольных треугольников. Основное тригонометрическое
тождество. Теорема косинусов, теорема синусов
Операции над векторами (сумма векторов, умножение вектора на число)
Кодификатор требований к уровню подготовки обучающихся для проведения переводного экзамена
по математике в 8 классе. Июнь текущего учебного года
Кодификатор составлен на основе Кодификатора требований к уровню подготовки обучающихся
для проведения основного государственного экзамена по математике, подготовленного ФГБНУ
«Федеральный институт педагогических измерений».
Код
контролир
уемого
умения
Требования (умения), проверяемые заданиями работы
Уметь выполнять вычисления и преобразования
Выполнять арифметические действия с рациональными числами, сравнивать
действительные числа, переходить от одной формы записи числа к другой
Решать текстовые задачи, включая задачи, связанные с отношением,
пропорциональностью величин, дробями, процентами
Уметь выполнять преобразования алгебраических выражений
Составлять буквенные выражения и формулы по условиям задачи, находить
значения буквенных выражений, осуществляя необходимые подстановки и
преобразования
Выполнять основные действия со степенями с целыми показателями, с
многочленами и алгебраическими дробями
Выполнять разложение многочлена на множители
Выполнять тождественные преобразования рациональных выражений
Применять свойства арифметического квадратного корня для преобразования
числовых выражений, содержащих квадратные корни
Уметь решать уравнения, неравенства и их системы
Решать линейные, квадратные уравнения и рациональные, сводящиеся к ним,
системы двух линейных уравнений
Решать текстовые задачи алгебраическим способом
Уметь строить и читать графики функций
Определять свойства функции по ее графику
Строить графики функций, описывать их свойства
Уметь выполнять действия с геометрическими фигурами, координатами
и векторами
Решать планиметрические задачи на нахождение геометрических величин
(длин, углов)
Распознавать геометрические фигуры на плоскости, различать их взаимное
расположение, изображать геометрические фигуры, выполнять чертежи по
условию задачи
Уметь использовать приобретенные знания и умения в практической
деятельности и повседневной жизни. Уметь строить и исследовать
простейшие математические модели
Решать несложные практические расчетные задачи, связанные с отношением,
пропорциональностью величин, дробями, процентами, пользоваться оценкой
и прикидкой при практических расчетах, интерпретировать результаты
решения задач с учетом ограничений, связанных с реальными свойствами
рассматриваемых объектов
Моделировать реальные ситуации на языке алгебры, составлять уравнения,
неравенства по условию задачи, исследовать полученные модели с
использованием аппарата алгебры
Описывать с помощью функций различные реальные зависимости между
величинами, интерпретировать графики реальных зависимостей
Проводить доказательные рассуждения при решении задач, оценивать
логическую правильность рассуждений, распознавать ошибочные заключения