Решение и ответы заданий Варианта №1 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задания №13,16 долго оформлять, решу их позже, если будет время и желание.
Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
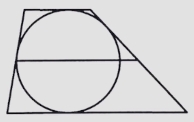
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Задание 2.
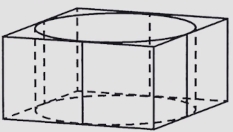
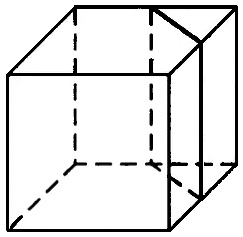
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Задание 3.
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Задание 4.
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Задание 5.
Найдите корень уравнения log3 (5 – 2x) = log3 (1 – 4x) + 1.
Задание 6.
Найдите значение выражения frac{sin126^{circ }}{4sin63^{circ }sin27^{circ }}.
Задание 7.
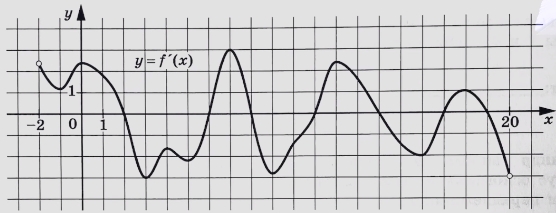
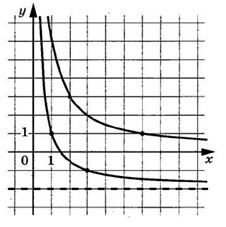
На рисунке изображён график y = f′(x) – производной функции f(x), определенной на интервале (−2; 20). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [1; 15].
Задание 8.
При адиабатическом процессе для идеального газа выполняется закон pVk = 1,3122·107 Па·м4, где p –давление в газе в паскалях, V – объём газа в кубических метрах, k = frac{4}{3}. Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 1,25·106 Па.
Задание 9.
Моторная лодка прошла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Задание 10.
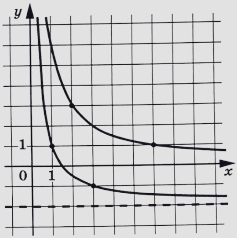
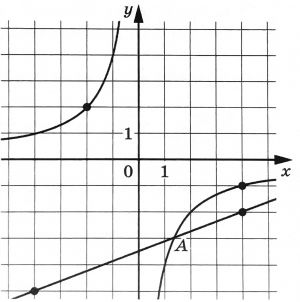
На рисунке изображены части графиков функций f(x)=frac{k}{x} и g(x)=frac{c}{x}+d. Найдите ординату точки пересечения графиков этих функций.
Задание 11.
Найдите наименьшее значение функции y = x√x − 27x + 6 на отрезке [1; 422].
Задание 12.
а) Решите уравнение 2sin2x – 3cos(–x) – 3 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [2pi;frac{7pi}{2}].
Задание 13.
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD = 9, BC = 7, SO = 6, а прямая SO перпендикулярна прямой AD.
Задание 14.
Решите неравенство 4^{x}+frac{112}{4^{x}–32}le 0.
Задание 15.
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2028 и 2029 годах должны быть равными;
– к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж в 2028 году?
Задание 16.
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE.
а) Докажите, что AL·AC = AB·ВC.
б) Найдите EL, если AC = 21, tg∠BCA = 0,4.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
(a – x)2 + 4a + 1 = (2x + 1)2 – 8|x|
имеет четыре различных корня.
Задание 18.
Есть три коробки: в первой коробке 112 камней, во второй – 99, в третья – пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй – 99, в третьей – 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.9 / 5. Количество оценок: 20
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30
Решение 36 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Острые углы прямоугольного треугольника равны 80° и 10°. Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 11. Найдите объём куба.
В сборнике билетов по философии всего 50 билетов, в 6 из них встречается вопрос по теме «Кант». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кант».
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов. Известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события «стрелок поразит ровно четыре мишени» больше вероятности события «стрелок поразит ровно три мишени»?
Найдите корень уравнения (log_{5}{(x+7)}=log_{5}(5-x)-1).
Найдите значение выражения (dfrac{20}{(2sqrt{2})^2}).
Прямая (y=6x+7) параллельна касательной к графику функции (y=x^2-5x+6). Найдите абсциссу точки касания.
При адиабатическом процессе для идеального газа выполняется закон (pV^k=7{,}776cdot10^6,Паcdotм^4), где (p) – давление в газе в паскалях, (V) – объём газа в кубических метрах, (k=dfrac{4}{3}). Найдите, какой объём (V) (в куб. м) будет занимать газ при давлении (p), равном (3,75cdot10^6,Па)
Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 53 часа после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках А и В. Найдите ординту точки В.
Найдите точку минимума функции (y=-dfrac{x}{x^2+900}).
а) Решите уравнение (4sin^4x+7cos^2x-4=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([-5pi; -4pi]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π | 18. -29π/6 | 19. -19π/4 | 20. -14π/3 |
| 21. -9π/2 | 22. -13π/3 | 23. -17π/4 | 24. -25π/6 |
| 25. -4π | 26. -23π/6 | 27. -15π/4 | 28. -11π/3 |
| 29. -7π/2 |
Основанием пирамиды (FABC) является правильный треугольник (ABC) со стороной (48). Все боковые рёбра пирамиды равны (40). На рёбрах (FB) и (FC) отмечены соответственно точки (K) и (N) так, что (FK=FN=10). Через точки (K) и (N) проведена плоскость (alpha), перпендикулярная плоскости (ABC).
а) Докажите, что плоскость (alpha) делит медиану (AM) в отношении (1:3).
б) Найдите расстояние от точки (C) до плоскости (alpha).
Решите неравенство (3log^2_{4}{(4-x)^8}+4log_{0{,}5}{(4-x)^6}geqslant72)
15 декабря планируется взять кредит в банке на сумму 1 000 000 рублей на (n+1) месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1 378 тысяч рублей.
В треугольнике (ABC) известно, что (AC=26) и (AB=BC=38).
а) Докажите, что средняя линия треугольника, параллельная стороне (AC), пересекает окружность, вписанную в треугольник (ABC).
б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне (AC).
Найдите все значения параметра (a), при каждом из которых любое значение из промежутка ([-1{,}5;-0{,}5]) является решением неравенства ((4|x|-a-3)(x^2-2x-2-a)geqslant0).
Группу детей можно перевезти автобусами модели А или автобусами модели Б. Известно, что в автобусе модели А количество мест больше 40, но меньше 50, а в автобусах модели Б — больше 50, но меньше 60. Если всех детей рассадить в автобусы модели А, то все места будут заняты. Если всех детей рассадить в автобусы модели Б, то все места также будут заняты, но потребуется на один автобус меньше.
а) Может ли потребоваться 4 автобуса модели Б?
б) Найдите наибольшее возможное количество детей в группе, если известно, что их меньше 300.
в) Найдите наибольшее возможное количество автобусов модели А.
Введите ответ в форме строки «да;123;1234». Где ответы на пункты разделены «;», и первый ответ с маленькой буквы.
Задание 1
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Скрыть
Задание 2
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Скрыть
Задание 3
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Скрыть
Задание 4
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Ответ: 0,89
Скрыть
Задание 5
Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$
Ответ: -0,2
Скрыть
Задание 6
Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$
Ответ: 0,5
Скрыть
Задание 7
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.
Ответ: 5
Скрыть
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.
Ответ: 5,832
Скрыть
Задание 9
Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Скрыть
Задание 10
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$
Ответ: -2910
Скрыть
Задание 12
а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$
Скрыть
Задание 13
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.
б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.
Ответ: 24
Скрыть
Задание 14
Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$
Ответ: $$(-infty;1];[log_{4} 28;2,5)$$
Скрыть
Задание 15
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— платежи в 2028 и 2029 годах должны быть равными;
— к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
Ответ: 400 тыс. руб.
Скрыть
Задание 16
В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.
а) Докажите, что $$AL:AC=AB:BC$$.
б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.
Ответ: 14,2
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.
Ответ: (-4;-3);(-3;-1);(-1;0)
Скрыть
Задание 18
Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Ответ: а)да б)нет в)195
Скрыть
Перейти к содержимому
ЕГЭ-2023. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике. В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с демоверсиями КИМ ЕГЭ 2023 года; ответы ко всем заданиям и критерии оценивания.
Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться:
Наверх
Скачать бесплатно сборник Ященко И.В. ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с ответами и решением.
Скачать сборник Ященко ЕГЭ 2023 в PDF
Аннотация к сборнику «ЕГЭ 2023. Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
Ященко ЕГЭ 2023 математика профиль 36 вариантов
В сборнике представлены: -36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2023 года; — инструкция по выполнению экзаменационной работы; — ответы ко всем заданиям; — решения и критерии оценивания заданий 12-18.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ. Под редакцией И. В. Ященко.
-
Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
-
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
| 3636 | Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106°, угол CAD равен 69°. Найдите угол ABD. Ответ дайте в градусах Решение |
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 1 |  |
| 3635 | В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=6, AA1=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1Решение |
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=6, AA1=5 ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 2 | |
| 3634 | Найдите значение выражения cos α, если иtg(alpha)=-sqrt(21)/2 и alpha in ((3pi)/2; 2pi)Решение |
Найдите значение выражения cos α, если tg α = — корень из 21 / 2 и α in (3 пи/2; 2пи) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 6 | |
| 3633 | На рисунке изображён график функции f(x)=k/(x+a). Найдите f(-7)
|
На рисунке изображён график функции f(x)=k / x+a Найдите f(-7) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 10 | |
| 3632 | Найдите точку максимума функции y= -(x^2+196)/xРешение  График |
Найдите точку максимума функции y= — x2 + 196 / x ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 11 | |
| 3631 | В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6sqrt3 и BP=4 Решение |
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 16 # Задача-аналог 2559 | |
| 3630 | Через концы A и B дуги окружности с центром O проведены касательные CA и CB. Угол CAB равен 39°. Найдите угол AOB. Ответ дайте в градусахРешение |
Через концы A и B дуги окружности с центром O проведены касательные CA и CB ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 1 | |
| 3629 | Объём параллелепипеда ABCDA1B1C1D1 равен 60. Найдите объём треугольной пирамиды ACB1D1Решение |
Объём параллелепипеда ABCDA1B1C1D1 равен 60. Найдите объём треугольной пирамиды ACB1D1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 2 | |
| 3628 | Найдите корень уравнения log_{0.5}(x+5)=log_{2}(0.2)Решение График |
Найдите корень уравнения log0,5 (x+5) = log2 0,2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 5 | |
| 3627 | Найдите значение выражения (14^6.4*7^-5.4)/4^2.2Решение |
Найдите значение выражения 14^6.4*7^-5.4 /4^2.2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 6 | |
Показать ещё…
Показана страница 1 из 24