Решебник егэ профильная математика 2022 ященко - Помощь в подготовке к экзаменам и поступлению

Решение и ответы заданий Варианта №1 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.

Задание 1.
Найдите корень уравнения 4^5х+2 = 0,8·5^5х+2.

Задание 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Задание 3.
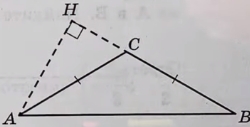
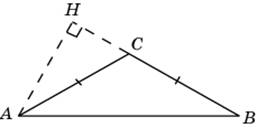
В тупоугольном треугольнике ABC известно, что AC = BC = 10, высота AH равна √51. Найдите косинус угла ACB.

Задание 4.
Найдите значение выражения frac{5sin61^{circ}}{sin299^{circ}}.

Задание 5.
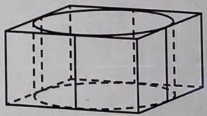
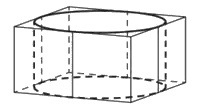
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Задание 6.
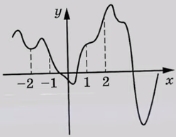
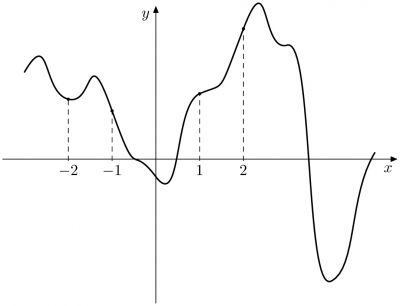
На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, –1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Задание 7.
При температуре 0°С рельс имеет длину l₀= 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(𝑡°) = l₀(1 + α∙t°), где α = 1,2∙10⁻⁵(°С )⁻¹ – коэффициент теплового расширения, t° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.

Задание 8.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно в А со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из B в А. Ответ дайте в км/ч.

Задание 9.
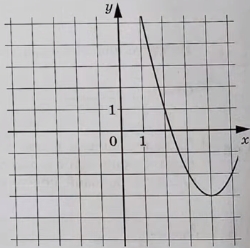
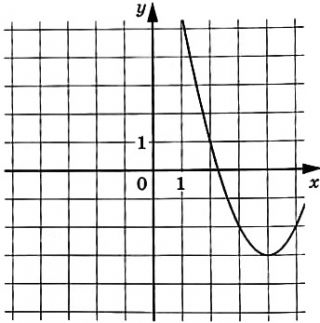
На рисунке изображён график функции вида f(x) = ax² + bx + c, где числа a, b и c – целые. Найдите значение f(−5).

Задание 10.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Задание 11.
Найдите наименьшее значение функции y = frac{4}{3}x√x – 3x + 9 на отрезке [0,25; 30].

Задание 12.
а) Решите уравнение 2sin³(π + x) = frac{1}{2}cos(x – frac{3pi }{2}).
б) Найдите все корни уравнения, принадлежащие отрезку [-frac{7pi }{2};-frac{5pi }{2}].

Задание 13.
Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА. Плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно.

а) Докажите, что площадь четырёхугольника BCPQ составляет frac{3}{4} площади треугольника SBC
б) Найдите объем пирамиды KBCPQ.

Задание 14.
Решите неравенство (4^х – 5·2^х)² – 20(4^х – 5·2^х) ≤ 96.

Задание 15.
В июле 2025 года планируется взять кредит на 8 лет. Условия его возврата таковы:
– в январе 2026, 2027, 2028, 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года;
– в январе 2030, 2031, 2032, 2033 годов долг возрастает на 18% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат до полного его погашения составит 1125 тысяч рублей?

Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.

а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD = 6, АЕ = √6.

Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение

|x^{2}-a^{2}|=|a+x|cdot sqrt{x^{2}-4ax+5a}

имеет ровно один корень.

Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.

а) Может ли сумма этих чисел быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.1 / 5. Количество оценок: 17

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

ЕГЭ 2022, полный разбор 36 варианта Ященко ФИПИ школе 36 вариантов. Решаем типовые варианты от Ященко 2022 года ЕГЭ профиль!

Решаем 36 вариант Ященко 2022 года сборника ФИПИ школе 36 вариантов. Разбор 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 задания.

Больше разборов на моем ютуб-канале

Задание 1

Найдите корень уравнения $$sqrt{frac{6}{4x-54}}=frac{1}{7}.$$

Ответ: 87

Скрыть

$$(sqrt{frac{6}{4x-54}})^2=(frac{1}{7})^2$$

$$frac{6}{4x-54}=frac{1}{49}$$

$$4x – 54 = 294$$

$$4x = 294 + 54$$

$$4x = 348$$

$$x = 87$$

Задание 2

На рок-фестивале выступают группы — по одной от каждой из заявленных стран, в том числе группы из Италии, Германии, Австрии и Испании. Порядок выступления определяется жребием. Какова вероятность того, что группа из Германии будет выступать позже групп из Италии, Австрии и Испании? Ответ округлите до сотых.

Ответ: 0,25

Скрыть

Если поставить Германию после трех групп, то количество перестановок без повторений из этих 3 групп (Италии, Австрии и Испании) будет равно 3! . Заметим, что это благоприятствующие исходы m.

А общее количество перестановок из всех 4 групп равно 4! это n.

Таким образом, вероятность того, что группа из Германии будет выступать позже групп из Италии, Австрии и Испании будет равна

$$P(A)=frac{3!}{4!}=frac{1cdot2cdot3}{1cdot2cdot3cdot4}=frac{1}{4}=0,25$$

Задание 3

Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Ответ: 17

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4

Найдите значение выражения: $$3^{2+log_{3}7}$$

Ответ: 63

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5

В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые рёбра призмы равны $$frac{4}{pi}$$. Найдите объём цилиндра, описанного около этой призмы.

Ответ: 61

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6

Прямая $$y=-5x+6$$ является касательной к графику функции $$28x^2+23x+c$$. Найдите с.

Ответ: 13

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7

Груз массой 0,58 кг колеблется на пружине. Его скорость $$v$$ (в м/с) меняется по закону $$v=v_{0}sin frac{2pi t}{T}$$, где t — время с момента начала колебаний в секундах, Т=6 с — период колебаний, $$v_{0}$$=2 м/с. Кинетическая энергия Е (в Дж) груза вычисляется по формуле $$E=frac{mv^{2}}{2}$$, где m — масса груза (в кг), $$v$$ — скорость груза (в м/с). Найдите кинетическую энергию груза через 4 секунды после начала колебаний. Ответ дайте в джоулях.

Ответ: 0,87

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8

Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 21 час. Через 5 часов после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Ответ: 13

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9

На рисунке изображена часть графика функции $$f(x)=|kx+b|.$$ Найдите $$f(-15).$$

Ответ: 1,2

Скрыть

$$f(x)$$ проходит через $$(-2;4)$$ и $$(-7;2).$$

При этом изображено «положительное» раскрытие модуля, т. е. $$f(x)=kx+b,kgeq0.$$

Получим:

$$left{begin{matrix} 4=-2k+b\ 2=-7k+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=0,4\ b=4,8 end{matrix}right.$$

Получим:

$$f(x)=|0,4x+4,8|, тогда: f(-15)=|0,4cdot(-15)+4,8|=|-1,2|=1,2.$$

Задание 10

В викторине участвуют 15 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых 8 играх победила команда А. Какова вероятность того, что эта команда выиграет девятый раунд?

Ответ: 0,9

Скрыть

Если команда «А» выиграла n раундов, то вероятность, что команда «А» выиграет в n+1 раунде:

$$1-frac{1}{n+2}$$

Тогда:

$$1-frac{1}{8+2}=1-frac{1}{10}=1-0,1=0,9$$

Задание 11

Найдите наименьшее значение функции $$y=6+frac{sqrt{3}pi}{2}-3sqrt{3}x-6sqrt{3}cos x$$ на отрезке $$[0;frac{pi}{2}]$$

Ответ: -3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12

а) Решите уравнение: $$cos 4x-sin 2x=0$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0;pi]$$

Ответ: а)$$frac{pi}{12}+frac{pi k}{3}, kin Z$$ б)$$frac{pi}{12};frac{5pi}{12};frac{3pi}{4}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13

В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G — середина ребра SC.

а) Постройте прямую пересечения плоскостей ABG и GDF.

б) Найдите угол между плоскостями ABG и GDF.

Ответ: $$arccos frac{9}{11}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14

Решите неравенство: $$9^{x}-10cdot 3^{x+1}+81geq 0$$

Ответ: $$(-infty;1]cup[3;+infty)$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15

31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2 928 200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?

Ответ: 9 282 000 рублей

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16

Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE.

а) Докажите, что четырёхугольник BCFE — параллелограмм.

б) Найдите площадь четырёхугольника ABCD, если известно, что АВ=6 и АН=$$2sqrt{5}$$.

Ответ: $$48+18sqrt{5}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 17

Найдите все значения а, при каждом из которых функция

$$f(x)=x^{2}-4|x-a^{2}|-8x$$

имеет хотя бы одну точку максимума.

Ответ: $$ain(-sqrt{6};-sqrt{2})cup(sqrt{2};sqrt{6})$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18

Имеется 8 карточек. На них записывают по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 1?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

Ответ: нет; нет; 16

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Источник


3577	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD Решение	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525

3334	В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, точка G — середина ребра SC. а) Постройте прямую пересечения плоскостей ABG и GDF. б) Найдите угол между плоскостями ABG и GBF Решение	а) Постройте прямую пересечения плоскостей ABG и GDF ! 36 вариантов ФИПИ Ященко 2022 Вариант 36 Задание 13

3309	Найдите наибольшее значение функции y=ln((x+9)^5)-5x на отрезке [-8,5; 0] Решение График	Найдите наибольшее значение функции y= ln(x+9)5 -5x на отрезке [-8,5; 0] ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 11

3308	а) Решите уравнение ((0.25)^sin(x))^cos(x)=2^(-sqrt(2)sin(x)) б) Найдите все корни этого уравнения, принадлежащие промежутку [2pi; (7pi)/2]. Решение График	а) Решите уравнение ((0,25) sinx) cosx = 2 -sqrt2 sinx ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 12

3307	На рисунке изображён график функций f(x)=(kx+a)/(x+b). Найдите k Решение	На рисунке изображён график функций f(x)= kx+a / (x+b). Найдите k ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 9

3306	На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точках A(x0; y0) и B(4; 5). Найдите y0 Решение График	На рисунке изображены графики функций, которые пересекаются в точках A(x0; y0) и B(4; 5) ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 9

3305	Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 75 % кислоты. Сколько процентов кислоты содержится в первом сосуде? Решение	Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 8

3304	На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точке A. Найдите абсциссу точки A Решение График	На рисунке изображены графики функций. Найдите абсциссу точки A ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 9

3303	За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки. Найдите вероятность того, что рядом с любым мальчиком будут сидеть две девочки Решение	За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 10

3302	В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зелёных, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зелёных, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета Решение	Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета ! 36 вариантов ФИПИ Ященко 2022 Вариант 30 Задание 10

Показана страница 1 из 27

Источник

Перейти к содержимому

И.В. Ященко, И.Р. Высоцкий, Е. А. Коновалов ЕГЭ-2022. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике. В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ 2022 года; ответы ко всем заданиям и критерии оценивания.

Читать онлайн и скачать сборник в формате PDF: Скачать

* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы

Источник

Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».

Вариант 1

1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910

Вариант 2

1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25

Вариант 3

1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204

Вариант 4

1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9

Вариант 5

1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52

Вариант 6

1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6

Вариант 7

1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5

Вариант 8

1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17

Вариант 9

1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9

Вариант 10

1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25

Вариант 11

1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75

Вариант 12

1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25

Вариант 13

1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77

Вариант 14

1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37

Вариант 15

1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208

Вариант 16

1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5

Вариант 17

1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24

Вариант 18

1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15

Вариант 19

1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34

Вариант 20

1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0

Вариант 21

1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7

Вариант 22

1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2

Вариант 23

1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18

Вариант 24

1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2

Вариант 25

1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14

Вариант 26

1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1

Вариант 27

1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3

Вариант 28

1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38

Вариант 29

1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21

Вариант 30

1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8

Вариант 31

1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8

Вариант 32

1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9

Вариант 33

1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26

Вариант 34

1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1

Вариант 35

1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9

Вариант 36

1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30

Источник

Найдите корень уравнения (4^{5x+2}=0{,}8cdot 5^{5x+2})

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

В тупоугольном треугольнике ABC известно, что AC=BC=10, высота AH равна √51. Найдите косинус угла ACB.

Найдите значение выражения (dfrac{5sin61°}{sin299°})

Цилиндр вписан в правильную четырехугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

На рисунке изображен график (y=f(x)). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

При температуре (0°C) рельс имеет длину (l_0 = 10)м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону (l(t°) = l_0(1 + a ⋅ t°)), где (a = 1{,}2cdot 10^{-5}(°C)^{-1}) – коэффициент теплового расширения, (t°) – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.

На рисунке изображен график функции (f(x)=ax^2+bx+c), где числа (a), (b) и (c) – целые. Найдите (f(-5)).

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая — 70%. Среди стекол, выпущенных на первой фабрике, 5% бракованные, а на второй — 4% бракованные. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Найдите наименьшее знаение функции (y=dfrac43xsqrt{x}-3x+9) на отрезке ([0{,}25;30])

а) Решите уранение (2sin^3(pi+x)=dfrac12cosleft(x-dfrac{3pi}{2}right))
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{7pi}2;-dfrac{5pi}2right])

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.

а)

1. 2πn, n∈Z	2. π/6+2πn, n∈Z	3. π/4+2πn, n∈Z	4. π/3+2πn, n∈Z
5. π/2+2πn, n∈Z	6. 2π/3+2πn, n∈Z	7. 3π/4+2πn, n∈Z	8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z	10. -π/6+2πn, n∈Z	11. -π/4+2πn, n∈Z	12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z	14. -2π/3+2πn, n∈Z	15. -3π/4+2πn, n∈Z	16. -5π/6+2πn, n∈Z

б)

17. -7π/2	18. -10π/3	19. -13π/4	20. -19π/6
21. -3π	22. -17π/6	23. -11π/4	24. -8π/3
25. -5π/2

В правильной треугольной пирамиде SABC сторона основания AB равна 16, высота SH равна 10. Точка K – середина бокового ребра SA. Плоскость, параллельная плоскости ABC, проходит через точку K и пересекает рёбра SB и SC в точках Q и P соответственно.
а) Докажите, что площадь четырехугольника BCPQ составляет 3/4 площади треугольника SBC.
б) Найдите объем пирамиды KBCPQ.

Решите неравенство ((4^x-5cdot 2^x)^2-20(4^x-5cdot2^x)leqslant96)

В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы:
– в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года;
– в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, сели общая сумма выплат после полного его погашения составит 1125 тысяч рублей?

Точки A, B, C, D и E лежат на окружности в указанном порядке, причём AE=ED=CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.
а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD=6, AE=√6.

Найдите все значения параметра (a), при каждом из которых уравнение (|x^2-a^2|=|x+a|cdotsqrt{x^2-4ax+5a}) имеет ровно один корень.

На доске написано три различных натуральных числа. Второе число равно сумме цифр первого, а третье сумме цифр второго.
а) Может ли сумма этих числ быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Источник

Математика ЕГЭ
Математика ОГЭ
Биология ОГЭ
Биология ЕГЭ
Физика ОГЭ
Физика ЕГЭ
Химия ЕГЭ
Химия ОГЭ
Русский язык ОГЭ
Русский язык ЕГЭ
Английский язык ОГЭ
Английский язык ЕГЭ
Литература ЕГЭ
Литература ОГЭ
История ЕГЭ
История ОГЭ
Информатика ЕГЭ
Информатика ОГЭ
География ЕГЭ
География ОГЭ

Вы здесь: ✔️ Главная сайта ГДЗ Математика ЕГЭ Ященко ЕГЭ-2022 36 вариантов профильный уровень математика

👀 Просмотров: 5773

Инфо

Автор: И.В. Ященко

Предмет (категория): Профильный уровень. 36 вариантов заданий

Класс:

Читать онлайн: Да

Скачать бесплатно: Да

Формат книги: jpg / pdf

Размер книги/ГДЗ: 25,8 Мб

Год публикации (выпуска): 2022

Читать онлайн или скачать 36 вариантов для подготовки к Единому государственному экзамену по математике под редакцией Ященко 2022 года:

Самые популярные статьи:

ЕГЭ 2015. Ященко Математика. 36 вариантов.
Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика

Вперёд >

Вам это пригодится

Барашкова английский язык на каникулах н…