Задание 1
Призёрами городской олимпиады по математике стали 20 учеников, что составило 10 % от числа участников. Сколько человек участвовало в олимпиаде?
Ответ: 200
Скрыть
Для определения исходного числа участников, нужно 20 разделить на коэффициент 10/100 , получим: 20:0,1 = 200 участников.
Задание 2
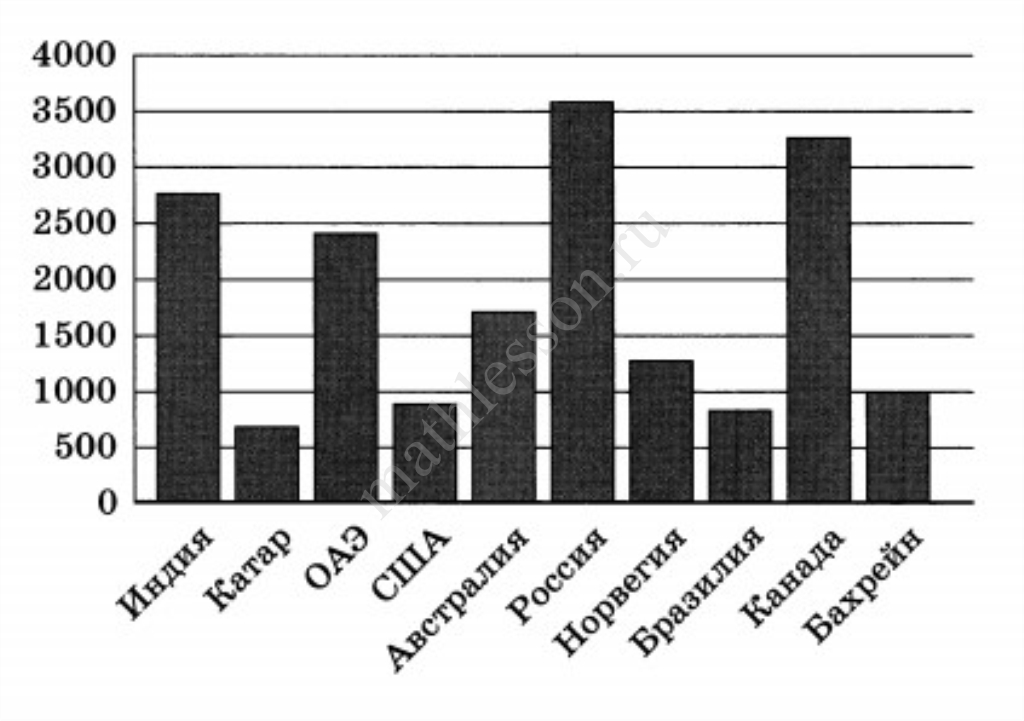
На диаграмме показано распределение выплавки алюминия в 10 странах мира (в тысячах тонн) за 2016 год. Среди представленных стран первое место по выплавке алюминия занимала Россия, десятое место занимал Катар. Какое место занимала Норвегия?
Ответ: 6
Скрыть
Больше у Индии, ОАЭ, Австралии, России и Канады. Следовательно, 6 место
Задание 3
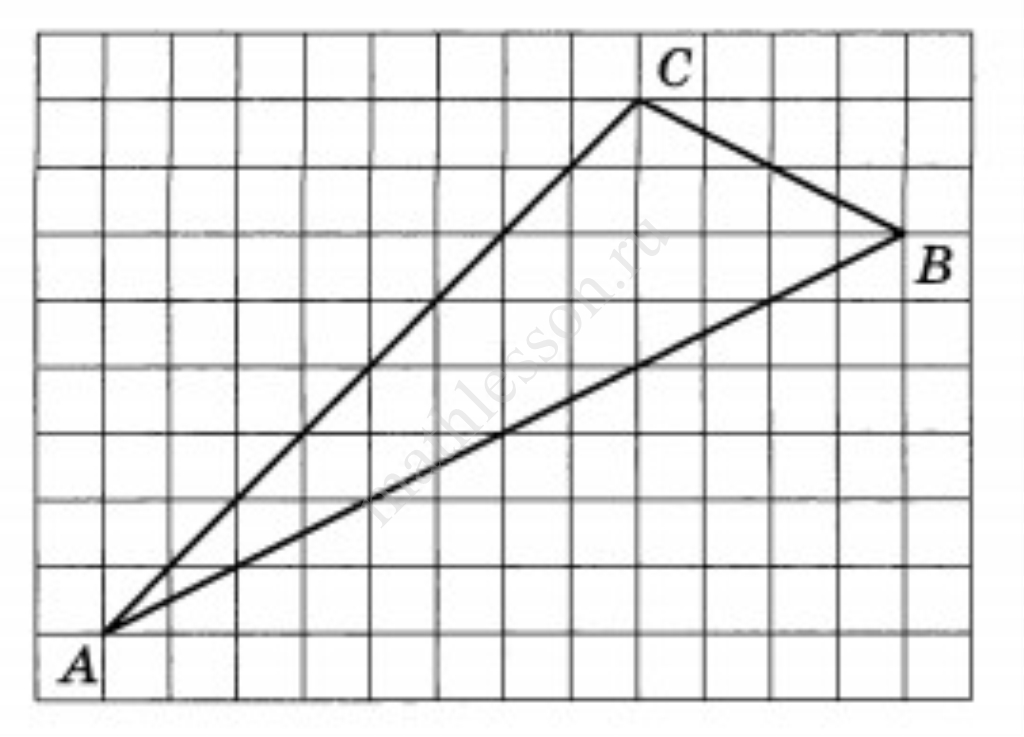
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его биссектрисы, проведённой из вершины В.
Ответ: 6
Скрыть
Угол С — прямой, его биссектриса пойдет по сторонам клетки и составит по длине 4 клетки.
Задание 4
За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2 девочки. Найдите вероятность того, что девочки окажутся на соседних местах.
Ответ: 0,2
Скрыть
Допустим, первая девочка уже села на какое-то место. Вероятность этого события 1. Осталось 11-1=10 мест. Чтобы вторая девочка оказалась рядом с первой, она может сесть либо слева, либо справа от нее. Получаем число благоприятных исходов m=2. Учитывая, что всех возможных исходов n=10, получаем значение искомой вероятности:
$$P=frac{m}{n}=frac{2}{10}=0,2$$
Задание 5
Найдите корень уравнения $${left(x — 4right)}^3 = 729$$
Ответ: 13
Скрыть
$$(x-4)^{3}=729Leftrightarrow$$$$x-4=sqrt[3]{729}Leftrightarrow$$$$x=9+4=13$$
Задание 6
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 72$${}^circ$$, угол CAD равен 58$${}^circ$$. Найдите угол АВС. Ответ дайте в градусах.
Ответ: 130
Скрыть
Угол ∠АВD = 72° – вписанный в окружность угол. Вписанный в окружность угол измеряется половиной дуги, на которую он опирается, следовательно, дуга АD = 144°.
Угол ∠CAD = 58° – вписанный в окружность угол, следовательно, дуга CD = 116°.
Дуга AC = AD + DC AC = AD + DC = 144° + 116° = 260°
Угол ∠ABC – вписанный в окружность угол, который опирается на дугу АС, следовательно, ∠AВС = 130°.
Задание 7
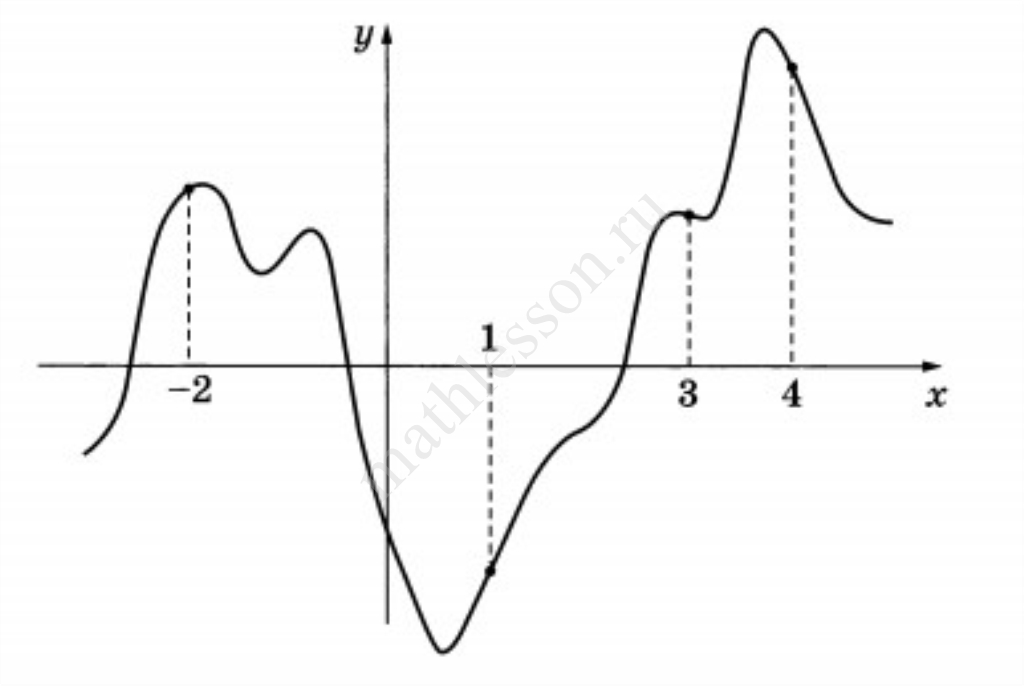
На рисунке изображён график функции $$y = f(x).$$ На оси абсцисс отмечены точки -2, 1, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: 1
Скрыть
1. Значение производной положительно в некоторой точке x, если в окрестности этой точки функция возрастает. Наоборот, если в окрестности точки x функция убывает, то производная в ней отрицательна. Причем значение производной тем больше, чем сильнее изменение функции в окрестности точки x.
2. Выберем точку на графике, в которой функция возрастает наибольшим образом. Это точка 1.
Задание 8
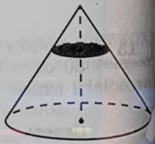
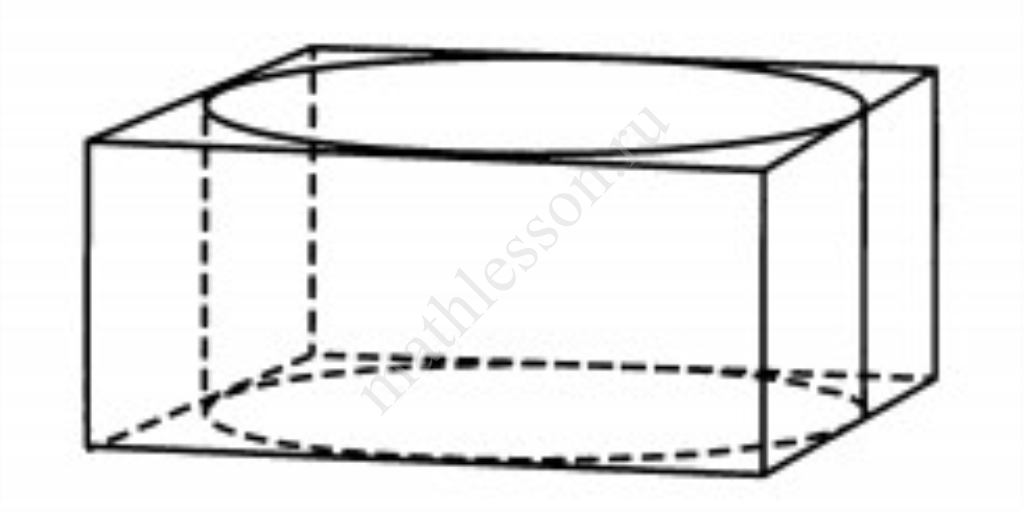
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 7. Найдите объём параллелепипеда.
Ответ: 1372
Скрыть
Объем прямоугольного параллелепипеда равен: V = a·b·c Так как прямоугольный параллелепипед описан около цилиндра, то
a = b = 2R = 2·7 = 14
c = h = 7
V = 14·14·7 = 1372
Задание 9
Найдите значение выражения $$2sqrt{3}{{cos }^{{rm 2}} frac{17pi }{12} }-2sqrt{3}{{sin }^{{rm 2}} frac{17pi }{12} }$$
Ответ: -3
Скрыть
$$2sqrt{3}{{cos }^{{rm 2}} frac{17pi }{12} }-2sqrt{3}{{sin }^{{rm 2}} frac{17pi }{12} }=$$$$2sqrt{3}(cos^{2}frac{17pi}{12}-sin^{2}frac{17pi}{12})=$$$$2sqrt{3}cos frac{17pi}{6}=$$$$2sqrt{3}cos frac{5pi}{6}=$$$$2sqrt{3}cdot (-frac{sqrt{3}}{2})=-3$$
Задание 10
В ходе распада радиоактивного изотопа его масса уменьшается по закону $$m=m_0cdot 2^{-frac{t}{T}}$$, где $$m_0$$ — начальная масса изотопа, t — время, прошедшее от начального момента, Т — период полураспада. В начальный момент времени масса изотопа 52 мг. Период его полураспада составляет 9 мин. Найдите, через сколько минут масса изотопа будет равна 13 мг.
Ответ: 18
Скрыть
Задача сводится к решению неравенства m(t) больше или равно 13 при заданных значениях параметров $$m_{0}=52$$ мг и T=9 мин:
$$52cdot 2^{-frac{t}{9}}geq 13Leftrightarrow$$$$2^{frac{t}{9}}geq frac{1}{4}Leftrightarrow$$$$-frac{t}{9}geq -2Leftrightarrow$$$$tleq 18$$
Таким образом, масса радиоактивного изотопа будет не меньше 13 мг в течение 18 минут.
Задание 11
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч. Ответ дайте в км/ч.
Ответ: 1
Скрыть
Обозначим через x км/ч скорость течения. Тогда при движении ложки против течения, ее скорость была равна 12-x км/ч и на преодоления 143 км было потрачено $$frac{143}{12-x}$$ часов. При обратном движении лодка шла по течению, то есть ее скорость была равна 12+x км/ч и на преодоления 112 км было затрачено $$frac{143}{12+x}$$ часов. Известно, что на обратный путь было потрачено на 2 часов меньше. Имеем уравнение:
$$frac{143}{12-x}+frac{143}{12+x}=2$$
$$143(12+x)+143(12-x)=2(144-x^{2})$$
$$2x^{2}+286x-288=0$$
$$x^{2}+143x-144=0$$
Решаем квадратное уравнение получаем два корня:
$$x_{1}=1; x_{2}<0$$
Получаем один положительный корень x=3 км/ч.
Задание 12
Найдите точку минимума функции $$y = left(2x^2 — 26x + 26right)e^{x-17}.$$
Ответ: 11
Скрыть
1. Вычислим производную функции, получим: $$y’=(4x-26)e^{x-17}+(2x^{2}-26x+26)e^{x-17}=$$$$e^{x-17}(2x^{2}-22x)$$
2. Приравняем производную нулю и найдем точки экстремума функции: $$e^{x-17}(2x^{2}-22x)=0Leftrightarrow$$$$$$
так как $$e^{x-17}>0, xin R$$, то $$x_{1}=0, x_{2}=11$$
3. Точкой минимума будет являться та точка экстремума, в окрестности которой производная меняет свой знак с «-» на «+». Получаем точку $$x = 11$$.
Задание 13
а) Решите уравнение $$2sin^2x + cosx-1 = 0.$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-5pi ; -4pi ]$$
Ответ: а) $$frac{2pi k}{3}, k in Z$$; б) $$-frac{14pi }{3}; -4pi $$
Задание 14
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а $$AB = BC =AC = 10.$$
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки М и N соответственно, причём $$DM : MA = DN : NC = 3:2. $$Найдите площадь сечения MNB.
Ответ: $$3sqrt{59}$$
Задание 15
Решите неравенство $$frac{3}{{left(2^{2-x^2}-1right)}^2}-frac{4}{2^{2-x^2}-1}+1ge 0$$
Ответ: $$(-infty ; -sqrt{2}); (-sqrt{2}; -1]; 0; [1; sqrt{2}); (sqrt{2}; +infty )$$
Задание 16
Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках $$C_1,B_1,A_1$$ соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника $${AB}_1C_1$$
а) Докажите, что $$C_1Q$$ — биссектриса угла $$AC_1B_1$$
б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник $$AB_1C_1$$, если известно, что $$BC = 7, AB = 15, AC = 20.$$
Ответ: 2
Задание 17
В июле 2022 года планируется взять кредит в банке на сумму 427 000 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 25 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года)?
Ответ: 656250
Задание 18
Найдите все значения а, при каждом из которых уравнение $$(9x-4){ln (x+a) } = (9x-4){ln (2x+a) }$$ имеет ровно один корень на отрезке [0; 1].
Ответ: $$-frac{4}{9}<aleq 0; a=frac{2}{9}; frac{1}{2}<a<frac{8}{9}$$
Задание 19
Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1131 фотографий больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 13 дней?
б) Могли ли они фотографировать в течение 12 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 35 фотографий?
Ответ: а) да; б) нет; в) 1711
- 31.10.2020
Сборник ответов для пособия ЕГЭ 2021, 36 типовых вариантов по математике профильного уровня, под редакцией Ященко И.В.
- Тренировочные варианты ЕГЭ 2021 по математике
- Реальные варианты ЕГЭ 2020 по математике
- Работы СтатГрад 2020-2021
Выбирайте вариант и смотрите ответы по PDF файлу. Вы можете скачать их совершенно бесплатно.
Видеоразбор варианта №7 из сборника Ященко
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Видеоразбор варианта №5, Ященко
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
| 3631 | В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6sqrt3 и BP=4 |
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 16 # Задача-аналог 2559 | |
| 3577 | В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD |
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525 | |
| 3244 | В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt3. На ребрах C1D1 и DD1 отмечены соответственно точки K и M так, что D1K=KC1, а DM:MD1=1:3. а) Докажите, что прямые MK и BK перпендикулярны. б) Найдите угол между плоскостями BMK и ABB1 |
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt 3 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 13 # Задача-аналог 2574 | |
| 2881 | Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P. а) Докажите, что /_POA=/_PAO. б) Найдите площадь треугольника APO, если радиус описанной около треугольника ABC окружности равен 6, /_BAC=75^@, /_ABC=60^@ |
Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 16 # Задача-аналог 2623 | |
| 2877 | В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7. На рёбрах AB и SC отмечены точки K и M соответственно, причем AK:KB=SM:MC=1:5. Плоскость alpha содержит прямую KM и параллельна прямой BC. a) Докажите, что плоскость alpha параллельна прямой SA. б) Найдите угол между плоскостями alpha и SBC |
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7 ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 14 # Задача-аналог 1669 | |
| 2874 | Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1). а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 9 нулями? б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 23 нулями? в) Сколько существует натуральных чисел n, меньших 100, для каждого из которых десятичная запись числа n∙ (100 — n)! оканчивается ровно 23 нулями |
Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1) ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 19 | |
| 2873 | Найдите, при каких неотрицательных значениях a функция f(x)=3ax^4-8x^3 +3x^2-7 на отрезке [-1; 1] имеет ровно одну точку минимума |
Найдите, при каких неотрицательных значениях a функция f(x) на отрезке [-1; 1] имеет ровно одну точку минимума ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 17 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 18 | |
| 2872 | Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? |
Александр хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 15 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 17 | |
| 2853 | а) Решите уравнение 2sin^2(x)+cos(x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-5pi; -4pi]. |
а) Решите уравнение 2sin2 x + cosx -1 = 0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 36 Задание 13 | |
| 2852 | За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того, что девочки не окажутся на соседних местах |
За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 35 Задание 4 | |

Показана страница 1 из 21
|
Ответы и решения ЕГЭ-2021. Математика. 36 вариантов. Ященко |
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
Решение и ответы заданий варианта №1 из сборника ЕГЭ 2021 по математике (базовый уровень) И.В. Ященко. ГДЗ база для 11 класса.
Задание 1.
Найдите значение выражения
Задание 2.
Найдите значение выражения
Задание 3.
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 180 человек. Голоса между кандидатами распределились в отношении 2:3. Сколько голосов получил победитель?
Задание 5.
Найдите значение выражения
Задание 6.
Стоимость проездного билета на месяц составляет 655 рублей, а стоимость билета на одну поездку – 25 рублей. Аня купила проездной и сделала за месяц 47 поездок. На сколько рублей больше она бы потратила, если бы каждый раз покупала билет на одну поездку?
Задание 7.
Найдите корень уравнения 4 – 3(5 – 2х) = 9х – 2.
Задание 8.
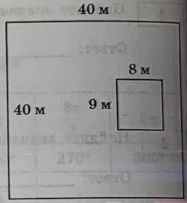
Дачный участок имеет форму квадрата, стороны которого равны 40 м. Дом, расположенный на участке имеет на плане форму прямоугольника, стороны которого равны 9 м и 8 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
Задание 9.
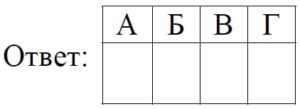
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ ЗНАЧЕНИЯ
А) площадь футбольного поля 1) 20 кв. м
Б) площадь жилой комнаты 2) 31 500 кв. км
В) площадь озера Байкал 3) 624 кв. см
Г) площадь листа писчей бумаги 4) 7000 кв. м
В таблице под каждой буквой, соответствующей величине, укажите номер ее возможного значения.
Задание 10.
На соревнованиях по прыжкам в воду участвуют 25 спортсменов, среди них 7 прыгунов из Канады. Порядок старта определяется случайным образом с помощью жребия. Известно, что третьим по порядку прыгает спортсмен из Канады. Найдите вероятность того, что вторым будет прыгать тоже представитель Канады.
Задание 11.
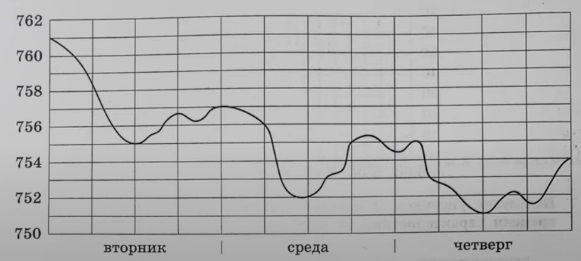
На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали – значения атмосферного давления в миллиметрах ртутного столба.
Определите по рисунку наибольшее значение атмосферного давления (в миллиметрах ртутного столба) в среду.
Задание 12.
Интернет-провайдер предлагает три тарифных плана.
Пользователь предполагает, что его трафик составит 700 Мб в месяц, и, исходя из этого, выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить пользователь за месяц, если его трафик действительно будет равен 700 Мб?
Задание 13.
Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см х 30 см х 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
Задание 14.
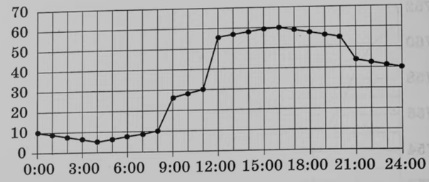
На рисунке точками показано потребление воды городской ТЭЦ на протяжении суток. По горизонтали указывается время, по вертикали – объём воды в кубометрах в час. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику потребления воды данной ТЭЦ в течение этого периода.
ПЕРИОДЫ ВРЕМЕНИ ХАРАКТЕРИСТИКИ
А) ночь (с 0 до 6 часов) 1) потребление воды достигло максимума за сутки
Б) утро (с 6 до 12 часов) 2) потребление воды падало в течение всего периода
В) день (с 12 до 18 часов) 3) потребление воды сначала падало, а потом росло
Г) вечер (с 18 до 24 часов) 4) наибольший рост потребления воды за сутки
В таблице под каждой буквой укажите соответствующий номер.
Задание 15.
Стороны параллелограмма равны 22 и 44. Высота, опущенная на меньшую сторону, равна 33. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 16.
Объём конуса равен 256. Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Задание 17.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце.
Установите соответствие между неравенствами и их решениями. Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.
Задание 18.
Когда учитель физики Николай Дмитриевич ведёт урок, он обязательно отключает свой телефон. Выберите утверждения, которые верны при приведённом условии.
1) Если телефон Николая Дмитриевича включён, значит, он не ведёт урок.
2) Если телефон Николая Дмитриевича включён, значит, он ведёт урок.
3) Если Николай Дмитриевич проводит на уроке лабораторную работу по физике, значит, его телефон выключен.
4) Если Николай Дмитриевич ведёт урок физики, значит, его телефон включён.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 19.
Найдите пятизначное число, кратное 15, любые дне соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
Задание 20.
Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 7 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Источник варианта: Сборник ЕГЭ 2021 по математике базовый уровень. Типовые экзаменационные варианты. 30 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30
Варианты Ященко ОГЭ: разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко ОГЭ 2020 года, а также разборы вариантов 2021 и 2022 годов.
Видео разборы вариантов ОГЭ-2022 из сборника Ященко (скачать сборник «36 вариантов» 2022 г.):
01
02
03 и 04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Видео разборы вариантов ОГЭ-2021 из сборника Ященко (скачать сборник «36 вариантов» 2021 г.):
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
Видео разборы всех вариантов ОГЭ-2020 из сборника Ященко (скачать сборник «36 вариантов» 2020 г.):
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36




 Скачать учебник и сборник ЕГЭ-2021. Математика Ященко И.В. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов. ФИПИ
Скачать учебник и сборник ЕГЭ-2021. Математика Ященко И.В. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов. ФИПИ