Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
ЕГЭ 2022, полный разбор 36 варианта Ященко ФИПИ школе 36 вариантов. Решаем типовые варианты от Ященко 2022 года ЕГЭ профиль!
Решаем 36 вариант Ященко 2022 года сборника ФИПИ школе 36 вариантов. Разбор 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 задания.
Больше разборов на моем ютуб-канале
Задание 1
Найдите корень уравнения $$sqrt{frac{6}{4x-54}}=frac{1}{7}.$$
Ответ: 87
Скрыть
$$(sqrt{frac{6}{4x-54}})^2=(frac{1}{7})^2$$
$$frac{6}{4x-54}=frac{1}{49}$$
$$4x – 54 = 294$$
$$4x = 294 + 54$$
$$4x = 348$$
$$x = 87$$
Задание 2
На рок-фестивале выступают группы — по одной от каждой из заявленных стран, в том числе группы из Италии, Германии, Австрии и Испании. Порядок выступления определяется жребием. Какова вероятность того, что группа из Германии будет выступать позже групп из Италии, Австрии и Испании? Ответ округлите до сотых.
Ответ: 0,25
Скрыть
Если поставить Германию после трех групп, то количество перестановок без повторений из этих 3 групп (Италии, Австрии и Испании) будет равно 3! . Заметим, что это благоприятствующие исходы m.
А общее количество перестановок из всех 4 групп равно 4! это n.
Таким образом, вероятность того, что группа из Германии будет выступать позже групп из Италии, Австрии и Испании будет равна
$$P(A)=frac{3!}{4!}=frac{1cdot2cdot3}{1cdot2cdot3cdot4}=frac{1}{4}=0,25$$
Задание 3
Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Ответ: 17
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Найдите значение выражения: $$3^{2+log_{3}7}$$
Ответ: 63
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые рёбра призмы равны $$frac{4}{pi}$$. Найдите объём цилиндра, описанного около этой призмы.
Ответ: 61
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
Прямая $$y=-5x+6$$ является касательной к графику функции $$28x^2+23x+c$$. Найдите с.
Ответ: 13
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
Груз массой 0,58 кг колеблется на пружине. Его скорость $$v$$ (в м/с) меняется по закону $$v=v_{0}sin frac{2pi t}{T}$$, где t — время с момента начала колебаний в секундах, Т=6 с — период колебаний, $$v_{0}$$=2 м/с. Кинетическая энергия Е (в Дж) груза вычисляется по формуле $$E=frac{mv^{2}}{2}$$, где m — масса груза (в кг), $$v$$ — скорость груза (в м/с). Найдите кинетическую энергию груза через 4 секунды после начала колебаний. Ответ дайте в джоулях.
Ответ: 0,87
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 21 час. Через 5 часов после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Ответ: 13
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
На рисунке изображена часть графика функции $$f(x)=|kx+b|.$$ Найдите $$f(-15).$$
Ответ: 1,2
Скрыть
$$f(x)$$ проходит через $$(-2;4)$$ и $$(-7;2).$$
При этом изображено «положительное» раскрытие модуля, т. е. $$f(x)=kx+b,kgeq0.$$
Получим:
$$left{begin{matrix} 4=-2k+b\ 2=-7k+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=0,4\ b=4,8 end{matrix}right.$$
Получим:
$$f(x)=|0,4x+4,8|, тогда: f(-15)=|0,4cdot(-15)+4,8|=|-1,2|=1,2.$$
Задание 10
В викторине участвуют 15 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых 8 играх победила команда А. Какова вероятность того, что эта команда выиграет девятый раунд?
Ответ: 0,9
Скрыть
Если команда «А» выиграла n раундов, то вероятность, что команда «А» выиграет в n+1 раунде:
$$1-frac{1}{n+2}$$
Тогда:
$$1-frac{1}{8+2}=1-frac{1}{10}=1-0,1=0,9$$
Задание 11
Найдите наименьшее значение функции $$y=6+frac{sqrt{3}pi}{2}-3sqrt{3}x-6sqrt{3}cos x$$ на отрезке $$[0;frac{pi}{2}]$$
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
а) Решите уравнение: $$cos 4x-sin 2x=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0;pi]$$
Ответ: а)$$frac{pi}{12}+frac{pi k}{3}, kin Z$$ б)$$frac{pi}{12};frac{5pi}{12};frac{3pi}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G — середина ребра SC.
а) Постройте прямую пересечения плоскостей ABG и GDF.
б) Найдите угол между плоскостями ABG и GDF.
Ответ: $$arccos frac{9}{11}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
Решите неравенство: $$9^{x}-10cdot 3^{x+1}+81geq 0$$
Ответ: $$(-infty;1]cup[3;+infty)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2 928 200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Ответ: 9 282 000 рублей
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE.
а) Докажите, что четырёхугольник BCFE — параллелограмм.
б) Найдите площадь четырёхугольника ABCD, если известно, что АВ=6 и АН=$$2sqrt{5}$$.
Ответ: $$48+18sqrt{5}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 17
Найдите все значения а, при каждом из которых функция
$$f(x)=x^{2}-4|x-a^{2}|-8x$$
имеет хотя бы одну точку максимума.
Ответ: $$ain(-sqrt{6};-sqrt{2})cup(sqrt{2};sqrt{6})$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
Имеется 8 карточек. На них записывают по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел -1, 3, 4, -5, 7, -9, -10, 11. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: нет; нет; 16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
| 3577 | В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD |
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525 | |
| 3334 | В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, точка G — середина ребра SC. а) Постройте прямую пересечения плоскостей ABG и GDF. б) Найдите угол между плоскостями ABG и GBF |
а) Постройте прямую пересечения плоскостей ABG и GDF ! 36 вариантов ФИПИ Ященко 2022 Вариант 36 Задание 13 | |
| 3309 | Найдите наибольшее значение функции y=ln((x+9)^5)-5x на отрезке [-8,5; 0] |
Найдите наибольшее значение функции y= ln(x+9)5 -5x на отрезке [-8,5; 0] ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 11 | |
| 3308 | а) Решите уравнение ((0.25)^sin(x))^cos(x)=2^(-sqrt(2)sin(x)) б) Найдите все корни этого уравнения, принадлежащие промежутку [2pi; (7pi)/2]. |
а) Решите уравнение ((0,25) sinx) cosx = 2 -sqrt2 sinx ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 12 | |
| 3307 | На рисунке изображён график функций f(x)=(kx+a)/(x+b). Найдите k
|
На рисунке изображён график функций f(x)= kx+a / (x+b). Найдите k ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 9 | |
| 3306 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точках A(x0; y0) и B(4; 5). Найдите y0
|
На рисунке изображены графики функций, которые пересекаются в точках A(x0; y0) и B(4; 5) ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 9 | |
| 3305 | Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 75 % кислоты. Сколько процентов кислоты содержится в первом сосуде? |
Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 8 | |
| 3304 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точке A. Найдите абсциссу точки A
|
На рисунке изображены графики функций. Найдите абсциссу точки A ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 9 | |
| 3303 | За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки. Найдите вероятность того, что рядом с любым мальчиком будут сидеть две девочки |
За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 10 | |
| 3302 | В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зелёных, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зелёных, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета |
Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета ! 36 вариантов ФИПИ Ященко 2022 Вариант 30 Задание 10 | |

Показана страница 1 из 27
Балаян Э. Н. Геометрия 8 класс. Решебник к книге Э. Н. Балаяна «Геометрия. 7-9 классы». — М.: Феникс, 2019. — 191 с. В предлагаемом пособии приводятся полные решения всех без исключения задач для 8-го класса из книги «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ: 7-9 классы». …
Читать далее…
Решения типовых тестовых заданий ЕГЭ-2018 из сборника Ященко И.В. (36 вариантов). Базовый уровень. — Рукопись. — 2018. Настоящее пособие содержит решения типовых экзаменационных вариантов ЕГЭ-2018 из сборника «ЕГЭ 2018. Математика. Базовый уровень. 36 вариантов. Типовые тестовые задания от разработчиков ЕГЭ / А. В. Антропов, А. В. Забелин, Е. А. Ссмснко, …
Читать далее…
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом. На выполнение экзаменационной работы по математике …
Читать далее…
При ознакомлении с демонстрационным вариантом контрольных измерительных материалов ЕГЭ 2017 г. следует иметь в виду, что задания, включённые в него, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 г. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2017 г., приведён в кодификаторе …
Читать далее…
Демонстрационный вариант предназначен для того, чтобы дать представление о структуре будущих контрольных измерительных материалов, количестве заданий, об их форме и уровне сложности. В демонстрационном варианте представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию будет предложено только одно задание. Задания демонстрационного …
Читать далее…
Найдите площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45°. Решение. Рассмотрим прямоугольную трапецию с основаниями и (см. рис. 1). Проведём высоту .
Читать далее…
Решение 36 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Острые углы прямоугольного треугольника равны 80° и 10°. Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 11. Найдите объём куба.
В сборнике билетов по философии всего 50 билетов, в 6 из них встречается вопрос по теме «Кант». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кант».
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов. Известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,8. Во сколько раз вероятность события «стрелок поразит ровно четыре мишени» больше вероятности события «стрелок поразит ровно три мишени»?
Найдите корень уравнения (log_{5}{(x+7)}=log_{5}(5-x)-1).
Найдите значение выражения (dfrac{20}{(2sqrt{2})^2}).
Прямая (y=6x+7) параллельна касательной к графику функции (y=x^2-5x+6). Найдите абсциссу точки касания.
При адиабатическом процессе для идеального газа выполняется закон (pV^k=7{,}776cdot10^6,Паcdotм^4), где (p) – давление в газе в паскалях, (V) – объём газа в кубических метрах, (k=dfrac{4}{3}). Найдите, какой объём (V) (в куб. м) будет занимать газ при давлении (p), равном (3,75cdot10^6,Па)
Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 53 часа после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
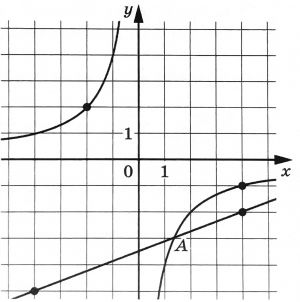
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках А и В. Найдите ординту точки В.
Найдите точку минимума функции (y=-dfrac{x}{x^2+900}).
а) Решите уравнение (4sin^4x+7cos^2x-4=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([-5pi; -4pi]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π | 18. -29π/6 | 19. -19π/4 | 20. -14π/3 |
| 21. -9π/2 | 22. -13π/3 | 23. -17π/4 | 24. -25π/6 |
| 25. -4π | 26. -23π/6 | 27. -15π/4 | 28. -11π/3 |
| 29. -7π/2 |
Основанием пирамиды (FABC) является правильный треугольник (ABC) со стороной (48). Все боковые рёбра пирамиды равны (40). На рёбрах (FB) и (FC) отмечены соответственно точки (K) и (N) так, что (FK=FN=10). Через точки (K) и (N) проведена плоскость (alpha), перпендикулярная плоскости (ABC).
а) Докажите, что плоскость (alpha) делит медиану (AM) в отношении (1:3).
б) Найдите расстояние от точки (C) до плоскости (alpha).
Решите неравенство (3log^2_{4}{(4-x)^8}+4log_{0{,}5}{(4-x)^6}geqslant72)
15 декабря планируется взять кредит в банке на сумму 1 000 000 рублей на (n+1) месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1 378 тысяч рублей.
В треугольнике (ABC) известно, что (AC=26) и (AB=BC=38).
а) Докажите, что средняя линия треугольника, параллельная стороне (AC), пересекает окружность, вписанную в треугольник (ABC).
б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне (AC).
Найдите все значения параметра (a), при каждом из которых любое значение из промежутка ([-1{,}5;-0{,}5]) является решением неравенства ((4|x|-a-3)(x^2-2x-2-a)geqslant0).
Группу детей можно перевезти автобусами модели А или автобусами модели Б. Известно, что в автобусе модели А количество мест больше 40, но меньше 50, а в автобусах модели Б — больше 50, но меньше 60. Если всех детей рассадить в автобусы модели А, то все места будут заняты. Если всех детей рассадить в автобусы модели Б, то все места также будут заняты, но потребуется на один автобус меньше.
а) Может ли потребоваться 4 автобуса модели Б?
б) Найдите наибольшее возможное количество детей в группе, если известно, что их меньше 300.
в) Найдите наибольшее возможное количество автобусов модели А.
Введите ответ в форме строки «да;123;1234». Где ответы на пункты разделены «;», и первый ответ с маленькой буквы.