Решение 10 задания егэ математика профильный уровень 2023 - Помощь в подготовке к экзаменам и поступлению

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник


3633	На рисунке изображён график функции f(x)=k/(x+a). Найдите f(-7) Решение График	На рисунке изображён график функции f(x)=k / x+a Найдите f(-7) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 10

3610	На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков Решение График	На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков ! 36 вариантов ФИПИ Ященко 2023 Вариант 22 Задание 10

3563	На рисунке изображены графики функций f(x)=3x+3 и g(x)=ax^2+bx+c., которые пересекаются в точках A(-1; 0) и B (x0; y0). Найдите y0 Решение График	На рисунке изображены графики функций f(x)=3x+3 и g(x)= ax2 + bx+c ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 10

3507	На рисунке изображён график функции f(x)=a^(x+2). Найдите f(6) Решение График	На рисунке изображён график функции f(x)=a^(x+2). Найдите f(6) ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 10

3482	На рисунке изображены части графиков функций иf(x)=k/x и g(x)=c/x+d. Найдите ординату точки пересечения графиков этих функций Решение	На рисунке изображены части графиков функций. Найдите ординату точки пересечения графиков этих функций ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 10

3456	На рисунке изображен график функции f(x)=acosx+b. Найдите a Решение	На рисунке изображен график функции f(x)=acosx+b ! Тренировочный вариант 397 от Ларина Задание 10

3307	На рисунке изображён график функций f(x)=(kx+a)/(x+b). Найдите k Решение	На рисунке изображён график функций f(x)= kx+a / (x+b). Найдите k ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 9

3306	На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точках A(x0; y0) и B(4; 5). Найдите y0 Решение График	На рисунке изображены графики функций, которые пересекаются в точках A(x0; y0) и B(4; 5) ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 9

3304	На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точке A. Найдите абсциссу точки A Решение График	На рисунке изображены графики функций. Найдите абсциссу точки A ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 9

3301	На рисунке изображён график функции f(x)=a^(x+b). Найдите f(-1) Решение График	На рисунке изображён график функции f(x)=a x+b ! 36 вариантов ФИПИ Ященко 2022 Вариант 29 Задание 9

Источник

Задание 1

Основания равнобедренной трапеции равны 45 и 14. Высота трапеции равна 9,3. Найдите тангенс острого угла.

Ответ: 0,6

Скрыть

Задание 2

Прямоугольный параллелепипед описан около сферы радиуса 2,5. Найдите площадь его поверхности.

Ответ: 150

Скрыть

Задание 3

Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?

Ответ: 0,28

Скрыть

Задание 4

Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Ответ: 0,17

Скрыть

Задание 5

Найдите корень уравнения $$sqrt{frac{50}{5x+45}}=1frac{1}{4}$$

Ответ: -2,6

Скрыть

Задание 6

Найдите значение выражения $$2^{12log_{8}5}$$

Ответ: 625

Скрыть

Задание 7

На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-9;5)$$. Найдите сумму точек экстремума функции $$f(x)$$.

Ответ: -18

Скрыть

Задание 8

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа $$v$$ вычисляется по формуле $$v=ccdotfrac{f-f_{0}}{f+f_{0}}$$ где $$c=1500$$ м/с — скорость звука в воде, $$f_{0}$$ — частота испускаемых импульсов, $$f$$ — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.

Ответ: 220,5

Скрыть

Задание 9

Боря и Ваня могут покрасить забор за 10 часов. Ваня и Гриша могут покрасить этот же забор за 15 часов, а Гриша и Боря — за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?

Ответ: 9

Скрыть

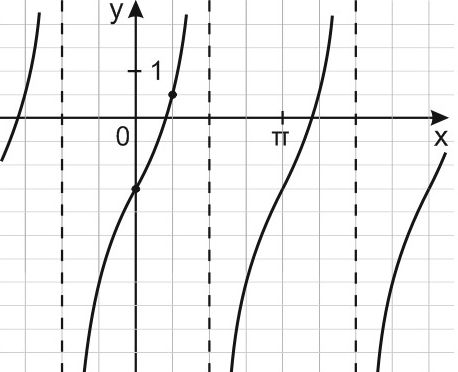
Задание 10

На рисунке изображён график функции $$f(x)=log_{a}(x+3)$$. Найдите значение $$x$$, при котором $$f(x)=16$$.

Ответ: 253

Скрыть

Задание 11

Найдите наименьшее значение функции $$y=e^{2x}-9e^{x}-3$$ на отрезке $$[0; 3]$$.

Ответ: -23,25

Скрыть

Задание 12

а) Решите уравнение $$2sin xcdot sin 2x=2cos x+cos 2x$$.

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};pi]$$.

Ответ: а) $$frac{pi}{4}+frac{pi n}{2};$$$$-frac{2pi}{3}+2pi m;$$$$frac{2pi}{3}+2pi k,$$$$m,n,kin Z$$ б)$$-frac{9pi}{4};-frac{7pi}{4};-frac{4pi}{3};-frac{5pi}{4}$$

Скрыть

Задание 13

Грань ABCD прямоугольного параллелепипеда $$ABCDA_1B_1C_1D_1$$ является вписанной в основание конуса, а сечением конуса плоскостью $$A_1B_1C_1$$ является круг, вписанный в четырёхугольник $$A_1B_1C_1D_1$$: $$AB=a$$, $$AA_1=sqrt{2}$$.

а) Высота конуса равна $$h$$. Докажите, что $$4,5a<h<5a$$.

б) Найдите угол между плоскостями $$ABC$$ и $$SD_1C_1$$, где $$S$$ — вершина конуса.

Ответ: $$arctg(2sqrt{6}+2sqrt{3})$$

Скрыть

Задание 14

Решите неравенство $$log_{5}x^{2}+4log_{25}(6-2x)geqlog_{sqrt{5}}(x^{2}-4)+2log_{0,2}(2-x)$$.

Ответ: $$(-infty;-2)$$

Скрыть

Задание 15

В июле Анна планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Анне оформить кредит на следующих условиях:

— в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая — может быть разным для разных годов);

— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.

В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором — 15, 10 и 20 процентов. Анна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей.

Ответ:

Задание 16

На сторонах $$AB$$ и $$CD$$ четырёхугольника $$ABCD$$, около которого можно описать окружность, отмечены точки $$K$$ и $$N$$ соответственно. Около четырёхугольников $$AKND$$ и $$BCNK$$ также можно описать окружность. Косинус одного из углов четырёхугольника $$ABCD$$ равен 0,2.

а) Докажите, что прямые $$KN$$ и $$AD$$ параллельны.

б) Найдите радиус окружности, описанной около четырёхугольника $$BCNK$$, если радиус окружности, описанной около четырёхугольника $$ABCD$$, равен 7, $$AK:KB=9:10$$, a $$BC<AD$$ и $$BC=10$$.

Ответ: $$frac{5sqrt{22}}{4}$$

Скрыть

Задание 17

Найдите все такие значения $$a$$, при каждом из которых уравнение $$sqrt{10x^{2}-19x-15}cdotlog_{3}(7-(a-4)cdot(x+2))$$ имеет ровно два различных корня.

Ответ: $$4;[frac{16}{3};frac{50}{9});(frac{58}{7};9)$$

Скрыть

Задание 18

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 7735.

а) Может ли последовательность состоять из трёх членов?

б) Может ли последовательность состоять из шести членов?

в) Какое наибольшее количество членов может быть в последовательности?

Ответ: а)нет б)нет в)1933

Скрыть

Источник