Решение и ответы заданий Варианта №12 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
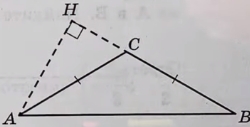
В тупоугольном треугольнике ABC известно, что AC = BC, высота AH равна 3, СН = √7. Найдите синус угла ACB.
Задание 2.
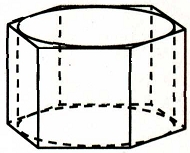
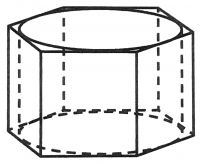
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
Задание 3.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задание 4.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Задание 5.
Найдите корень уравнения 92х+5 = 3,24·52х+5.
Задание 6.
Найдите значение выражения frac{4cos121°}{cos59°}.
Задание 7.
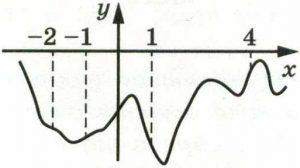
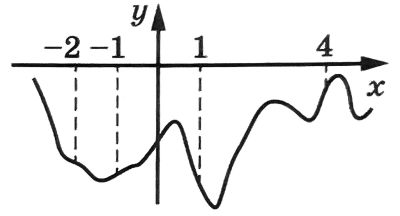
На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, –1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Задание 8.
При температуре 0°С рельс имеет длину l0 = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(𝑡°) = l0(1 + α∙t°), где α = 1,2∙10−5(°С )−1 – коэффициент теплового расширения, t° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.
Задание 9.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно в А со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Задание 10.
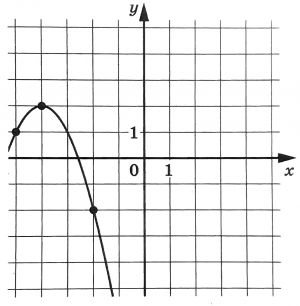
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−9).
Задание 11.
Найдите точку минимума функции y = frac{4}{3}x√x – 5x + 4.
Задание 12.
а) Решите уравнение 2cos3(x – π) = sin(frac{3pi}{2} + x).
б) Найдите все корни уравнения, принадлежащие отрезку [frac{9pi}{2};frac{11pi}{2}].
Задание 13.
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет frac{3}{4} площади треугольника SCD.
б) Найдите объем пирамиды ACDKP.
Задание 14.
Решите неравенство (25х – 4·5х)2 + 8·5х < 2·25x + 15.
Задание 15.
В июле 2023 года планируется взять кредит на 10 лет. Условия его возврата таковы:
– каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
– каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей?
Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC = CD = DE, а AC⊥BE. Точка K – пересечение прямых BE и AD.
а) Докажите, что прямая EC делит отрезок KD пополам.
б) Найдите площадь треугольника ABK, если AD = 4, DC = √3.
Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение
|x^{2}-a^{2}|=|x+a|cdot sqrt{x^{2}-5ax+4a}
имеет ровно два различных корня.
Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 3661 | а) Решите уравнение 2cos^3(x)=-sin((3pi)/2+x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; 4pi]. |
а) Решите уравнение 2cos3 x = -sin(3/2pi+x) ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 12 | |
| 3626 | а) Решите уравнение (x^2+4x-2)*(4^(3x+1)+8^(2x-1)-11)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-0,5; 0,5] |
а) Решите уравнение (x2+4x-2)(4^3x+1+8^2x-1-11) = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 12 | |
| 3619 | а) Решите уравнение 5sin(2x)-5cos(x)+14sin(x)-7=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. |
а) Решите уравнение 5sin2x — 5cosx + 14sinx — 7 = 0 ! Тренировочная работа №1 по математике 10 класс Статград 08-02-2023 Вариант МА2200109 Задание 12 | |
| 3598 | а) Решите уравнение 2sin^2(pi/2-x)+sin(2x)=0 б) Укажите корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. |
а) Решите уравнение 2sin^2(pi/2-x) +sin2x =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 21 Задание 12 | |
| 3595 | а) Решите уравнение 36(log_{1/8}(x))^2+4log_{1/4}(x)-5=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5; 5] |
а) Решите уравнение 36log2 1/8 x-+ 4log1/4 x — 5 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 20 Задание 12 # Ошибка в ответе пособия у Ященко : color{red}{sqrt2/2; 4sqrt2} | |
| 3570 | а) Решите уравнение 15^(sin(x))=3^(sin(x))*5^(-cos(x)) б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. |
а) Решите уравнение 15 sinx =3 sinx 5 -cosx ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 12 Вариант МА2210209 | |
| 3561 | а) Решите уравнение cos(2x)+sin(2x)+1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. |
а) Решите уравнение cos2x + sin2x +1 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 12 | |
| 3551 | а) Решите уравнение 25^(x-0.5)-13*10^(x-1)+4^(x+0.5)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-pi/2; pi]. |
а) Решите уравнение 25^ x-0,5 — 13 10^ x-1 +4^ x+0,5 =0! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 12 | |
| 3536 | а) Решите уравнение 2cos(x)*sin(2x)=2sin(x)+cos(2x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. |
а) Решите уравнение 2cos x sin 2x =2sinx +cos2x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 12 | |
| 3528 | а) Решите уравнение (log_{2}(8x^2))^2-log_{4}(2x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8] |
а) Решите уравнение log2 2(8×2) -log4 (2x) -1 =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 12 | |

Показана страница 1 из 36
В тупоугольном треугольнике ABC известно, что AC=BC, высота AH равна 3, CH=√7. Найдите синус угла ACB.
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 25% этих стёкол, вторая — 75%. Первая фабрика выпускает 5% бракованных стёкол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Найдите корень уравнения (9^{2x+5}=3{,}24cdot 5^{2x+5})
Найдите значение выражения (dfrac{4cos{121°}}{cos{59°}})
На рисунке изображён график (y=f(x)). На оси абсцисс отмечены точки (-2, -1, 1, 4). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
При температуре (0 °C) рельс имеет длину (l_0=15) м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, изменяется по закону (l(t°)=l_0(1+alphacdot t°)), где (alpha=1{,}2cdot 10^{-5}(°C)^{-1}) — коэффициент теплового расширения, (t°) — температура (в градусах Цельсия). При какой температуре рельс удлинится на (7{,}2) мм? Ответ дайте в градусах Цельсия.
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 135 км. На следующий день он отправился обратно со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
На рисунке изображён график функции (f(x)=ax^2+bx+c). Найдите (f(-9)).
Найдите точку минимума функции (y=dfrac{4}{3}xsqrt{x}-5x+4)
а) Решите уравнение (2cos^3{(x-pi)}=sin{left(dfrac{3pi}{2}+xright)})
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[dfrac{9pi}{2};dfrac{11pi}{2}right])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 9π/2 | 18. 14π/3 | 19. 19π/4 | 20. 29π/6 |
| 21. 5π | 22. 31π/6 | 23. 21π/4 | 24. 16π/3 |
| 25. 11π/2 | 26. 17π/3 | 27. 23π/4 | 28. 35π/6 |
| 29. 6π |
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка K — середина бокового ребра SD. Плоскость AKB пересекает боковое ребро SC в точке P.
а) Докажите, что площадь четырёхугольника CDKP составляет 3/4 площади треугольника SCD.
б) Найдите объём пирамиды ACDKP.
Решите неравенство ((25^x-4cdot 5^x)^2+8cdot 5^x<2cdot 25^x+15)
В июле 2023 года планируется взять кредит в банке на 10 лет. Условия его возврата таковы:
– каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
– каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1470 тысяч рублей?
Точки A, B, C, D и E лежат на окружности в указанном порядке, причём BC=CD=DE, а прямые AC и BE перпендикулярны. Точка K — пересечение прямых BE и AD.
а) Докажите, что прямая CE делит отрезок KD пополам.
б) Найдите площадь треугольника ABK, если AD=4, DC=√3
Найдите все значения (a), при каждом из которых уравнение (|x^2-a^2|=|x+a|cdotsqrt{x^2-5ax+4a}) имеет ровно два различных корня.
На доске написано три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих числ быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36
1 вариант с ответами и решением из нового сборника Ященко И.В ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с полным видео разбором варианта, данный вариант вы можете скачать или решать онлайн.
Скачать вариант с ответами
Решать 1 вариант Ященко сборник ЕГЭ 2023
вариант1-ященко-егэ2023-профиль
Полный видео разбор заданий варианта
Задания и ответы для варианта
Задание 1. Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Задание 2. Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Задание 3. Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Задание 4. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Ответ: 0,89
Задание 5. Найдите корень уравнения log3 (5 – 2x) = log3 (1 – 4x) + 1.
Ответ: -0,2
Задание 7. На рисунке изображён график y = f′(x) – производной функции f(x), определенной на интервале (−2; 20). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [1; 15].
Ответ: 5
Задание 9. Моторная лодка прошла против течения реки 96 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Задание 13. В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO. а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией. б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD = 9, BC = 7, SO = 6, а прямая SO перпендикулярна прямой AD.
Ответ:
Задание 15. В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы: – каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; – платежи в 2028 и 2029 годах должны быть равными; – к июлю 2030 года долг должен быть выплачен полностью. Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж в 2028 году?
Ответ: 400000 рублей
Задание 16. В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE. а) Докажите, что AL·AC = AB·ВC. б) Найдите EL, если AC = 21, tg∠BCA = 0,4.
Задание 17. Найдите все значения a, при каждом из которых уравнение (a – x)2 + 4a + 1 = (2x + 1)2 – 8|x| имеет четыре различных корня.
Задание 18. Есть три коробки: в первой коробке 112 камней, во второй – 99, в третья – пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
- а) Могло ли в первой коробке оказаться 103 камня, во второй – 99, в третьей – 9?
- б) Могло ли в третьей коробке оказаться 211 камней?
- в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Вариант статград математика 11 класс ЕГЭ 2023
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 варианты и ответы