Решение 15 задания егэ математика профиль видео - Помощь в подготовке к экзаменам и поступлению

29 сентября 2021

В закладки

Обсудить

Жалоба

Решаем задачи №15 профильного уровня.

Большая подборка задач с ответами: kredity.pdf

Аннуитетные и дифференцированные платежи. Как их не путать?

3 задачи на оптимизацию

Источник

Курс ведёт: Андрей Юрьевич Иванов, кандидат технических наук, преподаватель ЧОУ «Школа Экспресс» Санкт-Петербурга.

Задания №15 в ЕГЭ-2022 по математике профильного уровня — «экономические» задачи на вклады, проценты, кредиты, оптимизацию.

Уровень сложности 2 (из 3). Время решения 10-17 минут.

№ 1. Решение задачи о вкладах (банковских процентах). Методика комплексного анализа и выбор оптимального решения.

№ 2. Решение задачи о кредитах (банковских процентах). Методика комплексного анализа и выбор оптимального решения.

Источник

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

6 лайфхаков по Неравенствам!
1. Помним, что можно делать с неравенствами и чего с ними делать нельзя.
2. Цепочка равносильных преобразований
3. Упрощаем все, что можно!
4. Метод рационализации, он же метод замены множителя.
5. Ошибка с заменой переменной.
6. Проверьте себя!

Поговорим о неравенствах, задача 15 ЕГЭ по математике. Вы знаете, что эту задачу надо решить всем, кто хочет получить на Профильном ЕГЭ не менее 70 баллов. Однако среди неравенств встречаются и нестандартные…

Например, как в этом видео.

И это еще не самое сложное!

Так что же надо знать при решении неравенств?

ВСЕ О НЕРАВЕНСТВАХ

к оглавлению ▴

1. Помним, что можно делать с неравенствами и чего с ними делать нельзя.

— Если умножить обе части неравенства на положительное число, знак неравенства останется тем же. Если на отрицательное – знак неравенства поменяется на противоположный. Умножать (или делить) неравенство на выражение, знак которого неизвестен, — нельзя.

— Возводить обе части неравенства в квадрат можно только если они неотрицательны.

— Извлекать из неравенства квадратный корень – нельзя. Нет такого действия.

— Если в неравенстве есть модуль – раскрывать его надо по строгим правилам, а не просто «с плюсом и с минусом».

А вы знали об этом? Или в первый раз увидели?

к оглавлению ▴

2. Цепочка равносильных преобразований

Оформляем решение как цепочку равносильных преобразований: переходов от неравенства – к системе условий – к следующей системе – и так далее. Все вспомогательные преобразования (например, решение квадратных уравнений) делаем на полях.

Почему-то в этом году при решении неравенств стало модно писать: «Ограничения». При этом никто не дал определения – что такое «ограничения», как они связаны с ОДЗ. В математической литературе такой термин не встречался. Чтобы избежать этих сложностей, лучше оформлять решение как цепочку равносильных переходов. Об этом я говорила на Онлайн-курсе.

к оглавлению ▴

3. Упрощаем все, что можно!

Чтобы не решать неравенства через …ну сами знаете что. Например, дроби раскладываем на сумму дробей.

Каким образом упрощать? – Об этом я весь год рассказывала на Онлайн-курсе. Тем, кому сдавать ЕГЭ через 2 месяца — есть отличное предложение тут.

4. Метод рационализации, он же метод замены множителя.

Как? Тоже не знаете такого? Зря! Смотрите Онлайн-курс.

Кстати, в эту субботу – занятие по неравенствам. Еще не поздно! Сейчас стоимость курса для 11 класса всего ~~4800 руб~~ 2 900 руб!

У вас будет доступ ко всем темам и задачам ЕГЭ, ДЗ с проверкой и майским маттренингам! Присоединяйтесь!

к оглавлению ▴

5. Ошибка с заменой переменной.

Знаете, что может быть самое обидное, когда вы решаете неравенство на экзамене? Самое обидное, просто epic fail – когда вы правильно нашли все границы интервалов… а сами интервалы записали с точностью до наоборот! Аааа, ноль баллов! Как этого избежать?

Так происходит, если вы сделали замену переменной, а к старой переменной вернулись некорректно. Помните: сначала полностью решить неравенство относительно новой переменной. И только после этого вернуться к исходной.

к оглавлению ▴

6. Проверьте себя!

Получив ответ, подставьте 2-3 точки из найденных интервалов в исходное неравенство. Полной гарантии этот метод не дает, но хоть очевидных ошибок не сделаете.

А если хотите полной гарантии – вам к нам на Онлайн-курс.

Лучше всего выбирать формат «Подготовка на 100 баллов», если вы в 11-м классе. Формат «для преподавателей», если вы учитель или репетитор. А если вы в 10-м классе – формат «10 + 11». В нем вы сейчас получите доступ к программе 10 класса, а с сентября — к программе 11 класса. Таким образом, летом у вас будет время закрыть пробелы, возникшие в 10 классе.

Сейчас распродажа, все предложения очень выгодные!

Кстати. Напишите нам на почту online@ege-study.ru , какие еще лайфхаки нужны. По каким задачам. Расскажем все секреты!

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «6 лайфхаков Анны Малковой для задачи 15 ЕГЭ по математике (Неравенства). И новый видеоразбор!» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
10.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Источник

В статье представлен разбор задания 15 из ЕГЭ по математике профильного уровня. Для вашего удобства представлен также видеоразбор решения этого задания с подробными комментариями от репетитора по математике.

Решите неравенство:

$[ frac{49^x-6cdot 7^x+3}{7^x-5}+frac{6cdot 7^x-39}{7^x-7}leqslant 7^x+5. ]$

Заметим, что . Введём замену . Тогда неравенство примет вид:

$[ frac{t^2-6t+3}{t-5}+frac{6t-39}{t-7}leqslant t+5. ]$

Переносим всё члены в левую сторону относительно знака неравенства, приводим всё к общему знаменателю, раскрываем скобки и приводим подобные слагаемые. В результате чего получаем следующее неравенство:

$[ frac{t-1}{(t-5)(t-7)}leqslant 0. ]$

Решаем его с помощью метода интервалов:

Определяем область допустимых значений (ОДЗ) выражения, стоящего слева от знака неравенства. В эту область входят все числа, но и , поскольку при данных значениях t знаменатель обращается в нуль.
Определяем значения t, при которых выражение равно нулю. Дробь равна нулю, когда нулю равен её числитель, а знаменатель не равен нулю. То есть это одно единственное значение: .
Наносим полученные значения, а также значения, которые не входят в ОДЗ, на числовую прямую. После этого определяем знаки выражения в каждом из полученных промежутков на числовой прямой и выбираем те, на которых выражение меньше или равно нулю:

$[ left[ begin{array}{l} 0 < tleqslant 1 \ 5 < t < 7. end{array} ]$

Далее переходим к обратной подстановке:

$[ left[ begin{array}{l} 0 < 7^xleqslant 1 \ 5< 7^x < 7. end{array} ]$

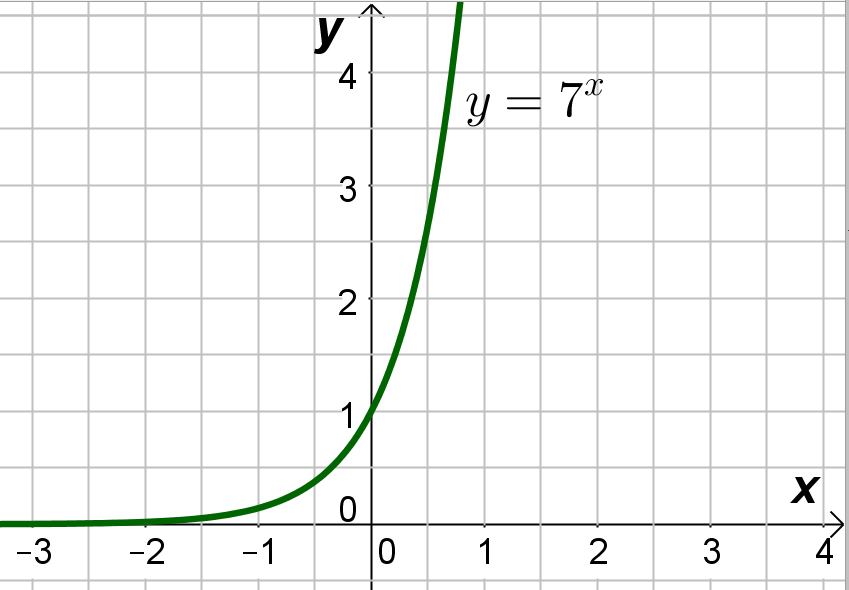
Разбираемся сперва с первым двойным неравенством данной совокупности. Условие выполняется при любых значениях x, так как показательная функция всегда положительна (её график изображён на рисунке снизу). Кроме того, эта функция является возрастающей (большие значения x соответствуют большим значениям y) и равна 1 при . То есть при меньших значениях x функция будет меньше 1. Итак, решением первого двойного неравенства совокупности является промежуток: .

Для решения второго двойного неравенства совокупности также используем свойство возрастания функции . В силу возрастания этой функции, чтобы узнать, при каких значениях её аргумента значения функции находятся в промежутке , достаточно узнать, при каких значениях аргумента и значения функции равны 5 и 7. Тогда решение двойного неравенства будет иметь вид: . Итак, $7^{x_1}=5$ , откуда , и $7^{x_2}=7$ , откуда . То есть решение данного двойного неравенства имеет вид: .

Окончательный ответ: $xin(-mathcal{1};0]cup(log_7 5;1)$ .

Материал подготовлен репетитором по математике в Москве, Сергеем Валерьевичем

Источник

Статьи

Среднее общее образование

Математика

Алгебра

Вашему вниманию мы предлагаем видеообзор, в котором учитель математики Алексей Владимирович Доронин подробно разбирает решение задания 15 из ЕГЭ-2018 по математике профильного уровня. Для успешной подготовки к ЕГЭ по математике мы также подобрали несколько материалов, опубликованных ранее.
Всем зарегистрированным пользователям материал доступен для скачивания.

29 марта 2018

Задание 15

Актуальная информация по заданию в материалах по ссылке:

Задание 15 ЕГЭ-2019

Решите неравенство:

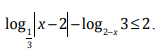
Решение:

Заметим, что:

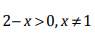
поэтому модуль раскрываем со знаком минус и приходим к следующему неравенству:

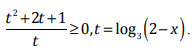
Решая неравенство относительно t, получаем t = —1; t > 0. Возвращаясь к переменной x, получаем следующие значения:

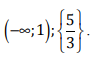
Учитель математики высшей категории, гимназия № 1520 им. Капцовых, лауреат Всероссийского конкурса «Учитель года России — 2011», победитель конкурса лучших учителей на денежное поощрение (в рамках ПНПО) – 2011, лауреат Всероссийского конкурса учителей фонда «Династия», лауреат Всероссийского конкурса учебно-методических разработок по преподаванию основ финансовой грамотности 2016

Источник