Решение 17 номера егэ информатика на питоне - Помощь в подготовке к экзаменам и поступлению

Привет! Сегодня поговорим о 17 задании ЕГЭ по информатике 2022.

В 17 задании нужно считать числа из файла, проанализировать их и ответить на вопрос задачи.

Будем решать задание на языке Python.

Задача (Минимальное значение)

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых оба числа делятся нацело на 7, затем минимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 7; 14; 21; -7; 4 — ответ 3 14.

Решение:

Напишем программу на языке Python.

f=open('17_1.txt')

count=0
sm=20000

n1=int(f.readline())

for s in f.readlines():
    n2=int(s)

    if n1%7==0 and n2%7==0:
        count=count+1
        sm=min(n1+n2, sm)
    
    n1=n2

print(count)
print(sm)

В начале подвязываемся к файлу с помощью команды open().

Переменная count отвечает за количество пар, удовлетворяющих условию задачи. Переменная sm — это минимальная сумма элементов подходящих пар.

В начале в переменную sm кладём максимальное число, которое теоретически может получится (10000 + 10000). Это делается для того, чтобы это значение можно было легко «победить» при поиске минимального значения.

Затем считываем в переменную n1 первое число. C помощью конструкции «for s in f.readlines():» можно перебрать остальные числа из файла. В цикле считываем второе число для пары в переменную n2.

После того, как два числа у нас есть, мы анализируем эти элементы на условие задачи. Если одновременно два числа из пары делятся на 7, то мы подсчитываем такую пару.

Если пара подходит, то проверяем сумму элементов этой пары на минимальность. В переменную sm заносится минимальное значение из прежнего значения sm и претендующего нового значения n1+n2.

В конце цикла нужно переложить второе число в переменную n1, чтобы очередное число из файла считалось в переменную n2. Тем самым мы получим новую пару чисел.

Ответ:

Задача (Проверяем на что оканчивается число)

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых оба числа оканчиваются или на 3, или на 5 (можно неодновременно), затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 3; 15; 25; -3; 4 — ответ 3 40.

Решение:

f=open('17_2.txt')

count=0
sm=-20000

n1=int(f.readline())

for s in f.readlines():
    n2=int(s)

    if (abs(n1)%10==3 or abs(n1)%10==5) and (abs(n2)%10==3 or abs(n2)%10==5):
        count=count+1
        sm=max(n1+n2, sm)
    
    n1=n2

print(count)
print(sm)

Т.к. мы ищем максимальную сумму, то в начале в переменную sm кладём наоборот минимальное значение (-10000-10000=-20000).

Когда ищем на что оканчивается положительное число, мы применяем конструкцию x%10. Т.е. находим остаток от деления на 10. Пример: 16 % 10 = 6. Но для отрицательных чисел это не работает -16 % 10 = 4. Почему такой ответ получается, можете посмотреть в этом видео: https://www.youtube.com/watch?v=BRfgE3pP0_c. Поэтому, чтобы правильно найти на что оканчивается число, применяем функцию abs(), что означает модуль числа.

Здесь мы должны логические выражения для первого и второго числа взять в скобки, потому что логическая операция И имеет приоритет перед ИЛИ.

Ответ:

Задача (Полный квадрат)

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10000 до 10000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число является полным квадратом некоторого натурального числа, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два подряд идущих элемента последовательности. Например для последовательности из пяти элементов: 9; 15; 23; -3; 4 — ответ 2 24.

Решение:

f=open('17_3.txt')

count=0
sm=-20000

n1=int(f.readline())

for s in f.readlines():
    n2=int(s)

    if (n1>0 and (int(n1 ** 0.5) ** 2) == n1) or (n2>0 and (int(n2 ** 0.5) ** 2) == n2) :
        count=count+1
        sm=max(n1+n2, sm)
    
    n1=n2

print(count)
print(sm)

Здесь мы извлекаем корень из числа с помощью возведения в степень 0.5. Округляем результат в меньшую сторону с помощью функции int(). А затем снова возводим в квадрат. Если мы получили изначальное число, значит, это число и есть полный квадрат некоторого натурального числа.

Возведение в степень в 0.5 работает и для отрицательных чисел. Т.к. в задаче имеют ввиду квадраты натуральных чисел, то мы работаем только с числами, которые больше нуля.

Ответ:

Задача (Тройки чисел)

(А. Кабанов) В файле 17-3.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество троек элементов последовательности, в которых числа расположены в порядке возрастания, затем минимальную из разностей наибольшего и наименьшего элементов таких троек. В данной задаче под тройкой подразумевается три идущих подряд элемента последовательности.

Источник задачи: https://kpolyakov.spb.ru/

Решение:

f=open('17-3.txt')

count=0
rz=20000

n1=int(f.readline())
n2=int(f.readline())

for s in f.readlines():
    n3 = int(s)

    if n1 < n2 < n3:
        count=count+1
        mx = max(n1, n2, n3)
        mn = min(n1, n2, n3)
        rz = min(rz, mx-mn)

    n1=n2
    n2=n3


print(count, rz)

С тройками решаем аналогично. До цикла считываем два числа. Внутри цикла считываем третье число.

В конце цикла перекладываем числа: второе число в n1, третье число в n2.

Ответ:

Задача (Любой порядок элементов)

В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 9, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.

Источник задачи: https://inf-ege.sdamgia.ru/

Решение:

Первый способ (Красивый).

f = open('17.txt')

count_0 = 0
count_1 = 0
count_2 = 0
count_3 = 0
count_4 = 0
count_5 = 0
count_6 = 0
count_7 = 0
count_8 = 0


mx1_0 = 0
mx2_0 = 0
mx_1 = 0
mx_2 = 0
mx_3 = 0
mx_4 = 0
mx_5 = 0
mx_6 = 0
mx_7 = 0
mx_8 = 0


for s in f.readlines():
    n=int(s)

    if n%9==0:
        count_0 = count_0 + 1

        if n>mx1_0:
            if n>mx2_0:
                mx1_0 = mx2_0
                mx2_0 = n
            else:
                mx1_0 = n

    if n%9==1:
        count_1 = count_1 + 1
        mx_1 = max(mx_1, n)

    if n%9==2:
        count_2 = count_2 + 1
        mx_2 = max(mx_2, n)

    if n%9==3:
        count_3 = count_3 + 1
        mx_3 = max(mx_3, n)

    if n%9==4:
        count_4 = count_4 + 1
        mx_4 = max(mx_4, n)

    if n%9==5:
        count_5 = count_5 + 1
        mx_5 = max(mx_5, n)

    if n%9==6:
        count_6 = count_6 + 1
        mx_6 = max(mx_6, n)

    if n%9==7:
        count_7 = count_7 + 1
        mx_7 = max(mx_7, n)

    if n%9==8:
        count_8 = count_8 + 1
        mx_8 = max(mx_8, n)


count = (count_1*count_8) + (count_2*count_7)  + (count_3*count_6) + (count_4*count_5) + (count_0*(count_0-1)//2)
mx = max(mx_1 + mx_8, mx_2 + mx_7, mx_3 + mx_6, mx_4 + mx_5, mx1_0 + mx2_0)

print(count, mx)

Здесь мы ищем количество элементов, у которых остаток при делении на 9 равен нулю, единице, двойке, … и до 8. Подсчитываем эти данные соответственно в переменные count_0, count_1, count_2 … и т.д.

Так же находим максимальное число, которое имеет при делении на 9 остаток равный единице, двойке, … и т.д. Для чисел, которые имеют остаток при делении на 9 ноль, находим два максимальных числа.

После того, как результаты находятся в нужных переменных, можно вычислить ответ к задаче.

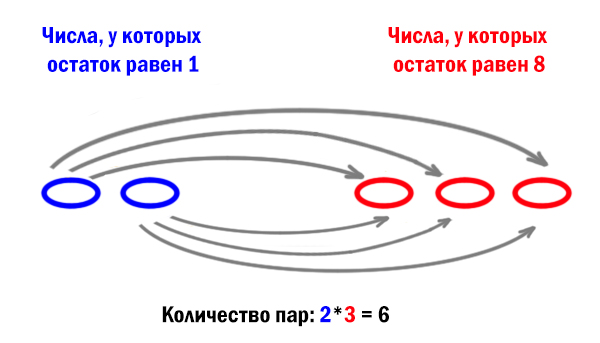
Если, к примеру, взять число для которого остаток равен 1 и число для которого остаток равен 8, то их сумма будет делится на 9. Найдём количество пар, если нам известно количество и тех, и тех чисел.

Значит, просто нужно перемножить два числа, к примеру, count_1*count_8.

Для чисел, которые делятся на 9 (т.е. остаток равен нулю), количество пар считается немного по-другому. Такие числа можно суммировать между собой, всё равно сумма тоже будет делится на 9. Путь есть у нас количество чисел count_0, которые делятся на 9. Тогда найдём количество пар, которые можно составить из этих элементов.

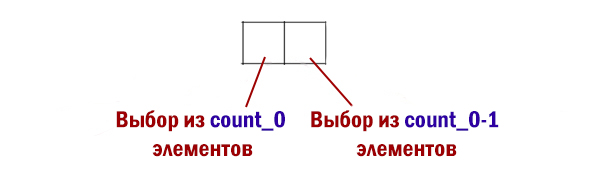
Здесь вспомним метод умножения, о котором было написано в этой статье.

Найдём количество таких пар, если каждый элемент можно использовать 1 раз. Получается count_0*(count_0-1). Но т.к. в нашем случае пара, когда элементы находятся в одном порядке и в обратном, является одной и той же, то нужно это количество поделить на 2. Т.е количество пар будет (count_0*(count_0-1))/2.

Второй способ (Перебор).

f = open('17.txt')

count=0
mx=0

a = []

#Считываем все числа в массив a
for s in f.readlines():
    n = int(s)
    a.append(n)

# Перебираем все варианты и подсчитываем пары, отвечающие условию задачи.
for i in range(0, len(a)):
    for j in range(i+1, len(a)):
        if (a[i]+a[j])%9==0:
            count = count + 1
            mx = max(a[i]+a[j], mx)
    

print(count, mx)

В этом решении сначала считываем все числа в массив a.

Далее берём число и начинаем его комбинировать со всеми числами, которые стоят после этого числа. Таким образом, мы переберём все возможные комбинации, и у нас не будут пары повторяться.

Ответ:

Источник

№1

f=open(’17_1.txt’)
a=[int(x) for x in f]
minimum=min(a)
k=0
max_summa=0
s1=0
k1=0
for i in range(len(a)):
if a[i]%4==0:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (a[i]%minimum==0 and a[i]+a[i+1]or (a[i+1]%minimum==0 and a[i]+a[i+1] k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)

Ответ: 1428 829

№2

f=open(’17_2.txt’)
a=[int(x) for x in f]
maximum=max(a)
k=0
min_summa=10000000000000
s1=0
k1=0
for i in range(len(a)):
if a[i]%10==3:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (maximum%a[i]==0 and a[i]+a[i+1]sr_ar) or (maximum%a[i+1]==0 and a[i]+a[i+1]sr_ar):
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)

Ответ: 72 795

№3

f=open(’17_3.txt’)
a=[int(x) for x in f]
k=0
max_summa=0
for i in range(len(a)-1):
if a[i]%5==0 and a[i+1]%5==0:
k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)

Ответ: 213 965

№4

f=open(’17_4.txt’)
a=[int(x) for x in f]
k=0
min_summa=10000000000000
for i in range(len(a)-1):
if a[i]%20 or a[i+1]%20:
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)

Ответ: 3741 -973

№5

def h(ch):
k6 = 0
while ch0:
ost=ch%10
if ost==6:
k6=k6+1
ch=ch//10
return k6
f=open(’17_5.txt’)
a=[int(x) for x in f]
k=0
m=1000000000000000
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=min(a[i],m)
print(k,m)

Ответ: 935 -496

№6

def h(ch):
k4 = 0
while ch0:
ost=ch%10
if ost==4:
k4=k4+1
ch=ch//10
return k4
f=open(’17_6.txt’)
a=[int(x) for x in f]
k=0
m=0
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=max(a[i],m)
print(k,m)

Ответ: 1753 499

№7

f=open(’17_7.txt’)
a=[int(x) for x in f]
k=0
max_razn=0
for i in range(len(a)-1):
if a[i]a[i+1]:
k=k+1
max_razn=max(max_razn,a[i]-a[i+1])
print(k,max_razn)

Ответ: 2514 963

№8

f=open(’17_8.txt’)
a=[int(x) for x in f]
k=0
min_razn_kv=100000000000
for i in range(len(a)-1):
if a[i]0 and a[i+1]0 and a[i+1]a[i]:
k=k+1
min_razn_kv=min(min_razn_kv,a[i+1]**2-a[i]**2)
print(k,min_razn_kv)

Ответ: 670 171

№9

f=open(’17_9.txt’)
a=[int(x) for x in f]
m=0
k=0
for i in range(len(a)):
if a[i]%4==0 and a[i]%5!=0 and a[i]%8!=0 and a[i]%31!=0 and a[i]%41!=0:
k=k+1
m=max(m,a[i])
print(m,k)

Ответ: 9572 381

№10

f=open(’17_10.txt’)
a=[int(x) for x in f]
m=100000000000
k=0
for i in range(len(a)):
if a[i]%7==0 and a[i]%5==0 and a[i]%2!=0 and a[i]%11!=0 and a[i]%91!=0:
k=k+1
m=min(m,a[i])
print(m,k)

Ответ: -8785 43

№11

f=open(’17_11.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%2==0 and a[i]%30:
k=k+1
b.append(a[i])
b.sort(reverse=True)
print(k,b[1])

Ответ: 1299 9664

№12

f=open(’17_12.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%3==0 and a[i]%20:
k=k+1
b.append(a[i])
b.sort()
print(k,b[1])

Ответ: 669 -9777

№13

f=open(’17_13.txt’)
a=[int(x) for x in f]
k=0
m=100000000000000000
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]a[i] and a[i+1]a[i+2]:
k=k+1
m=min(m,a[i+1])
print(k,m)

Ответ: 1335 -8615

№14

f=open(’17_14.txt’)
a=[int(x) for x in f]
k=0
m=0
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]or a[i+1]2] or a[i+1]and a[i+1]2]:
k=k+1
m=max(m,a[i+1])
print(k,m)

Ответ: 2661 9435

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 204 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 5, а их сумма делится на 7. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (2 5 9 8 10) есть две подходящие пары: (2 5) и (5 9), в ответе для этой последовательности надо записать числа 2 и 14.

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар чисел, произведение которых кратно 15, а их сумма делится на 7. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём тройкой три идущих подряд элемента последовательности. Определите количество троек чисел таких, которые могут являться сторонами остроугольного треугольника. В ответе запишите два числа: сначала количество найденных троек, а затем  — максимальную сумму элементов таких троек. Если таких троек не найдётся  — следует вывести 0 0.

Задание 17

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём тройкой три идущих подряд элемента последовательности. Определите количество троек чисел таких, которые могут являться сторонами прямоугольного треугольника. В ответе запишите два числа: сначала количество найденных троек, а затем  — максимальную сумму элементов таких троек. Если таких троек не найдётся  — следует вывести 0 0.

Задание 17

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 3 и хотя бы один из двух элементов меньше среднего арифметического всех чётных элементов последовательности. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (3 8 9 4) есть две подходящие пары: (3 и (9 4), в ответе для этой последовательности надо записать числа 2 и 13.

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 5 и хотя бы один из двух элементов меньше среднего арифметического всех элементов последовательности, значение которых нечетно. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (8 10 2 9 5) есть две подходящие пары: (10 2) и (9 5), в ответе для этой последовательности надо записать числа 2 и 14.

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых один из двух элементов делится на 3, а другой меньше среднего арифметического всех чётных элементов последовательности. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (1 3 8 9 4) есть две подходящие пары: (1 3) и (9 4), в ответе для этой последовательности надо записать числа 2 и 13.

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых один из двух элементов делится на 5, а другой меньше среднего арифметического всех нечётных элементов последовательности. В ответе запишите два числа: сначала количество найденных пар, а затем  — максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (8 10 2 7 5 1) есть две подходящие пары: (10 2) и (5 1), в ответе для этой последовательности надо записать числа 2 и 12.

Ответ:

Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 3, а их сумма делится на 5. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар.

Задание 17

Например, в последовательности (2 3 7 8 9) есть две подходящие пары: (2 3) и (3 7), в ответе для этой последовательности надо записать числа 2 и 10.

Ответ:

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от −10 000 до 10 000 включительно. Определите количество пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

Задание 17

Ответ:

Источник: Демонстрационная версия ЕГЭ−2023 по информатике

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень, увеличить количество камней в первой куче в два раза или увеличить количество камней во второй куче в три раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 27). Чтобы делать

ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 84. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 84 или больше камней.

В начальный момент в первой куче было 16 камней, во второй куче  — S камней, 1 ≤ S ≤ 67.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т.е не гарантирующие выигрыш независимо от игры противника.

Выполните следующие задания.

Задание 1.

Назовите все значения S, при которых Петя может выиграть первым ходом.

Задание 2.

Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети.

Задание 3.

Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). В узлах дерева указывайте игровые позиции. Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не будет верным ответом на это задание.

Задания Д26 C3 № 5502

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 36. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 36 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 35.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1.  а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.

б)  Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2.  Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.

3.  Укажите значение S, при котором:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 1.

Задания Д26 C3 № 7471

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 18 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 35. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 35 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 34. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Задание 1

а)  Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающие ходы.

Задание 2

Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

− Петя не может выиграть за один ход;

− может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Для каждого указанного значения S опишите выигрышную стратегию Пети.

Задание 3

Укажите значение S, при котором одновременно выполняются два условия:

− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани.

Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте, кто делает ход; в узлах  — количество камней в позиции.

Источник: Демонстрационная версия ЕГЭ—2015 по информатике.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может

добавить в одну из куч один камень или

увеличить количество камней в куче в два раза.

Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (12, 9), (6, 10), (6, 18). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 47 или больше камней.

В начальный момент в первой куче было 11 камней, во второй куче  — S камней, 1 ≤ S ≤ 35.

Выполните следующие задания.

Задание 1.

а)  Назовите все значения S, при которых Петя может выиграть первым ходом.

б)  Петя сделал неудачный первый ход, после которого Ваня выиграл своим первым ходом. Назовите минимальное значение S, при котором это возможно.

Задание 2. Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети

Задание 3. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может

добавить в кучу один камень или

добавить в кучу два камня или

увеличить количество камней в куче в два раза.

Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 12 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче превышает 37. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 38 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 37.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

Выполните следующие задания.

Задание 1.

а)  Назовите все значения S, при которых Петя может выиграть первым ходом, причём у Пети есть ровно один выигрывающий ход.

Задание 2.

Укажите три значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.

Задание 3.

Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не будет верным ответом на это задание.

Игра завершается в тот момент, когда количество камней в куче превышает 54. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 55 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 54.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Задание 1

Задание 2

− Петя не может выиграть за один ход

− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Для каждого указанного значения S опишите выигрышную стратегию Пети.

Задание 3

Укажите значение S, при котором одновременно выполняются два условия:

− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани.

добавить в кучу один камень или

добавить в кучу два камня или

увеличить количество камней в куче в два раза.

Игра завершается в тот момент, когда количество камней в куче превышает 41. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 42 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 41.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

Выполните следующие задания.

Задание 1.

Задание 2.

Задание 3.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 68.

Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 68 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 67.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Выполните следующие задания.

Задание 1

а)  Укажите все такие значения числа S, при которых Петя может выиграть за один ход.

Задание 2

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Для каждого указанного значения S опишите выигрышную стратегию Пети.

Задание 3

Укажите значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах  — количество камней в куче. Дерево не должно содержать партии, невозможные при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.

Источник: ЕГЭ по информатике 2020. Досрочная волна. Вариант 2

Задания Д26 C3 № 5726

Игра завершается в тот момент, когда количество камней в куче становится не менее 40. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 40 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 39.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

3.  Укажите значение S, при котором:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 2.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или из 40 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче превышает 64. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 65 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 64.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

Выполните следующие задания.

Задание 1.

а)  Назовите все значения S, при которых Петя может выиграть первым ходом.

Задание 2.

Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.

Задание 3.

Всего: 204 1–20 | 21–40 | 41–60 | 61–80 …

Источник

На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 17 задания. Объясняется тема о программной обработке числовой информации.

Содержание:

ЕГЭ по информатике 17 задания объяснение
Выполнение 17 задания ЕГЭ
- Работа с цифрами числа в n-й системе счисления

17-е задание: «Программная обработка целочисленной информации»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 1,

Примерное время выполнения

— 15 минут.

Проверяемые элементы содержания: Умение создавать собственные программы (20–40 строк) для обработки целочисленной информации

Выполнение 17 задания ЕГЭ

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

17_1: Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [1016; 7937], которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них.
В ответе запишите два целых числа: сначала количество, затем максимальное число.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Типовые задания для тренировки

Ответ: 1568 | 7935

Видео

✍ Решение:

✎ Решение с использованием программирования:

Паскаль:

var
  i, k, max: integer;
 
begin
  k := 0;
  max := 0;
  for i := 1016 to 7937 do 
  begin
    if (i mod 3 = 0) and (i mod 7 > 0) and (i mod 17 > 0) and (i mod 19 > 0) and (i mod 27 > 0) then
    begin
      max:= i;
      inc(k);
    end;
  end;
  writeln(k, ' ', max)
end.

PascalABC.NET:

begin
 var s := Range( 1017, 7937, 3).Where( i -> not i.DivsAny(7, 17, 19, 27) );
 print( s.Count, s.Max );            
end.

Python:

1
2
3

a = [n for n in range(1016,7937+1) 
     if (n%3==0 and n%7!=0 and n%17!=0 and n%19!=0 and n%27!=0)]
print(len(a),max(a))

Список a формируем, используя генератор списка: то есть в список попадут только не числа из диапазона [1016,7937], которые удовлетворяют всем перечисленным условиям: n%3==0 (число делится на 3), n%7!=0 (число не делится на 7) и т.п.

C++:

#include <iostream>
int main()
{
  int count = 0;
  int maxGood = 0;
  for(int n=1016; n<=7937; n++)
    if( (n % 3 == 0) and (n % 7 != 0) and 
        (n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0) ) {
      maxGood = n;    
      count += 1;
      }  
  std::cout << count << " " << maxGood;
}

✎ Решение с помощью Excel:

Первое значение диапазона введем в ячейку A1:

Используем прогрессию для заполнения всего диапазона числами. Для это выберите вкладку Главная и щелкните по кнопке Прогрессия:

Столбец B будем использовать для поиска чисел, которые делятся на 3. Для этого в ячейку B1 введите формулу с рисунка:

Двойным щелчком по маркеру заполнения скопируйте формулу на весь столбец:

Столбец С будем использовать для поиска чисел, которые НЕ делятся на 7. Для этого в ячейку С1 введите формулу с рисунка:

Заполните весь столбец двойным щелчком по маркеру заполнения.
Cтолбцы D, E, F таким же образом будем использовать для поиска чисел столбца А, которые не делятся на 17, 19 и 27

Для поиска всех истинных значений используем столбец G. В ячейку G1 введите функцию ЕСЛИ: если все значения ячеек в столбцах B-F в этой строке истинны, выводим число из А1, иначе – пустую строку:

Заполните весь столбце, используя маркер автозаполнения.

Ячейку H1 будем использовать для подсчета таких чисел, которые удовлетворяют всем условиям, т.е. для подсчета непустых ячеек столбца G:

Ячейку H2 будем использовать для подсчета такого наибольшего числа:

Видеоразбор 17 задания ЕГЭ:
📹 YouTube здесь

Видеорешение на RuTube здесь

Работа с цифрами числа в n-й системе счисления

17_2:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [3712; 8432], которые удовлетворяют следующим условиям:
− запись в двоичной и четверичной системах счисления заканчивается одинаковой цифрой;
− кратны 13, 14 или 15.

Найдите количество таких чисел и минимальное из них.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Типовые задания для тренировки

Ответ: 471 3720
✍ Решение:

✎ Решение с использованием программирования:

Паскаль:

var
 var k, n, min:integer;
 
begin
  k:=0; min:=8433;
  for n:= 3712 to 8432 do
    if (n mod 2 = n mod 4) and ((n mod 13=0) or (n mod 14=0) or (n mod 15=0)) then
      begin
        if min>n then
        min:=n;
        k:=k+1;
      end;
      Writeln (k,' ',min);
End.

PascalABC.NET:

begin
 var s := Range( 3712, 8432)
   .Where(i -> ((i mod 13=0) or (i mod 14=0) or (i mod 15=0)) and (i mod 2 = i mod 4));
    // или: .Where( i -> (i.DivsAny(13,14,15)) and (i mod 2 = i mod 4));
 s.Count.Print;
 s.Min.Print;  
end.

Python:

1 2	L = [x for x in range(3712, 8432+1) if (x % 13 == 0 or x % 14 == 0 or x % 15 == 0) and ( x % 2 == x % 4)] print(len(L),' ',L[0])

Формируем список (массив) L только из подходящих элементов, то есть удовлетворяющих всем, перечисленным в задании, условиям. Затем выводим длину списка (len(L)), т.е. найденное количество таких чисел, и нулевой элемент, он же минимальный, поскольку числа упорядочены по возрастанию (L[0])

C++:

#include <iostream>
int main()
{
	int count = 0;
	int min = 8433;
	for (int n = 3712; n <= 8432; n++)
		if (((n % 2 == n % 4) && ((n % 13 == 0) || (n % 14 == 0) || (n % 15 == 0))) )
		{
			if (n < min) min = n;
			count += 1;
		}
	std::cout << count << " " << min;
}

✎ Решение с помощью Excel:

Первое значение диапазона введем в ячейку A1:

Используем прогрессию для заполнения всего диапазона числами. Для это выберите вкладку Главная и щелкните по кнопке Прогрессия:

Столбец B будем использовать для поиска чисел, которые кратны 13, 14 или 15. Для этого в ячейку B1 введите формулу с рисунка:

Двойным щелчком по маркеру заполнения скопируйте формулу на весь столбец:

Столбец С будем использовать для поиска чисел, запись которых в двоичной и четверичной системах счисления заканчивается одинаковой цифрой. Для этого в ячейку С1 введите формулу с рисунка:

Заполните весь столбец двойным щелчком по маркеру заполнения.

Для поиска всех истинных значений используем столбец D. В ячейку D1 введите функцию ЕСЛИ: если все значения ячеек в столбцах B, C в этой строке истинны, выводим число из А1, иначе – пустую строку:

Заполните весь столбце, используя маркер автозаполнения.

Ячейку E1 будем использовать для подсчета таких чисел, которые удовлетворяют всем условиям, т.е. для подсчета непустых ячеек столбца D:

Ячейку E2 будем использовать для подсчета такого наименьшего числа (или просмотрите столбец D визуально и найдите первое значение):

17_3:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [1000; 9999], запись которых в пятеричной системе имеет не менее 6 цифр и заканчивается на 21 или 23.

Найдите количество таких чисел и минимальное из них.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Ответ: 550 3136

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

### uses school;
var s := Range(1000, 9999)
   .Where(i -> (i.ToString.ToBase(5).Length=6) and (i div 5 mod 5 = 2)
       and((i mod 5 = 1) or (i mod 5 = 3)));
s.Count.Print;
s.Min.Print;

Python:

numb=''
result=list()
for i in range(1000, 9999+1):
    if ((i // 5) % 5 ==2) and (( i % 5 == 1) or ( i % 5 == 3)):
        while i>=5: #Цикл перевода числа из 10-й в 5-ю сс
            s=i%5
            numb=str(s)+numb
            i=i//5
            if i<5:
                numb=str(i)+numb
        n=len(numb)
        if n>5:
            result.append(numb) # список из чисел в 5-й с.с
        numb=""
kolvo=len(result)
minNumb=int(min(result),5) # перевод в десятичную с.с и поиск min
print(kolvo,minNumb)

Источник

Разбор 17 задания на Python | ЕГЭ-2023 по информатике

Канал видеоролика: Иван Викторович

Смотреть видео:

Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):

С этим видео ученики смотрят следующие ролики:

Разбор 16 задания на Python | ЕГЭ-2023 по информатике

Иван Викторович

Разбор 8 задания на Python | ЕГЭ-2023 по информатике

Иван Викторович

Разбор 12 задания на Python | ЕГЭ-2023 по информатике

Иван Викторович

Разбор 2 задания ЕГЭ по информатике решение в pascal и python (2019 вариант 4, Крылов С.С., Чуркина)

Светлана Майер

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

20.11.2022

Комментарии

RSS

Написать комментарий

Нет комментариев. Ваш будет первым!

Ваше имя:

Загрузка…

Источник

Kaztat37

6 / 5 / 1

Регистрация: 04.07.2021

Сообщений: 28

07.11.2021, 19:40. Показов 22281. Ответов 3

Метки егэ (Все метки)

(№ 4355) (П. Волгин) В файле 17-7.txt содержится последовательность целых чисел. Элементы последовательности могут принимать значения от 0 до 200 включительно. Определите сначала количество троек элементов последовательности, в которых хотя бы 2 числа из тройки в шестнадцатеричной системе счисления в нулевом разряде имеют 0, а затем сумму максимальных чисел из таких троек. Под тройкой подразумевается три идущих подряд элемента последовательности.

Python

f = open('C:/ЕГЭ/Информатика/Папка для временных заданий с вариантов/Задание №17/17.txt')
m, k, s = [int(x) for x in f], 0, 0
for i in range(len(m) - 2):
    if (((hex(m[i])[2:][-1] == '0') and (hex(m[i + 1])[2:][-1] == '0')) or
            ((hex(m[i])[2:][-1] == '0') and (hex(m[i + 2])[2:][-1] == '0')) or
            ((hex(m[i + 1])[2:][-1] == '0') and (hex(m[i + 2])[2:][-1] == '0')) or
            ((hex(m[i])[2:][-1] == '0') and (hex(m[i + 1])[2:][-1] == '0') and (hex(m[i + 2])[2:][-1] == '0'))):
        k += 1
        s = max(s, m[i] + m[i + 1] + m[i + 2])
print(k, s)

Мой ответ: 8 280
Правильный ответ: 8 1060

Вложения

17.txt (623 байт, 56 просмотров)

__________________
Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь

Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782	07.11.2021, 19:40
3

Gdez

6989 / 3910 / 1745

Регистрация: 27.03.2020

Сообщений: 6,722

07.11.2021, 20:15

Сообщение было отмечено Kaztat37 как решение

Решение

Kaztat37,

Python

def fun(a):
    return sum(i%16 == 0 for i in a)
    
    
with open('input1.txt') as fil:
    f = fil.read().splitlines()
m, k, s = [int(x) for x in f], 0, 0
 
for i in range(len(m) - 2):
    if fun(m[i:i+3]) == 2:
        k += 1
        s += max(m[i:i+3])
print(k, s)

Добавлено через 8 минут
«…не менее 2…»

Python

def fun(a):
    return sum(i%16 == 0 for i in a) > 1
    
    
with open('input1.txt') as fil:
    f = fil.read().splitlines()
m, k, s = [int(x) for x in f], 0, 0
 
for i in range(len(m) - 2):
    if fun(m[i:i+3]):
        k += 1
        s += max(m[i:i+3])
print(k, s)

anton78spb

950 / 567 / 265

Регистрация: 05.09.2021

Сообщений: 1,011

07.11.2021, 20:33

Сообщение было отмечено Kaztat37 как решение

Решение

Kaztat37, Вот готовый вариант. Исправил ошибку.

Python

with open('17.txt', 'r') as f:
    a = [int(line) for line in f]
 
b = [max(a[i: i + 3]) for i in range(len(a) - 2) if (a[i] % 16 == 0 and a[i + 1] % 16 == 0) 
     or (a[i] % 16 == 0 and a[i + 2] % 16 == 0) or (a[i + 1] % 16 == 0 and a[i + 2] % 16 == 0)]
 
print(len(b), sum(b))

Получилось 8 1060.

Gdez

6989 / 3910 / 1745

Регистрация: 27.03.2020

Сообщений: 6,722

07.11.2021, 20:34

Сообщение было отмечено Kaztat37 как решение

Решение

Kaztat37, если чисел много, то можно и так:

Python

with open('input1.txt') as fil:
    f = fil.read().splitlines()
cnt = s = 0
a, b, c = int(f[0]), int(f[1]), None
k = (a%16 == 0) + (b%16 == 0)
for i in range(2, len(f) - 2):
    c = int(f[i])
    k += (c%16 == 0)
    if k > 1:
        s += max(a,b,c)
        cnt+= 1
    k -= (a%16 == 0)
    a, b = b, c
print(cnt, s)

IT_Exp

Эксперт

87844 / 49110 / 22898

Регистрация: 17.06.2006

Сообщений: 92,604

07.11.2021, 20:34

Помогаю со студенческими работами здесь

Задача замутить бекап сайта на сторонний FTP
Здравствуйте! Была задача замутить бекап сайта на сторонний ФТП. Написал скрипт, но он выполняется…

Задача с сайта acm.timus про картины
Помогите решить , пожалуйста
Художник Иванов (не тот Иванов, который написал «Явление Христа…

Поиск подмассива в массиве (задача с сайта openedu)
Никак не получается решить задачу на сайте, выдает ошибку(
Проверял код в Visual Studio 2019 -…

задача зайчики с сайта acmp .можете посмотреть в чём ошибка?
#include <bits/stdc++.h>

using namespace std;

int count(int k, int n) {
++n;
…

Интересная задача с сайта lisp.ru: заменить в списке положительные числа ближайшим отрицательным (справа или слева)
Дан одноуровневый числовой список. Нужно заменить каждое положительное число ближайшим…

Почему папка сайта на денвере, находится у меня в корне сайта на хостинге ?
Привет всем, подскажите пожалуйста, правильно ли то, что у меня на сайте, в корне вой папке…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!

В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.

Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.

Всех желающих — приглашаю ниже!

Быстрый перевод из системы в систему

В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:

bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'

Вывод в интерпретационном режиме

Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…

Давайте посмотрим и на них:

n = int(input()) #Вводим целое число
 
b = '' #Формируем пустую строку
 
while n > 0: #Пока число не ноль
    b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
    n = n // 2 #Целочисленное деление
 
print(b) #Вывод

Данная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:

n = int(input()) #Вводим целое число

b = '' #Формируем пустую строку

while n > 0: #Пока число не ноль
	if (n % 21) > 9: #Если остаток от деления больше 9...
		if n % 21 == 10: #... и равен 10...
			b = 'A' + b #... запишем слева A
		elif n % 21 == 11:#... и равен 11...
			b = 'B' + b#... запишем слева B

'''

И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)

'''

		elif n % 21 == 11:
			b = 'B' + b
		elif n % 21 == 12:
			b = 'C' + b
		elif n % 21 == 13:
			b = 'D' + b
		elif n % 21 == 14:
			b = 'E' + b
		elif n % 21 == 15:
			b = 'F' + b
		elif n % 21 == 16:
			b = 'G' + b
		elif n % 21 == 17:
			b = 'H' + b
		elif n % 21 == 18:
			b = 'I' + b
		elif n % 21 == 19:
			b = 'J' + b
		elif n % 21 == 20:
			b = 'K' + b
	else: #Иначе (остаток меньше 10)
		b = str(n % 21) + b #Остатот от деления записываем слева
	n = n // 21 #Целочисленное деление

print(b) #Вывод

Способ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:

def convert_base(num, to_base=10, from_base=10):
    # Перевод в десятичную систему
    if isinstance(num, str): # Если число - строка, то ...
        n = int(num, from_base) # ... переводим его в нужную систему счисления
    else: # Если же ввели число, то ...
        n = int(num) # ... просто воспринять его как число
    # Перевод десятичной в 'to_base' систему
    alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
    if n < to_base: # Если число меньше системы счисления в которую переводить...
        return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
    else: # Иначе...
        return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остатка

Вызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).

Задача 2

Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.

Решение данной задачи совсем простое: банальный перебор.

print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
	for x in range(2):
		for z in range(2):
			for w in range(2):
				F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
				print(x, y, z, F) #Выводим результат

Результат:

Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:

print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
	for x in range(2):
		for z in range(2):
			for w in range(2):
				F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
				if not F:
					print(x, y, z, F) #Выводим результат

Результат:

Далее — простой анализ.

Задача 5

Данная задача легко решается простой последовательностью действий в интерпретационном режиме:

Задача 6

Перепечатали и получили ответ:

s = 0
k = 1
while s < 66:
    k += 3
    s += k
print(k)

Задача 12

В очередной раз, просто заменим слова на код:

a = '9' * 1000

while '999' in a or '888' in a:
	if '888' in a:
		a = a.replace('888', '9', 1)
	else:
		a = a.replace('999', '8', 1)
print(a)

Задача 14

Компьютер железный, он всё посчитает:

a = 4 ** 2020 + 2 ** 2017 - 15
k = 0

while a > 0:
    if a % 2 == 1:
    	k += 1
    a = a // 2

print(k)

Задача 16

Опять же, просто дублируем программу в python:

def F(n):
    if n > 0:
        F(n // 4)
        print(n)
        F (n - 1)
print(F(5))

Результат:

Задача 17

Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!

with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
    text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)

k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...

for i in range(len(a)): #Обходим все элементы массива
	if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
		k += 1 #Счётчик
		if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
			m = int(a[i - 1]) + int(a[i])

print(k, m) #Вывод

Немного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.

Задача 19, 20 и 21

Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:

Пишем рекурсивную функцию и цикл перебора S:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 3: #Условия завершения игры
		return p == 3
	return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
		   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий

for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)
		break

Немного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:

	Игра	Петя	Ваня	Петя	Ваня	Петя
p	1	2	3	4	5	6

Далее — всё по условию задачи.

Вторая задача на теорию игр:

Все отличия в рамке. Ну и код, соответственно, не сильно отличается:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 4: #Условия завершения игры
		return p == 4
	if p % 2 != 0:
		return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
			   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
	else:
		return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
			   f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий


for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)

Отличия:

Выиграл Петя, соответственно, позиция 4
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
Убрали break, так как нам нужны все S, а не единственный

Последняя вариация задачи:

Сразу код:

def f(x, y, p): #Рекурсивная функция
	if x + y >= 69 or p > 5: #Условия завершения игры
		return p == 3 or p == 5
	if p % 2 == 0:
		return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
			   f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
	else:
		return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
			   f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий


for s in range (1, 58 + 1): #Перебор S
	if f(10, s, 1): #Начали с 10 камней
		print(s)

Ну и всего лишь 2 отличия:

Позиции 3 или 5, а не 4, так как выиграл Ваня
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.

Задача 22

Ctrl+C, Ctrl+V — наше всё!

for i in range(1, 100000):
	x = i
	L = 0
	M = 0
	while x > 0 :
		L = L+1
		if (x % 2) != 0:
			M = M + x % 8
		x = x // 8
	if L == 3 and M == 6:
		print(i)

Задача 23

Итак, код:

def f(x, y):
	if x > y: #Перегнали цель
		return 0
	if x == y:  #Догнали цель
		return 1
	if x < y: #Догоняем цель тремя методами
		return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)

print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12

Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.

Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.

Ссылка на репозиторий со всеми программами:

Надеюсь, что смог помочь в своей статье выпускникам и готовящимся

Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.

Всем удачи!

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

Делаю разбор второй части?

Проголосовали 106 пользователей.

Воздержались 15 пользователей.

Источник