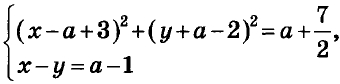Решение и ответы заданий Варианта №18 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
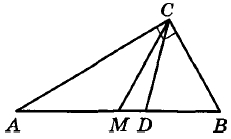
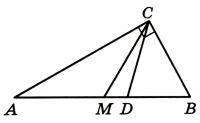
Угол между биссектрисой CD и медианой СМ проведёнными из вершины прямого угла С треугольника АВС, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задание 2.
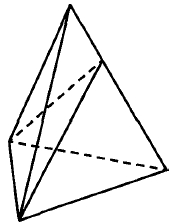
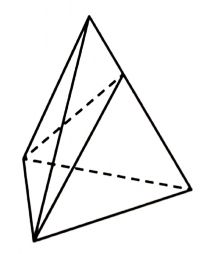
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Задание 3.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России.
Задание 4.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Задание 5.
Найдите корень уравнения log4 25x+7 = 3.
Задание 6.
Найдите значение выражения frac{a^{3,33}}{ a^{2,11}cdot a^{2,22}} при а = frac{2}{7}.
Задание 7.
Прямая у = 9х + 6 является касательной к графику функции у = ах2 – 19х + 13. Найдите а.
Задание 8.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 километра. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Задание 9.
Первый садовый насос перекачивает 10 литров воды за 5 минут, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литра воды?
Задание 10.
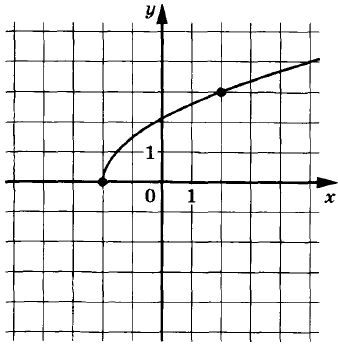
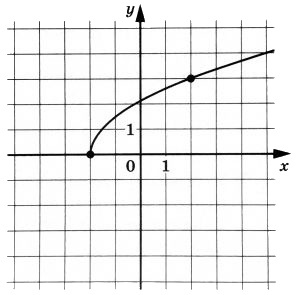
На рисунке изображён график функции f(x) = ksqrt{x+p}. Найдите f(0,25).
Задание 11.
Найдите наибольшее значение функции у = 2х2 – 12х + 8lnх – 5 на отрезке [frac{12}{13};frac{14}{13}].
Задание 12.
а) Решите уравнение 7cosx – 4cos3x = 2√3sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; –3π].
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.
Задание 14.
Решите неравенство log52(x4) – 28log0,04 (x2) ≤ 8.
Задание 15.
Производство х тыс. единиц продукции обходится в q = 3х2 + 6х + 13 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<3.
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{5}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{8}]+[frac{n}{23}]=n+2021?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень уравнения (log_4{2^{5x+7}}=3).
Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).
Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).
Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).
а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.
Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).
Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2}, \ x-y=a-1 end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Задание 1
Найдите корень уравнения $$(frac{1}{5})^{3x+5}=0,04.$$
Ответ: -1
Скрыть
$$(frac{1}{5})^{3x+5}=0,04$$
$$(frac{1}{5})^{3x+5}=frac{1}{25}$$
$$(frac{1}{5})^{3x+5}=(frac{1}{5})^2$$
$$3x+5=2$$
$$3x=2-5$$
$$3x=-3$$
$$x=-1$$
Задание 2
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно один раз.
Ответ: 0,375
Скрыть
Для более наглядного представления распишем все возможные комбинации выпадения орла и решки при трехкратном подбрасывании монеты (О — орел, Р — решка):
1) О, О, О,
2) Р, Р, Р,
3) Р, Р, О (*),
4) Р, О, Р (*),
5) О, Р, Р (*),
6) Р, О, О,
7) О, Р, О,

Всего вышло 8 вариантов. Из них орел выпадает ровно один раз — 3 варианта. Значит, вероятность выпадения орла один раз равна $$frac{3}{8}=0,375.$$
Задание 3
Радиус окружности, описанной около треугольника АВС, равен $$2sqrt{3}.$$ Найдите АВ, если угол АСВ равен $$120^{circ}.$$
Ответ: 6
Скрыть
Воспользуемся расширенной теоремой синусов, которую можно записать в виде:
$$frac{AB}{sinangle C}=2R$$
откуда
$$AB=2Rcdotsinangle C$$
$$AB=2cdot2sqrt{3}cdotsin120=2cdot2sqrt{3}cdotfrac{sqrt{3}}{2}=6$$
Задание 4
Найдите значение выражения $$2sqrt{6}cosfrac{pi}{4}sinfrac{7pi}{6}tan(-frac{2pi}{3}).$$
Ответ: -3
Скрыть
$$2sqrt{6}cosfrac{pi}{4}sinfrac{7pi}{6}tan(-frac{2pi}{3})=2sqrt{6}cdotfrac{sqrt{2}}{2}cdot(-frac{1}{2})cdotsqrt{3}=$$
$$=-frac{2cdotsqrt{36}}{2cdot2}=-frac{6}{2}=-3$$
Задание 5
В сосуд, имеющий форму правильной треугольной призмы, налили 1100 $$см^3$$ воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 29 см. Чему равен объём детали? Ответ выразите в $$см^3.$$
Ответ: 176
Скрыть
При погружении детали в жидкость, высота жидкости изменилась на
$$Delta h=29-25=4$$ см
Учитывая, что площадь основания призмы не менялась, то изменение объема можно записать как
$$Delta V=Delta hcdot S_{осн}$$
где
$$S_{осн}=frac{V_1}{h_1}=frac{1100}{25}=44$$
Получаем объем детали:
$$Delta=4cdot44=176$$
Задание 6
На рисунке изображён график $$у=f'(x)$$ — производной функции $$f(x),$$ определённой на интервале $$(-8; 3).$$ В какой точке отрезка $$[-5; 0]$$ функция $$f(x)$$ принимает наибольшее значение?
Ответ: -3
Скрыть
Известно, что производная положительная в окрестностях точек, где функция возрастает и отрицательная, где функция убывает. Анализ графика производной показывает, что на участке $$[-5; -3]$$ функция $$f(x)$$ возрастала, а затем, на участке $$[-3; 0]$$ – убывала. Следовательно, максимальное значение она приобретает в точке $$-3.$$
Задание 7
Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Ор и объективности Tr публикаций, а также качества Q сайта. Каждый отдельный показатель — целое число от 0 до 4. Составители рейтинга считают, что информативность публикаций ценится вдвое, а объективность — втрое дороже, чем оперативность и качество сайта, то есть
$$R=frac{2In+Op+3Tr+Q}{A}.$$
Найдите, каким должно быть число А, чтобы издание, у которого все показатели максимальны, получило рейтинг 1.
Ответ: 28
Скрыть
Выразим из формулы рейтинга величину A, получим:
$$A=frac{2In+Op+3Tr+Q}{R}$$
Подставим сюда максимальные значения $$4$$ и $$R=1,$$ получим величину A:
$$A=frac{2cdot4+4+3cdot4+4}{1}=28$$
Задание 8
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 36 км. Путь из А в В занял у туриста 10 часов, из которых 2 часа ушло на спуск.
Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
Ответ: 6
Скрыть
Пусть $$x$$ км/ч – скорость туриста на спуске. Тогда скорость на подъеме $$x-3$$ км/ч. В задании сказано, что на спуск ушло $$t_1=2$$ часа, значит, на подъем $$t_2=10-2=8$$ часов. Получаем общий пройденный путь:
$$2cdot x+8cdot(x-3)=36$$
$$2x+8x-24=36$$
$$10x=60$$
$$x=6$$
Задание 9
На рисунке изображён график функции $$f(x)=a^x+b.$$ Найдите, при каком значении $$x$$ значение функции равно $$33.$$
Ответ: -5
Скрыть
Точки A(0;2) и B(-1;3) принадлежат графику функции. Получили:
$$left{begin{matrix} 2=a^0+b\ 3=a^{-1}+b end{matrix}right.Leftrightarrowleft{begin{matrix} 2=1+b\ a^{-1}=3-b end{matrix}right.Leftrightarrowleft{begin{matrix} b=1\ a^{-1}=2 end{matrix}right.Leftrightarrowleft{begin{matrix} b=1\ a=frac{1}{2} end{matrix}right.$$
Получили:
$$(frac{1}{2})^x+1=33Leftrightarrow(frac{1}{2})^x=32=(frac{1}{2})^{-5}Leftrightarrow x=-5$$
Задание 10
По отзывам покупателей Пётр Петрович оценил надёжность двух интернет- магазинов. Вероятность того, что нужный товар доставят вовремя из магазина А, равна 0,92. Вероятность того, что этот товар доставят вовремя из магазина Б, равна 0,85. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
Ответ: 0,012
Задание 11
Найдите наибольшее значение функции $$у=7ln(х+5)-7х+10$$ на отрезке $$[-4,5; 0].$$
Ответ: 38
Скрыть
$$у=7ln(х+5)-7х+10$$
Найдём производную функции:
$$y’=7cdot{1}{x+5}-7$$
Найдём нули производной:
$$7cdot{1}{x+5}-7=0$$
$$7cdot{1}{x+5}=7$$
$$frac{1}{x+5}=1$$
$$x+5=1$$
$$x=1-5=-4$$
Определим знаки производной функции и изобразим её поведение:
Точка максимума $$x=-4,$$ там и будет максимальное значение функции:
$$y(-4)=7ln(-4+5)-7cdot(-4)+10=7cdot0+28+10=38$$
Задание 12
а) Решите уравнение $$cos 2x-sin 2x=cos x+sin x+1.$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi].$$
Ответ: $$а) -frac{pi}{4}+pi k,-frac{pi}{6}+2pi k,-frac{-5pi}{6}+2pi k, kin Z;$$ $$б) -frac{9pi}{4};-frac{13pi}{6};-frac{5pi}{4}$$
Скрыть
а) Решите уравнение
$$cos 2x-sin 2x=cos x+sin x+1$$
ОДЗ уравнения: R
Используя формулу косинуса двойного угла $$cos 2alpha=cos^2 alpha–sin^2 alpha,$$ формулу синуса двойного угла $$sin 2alpha=2sin alphacos alpha,$$ основное тригонометрическое тождество $$cos^2 alpha+sin^2 alpha=1,$$ преобразуем уравнение:
Используя формулу косинуса двойного угла $$cos 2alpha=cos^2 alpha-sin^2 alpha,$$ формулу синуса двойного угла $$sin 2alpha=2sinalphacosalpha,$$ основное тригонометрическое тождество $$cos^2alpha+sin^2alpha=1,$$ преобразуем уравнение:
$$cos^2 x-sin^2 x-2sin xcos x=cos x+sin x+cos^2 x+sin^2 x$$
$$cos^2 x-sin^2 x-2sin xcos x-cos x-sin x-cos^2 x-sin^2 x=0$$
$$-2sin^2 x-2sin xcos x-cos x-sin x=0$$
$$2sin^2 x+2sin xcos x+cos x+sin x=0$$
Воспользуемся методом группировки:
$$(2sin^2 x+2sin xcos x)+(cos x+sin x)=0$$
$$2sin x(sin x+cos x)+(sin x+cos x)=0$$
$$(sin x+cos x)cdot(2sin x+1)=0$$
Уравнение состоит из двух множителей. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла, т. е.
$$sin x+cos x=0$$ или $$2sin x+1=0$$
Решим первое уравнение:
$$sin x+cos x=0$$
Получили однородное тригонометрическое уравнение первой степени. Так как $$sin x$$ и $$cos x$$ обращаются в нуль в различных точках, т. е. не могут быть одновременно равными нулю, то можно обе части уравнения разделить на $$cos x:$$
$$frac{sin x}{cos x}+frac{cos x}{cos x}=frac{0}{cos x}$$
$$tan x+1=0$$
$$tan x=-1$$
$$x=arctan(-1)+pi n,nin Z$$
$$x=-frac{pi}{4}+pi n,nin Z$$
Решим второе уравнение:
$$2sin x+1=0$$
$$sin x=-frac{1}{2}$$
$$x=-frac{pi}{6}+2pi m, min Z$$ и $$x=-frac{5pi}{6}+2pi k, kin Z$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2}; -pi].$$
Выберем корни уравнения при помощи единичной окружности
$$x=-frac{9pi}{4};-frac{13pi}{6};-frac{5pi}{4}$$
Задание 13
В правильной четырёхугольной призме $$ABCDA_1B_1C_1D_1$$ сторона основания $$АВ$$ равна $$3,$$ а боковое ребро $$АА_1$$ равно $$sqrt{3}.$$ На рёбрах $$C_1D_1$$ и $$DD_1$$ отмечены соответственно точки $$К$$ и $$М$$ так, что $$D_1K=KC_1,$$ a $$DM:MD_1=1:3.$$
а) Докажите, что прямые $$МК$$ и $$ВК$$ перпендикулярны.
б) Найдите угол между плоскостями $$ВМК$$ и $$ABB_1.$$
Ответ: $$arctgfrac{2sqrt{21}}{7}$$
Скрыть
а)
$$DM=frac{sqrt{3}}{4}$$
$$D_1M=frac{3sqrt{3}}{4}$$
$$BC_1=sqrt{12}$$ (т. Пифагора)
$$MK=frac{3sqrt{7}}{4}$$ (т. Пифагора)
$$DB=3sqrt{2}$$ (свойство квадратов)
$$BM=sqrt{18+frac{3}{16}}=frac{sqrt{291}}{4}$$ (т. Пифагора)
$$BK=sqrt{frac{9}{4}+12}=frac{sqrt{57}}{2}$$ (т. Пифагора)
Сравним $$BM^2$$ и $$MK^2+BK^2$$
$$frac{291}{16}$$ и $$frac{63}{16}+frac{57}{4}$$
$$BM^2=MK^2+BK^2$$
По теореме, обратной теореме косинусов вывод:
$$MKperp BK, чтд$$
б)
$$(ABB_1)||(DD_1C_1)$$
Найдём $$widehat{(DD_1C_1)(MKB)},$$ он равен искомому.
Д. П. $$KNperp MK$$
$$ctgalpha=tg(90^{circ}-alpha)=frac{2}{sqrt{3}}$$
Треугольник $$KC_1N:$$
$$C_1N=frac{3}{2}cdotfrac{2}{sqrt{3}}=sqrt{3}$$
$$Rightarrow$$ т. N совпадает с т. C.$$Rightarrow CKperp MK$$
$$angle BKC=x$$ — искомый (по определению)
Треугольник $$KC_1C:$$
$$KC=sqrt{frac{9}{4}+3}=frac{sqrt{21}}{2}$$ (по т. Пифагора)
Треугольник $$BKC:$$
$$tgx=frac{3}{frac{sqrt{21}}{2}}=frac{6}{sqrt{21}}=frac{6sqrt{21}}{21}=frac{2sqrt{21}}{7}$$
$$x=arctgfrac{2sqrt{21}}{7}$$
Задание 14
Решите неравенство $$lg^4(x^2-4)^2-lg^2(x^2-4)^4geq192.$$
Ответ: $$(-infty;-2sqrt{26}];[-sqrt{4,01};-2);(-2;-sqrt{3,99}];[sqrt{3,99};2);(2;sqrt{4,01}];[2sqrt{26};+infty)$$
Скрыть
$$lg^4(x^2-4)^2-lg^2(x^2-4)^4geq192$$
ОДЗ: $$xneqpm2$$
$$16lg^4|x^2-4|-16lg^2|x^2-4|geq192$$
$$lg^2|x^2-4|=tgeq0$$
$$left{begin{matrix} tgeq0\ t^2-t-12geq0 end{matrix}right.left{begin{matrix} tgeq0\ tgeq4 end{matrix}right.$$
Переход к старой переменной:
$$lg^2|x^2-4|geq0$$
$$(lg |x^2-4|leq-2)(lg |x^2-4|leq-2)geq0$$
$$left[begin{matrix} lg|x^2-4|leq-2\ lg|x^2-4|geq2 end{matrix}right.left[begin{matrix} |x^2-4|leq0,1 (1)\ |x^2-4|geq100 (2) end{matrix}right.$$
(1) $$left{begin{matrix} x^2-4leq0,01\ x^2-4geq-0,01 end{matrix}right.left{begin{matrix} (x-sqrt{4,01})(x+sqrt{4,01})leq0\ (x-sqrt{3,99})(x+sqrt{3,99})geq0 end{matrix}right.left{begin{matrix} xin[-sqrt{4,01};sqrt{4,01}]\ xin(-infty;-sqrt{3,99}];[sqrt{3,99};+infty) end{matrix}right.$$
$$xin [-sqrt{4,01};-sqrt{3,99}]cup[sqrt{3,99};sqrt{4,01}]$$
(2) $$left[begin{matrix} (x-2sqrt{26})(x+2sqrt{26})geq0\ x^2-4leq-100 end{matrix}right.$$
$$xin(-infty;-2sqrt{26}];[-sqrt{4,01};-2);(-2;-sqrt{3,99}];[sqrt{3,99};2);(2;sqrt{4,01}];[2sqrt{26};+infty)$$
Задание 15
Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Ответ: 78 125 рублей
Скрыть
Пусть Сергей в середине каждого месяца откладывает $$x$$ рублей
Тогда к середине $$n-го$$ месяца у Александра будет $$ncdot x$$ рублей, а акции будут стоить, по условию, не более $$160000cdot1,25^{n−1}$$
Для того, чтобы Сергей смог купить акции должно быть выполнено неравенство:
$$xgeqfrac{160000cdot1,25^{n−1}}{n}$$
Пусть $$an=frac{1,25^{n−1}}{n}$$
Нам нужно найти наименьшее из чисел $$an.$$ Найдем когда последовательность убывает, для этого
Сравним $$frac{a_{n+1}}{a_n}leq1$$
$$frac{a_{n+1}}{a_n}=frac{5n}{4(n+1)}leq1$$
$$nleq4$$
Тогда наименьший элемент последовательности равен $$a_4=frac{125}{256}$$
Тогда
$$x=160000cdotfrac{125}{256}=78125$$
Задание 16
На сторонах АС, АВ и ВС прямоугольного треугольника АВС с прямым углом С вне треугольника АВС построены равнобедренные прямоугольные треугольники АКС, ALB и ВМС с прямыми углами К, L и М соответственно.
а) Докажите, что LC — высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC = 6.
Ответ: 18
Скрыть
а) Рассмотрим четырехугольник ALBC, у которого углы $$ACB=ALB=90^{circ},$$ а значит, вокруг него можно описать окружность (по свойству: сумма противоположных углов $$ACB+ALB=180^{circ}$$). Тогда хорды AL = LB (треугольники АКС, ALB и ВМС – равнобедренные) стягивают дуги $$cup AL=cup LB,$$ следовательно, вписанные углы, опирающиеся на эти дуги, также равны: $$angle ACL=angle LCB=45^{circ};$$ $$angle KCA+angle ACL=45^{circ}+45^{circ}=90^{circ};$$ $$angle LCB+angle BCM=90^{circ},$$ следовательно, LC перпендикулярна KM и LC – высота треугольника KLM.
б) Площадь треугольника KLM можно найти по формуле:
$$S_{KLM}=frac{1}{2}KMcdot LC$$
Пусть BC = a, AC = b, CL = d, AB = c, а P – точка пересечения AB и CL. Так как $$angle ACP=angle BCP=45^{circ},$$ то CB – биссектриса треугольника ABC. По свойству биссектрис:
$$frac{AP}{PB}=frac{AC}{CB}=frac{b}{a}$$
Учитывая, что AP + PB = AB = c, получаем систему:
$$frac{AP}{PB}=frac{b}{a}$$
$$AP+PB=c$$
С решением:
$$AP=frac{bc}{a+b}; PB=frac{ac}{a+b}$$
Так как углы $$angle ACL=angle BAL=45^{circ},$$ то треугольники ACL и PAL подобны по двум углам и:
$$frac{AC}{PA}=frac{CL}{AL}Rightarrow b: frac{bc}{a+b}=d:frac{c}{sqrt{2}}$$
и $$d=frac{a+b}{sqrt{2}}.$$ Из равенства KM = KC + CM, получаем:
$$KM=frac{a}{sqrt{2}}+frac{b}{sqrt{2}}=d=6$$
Следовательно:
$$S_{KLM}=frac{1}{2}cdot6cdot6=18$$
Задание 17
Найдите, при каких неположительных значениях а функция $$f(x)= ax^4+4x^3-3x^2-5$$ на отрезке [-2; 2] имеет две точки максимума.
Ответ: $$(-frac{3}{2}; -frac{9}{8}]$$
Скрыть
Найдем производную заданной функции: $$f'(x)=4ax^3+12x^2-6x.$$ Необходимо и достаточно, чтобы f’ имела на отрезке [−2; 2] два нуля, в которых она меняет знак с плюса на минус. При этом, если корней ровно два, то в одном из них производная знак не меняет. Следовательно, корней ровно три и характеры смены знака в них чередуются (с плюса на минус, с минуса на плюс и снова с плюса на минус). Поэтому все три корня должны лежать на отрезке [−2; 2]. Тогда
$$4ax^3+12x^2-6x=0Leftrightarrow 2x(2ax^2+6x-3)=0.$$
Следовательно, число $$x=0$$ — корень, то есть теперь необходимо и достаточно, чтобы два корня уравнения $$2ax^2+6x-3=0$$ лежали на отрезке [−2; 2].
Учитывая, что графиком функции $$g(x)=2ax^2+6x-3$$ при $$a<0$$ является парабола, ветви которой направлены вниз, необходимо и достаточно выполнения системы неравенств:
$$left{begin{matrix} g(2)leq0,\ g(-2)leq0,\ D>0,\ x_{верш}in(-2;2), end{matrix}right.$$
то есть
$$left{begin{matrix} 8a+12-3leq0,\ 8a-12-3leq0,\ 36+24a>0,\ -2<-frac{6}{4a}<2 end{matrix}right.Leftrightarrow left{begin{matrix} aleq-frac{9}{8},\ aleqfrac{15}{8},\ a>-frac{3}{2},\ a>-frac{3}{4} end{matrix}right.Leftrightarrow aleq-frac{9}{8}.$$
Задание 18
Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1).
а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 10 нулями?
б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 17 нулями?
в) Сколько существует натуральных чисел n, меньших 75, для каждого из которых десятичная запись числа $$n! cdot (75 — n)!$$ оканчивается ровно 17 нулями?
Ответ: а) да; б) нет; в) 12
Скрыть
Раскладывая все числа от 1 до n на простые множители и объединяя затем множители 2 и 5 в пары, мы будем получать множители 10, которые просто прибавляют 0 на конце числа. Когда множители 2 или 5 (на самом деле всегда 5) закончатся, оставшееся число не будет кончаться на 0, поэтому количество нулей равно либо суммарному количеству пятерок, либо суммарному количеству двоек в разложении всех чисел от 1 до n на простые множители.
а) Пусть n = 45. Есть ровно 9 чисел кратных 5 от 1 до 45, при этом одно (25) содержит сразу две пятерки. Ясно, что 10 двоек наберется (там есть 22 четных числа, дающих минимум по одной двойке).
б) Среди чисел 1, 2, …, 74 есть 14 кратных 5, из них 25, 50 кратны 52. Значит, 74! оканчивается на (14 − 2) + 2 · 2 = 16 нулей. При этом 75! = 74! · 75 окачивается на 18 нулей. Ясно, что при n < 74 число нулей будет не более 16, а при n > 75 — не менее 18.
в) Среди чисел от 1 до n ровно $$left[frac{n}{5}right]$$ кратны 5 и ровно $$left[frac{n}{25}right]$$ кратны 25, поэтому степень пятерки в n! равна $$left[frac{n}{5}right]-left[frac{n}{25}right]+2cdotleft[frac{n}{25}right]=left[frac{n}{5}right]+left[frac{n}{25}right]$$ (здесь используется, что n ≤ 75, то есть числа, кратные 53, 54, …, отсутствуют). Тогда в записи n! · (75 − n)! ровно
$$left[frac{n}{5}right]+left[frac{75-n}{5}right]+left[frac{n}{25}right]+left[frac{75-n}{25}right]=left[frac{n}{5}right]+left[15-frac{n}{5}right]+left[frac{n}{25}right]+left[3-frac{n}{25}right]$$
нулей. Заметим, что при целом k [α] + [k − α] = k при целом α и [α] + [k − α] = k − 1 при нецелом α, поэтому $$left[frac{n}{5}right]+left[15-frac{n}{5}right]=15$$ или $$14$$ и $$left[frac{n}{25}right]+left[3-frac{n}{25}right]=3$$ или $$2.$$ Нас интересует вариант 15 + 2 (вариант 14 + 3 означал бы, что n не кратно 5, но кратно 25, что невозможно). Значит, n кратно 5, но не 25. Таких чисел 12.
Отметим, что одно из чисел n или 100 − n не меньше 38, поэтому его факториал содержит не менее 19 четных множителей, так что двоек на все эти пятерки хватит.
| 3244 | В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt3. На ребрах C1D1 и DD1 отмечены соответственно точки K и M так, что D1K=KC1, а DM:MD1=1:3. а) Докажите, что прямые MK и BK перпендикулярны. б) Найдите угол между плоскостями BMK и ABB1 |
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt 3 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 13 # Задача-аналог 2574 | |
| 3243 | В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно один раз |
Найдите вероятность того, что орёл выпадет ровно один раз ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 2 | |
| 3242 | Радиус окружности, описанной около треугольника ABC, равен 2sqrt3. Найдите AB, если угол ACB равен 120 гр |
Радиус окружности, описанной около треугольника ABC, равен 2 корня из 3 ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 3 | |
| 3241 | Найдите значение выражения 2sqrt(6)*cos(pi/4)*sin((7pi)/6)*tan(-(2pi)/3) |
Найдите значение выражения 2 корня из 6 cos pi/4 sin 7pi/6 tg -2pi/3 ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 4 | |
| 3240 | В сосуд, имеющий форму правильной треугольной призмы, налили 1100 см3 воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 29 см. Чему равен объём детали? Ответ выразите в см3 |
В сосуд, имеющий форму правильной треугольной призмы, налили воды и полностью в неё погрузили деталь ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 5 | |
| 3239 | Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 36 км. Путь из А в В занял у туриста 10 часов, из которых 2 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч |
Дорога между пунктами А и В состоит из подъёма и спуска ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 8 | |
| 3238 | На рисунке изображён график функций f(x)=a^x+b. Найдите, при каком значении x значение функции равно 33
|
Найдите, при каком значении x значение функции равно 33 ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 9 | |
| 3237 | Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? |
Сергей хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 15 # Приведенорешениепрототипаcolor{blue} text{Приведено решение прототипа 2872}задачи- аналога 2872 | |
| 3236 | На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно. а) Докажите, что LC — высота треугольника KLM. б) Найдите площадь треугольника KLM, если LC=6 |
б) Найдите площадь треугольника KLM, если LC=6 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 16 # Приведенорешениепрототипаcolor{blue} text{Приведено решение прототипа 2573}задачи- аналога 2573 | |
| 2579 | Найдите наибольшее значение функции y=7ln(x+5)-7x+10 на отрезке [-4.5; 0] |
Найдите наибольшее значение функции y= 7ln(x+5) -7x +10 ! 36 вариантов ФИПИ Ященко 2022 Вариант 18 Задание 11 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 8 Задание 12 | |
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30
Ответы к пособию для подготовки ЕГЭ-2023 по математике. Профильный уровень. Типовые экзаменационные варианты. Под редакцией И. В. Ященко. 36 вариантов.
| Вариант 1 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 5.5 | 10 | -4 |
| 2 | 2048 | 11 | -2910 |
| 3 | 0.06 | 12 | 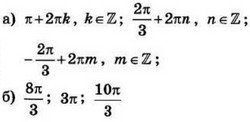 |
| 4 | 0.89 | 13 | б) 24 |
| 5 | -0.2 | 14 | 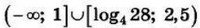 |
| 6 | 0.5 | 15 | 400 тыс. рублей |
| 7 | 5 | 16 | б) 14.2 |
| 8 | 5.832 | 17 | (-4; -3) ∪ (-3; -1) ∪ (-1; 0) |
| 9 | 2 | 18 | а) да; б) нет; в) 205 |
| Вариант 2 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 7.5 | 10 | -8 |
| 2 | 4 | 11 | 12.25 |
| 3 | 0.12 | 12 | 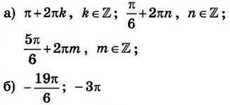 |
| 4 | 0.91 | 13 | б) 26 |
| 5 | -0.9 | 14 | 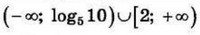 |
| 6 | 0.2 | 15 | 210 тыс. рублей |
| 7 | 1 | 16 | б) 29.7 |
| 8 | 0.216 | 17 | (0; 0.8) ∪ (0.8; 3.2) ∪ (3.2; 4) |
| 9 | 16 | 18 | а) да; б) нет; в) 195 |
| Вариант 3 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 32 |
| 2 | 30 | 11 | 204 |
| 3 | 0.37 | 12 | 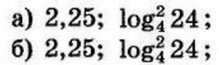 |
| 4 | 0.375 | 13 | б) 180 |
| 5 | -2.5 | 14 | 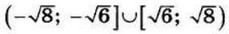 |
| 6 | 4 | 15 | 7.28 млн рублей |
| 7 | 2 | 16 | б) 32 |
| 8 | 51.2 | 17 | 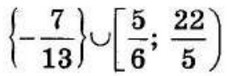 |
| 9 | 14 | 18 | а) да; б) да; в) 2295 |
| Вариант 4 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 1.5 | 10 | -56 |
| 2 | 12 | 11 | -10.9 |
| 3 | 0.24 | 12 |  |
| 4 | 0.125 | 13 | б) 40 |
| 5 | 0.375 | 14 | 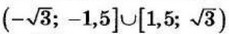 |
| 6 | 125 | 15 | 8 937 тыс. рублей |
| 7 | 8 | 16 | 42.16 |
| 8 | 281.25 | 17 | 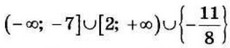 |
| 9 | 18 | 18 | а) да; б) нет; в) 897 |
| Вариант 5 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 99.5 | 10 | 16 |
| 2 | 12 | 11 | -52 |
| 3 | 0.004 или -0.004 | 12 | 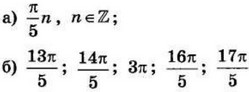 |
| 4 | 0.9409 | 13 | 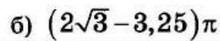 |
| 5 | -0.5 | 14 | 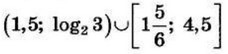 |
| 6 | 2 | 15 | 8.4 млн рублей |
| 7 | -19 | 16 | б) 9.1 |
| 8 | 60 | 17 | 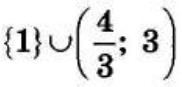 |
| 9 | 17 | 18 | а) нет; б) нет; в) 36 |
| Вариант 6 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 55 | 10 | -1 |
| 2 | 18 | 11 | -6 |
| 3 | 0.006 или -0.006 | 12 | 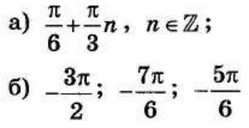 |
| 4 | 0.8464 | 13 | 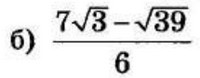 |
| 5 | -5.5 | 14 | 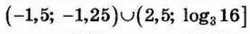 |
| 6 | 3 | 15 | 5.65 млн рублей |
| 7 | -4 | 16 | 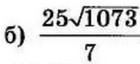 |
| 8 | 30 | 17 | 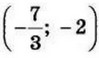 |
| 9 | 24 | 18 | а) нет; б) нет; в) 57, 58, 59, 60, 61 |
| Вариант 7 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.2 | 10 | 6 |
| 2 | 10 | 11 | 0.5 |
| 3 | 0.2 | 12 | 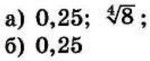 |
| 4 | 0.56 | 13 | б) 3 |
| 5 | -0.4 | 14 | 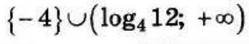 |
| 6 | -1 | 15 | 8 млн рублей |
| 7 | 9 | 16 | б) 6√2 |
| 8 | 0.6 | 17 | 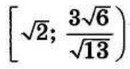 |
| 9 | 55 | 18 | а) да; б) нет; в) 79 |
| Вариант 8 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.4 | 10 | 0.25 |
| 2 | 5 | 11 | 17 |
| 3 | 0.125 | 12 | 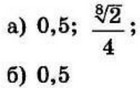 |
| 4 | 0.46 | 13 | 6√3 |
| 5 | -7 | 14 | 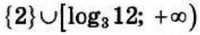 |
| 6 | -1 | 15 | 13 млн рублей |
| 7 | 7 | 16 | 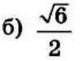 |
| 8 | 1.8 | 17 | 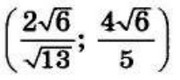 |
| 9 | 11 | 18 | а) да; б) нет; в) 73 |
| Вариант 9 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 3 | 10 | -3 |
| 2 | 15 625 | 11 | 9 |
| 3 | 0.01 | 12 | 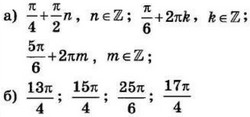 |
| 4 | 0.28 | 13 | 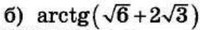 |
| 5 | -12 | 14 | (-∞; -1) |
| 6 | 144 | 15 | 7 млн рублей |
| 7 | -1 | 16 | 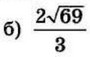 |
| 8 | 756 | 17 | 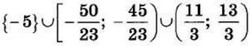 |
| 9 | 20 | 18 | а) да; б) нет; в) 176 |
| Вариант 10 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.6 | 10 | 253 |
| 2 | 150 | 11 | -23.25 |
| 3 | 0.28 | 12 | 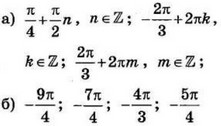 |
| 4 | 0.17 | 13 | 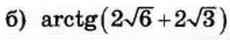 |
| 5 | -2.6 | 14 | (-∞; -2) |
| 6 | 625 | 15 | 4 млн рублей |
| 7 | -18 | 16 | 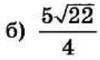 |
| 8 | 220.5 | 17 | 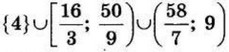 |
| 9 | 9 | 18 | а) нет; б) нет; в) 1933 |
| Вариант 11 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | -0.7 | 10 | 78 |
| 2 | 72 | 11 | 6.75 |
| 3 | 0.25 | 12 | 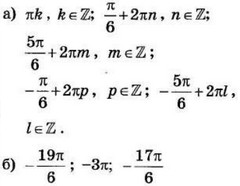 |
| 4 | 0.043 | 13 | б) 80√3 |
| 5 | -0.2 | 14 | (-∞; 0] ∪ [2; 3] |
| 6 | -5 | 15 | 600 тыс. рублей |
| 7 | -1 | 16 | 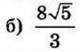 |
| 8 | 50 | 17 | {-5} ∪ (-1; 0) |
| 9 | 17.5 | 18 | а) да; б) нет; в) 97 |
| Вариант 12 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | -23 |
| 2 | 24 | 11 | 6.25 |
| 3 | 0.55 | 12 | 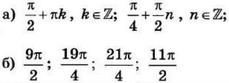 |
| 4 | 0.02 | 13 | б) 150 |
| 5 | -1.5 | 14 | (-∞; 0) ∪ (log53; 1) |
| 6 | -4 | 15 | 750 тыс. рублей |
| 7 | 4 | 16 | 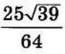 |
| 8 | 40 | 17 | 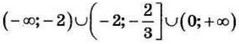 |
| 9 | 13.5 | 18 | а) да; б)нет; в) 85 |
| Вариант 13 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 8 | 10 | -0.5 |
| 2 | 48 | 11 | 77 |
| 3 | 0.4 | 12 | а) -2; -1 б) -1 |
| 4 | 0.6 | 13 | б) 5√3 |
| 5 | -9 | 14 | (1; 3] |
| 6 | 0.5 | 15 | 37 |
| 7 | 4 | 16 | б) 120/13 |
| 8 | 33 | 17 | [4√3; 12] |
| 9 | 9 | 18 | а) да; б) нет; в) 23/20 |
| Вариант 14 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 14 | 10 | 0.4 |
| 2 | 40.5 | 11 | 37 |
| 3 | 0.28 | 12 | 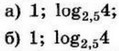 |
| 4 | 0.78 | 13 | 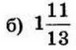 |
| 5 | -2 | 14 | [-3; -1) |
| 6 | 0.04 | 15 | 3 |
| 7 | 39 | 16 | б) 4 |
| 8 | 23 | 17 | 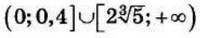 |
| 9 | 24 | 18 | 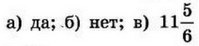 |
| Вариант 15 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 11.55 | 10 | 2.5 |
| 2 | 432 | 11 | 208 |
| 3 | 0.014 | 12 | 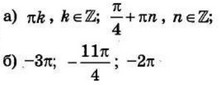 |
| 4 | 0.06 | 13 | 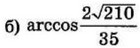 |
| 5 | -9 | 14 | (-1; 0) |
| 6 | 0.25 | 15 | 16 |
| 7 | 2 | 16 | б) 6 |
| 8 | 0.32 | 17 | 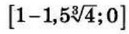 |
| 9 | 3 | 18 | а) да; б) нет; в) 26 |
| Вариант 16 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 12 | 10 | -15 |
| 2 | 192 | 11 | 5 |
| 3 | 0.29 | 12 | 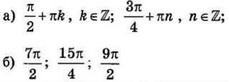 |
| 4 | 0.02 | 13 | 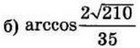 |
| 5 | -8 | 14 | (-∞; -0.5) |
| 6 | 0.125 | 15 | 19 |
| 7 | 4 | 16 | б) 8 |
| 8 | 1.16 | 17 | 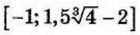 |
| 9 | 1 | 18 | а) да; б) нет; в) 80 |
| Вариант 17 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 10 | 10 | 16 |
| 2 | 80 | 11 | -24 |
| 3 | 0.08 | 12 | 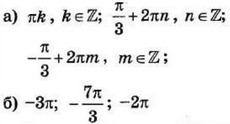 |
| 4 | 0.2 | 13 | б) 45° |
| 5 | -2.5 | 14 | 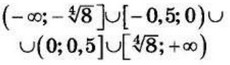 |
| 6 | 216 | 15 | 29 |
| 7 | -2 | 16 | б) 5/3 |
| 8 | 175 | 17 | -1/2; 2 |
| 9 | 18 | 18 | а) нет; б) да; в) 306 |
| Вариант 18 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | 2.25 |
| 2 | 10 | 11 | -15 |
| 3 | 0.2 | 12 | 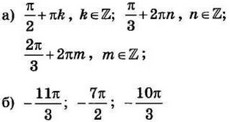 |
| 4 | 0.24 | 13 | б) arctg 0.5 |
| 5 | -0.2 | 14 | 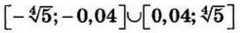 |
| 6 | 3.5 | 15 | 24 |
| 7 | 28 | 16 | б) 2.4 |
| 8 | 43.75 | 17 | 1; 9 |
| 9 | 21 | 18 | а) нет; б) да; в) 552 |
| Вариант 19 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 2 |
| 2 | 7.28 | 11 | -34 |
| 3 | 0.25 | 12 | 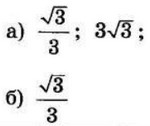 |
| 4 | 0.22 | 13 | б) 0.3√30 |
| 5 | -1.5 | 14 | (-∞; -1] ∪ [2; +∞) |
| 6 | 1 | 15 | 1300 тыс. рублей |
| 7 | 0.2 | 16 | б) 71° |
| 8 | 115 | 17 | 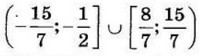 |
| 9 | 135 | 18 |  |
| Вариант 20 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | 27 |
| 2 | 7.68 | 11 | 0 |
| 3 | 0.75 | 12 | 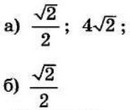 |
| 4 | 0.27 | 13 | б) arctg 2 |
| 5 | -4.5 | 14 | [-5; 0) ∪ (0; 2.5] |
| 6 | 10 | 15 | 2541 тыс. рублей |
| 7 | -0.25 | 16 | 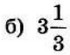 |
| 8 | 220 | 17 | 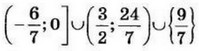 |
| 9 | 52 | 18 | а) 42; б) положительных; в) 24 |
| Вариант 21 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 113 | 10 | 15 |
| 2 | 60 | 11 | 7 |
| 3 | 0.2 | 12 | 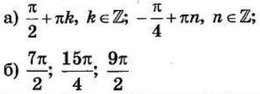 |
| 4 | 0.973 | 13 | 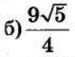 |
| 5 | 5.5 | 14 | 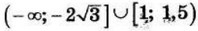 |
| 6 | 324 | 15 | 500 тыс. рублей |
| 7 | 2 | 16 | б) 4.8 |
| 8 | 6250 | 17 | 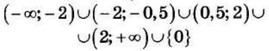 |
| 9 | 14 | 18 | 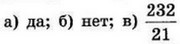 |
| Вариант 22 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | 3.4 |
| 2 | 45 | 11 | 1.2 |
| 3 | 0.3 | 12 | 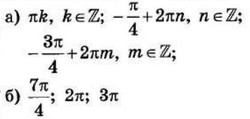 |
| 4 | 0.9744 | 13 |  |
| 5 | 11 | 14 | 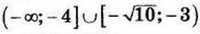 |
| 6 | -7.5 | 15 | 20 |
| 7 | 7 | 16 | б) 7.5 |
| 8 | 1.3 | 17 | [1; 9) |
| 9 | 5 | 18 | а) да; б) нет; в) 10 |
| Вариант 23 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 62 | 10 | 28 |
| 2 | 25 | 11 | 18 |
| 3 | 0.25 | 12 | 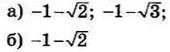 |
| 4 | 0.3 | 13 | 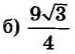 |
| 5 | -2 | 14 | (-∞; -1) ∪ {0} ∪ (0.5; +∞) |
| 6 | 80 | 15 | 35 700 рублей |
| 7 | 6 | 16 | 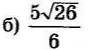 |
| 8 | 60 | 17 |  |
| 9 | 75 | 18 | а) 7; б) 15; в) 14 |
| Вариант 24 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 78 | 10 | -28 |
| 2 | 20 | 11 | -2 |
| 3 | 0.2 | 12 | 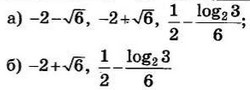 |
| 4 | 0.82 | 13 | 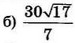 |
| 5 | 0 | 14 | 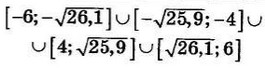 |
| 6 | 28 | 15 | 53 820 рублей |
| 7 | 6 | 16 | 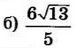 |
| 8 | 30 | 17 | 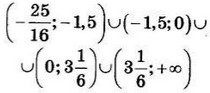 |
| 9 | 10 | 18 | а) 12; б) 15; в) 6 |
| Вариант 25 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 37 | 10 | -0.4 |
| 2 | 135 | 11 | 14 |
| 3 | 0.18 | 12 | 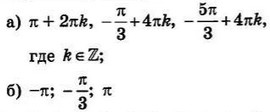 |
| 4 | 3 | 13 | б) 36 |
| 5 | 0.8 | 14 | 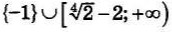 |
| 6 | 0.4 | 15 | 1 080 000 рублей |
| 7 | -0.2 | 16 | 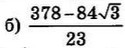 |
| 8 | 6 | 17 | 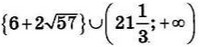 |
| 9 | 35 | 18 | а) нет; б) 21; в) 82 |
| Вариант 26 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 53 | 10 | -13 |
| 2 | 72 | 11 | 1 |
| 3 | 0.38 | 12 | 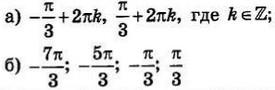 |
| 4 | 5 | 13 | б) 189 |
| 5 | -4 | 14 | (-0.5; 0.5) ∪ (0.5; 624.5) |
| 6 | -0.3 | 15 | 1 706 400 рублей |
| 7 | -0.75 | 16 | б) 91(5√2 — 7) |
| 8 | 96 | 17 | 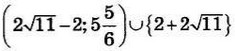 |
| 9 | 28 | 18 | а) нет; б) 36; в) 182 |
| Вариант 27 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 29 | 10 | 76 |
| 2 | 315 | 11 | -3 |
| 3 | 0.14 | 12 | 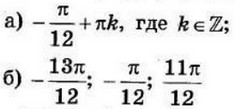 |
| 4 | 0.03 | 13 | б) 45° |
| 5 | 4 | 14 | (-1; 0) ∪ {log53} |
| 6 | 2.72 | 15 | 54 925 рублей |
| 7 | 6 | 16 | б) 8 |
| 8 | 7 | 17 | [0; 1.5) ∪ [2; +∞) |
| 9 | 77 | 18 | а) да; б) нет; в) 16 |
| Вариант 28 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | -5 |
| 2 | 176 | 11 | 38 |
| 3 | 0.375 | 12 | 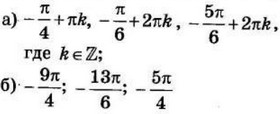 |
| 4 | 0.012 | 13 | 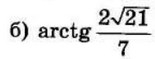 |
| 5 | -1 | 14 |  |
| 6 | -3 | 15 | 78 125 рублей |
| 7 | -3 | 16 | б) 18 |
| 8 | 28 | 17 | 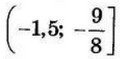 |
| 9 | 6 | 18 | а) да; б) нет; в) 12 |
| Вариант 29 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 60 | 10 | 67 |
| 2 | 18 | 11 | -21 |
| 3 | 0.24 | 12 | 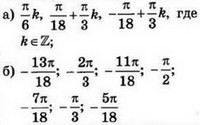 |
| 4 | 0.2 | 13 | б) 36 + 30√2 |
| 5 | 3 | 14 | [2; 5) |
| 6 | 4 | 15 | 126 694.4 рубля |
| 7 | 4 | 16 | б) 1 |
| 8 | 6.5 | 17 | 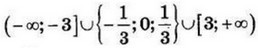 |
| 9 | 6.4 | 18 | а) да; б) нет; в) 2805 |
| Вариант 30 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 64 | 10 | 3 |
| 2 | 4 | 11 | -8 |
| 3 | 0.28 | 12 |  |
| 4 | 0.6 | 13 | 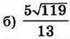 |
| 5 | 4 | 14 | (0; 5] |
| 6 | 8 | 15 | 1-й объект — 7 человек 2-й объект — 23 человека; 43 150 рублей |
| 7 | 14 | 16 | б) 50 |
| 8 | 9.6 | 17 | 4 < a ≤ 16 |
| 9 | 22 | 18 | а) да; б) нет; в) 2220 |
| Вариант 31 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6.5 | 10 | -7 |
| 2 | 54 | 11 | 8 |
| 3 | 0.98 | 12 | 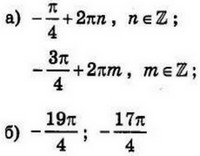 |
| 4 | 0.2 | 13 | 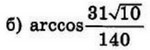 |
| 5 | 2 | 14 | [-2; 2) |
| 6 | -10 | 15 | 39 |
| 7 | 2 | 16 | б) 9√2 |
| 8 | 25 | 17 | 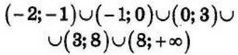 |
| 9 | 54 | 18 | а) нет; б) нет; в) 676 г. |
| Вариант 32 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 30 | 10 | 13 |
| 2 | 27 | 11 | -9 |
| 3 | 0.024 | 12 | 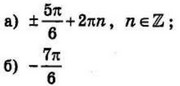 |
| 4 | 0.15 | 13 | 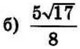 |
| 5 | -2 | 14 | (-2; 1) ∪ (1; 2) |
| 6 | 91 | 15 | 1.6 млн рублей |
| 7 | 3 | 16 | б) 27√3 |
| 8 | 17 | 17 | 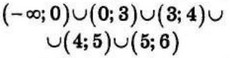 |
| 9 | 12 | 18 | а) нет; б) нет; в) 240 г |
| Вариант 33 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 72.5 | 10 | -2.5 |
| 2 | 47 | 11 | 26 |
| 3 | 0.28 | 12 | 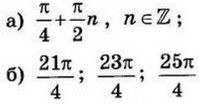 |
| 4 | 0.097 | 13 | б) 13√6 |
| 5 | -5 | 14 | 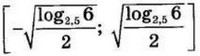 |
| 6 | 65 | 15 | 2.58 |
| 7 | 3 | 16 | б) 5 : 7 |
| 8 | 8 | 17 | 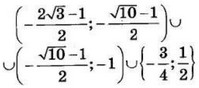 |
| 9 | 48 | 18 | а) нет; б) нет; в) 3 |
| Вариант 34 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 68 | 10 | -0.25 |
| 2 | 76 | 11 | -1 |
| 3 | 0.16 | 12 | 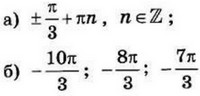 |
| 4 | 0.068 | 13 | б) 48.5 |
| 5 | 6 | 14 | 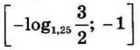 |
| 6 | 16 | 15 | 4.05 |
| 7 | 6 | 16 | б) 10 : 11 |
| 8 | 633 | 17 | 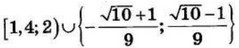 |
| 9 | 64 | 18 | а) да; б) нет; в) 5 |
| Вариант 35 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 21 | 10 | 0.75 |
| 2 | 200 | 11 | 9 |
| 3 | 0.56 | 12 | 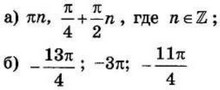 |
| 4 | 0.9 | 13 | б) 4√3 |
| 5 | -2 | 14 | [3 — √5; 2.8] ∪ [3.2; 3 + √5] |
| 6 | 7.5 | 15 | 20 |
| 7 | 0.5 | 16 | б) 1 : 3 : 1 |
| 8 | 0.31 | 17 | [-3; 22] |
| 9 | 20 | 18 | а) да; б) 180; в) 546 |
| Вариант 36 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | -0.5 |
| 2 | 88 | 11 | 30 |
| 3 | 0.12 | 12 | 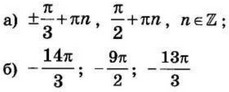 |
| 4 | 12 | 13 | б) 6√3 |
| 5 | -5 | 14 | 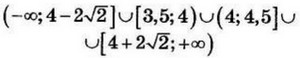 |
| 6 | 2.5 | 15 | 3 |
| 7 | 5.5 | 16 | б) 4 : 5 : 4 |
| 8 | 1.728 | 17 | (-∞; 4 — 2√2] ∪ ∪ [3.5; 4) ∪ ∪ (4; 4.5] ∪ ∪ [4 + 2√2; +∞) |
| 9 | 756 | 18 | а) да; б) 270; в) 17 |
Наверх

Скачать бесплатно сборник Ященко И.В. ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с ответами и решением.
Скачать сборник Ященко ЕГЭ 2023 в PDF
Аннотация к сборнику «ЕГЭ 2023. Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
Ященко ЕГЭ 2023 математика профиль 36 вариантов
В сборнике представлены: -36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2023 года; — инструкция по выполнению экзаменационной работы; — ответы ко всем заданиям; — решения и критерии оценивания заданий 12-18.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ. Под редакцией И. В. Ященко.
-
Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
-
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением