Задание 1
Найдите корень уравнения $$(x-11)^4=(x+3)^4.$$
Ответ: 4
Скрыть
$$(x-11)^4=(x+3)^4$$
$$((x-11)^2)^2=((x+3)^2)^2$$
Извлекаем квадратный корень от обеих частей уравнения:
$$(x-11)^2=(x+3)^2$$
$$x^2-22x+121=x^2+6x+9$$
$$x^2-22x-x^2-6x=9-121$$
$$-28x=-112$$
$$x=frac{-112}{-28}=4$$
Задание 2
В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Индии.
Ответ: 0.28
Скрыть
На первом месте может оказаться любой спортсмен из $$n=5+4+9+7=25$$ спортсменов, участвующих в соревнованиях. При этом число спортсменов из Индии равно $$m=7.$$ Следовательно, вероятность того, что спортсмен, который выступает первым, окажется из Индии, равна:
$$P=frac{m}{n}=frac{7}{25}=0,28$$
Задание 3
В треугольнике АВС средняя линия DE параллельна стороне АВ. Найдите площадь треугольника АВС, если площадь трапеции ABED равна 48.
Ответ: 64
Скрыть
Пусть вся площадь треугольника ABC равна $$x.$$ Тогда площадь малого треугольника CDE равна $$frac{x}{4}$$ (так как все его линейные размеры в 2 раза меньше соответствующих размеров треугольника ABC). Можно записать равенство:
$$x=frac{x}{4}+48$$
$$frac{3}{4}x=48$$
$$x=48cdotfrac{4}{3}=64$$
Задание 4
Найдите значение выражения $$frac{(sqrt{20}+sqrt{12})^2}{4+sqrt{15}}.$$
Ответ: 8
Скрыть
$$frac{(sqrt{20}+sqrt{12})^2}{4+sqrt{15}}=frac{(sqrt{20})^2+2sqrt{20}cdotsqrt{12}+(sqrt{12})^2}{4+sqrt{15}}=$$
$$=frac{20+2sqrt{240}+12}{4+sqrt{15}}=frac{32+2sqrt{16cdot15}}{4+sqrt{15}}=frac{32+8sqrt{15}}{4+sqrt{15}}=frac{8(4+sqrt{15}}{4+sqrt{15}}=8$$
Задание 5
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах.
Ответ: 4
Скрыть
Объем жидкости остается неизменным. Пусть изначально она равна
$$V=hcdotpi R^2$$
где h=25 см – высота; R – радиус основания первого сосуда. По условию задания диаметр второго сосуда в 2,5 больше первого, значит,
$$R_2=2,5cdotfrac{D}{2}=2,5R$$
Выразим тот же объем V через высоту $$h_2$$ и радиус $$R_2:$$
$$V=h_2cdotpi R^2_2=h_2cdotpicdot6,25R^2$$
Приравниваем эти величины и находим $$h_2:$$
$$h_2cdotpicdot6,25R^2=hcdotpi R^2$$
$$h_2=frac{h}{6,25}=frac{25}{6,25}=4$$
Задание 6
Материальная точка движется прямолинейно по закону $$x(t)=frac{1}{2}t^3-2t^2+6t+25,$$ где х — расстояние от точки отсчёта в метрах, t — время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени $$t=4.$$
Ответ: 14
Скрыть
Скорость — это производная от расстояния:
$$v(t)=x'(t)=frac{3}{2}t^2=4t+6$$
Находим скорость в момент времени $$t=4$$ с:
$$v(4)=frac{3}{2}cdot4^2-4cdot4+6=3cdot8-16+6=14$$
Задание 7
Водолазный колокол, содержащий $$v=2$$ моль воздуха при давлении $$р_1=2,4$$ атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления $$р_2$$ в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле $$A=alpha vTlog_2frac{p_2}{p_1},$$ где $$alpha=13,5 frac{Дж}{Мольcdot К}$$ — постоянная, $$Т=300$$ К — температура воздуха. Найдите, какое давление $$р_2$$ будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в $$16 200$$ Дж. Ответ дайте в атмосферах.
Ответ: 9,6
Скрыть
$$A=alpha vTlog_2frac{p_2}{p_1}$$
$$16200=13,5cdot2cdot300cdotlog_2frac{p_2}{2,4}$$
$$16200=8100cdotlog_2frac{p_2}{2,4}$$
$$log_2frac{p_2}{2,4}=frac{16200}{8100}$$
$$log_2frac{p_2}{2,4}=2$$
$$2^2=frac{p_2}{2,4}$$
$$4=frac{p_2}{2,4}$$
$$p_2=4cdot2,4=9,6$$
Задание 8
Первая труба заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая труба заполняет резервуар объёмом 396 литров. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба?
Ответ: 22
Скрыть
Пусть x литров воды в минуту пропускает вторая труба. Соответственно, первая труба будет пропускать $$x-2$$ литров воды в минуту. Резервуар объемом 396 литров вторая труба будет заполнять $$frac{396}{x}$$ минут, а резервуар объемом 440 литра первая труба заполняет $$frac{440}{x-2}$$ минут. Так как первая заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая, получаем уравнение:
$$frac{440}{x-2}-frac{396}{x}=4$$
откуда
$$440x-396cdot(x-2)=4cdot(x^2-2x)$$
$$110x-99x+198-x^2+2x=0$$
$$x^2-13-198=0$$
$$D=169+792=961=31^2$$
$$x_1=frac{13+31}{2}=22$$
$$x_2=frac{13-31}{2}<0$$
Получаем пропускную способность второй трубы 22 литра в минуту.
Задание 9
На рисунке изображены графики функций $$f(x)=-2x^2-2x+4$$ и $$g(x)=ax^2+bx+с,$$ которые пересекаются в точках $$A(-1; 4)$$ и $$B(x_0; y_0).$$ Найдите $$x_0.$$
Ответ: 3
Скрыть
Абсцисса вершины для $$f(x): x_0=-frac{(-2)}{(-2)cdot2}=-frac{1}{2}$$
Это правая парабола.
$$g(x)cap Oy$$ в точке $$(0;1),$$ значит $$c=1.$$
Точки $$A(-2;5)$$ и $$C(-4;1)$$ принадлежат $$g(x).$$ Тогда:
$$left{begin{matrix} 5=acdot(-2)^2+bcdot(-2)+1\ 1=acdot(-4)^2+bcdot(-4)+1 end{matrix}right.Leftrightarrowleft{begin{matrix} 4=4a-2b\ 0=16a-4b end{matrix}right.Leftrightarrowleft{begin{matrix} 2=2a-b\ 4a=b end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} 2=2a-4a\ b=4a end{matrix}right.Leftrightarrowleft{begin{matrix} a=-1\ b=-4 end{matrix}right.$$
Получили $$g(x)=-x^2-4x+1$$
Тогда:
$$-2x^2-2x+4=-x^2-4x+1$$
$$x^2-2x-3=0$$
$$left[begin{matrix} x_1=3\ x_2=-1 end{matrix}right.$$
Задание 10
За круглый стол на 6 стульев в случайном порядке рассаживаются 4 мальчика и 2 девочки. Найдите вероятность того, что обе девочки не будут сидеть рядом.
Ответ: 0,6
Скрыть
Посадим первую девочку за стол. Таким образом у нас останется 1 девочка и 5 стульев. Сесть она может только на два стула — по обе стороны от уже сидящей девочки. Отсюда вероятность того, что девочки сядут рядом: $$frac{2}{5}=0,4$$ следовательно вероятность того, что они не будут сидеть рядом равна $$1-0,4=0,6$$
Задание 11
Найдите точку минимума функции $$y=(x+8)^2cdot е^{-x-3}.$$
Ответ: -8
Скрыть
$$y=(x+8)^2cdot е^{-x-3}$$
Найдём производную функции:
$$y’=((x+8)^2)’cdot е^{-x-3}+(x+8)^2cdot(e^{-x-3})’=2(x+8)cdot e^{-x-3}+(x+8)^2cdot(-e^{-x-3})=$$
$$=e^{-x-3}cdot(2(x+8)-(x+8)^2)=e^{-x-3}cdot(-x^2-14x-48)$$
Найдём нули производной:
$$e^{-x-3}cdot(-x^2-14x-48)=0$$
$$e^{-x-3}>0$$ всегда
$$-x^2-14x-48=0$$
$$x^2+14+48=0$$
Через дискриминант находим корни уравнения:
$$x_1=-8$$
$$x_2=-6$$
Определим знаки производной функции и изобразим поведение функции:
Точка минимума: $$x=-8.$$
Задание 12
а) Решите уравнение $$cos 2xsin 2xsinfrac{2pi }{3}=frac{1}{4}{rm cos}(8x-frac{3pi }{2})$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[frac{8pi }{3}; frac{10pi }{3}]$$
Ответ: а) $$frac{pi}{4} k, frac{5pi}{24}+frac{pi}{2}k, -frac{5pi}{24}+frac{pi}{2}k, kin Z$$; б) $$frac{65pi}{24}; frac{11pi}{4}; frac{67pi}{24}; 3pi ; frac{77pi}{24}; frac{13pi}{4}; frac{79pi}{24}$$
Скрыть
а)
$$cos 2xsin 2xsinfrac{2pi}{3}=frac{1}{4}cos(8x-frac{3pi}{2}$$
$$frac{1}{2}cdot(2sin 2xcos 2x)sin(pi-frac{pi}{3})=frac{1}{4}cos(frac{3pi}{2}-8x)$$
$$frac{1}{2}sin 4xsinfrac{pi}{3}=frac{1}{4}cdot(-sin 8x)$$
$$frac{1}{2}sin 4xcdotfrac{sqrt{3}}{2}=-frac{1}{4}sin(2cdot 4x)$$
$$sqrt{3}sin 4x+2sin 4xcos 4x=0$$
$$sin 4x(sqrt{3}+2cos 4x)=0$$
$$sin 4x=0$$
$$4x=pi k, kin Z$$
$$x=frac{pi k}{4}, kin Z$$
$$sqrt{3}+2cos 4x=0$$
$$cos 4x=-frac{sqrt{3}}{2}$$
$$4x=pmarccos(-frac{sqrt{3}}{2})+2pi n, nin Z$$
$$4x=pm(pi-arccosfrac{sqrt{3}}{2})+2pi n, nin Z$$
$$4x=pm(pi-frac{pi}{6})+2pi n, nin Z$$
$$4x=pmfrac{5}{6}+2pi n, nin Z$$
$$x=pmfrac{5}{24}+frac{pi n}{2}, nin Z$$
б)
С помощью двойного неравенства отберём корни на отрезке $$[frac{8pi}{3};frac{10pi}{3}]$$
1) $$frac{8pi}{3}leqfrac{pi k}{4}leqfrac{10pi}{3}Leftrightarrowfrac{32}{3}leq kleqfrac{40}{3}, kin ZRightarrow k=11;12;13$$
$$k=11: x=frac{picdot11}{4}=frac{11pi}{4}$$
$$k=12: x=frac{picdot12}{4}=3pi$$
$$k=13: x=frac{picdot13}{4}=frac{13pi}{4}$$
2) $$frac{8pi}{3}leqfrac{5pi}{24}+frac{pi k}{2}leqfrac{10pi}{3}Leftrightarrowfrac{64-5pi}{24}cdotfrac{2}{pi}leq kleqfrac{80pi-5pi}{24}cdotfrac{2}{pi}Leftrightarrow$$
$$Leftrightarrowfrac{59}{12}leq kleqfrac{75}{12}, kin ZRightarrow k=5;6$$
$$k=5: x=frac{5pi}{24}+frac{picdot5}{2}=frac{65pi}{24}$$
$$k=6: x=frac{5pi}{24}+frac{picdot6}{2}=frac{77pi}{24}$$
3) $$frac{8pi}{3}leq-frac{5pi}{24}+frac{pi k}{2}leqfrac{10pi}{3}Leftrightarrowfrac{64+5}{12}leq kleqfrac{80+5}{12}, kin ZRightarrow k=6;7$$
$$k=6: x=-frac{5pi}{24}+frac{picdot6}{2}=frac{67pi}{24}$$
$$k=7: x=-frac{5pi}{24}+frac{picdot7}{2}=frac{79pi}{24}$$
Задание 13
Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Ответ: $$frac{5sqrt{119}}{13}$$
Скрыть
а) Известно, что образующие конуса равны, то есть, AB = BC. По условию сечение проходит через AB, BC и вершину B, следовательно, сечение – это равнобедренный прямоугольный треугольник ABC.
б) Расстояние от центра основания O до плоскости сечения – это перпендикуляр OP, который также можно воспринимать как высоту прямоугольного треугольника BON с площадью:
$$S_{BON}=frac{1}{2}OPcdot NB=frac{1}{2}ONcdot OB$$
Отсюда, имеем:
$$OP=frac{ONcdot OB}{NB}$$
Найдем сначала длины образующих AB и BC, зная, что радиус основания 12, а высота конуса OB = 5:
$$AB=BC=sqrt{12^2+5^2}=13$$
Затем, из прямоугольного треугольника AB. Cнайдем AC:
$$AC=sqrt{13^2+13^2}=13sqrt{2}$$
Следовательно,
$$NC=frac{1}{2}AC=frac{13sqrt{2}}{2}$$ и $$BN=sqrt{BC^2-NC^2}=sqrt{13^2-frac{13^2}{2}}=frac{13sqrt{2}}{2}$$
Далее, из прямоугольного треугольника ONC находим ON:
$$ON=sqrt{OC^2-NC^2}=sqrt{144-frac{169}{2}}=sqrt{frac{119}{2}}$$
Получаем значение расстояния OP:
$$OP=frac{sqrt{frac{119}{2}}cdot5}{frac{13sqrt{2}}{2}}=frac{5sqrt{119}}{13}$$
Задание 14
Решите неравенство $$30cdot3^{log_2(7-x)}+3^{1+log_2 x}-3^{log_2(7x-x^2)}geq90.$$
Ответ: $$(0;5]$$
Скрыть
ОДЗ: $$left{begin{matrix} 7-x>0\ x>0\ x(7-x)>0 end{matrix}right.left{begin{matrix} xin (0;7)\ xin (0;7) end{matrix}right.Rightarrow xin (0;7)$$
$$30cdot3^{log_2(7-x)}+3cdot3^{log_2 x}-3^{log_2 x}-3^{log_2(7-x)}-90geq0$$
$$30cdot(3^{log_2(7-x)}-3)+3^{log_2 x}(3-3^{log_2(7-x)}-90geq0$$
$$(3^{log_2(7-x)}-3)cdot(30-3^{log_2 x})geq0$$
$$f(x)=log_2 x$$ на промежутке $$(0;7)$$ возрастает. Наибольшее значение меньше $$log_2 7<3=log_2 8. 3^{log_2 7}<27$$
$$Rightarrow$$ на $$ОДЗ xin (0;7)$$ разность $$30-3^{log_2 x}>0.$$
Осталось решить неравенство $$3^{log_2(7-x)}-3geq0$$
$$left{begin{matrix} xin (0;7)\ log_2(7-x)geq1 end{matrix}right.left{begin{matrix} xin (0;7)\ xleq5 end{matrix}right.$$
$$xin (0;5]$$
Задание 15
Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает $$р$$ человек, то каждый из них получает в сутки $$200р$$ рублей. Если на втором объекте работает $$р$$ человек, то каждый из них получает в сутки $$(50р+300)$$ рублей. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?
Ответ: 1-й объект — 7 человек, 2-й объект — 23 человека; 43 150 рублей
Скрыть
Пусть на втором объекте работает $$k$$ рабочих, тогда на 1-м будет работать $$30-k$$ рабочих. Получаем суммарное значение их зарплаты:
$$f(k)=(30-k)cdot200cdot(30-k)+kcdot(50k+300)$$
$$f(k)=(30-k)^2cdot200+50k^2+300k$$
Найдем такое $$k,$$ при котором функция принимает наименьшее значение, то есть, вычислим точку экстремума:
$$f'(k)=-400cdot(30-k)+100k+300=0$$
$$500k=11700$$
$$k=frac{11700}{500}=23,4$$
Так как число рабочих – целое число, то $$k=23.$$ Получаем, что на первом объекте работает $$30-23=7$$ рабочих, а на втором – $$23.$$ Их суммарная зарплата, составит:
$$7^2cdot200+23cdot(50cdot23+300)=43150$$ рублей
Задание 16
На сторонах АС, АВ и ВС прямоугольного треугольника АВС с прямым углом С во внешнюю сторону построены равнобедренные прямоугольные треугольники АКС, ALB и ВМС с прямыми углами К, L и М соответственно.
а) Докажите, что LC — высота треугольника KLM.
б) Найдите площадь треугольника KLM, если$$ LC =10.$$
Ответ: 50
Скрыть
а) Рассмотрим четырехугольник ALBC, у которого углы $$ACB=ALB=90^{circ},$$ а значит, вокруг него можно описать окружность (по свойству: сумма противоположных углов $$ACB+ALB=180^{circ}$$). Тогда хорды AL = LB (треугольники АКС, ALB и ВМС – равнобедренные) стягивают дуги $$cup AL=cup LB,$$ следовательно, вписанные углы, опирающиеся на эти дуги, также равны: $$angle ACL=angle LCB=45^{circ};$$ $$angle KCA+angle ACL=45^{circ}+45^{circ}=90^{circ};$$ $$angle LCB+angle BCM=90^{circ},$$ следовательно, LC перпендикулярна KM и LC – высота треугольника KLM.
б) Площадь треугольника KLM можно найти по формуле:
$$S_{KLM}=frac{1}{2}KMcdot LC$$
Пусть BC = a, AC = b, CL = d, AB = c, а P – точка пересечения AB и CL. Так как $$angle ACP=angle BCP=45^{circ},$$ то CB – биссектриса треугольника ABC. По свойству биссектрис:
$$frac{AP}{PB}=frac{AC}{CB}=frac{b}{a}$$
Учитывая, что AP + PB = AB = c, получаем систему:
$$frac{AP}{PB}=frac{b}{a}$$
$$AP+PB=c$$
С решением:
$$AP=frac{bc}{a+b}; PB=frac{ac}{a+b}$$
Так как углы $$angle ACL=angle BAL=45^{circ},$$ то треугольники ACL и PAL подобны по двум углам и:
$$frac{AC}{PA}=frac{CL}{AL}Rightarrow b: frac{bc}{a+b}=d:frac{c}{sqrt{2}}$$
и $$d=frac{a+b}{sqrt{2}}.$$ Из равенства KM = KC + CM, получаем:
$$KM=frac{a}{sqrt{2}}+frac{b}{sqrt{2}}=d=10$$
Следовательно:
$$S_{KLM}=frac{1}{2}10cdot10=50$$
Задание 17
Найдите все значения а, при каждом из которых система уравнений
$$left{begin{matrix} log_{11}(a-y^2)=log_{11}(a-x^2),\ x^2+y^2=2x+6y end{matrix}right.$$
имеет ровно два различных решения.
Ответ: $$4<aleq16$$
Скрыть
$$left{begin{matrix} log_{11}(a-y^2)=log_{11}(a-x^2),\ x^2+y^2=2x+6y end{matrix}right.$$
Решение системы определяем при
$$left{begin{matrix} a-x^2>0\ a-y^2>0 end{matrix}right.Leftrightarrowleft{begin{matrix} a>x^{2} (*)\ a>y^2 end{matrix}right.$$
На $$(*)$$ получили:
$$left{begin{matrix} -y^2=-x^2\ x^2+y^2-2x-6y=0 end{matrix}right.$$
$$1) left{begin{matrix} y=x\ x^2+x^2-2x-6x=0 end{matrix}right.Leftrightarrowleft{begin{matrix} y=x\ 2x^2-8x=0 end{matrix}right.Leftrightarrowleft{begin{matrix} y=x\ left[begin{matrix} x=0\ x=4 end{matrix}right. end{matrix}right.Leftrightarrow (0;0); (4;4)$$
С учётом $$(*):left{begin{matrix} a>0^2\ a>4^2 end{matrix}right.Rightarrow a>16$$
$$2) left{begin{matrix} y=-x\ x^2+x^2-2x+6x=0 end{matrix}right.Leftrightarrowleft{begin{matrix} y=-x\ 2x^2+4x=0 end{matrix}right.Leftrightarrowleft{begin{matrix} y=-x\ left[begin{matrix} x=0\ x=-2 end{matrix}right. end{matrix}right.Leftrightarrow (0;0); (-2;2)$$
С учётом $$(*):left{begin{matrix} a>(-2)^2\ a>2^2 end{matrix}right.Rightarrow a>4$$
Получили: при $$a>0$$ есть решение, при $$a>4$$ добавляется ещё одно, при $$a>16$$ ещё одно.
Тогда ровно 2 решения при $$ain (4;16]$$
Задание 18
Для набора 40 различных натуральных чисел выполнено, что сумма любых двух чисел из этого набора меньше суммы любых четырёх чисел из этого набора.
а) Может ли одним из этих чисел быть число 777?
б) Может ли одним из этих чисел быть число 33?
в) Какое наименьшее значение может принимать сумма чисел этого набора?
Ответ: а) да; б) нет; в) 2220
Скрыть
Упорядочим числа по возрастанию x1 < x2 < … < x40. Заметим сразу, что достаточно проверять условие только для двух самых больших и четырех самых маленьких чисел.
а), б) В наборе 33, 777, 778, …, 815 выполнено
$$815 + 814 < 33 + 777 + 778 + 779.$$
в) Будем говорить, что с набором чисел можно сделать какую-то операцию, если после ее выполнения условие
$$x_1+x_2+x_3+x_4>x_28+x_29+x_30$$
не может нарушиться, числа останутся разными, а сумма чисел во всем наборе не становится больше. Если x40 ≠ x39 + 1, то можно заменить x40 на x39 + 1. Если после этого x39 ≠ x38 + 1, то можно заменить x39 на x38 + 1 и x40 на x38 + 2. Продолжая эти действия (сдвиг больших чисел вниз), мы в итоге получим набор чисел, идущих подряд, кроме может быть первого (даже все числа от x3 до x40 можно синхронно уменьшать, поскольку обе части неравенства
$$x_1+x_2+x_3+x_4>x_39+x_40$$
будут уменьшаться одинаково). Далее можно увеличивать на 1 первое число и уменьшать на 1 все остальные. Так можно делать, если x2 − x1 > 2.
Итак, оптимальный набор — это числа x, x + 1, x + 2, …, x + 39 или x − 1, x + 1, x + 2, …, x + 39, причем в первом случае 4x + 6 > 2x + 77, откуда x ≥ 36, а во втором 4x + 5 > 2x + 77, откуда x ≥ 37. В наборе 36, 37, …, 75 сумма очевидно меньше, чем в наборе 36, 38, 39, …, 76. Значит, минимальная сумма равна
$$(xcdot36+39)cdot20=2220,$$
а примером могут служить числа от 36 до 75.
| 3256 | В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Индии |
В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 5 из Японии, 4 из Кореи, 9 из Китая и 7 из Индии ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 2 | |
| 3255 | Найдите значение выражения (sqrt(20)+sqrt(12))^2/(4+sqrt(15)) |
Найдите значение выражения (sqrt 20 + sqrt 12)2 / 4+sqrt15 ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 4 | |
| 3254 | В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах |
В цилиндрическом сосуде уровень жидкости достигает 25 см ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 5 | |
| 3253 | Материальная точка движется прямолинейно по закону x(t)=1/2t^3-2t^2+6t+25, где x — расстояние от точки отсчёта в метрах, t — время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=4 |
Материальная точка движется прямолинейно по закону x(t)= 1/2t3 -2t2 +6t +25 ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 6 | |
| 3252 | На рисунке изображены графики функций f(x)=-2x^2-2x+4 и g(x)=ax^2+bx+c., которые пересекаются в точках A(-1; 4) и B(x0; y0). Найдите x0
|
На рисунке изображены графики функций f(x)=-2×2 — 2x + 4 и g(x)=ax2 + bx +c ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 9 | |
| 2606 | Первая труба заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая труба заполняет резервуар объёмом 396 литров. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба? |
Первая труба заполняет резервуар ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 20 Задание 8 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 11 | |
| 2605 | а) Решите уравнение cos(2x)*sin(2x)*sin((2pi)/3)=1/4*cos(8x-(3pi)/2) б) Укажите корни этого уравнения, принадлежащие отрезку [(8pi)/3; (10pi)/3]. |
Решите уравнение cos(2x) sin(2x) sin((2pi)/3) =1/4 cos(8x- (3pi)/2) ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 20 Задание 12 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 13 | |
| 2604 | Решите неравенство 30*3^(log_{2}(7-x))+3^(1+log_{2}(x))-3^(log_{2}(7x-x^2)) >= 90 |
Решите неравенство 30*3^(log_{2}(7- x)) + 3^(1+ log_{2}(x))- 3^(log_{2}(7x -x^2)) >= 90 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 20 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 15 | |
| 2603 | Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса |
Радиус основания конуса равен 12, а высота конуса равна 5 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 20 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 14 | |
Напиши мне, решений каких вариантов не хватает на сайте?
Например: «Сборник Лысенко ЕГЭ 2023 профиль 40 вариантов», «Варианты Ларина ЕГЭ 2023 профиль», «Варианты СтатГрад ЕГЭ 2023 профиль» и т.п.
Варианты СтатГрад ЕГЭ 2023 (профильный уровень)
Варианты сборника И.В. Ященко ЕГЭ 2023 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2022 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2021 (профильный уровень), 36 вариантов.
Варианты сборника Ф.Ф. Лысенко ЕГЭ 2021 (профильный уровень), 40 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2020 (профильный уровень), 36 вариантов.
Задачу №1 правильно решили 24 840 человек, что составляет 72% от выпускников города. Сколько всего выпускников в этом городе?
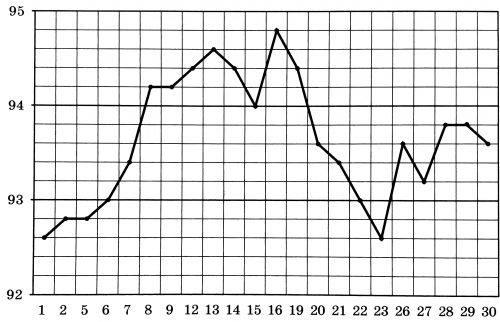
На рисунке показан курс индийской рупии, установленный Центробанком на все рабочие дни марта 2019 года. По горизонтали указаны числа месяца, по вертикали — цена 100 индийских рупий в рублях. Для наглядности точки соединены отрезками.
Определите, сколько рабочих дней в период с 16 по 30 марта 2019 года стоимость 100 индийских рупий была ниже 94 рублей.
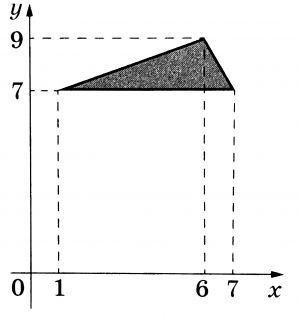
Найдите площадь треугольника, изображённого на рисунке.
В коробке 8 чёрных и 5 белых шаров. Случайным образом достают 6 шаров. Во сколько раз событие «среди выбранных шаров ровно четыре чёрных» более вероятно, чем событие «среди выбранных шаров ровно пять чёрных»?
Найдите корень уравнения (log_{7}{(x+18)}=2log_{7}{(2-x)}).Если уравнение имеет более одного корня, в ответе запишите наибольший из корней.
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 9. Найдите среднюю линию этой трапеции.
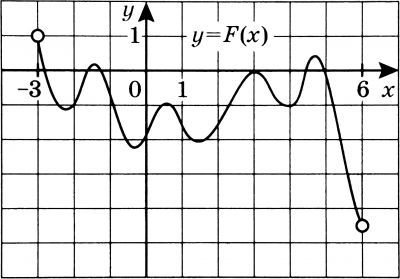
На рисунке изображён график функции (y=F(x)) одной из первообразных функции (f(x)), определённой на интервале (-3;6). Найдите количество решений уравнения (f(x)=0) на отрезке [-2; 5].
Шар вписан в цилиндр. Площадь поверхности шара равна 74. Найдите площадь полной поверхности цилиндра.
Найдите значение выражения (2{,}5^{frac{1}{7}}cdot2^{frac{2}{7}}cdot10^{frac{6}{7}})
Два тела, массой (m=10) кг каждое, движутся с одинаковой скоростью (v=10) м/с под углом (2alpha)друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле (Q=mv^2sin^2{alpha}), где (m)-масса в килограммах, (v)-скорость в м/с. Найдите, под каким наименьшим углом (2alpha)(в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 750 джоулей.
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 6 рабочих, во второй 15 рабочих. Через 5 дней после начала работы в первую бригаду перешли 7 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Найдите наименьшее значение функции (y=4x^2-12x+4ln{x}-10) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right])
а) Решите уравнение (125^{sin^2{x}}=(sqrt{5})^{5sin{2x}}cdot0{,}2)
б) Найдите все корни этого уравнения, принадлежащие промежутку ([-3pi;-2pi])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. (pi n,; ninmathbb{Z}) | 2. (dfrac{pi}{6}+pi n,; ninmathbb{Z}) | 3. (dfrac{pi}{4}+pi n,; ninmathbb{Z}) | 4. (dfrac{pi}{3}+pi n,; ninmathbb{Z}) |
| 5. (dfrac{pi}{2}+pi n,; ninmathbb{Z}) | 6. (dfrac{2pi}{3}+pi n,; ninmathbb{Z}) | 7. (dfrac{3pi}{4}+pi n,; ninmathbb{Z}) | 8. (dfrac{5pi}{6}+pi n,; ninmathbb{Z}) |
| 9. (mathrm{arctg,}dfrac15+pi n,; ninmathbb{Z}) | 10. (mathrm{arctg,}dfrac14+pi n,; ninmathbb{Z}) | 11. (mathrm{arctg,}dfrac13+pi n,; ninmathbb{Z}) | 12. (mathrm{arctg,}dfrac12+pi n,; ninmathbb{Z}) |
| 13. (-mathrm{arctg,}dfrac15+pi n,; ninmathbb{Z}) | 14. (-mathrm{arctg,}dfrac14+pi n,; ninmathbb{Z}) | 15. (-mathrm{arctg,}dfrac13+pi n,; ninmathbb{Z}) | 16. (-mathrm{arctg,}dfrac12+pi n,; ninmathbb{Z}) |
б)
| 17. (-3pi) | 18. (-dfrac{17pi}{6}) | 19. (-dfrac{11pi}{4}) | 20. (-dfrac{8pi}{3}) |
| 21. (-dfrac{6pi}{2}) | 22. (-dfrac{7pi}{3}) | 23. (-dfrac{9pi}{4}) | 24. (-dfrac{13pi}{6}) |
| 25. (-2pi) | 26. (mathrm{arctg,}dfrac15-3pi) | 27. (mathrm{arctg,}dfrac14-3pi) | 28.(mathrm{arctg,}dfrac13-3pi) |
| 29.(mathrm{arctg,}dfrac12-3pi) | 30. (-mathrm{arctg,}dfrac15-2pi) | 31. (-mathrm{arctg,}dfrac14-2pi) | 32. (-mathrm{arctg,}dfrac13-2pi) |
| 33. (-mathrm{arctg,}dfrac12-2pi) |
Основание пирамиды SABC — равносторонний треугольник ABC. Боковое ребро SA перпендикулярно плоскости основания, точки М и N — середины рёбер BC и AB соответственно, причём SN=AM.
а) Докажите, что угол между прямыми AM и SN равен 60°.
б) Найдите расстояние между этими прямыми, если BC=6.
Решите неравенство (log_{frac{1}{4}}{(5-5x)}leqslantlog_{frac{1}{4}}{(x^2-3x+2)}+log_{4}{(x+4)})
В треугольнике АВС все стороны различны. Прямая, содержащая высоту ВН треугольника АВС, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN-диаметр этой окружности.
а) Докажите, что AC и KN параллельны.
б) Найдите расстояние от точки N до прямой AC, если радиус описанной около треугольника ABC окружности равен 6√6, ∠BAC=30°, ∠ABC=105°
По бизнес-плану четырёхлетний проект предполагает начальное вложение — 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 12 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года вырастут как минимум в полтора раза, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Запишите значения n и m через точку с запятой без пробелов.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases}y=(a+2)x^2+2ax+a-2\y^2=x^2end{cases})имеет ровно четыре различных решения.
Сторона квадрата на 2 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
а) Может ли ширина прямоугольника быть равной 6?
б) Может ли длина прямоугольника быть равной 9?
в) Найдите все возможные варианты таких пар прямоугольников и квадратов.
Введите ответ в форме строки «да;да;1;2;3;4». Где ответы на пункты разделены «;», первые два ответа с маленькой буквы, а в пункте В перечислите возможные длины стороны квадрата по возрастанию через точку с запятой.
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36
Оригинальная фотография обложки новой книги в распечатанном виде
Язык Русский
Издатель Национальное образование
Год выхода 2021
Единый Государственный Экзамен на 2021 — 2022 учебный год. Официальный сайт. Открытый банк заданий. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. ФИОКО. Школа России. 21 век. ГДЗ и Решебник. Перспектива. Школа 2100. Планета знаний. Россия.
В новом учебном году 2022 года желаем вам сдать на отлично все экзамены и поступить в ВУЗ! Для успешной подготовки к ЕГЭ-22 предлагаем вам ознакомиться с содержимым нового учебника. Здесь вы сможете бесплатно скачать официальный учебник по ЕГЭ в формате PDF или ВОРД для подготовки к экзамену и самостоятельно решать из него задания. Также здесь можно скачать ответы, решения, пояснения и объяснения к заданиям учебника. Домашняя работа. Вариант 1, 2.
Новый рекомендуемый учебник в 2022 году для подготовки к экзаменам ЕГЭ — это новый сборник ЕГЭ-2022. Математика Базовый и профильный уровни Ященко И.В. типовые экзаменационные варианты: 20 вариантов
Данный учебник для основного экзамена в средней школе входит в Федеральный перечень учебников на 2021 — 2022 учебный год
На этой странице можно купить или бесплатно скачать электронную версию книги с ответами в формате ПДФ или ВОРД. В свободное время можно решать задачи из этого учебника онлайн и офлайн. А также проверить сразу решения и правильные ответы на задачи. Сборник заданий соответствует и удовлетворяет всем нормам школы России, ФИПИ и ФГОС. После подготовки к ЕГЭ2022 вы сможете смело сказать себе, что я решу ЕГЭ на 100 баллов! Учебник был взят с официального сайта.
В новом сборнике для подготовки к ЕГЭ-2022 представлены:
Пособие прошло научно-методическую оценку ФГБНУ «ФИПИ» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
В сборнике представлены:
— 10 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике базового уровня 2022 года;
— 10 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2022 года; — инструкции по выполнению экзаменационных работ;
— ответы ко всем заданиям; — решения и критерии оценивания.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации в форме ЕГЭ, а также объективно оценить уровень своей подготовки к экзамену. Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Наличие: Есть в наличии на складе
Заказать этот учебник за наличный или безналичный расчет с доставкой можно в Интернет-магазине или просто нажать кнопку КУПИТЬ
Цена книги уточняется (Вам позвонит менеджер и сообщит стоимость книги после заказа)
.