Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
В этой статье разберём задания 22-27.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Задание 22
В файле содержится информация о совокупности N вычислительных
процессов, которые могут выполняться параллельно или последовательно.
Будем говорить, что процесс B зависит от процесса A, если для выполнения
процесса B необходимы результаты выполнения процесса A. В этом случае
процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой
строке таблицы указан идентификатор процесса (ID), во второй строке
таблицы – время его выполнения в миллисекундах, в третьей строке
перечислены с разделителем «;» ID процессов, от которых зависит данный
процесс. Если процесс является независимым, то в таблице указано
значение 0.
Определите минимальное время, через которое завершится выполнение
всей совокупности процессов, при условии, что все независимые друг от
друга процессы могут выполняться параллельно.
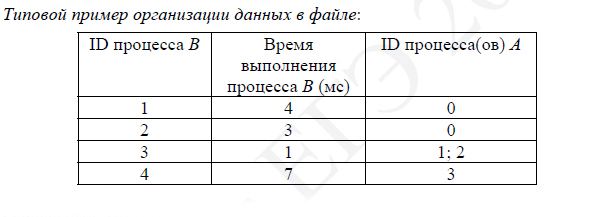
Типовой пример имеет иллюстративный характер. Для выполнения
задания используйте данные из прилагаемого файла.
Решение:
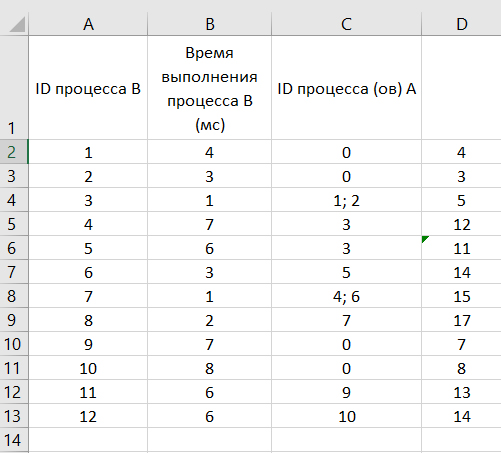
Здесь есть процессы, которые зависят от других процесов. В столбце D вычислим время для всех процесов, с учётом зависимости.
Если процесс зависит от двух процессов, то время ожидания будет равно самому медленному из этих процессов.
В столбце D пишем для каждой строчки: время процесса + время ожидания самого медленного процесса, от которого зависит этот процесс (если такие есть).
Получается такая картина:
Система заврешить работу, когда завершится самый медленный процесс.
Ответ: 17
Задание 23
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1
результатом является число 35, при этом траектория вычислений содержит
число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы 121 при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решение:
Будем решать с помощью шаблона на языке Python, который был представлен в видеокурсе по подготовке к ЕГЭ по информатике.
def F(x, y): if x == y: return 1 if x > y or x==17: return 0 if x < y: return F(x+1, y) + F(x*2, y) print(F(1, 10)*F(10, 35))
Ответ: 98
Задание 24
Текстовый файл состоит из символов A, B, C, D и O.
Определите максимальное количество идущих подряд пар символов вида
согласная + гласная
в прилагаемом файле.
Для выполнения этого задания следует написать программу.
Решение:
Подобная задача была рассмотрена в видеокурсе к ЕГЭ по информатике.
f=open('24_10.txt') s=f.read() s=s.replace('BA', '1') s=s.replace('CA', '1') s=s.replace('DA', '1') s=s.replace('BO', '1') s=s.replace('CO', '1') s=s.replace('DO', '1') k=0 kmax=0 for i in range(0, len(s)): if s[i]=='1': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
Ответ получается 24, но в официальном ответе 95. Дело в том, что в файле присутствует буква F, хотя в условии сказано, что файл состоит только из букв A, B, C, D и O. Следовательно, файл к задаче не верный.
Ответ: 24
Задание 25
Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:
– символ «?» означает ровно одну произвольную цифру;
символ «*» означает любую последовательность цифр произвольной
длины; в том числе «*» может задавать и пустую последовательность.
Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 1010, найдите все числа,
соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа
в порядке возрастания, а во втором столбце – соответствующие им
результаты деления этих чисел на 2023.
Количество строк в таблице для ответа избыточно.
Решение:
Подобная задача так же обсуждалась в видеокурсе и на обзоре реального экзамена ЕГЭ по информатике от 20.06.22
Если не учитывать звёздочку, число 1?21394 имеет семь разрядов. Максимальная верхняя граница 1010. Значит, для звёздочки есть три разряда.
#Вместо звёздочки ноль разрядов for x in '0123456789': s = '1' + x + '21394' i=int(s) if i%2023==0: print(i, i//2023) #Вместо звёздочки один разряд for x in '0123456789': for y in '0123456789': s = '1' + x + '2139' + y + '4' i=int(s) if i%2023==0: print(i, i//2023) #Вместо звёздочки два разряда for x in '0123456789': for y in '0123456789': for z in '0123456789': s = '1' + x + '2139' + y + z + '4' i=int(s) if i%2023==0: print(i, i//2023) #Вместо звёздочки три разряда for x in '0123456789': for y in '0123456789': for z in '0123456789': for w in '0123456789': s = '1' + x + '2139' + y + z + w + '4' i=int(s) if i%2023==0: print(i, i//2023)
Ответ:
| 162139404 | 80148 |
| 1321399324 | 653188 |
| 1421396214 | 702618 |
| 1521393104 | 752048 |
Задание 26
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробоку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Выходные данные
В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающая 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле.
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих упаковки «матрёшки», составлят 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
f=open('26.txt') n=int(f.readline()) a=[] for i in range(n): x=int(f.readline()) a.append(x) a.sort(reverse=True) k=1 p=a[0] for i in range(1, len(a)): if p-a[i]>=3: k=k+1 p=a[i] print(k, p)
В начале считываем все числа в массив (список) a. Сортируем их в порядке убывания.
Приступаем собирать упаковку. Начинаем с самой большой упаковки. Большую упаковку точно можно взять в наш подарок. Переменная p — это размер последний коробки, которую мы взяли. Переменная k — количество коробок в подарке на текущий момент времени.
Если следующая коробка подходит по условию, то мы её берём в наш подарок. Кто-то может подумать, что может выгоднее взять не самую большую коробку, а предпоследнего размера. Но все размеры которые будут подходить для предпоследнего элемента, точно будут подходить и для последнего, и количество упаковок точно не будет меньше, если мы берём самую большую коробку.
Дубликаты не влияют на ответы.
Если мы начинаем с самой большой коробки, то в самом конце в переменной p окажется максимальный размер самой маленькой коробки.
Ответ:
Задание 27
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла (файл А и файл B), каждый из которых в первой строке содержит число N ( 1 ≤ N ≤ 10 000 000) — количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла A, затем — для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1*2 + 3*1 + 5*1 + 6*1 + 8*2.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных варантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение:
import math f=open('27B.txt') k=9999995 n=int(f.readline()) a=[0]*k sm=0 for i in range(n): x, y = f.readline().split() x=int(x) y=int(y) z = math.ceil(y/36) a[x] = z sm = sm + (x-1)*z # Вспомогательные суммы s1=[] s2=[] s1.append(0) s2.append(0) s1.append(0) s2.append(0) for i in range(1, k): s1[1] = s1[1] + a[i] for i in range(2, k): s1.append(s1[i-1] - a[i-1]) s2.append(s2[i-1] + a[i-1]) # Ищем минимальное значение mn=sm for i in range(2, k): sm = sm - s1[i] + s2[i] mn=min(mn, sm) print(mn)
Переменная k — это количество приёмных пунктов (Т.е. длина массива a). Превая ячейка соответсвует приёмному пункту под номером 1, вторая ячейка под номером 2 и т.д. Само значение для k мы смотрим в конце файла. Например, для файла A значение напишем 999. Всего 998 приёмных пунктов, но т.к. индексы в массиве начинаются с 0, то мы должны завести 999 ячеек. Т.е. нулевая ячейка не будет никак задействована. Для файла B устанавливаем k в 9999995.
В сами ячейки массива мы поместим для каждого приёмного пункта количество контейнеров. Их легко вычислить. Если количество пробирок не нулевое, то мы должны это количество разделить на 36 и округлить в большую сторону. Количество контейниров в нашей программе для каждого приёмного пункта — это переменная z.
Пусть лаборатория расположена в первом пункте. Тогда вычислим для неё стоимость доставки:
sm1 = a[2]*1 + a[3]*2 + a[4]*3 + … + a[m]*(m-1)
Здесь m — это последний индекс массива a (m = k-1). Пусть лаборатория будет во втором пункте, тогда:
sm2= a[3]*1 + a[4]*2 + … + a[n]*(m-2) + a[1] = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]
Отсюда мы понимаем, что достаточно вычислить стоимость доставки sm1 по формуле, которую нам дали в задаче, только один раз для первого пункта. Для второго пункта вычисляем: sm2 = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]. Для третьего sm3 = sm2 — (a[3] + a[4] + … + a[m]) + a[2] + a[1] и т.д.
Значит, для каждого приёмного пункта i мы должны иметь уже готовую вспомагательную сумму s1[i] = a[i] + a[i+1] + …+ a[m], а так же сумму s2, т.е. сумма элементов, которые идут левее i (само a[i] уже не берётся): s2[i] = s[1] + s[2] + … + s[i-1].
Сумму s1[i] мы должны отнимать, а s2[i] прибавлять. По мерее продвижения по нашим приёмным пунктам, s1[i] будет уменьшаться, а s2[i] увеличиваться.
Но вспомогательные суммы s1[i] и s2[i] нужно тоже вычислисть, как можно эффективней. Достаточно вычислить для s1[1] и s2[1] (для первого приёмного пункта), а дальше можно воспользоваться закономерностью: s1[2] = s1[1]-a[1], s1[3] = s1[2]-a[2]…и т.д. Так же s2[2] = s[1]+a[1], s[3] = s[2]+a[2] и т.д.
s1[0] и s2[0] не нужны, они соответсвуют a[0], а она не используется при решении задачи. Значение s1[1] вычисляем «честно» с помощью цикла. Значение s2[1] = 0 (левее нет ячеек).
В самом первом цикле вычисляется значение для переменной sm — это стоимость перевозки, если лаборатория стоит в первом пункте. В последнем цикле программы вычисляем стоимоть для всех остальных приёмных пунктов, используя вышеописанные алгоритмы. И находим минимальное значение среди всех значений для переменной sm.
Ответ:
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Задания 24, 26 — файлы не скачиваются, а открываются текстом в новой вкладке браузера.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы — время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) |
ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1; 2 |
| 4 | 7 | 3 |
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Выполните задания, используя данные из файла ниже:
Задание 22
Источник: Демонстрационная версия ЕГЭ−2023 по информатике
2
В файле 22_1.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
3
В файле 22_2.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
4
В файле 22_3.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
5
В файле 22_4.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
Пройти тестирование по этим заданиям
Алгоритм решения
22 задания из ЕГЭ по информатике 2023г. с помощью Python.
1. Первоначально
копируем данные из файла Excel в блокнот (файл txt)
2. Создаем
массив: arr = [0]
, в который будем записывать максимальное время по процессам, а сами
номера процессов будут индексами этого процесса
3. Открываем
наш текстовый файл (путь к файлу прописываем):
f
= open(r‘C:UsersяDesktop0
Шкурин Д.НЕГЭЕГЭ 2023Задание 2222-25.txt‘)
4. Делаем
цикл по строкам (когда мы копировали в текстовый файл, у нас данные разделены
табуляцией s.split(‘t‘)):
for s
in f.readlines():
number, time, need = s.split(‘t’)
5.
Добавим нулевой элемент в массиве:
arr.append(0)
6. Делаем
цикл по номеру процесса, причем номер процесса (если их несколько «6;5;7;4;3»)
у нас разделен «;», что мы и учитываем need.split(‘;’):
for j in need.split(‘;’):
7.
Выбираем максимальный элемент нашего массива, причем мы из текста
делаем число int(number):
arr[int(number)] =
max(arr[int(number)], arr[int(j)])
8. Когда
выбрано максимальное значение процесса мы плюсуем к нему текущее значение
(потому что процессы связанные, один процесс может начаться только тогда, когда
предыдущий закончится):
arr[int(number)]
+= int(time)
9. Печатаем
максимальный элемент созданного нами массива, это и будет ответ:
print(max(arr))
А это наша
программа целиком:
arr = [0]
f = open(r’C:UsersяDesktop0 Шкурин Д.НЕГЭЕГЭ 2023Задание 2222-25.txt’)
for
s
in
f.readlines():
number, time, need = s.split(‘t‘)
arr.append(0)
for
j
in
need.split(‘;’):
arr[int(number)] = max(arr[int(number)], arr[int(j)])
arr[int(number)] += int(time)
print(max(arr))
Из урока Вы узнаете, как решать 22 задание ЕГЭ по информатике: дается подробное объяснение и разбор заданий по программированию циклов и ветвлений
Содержание:
- Объяснение задания 22 ЕГЭ по информатике
- Алгоритмизация и программирование: циклы и ветвления
- Решение 22 заданий ЕГЭ по информатике
- Работа с цифрами чисел в различных системах счисления
- Задания на алгоритм Евклида и поиск НОД
22-е задание: «Программирование: циклы и ветвления»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 7 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм, содержащий ветвление и цикл
До ЕГЭ 2021 года — это было задание № 20 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Технические ошибки при ответе на это задание часто обусловлены недостаточно аккуратным выполнением арифметических операций в недесятичных системах счисления»
ФГБНУ «Федеральный институт педагогических измерений»
Задание демонстрационного варианта 2022 года ФИПИ
Алгоритмизация и программирование: циклы и ветвления
* материал рассматривается на примере языка Pascal
Для решения 22 задания необходимо рассмотреть и повторить следующие темы:
- Условный оператор if
- Цикл while или repeat
- Цикл for со счетчиком
- Операция целочисленного деления div
- Операция взятия остатка mod
Алгоритм Евклида для вычисления НОД:
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны:
Пример:
Найти НОД 14 и 21 по алгоритму Евклида.
✍ Решение:
НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7) = НОД (7, 7) = 7
Реализация на Паскале:
1 2 3 4 5 6 7 |
function NOD (a, b: integer): integer; begin while a <> b do if a > b then a := a - b else b := b - a; NOD := a; end; |
Решение 22 заданий ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2021 года ФИПИ
Работа с цифрами чисел в различных системах счисления
22_1:
Ниже записан алгоритм.
Получив на вход число x, этот алгоритм печатает число L.
Укажите наибольшее нечетное число x, при вводе которого алгоритм печатает 53.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
var x, L, M, D: integer; begin readln(x); D:=x; L:=23; M:=141; while L<=M do begin L:=L+D; M:=M-3*D; end; writeln(L); end. |
Подобные задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
Pascal:
var x, L, M, D: longint; begin x := 1000; while true do begin D := x; L := 23; M := 141; while L <= M do begin L := L + D; M := M - 3 * D; end; if (l = 53) and (x mod 2 <> 0) then begin print(x); break; end; x -= 1; end; end.
✎ Аналитическое решение:
Разберем решение по одному из возможных вариантов выполнения данного задания.
Рассмотрим алгоритм:
- Результатом программы является вывод L.
- Цикл перестанет работать, когда L станет больше M (т.к.
while L<=M). - D в программе — это и есть искомый x (
D:=x;). - В цикле оператор
L:=L+Dработает, как сумматор: L накапливает в себе сумму всех D, тогда как D в нашей задаче не меняется и равна введенному x. - Сумматор (L) до цикла обычно обнуляется, сделаем это: т.е. в строке 5 вместо
L:=23представим, чтоL:=0. Тогда и условие задачи поменяется: т.е. вместо указанного в условии числа 53 программа выводит L равное 53-23 = 30. А в условии цикла M также изменит свое значение на 141-23=118: - Так как по заданию необходимо найти наибольший x, то представим, что он равен как раз 30:
1 2 3 4 5 6 7 8 9 10 |
... L:=23; M:=141; while L<=M do // L<=118 для первой итерации begin L:=L+D; M:=M-3*D; end; writeln(L); // выводится L = 30 end. |
L = L + D => L = 0 + 30 => L = 30
30 / 2 = 15
То есть D = x = 15
D=15 1 проход 2 проход L:=L+D: 0+15=15 15+15=30 M:=M-3*D: 118-3*15=73 73-3*15 = 28 L<=M: да: 15<=73 нет: 30 > 28
Результат: 15
📹 Подробное теоретическое решение данного задания 22 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
22_9:
Ниже записан алгоритм.
Получив на вход число x, этот алгоритм печатает число L.
Укажите наибольшее нечетное число x, при вводе которого алгоритм печатает 125.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
var x, L, M, D: integer; begin readln(x); D:=x; L:=17; M:=70; while L<=M do begin L:=L+2*D; M:=M+D; end; writeln(L); end. |
✍ Решение:
📹 Смотрите видео решения:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
22_2:
Ниже записан алгоритм. Получив на вход число x, этот алгоритм печатает S. Известно, что 100 ≤ x ≤ 200.
Укажите наибольшее допустимое число x, при вводе которого алгоритм распечатает 30.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
var x,A,B,D,S: integer; begin readln(x); B:= x; A:= 9; D:= x; S:= 0; while (D div 2)>0 do begin if (D mod 2) = 1 then S:= S + 1 else S:= S + A; D:= D div 2; end; writeln(S); end. |
Подобные задания для тренировки
✍ Решение:
-
Для начала рассмотрим алгоритм программы:
- В начале программы вводится x, две переменные — B и D присваивают значение введенного x. Переменной A присваивается значение 9, а переменная S обнуляется.
- Далее следует цикл, который зависит от переменной D (равной x): пока
x div 2 > 0выполняется тело цикла. Т.е. пока x, деленный целочисленно на 2, больше нуля. - В теле цикла происходит увеличение переменной
Sлибо на 9 (А:=9), либо на 1 в зависимости от четности значения D. Т.е. переменнаяSувеличивается на 9 в случае, если очередное значение D — четное и увеличивается на 1, если очередное значение D — нечетное. - В конце цикла D целочисленно делится на 2 (
D := D div 2). - По условию программы S должно быть равно 30. Посчитаем максимальное количество итераций цикла: 2n <= 200, т.е. n = 7 (максимальное значение D — 200 — делим целочисленно на 2, пока это возможно). При этом минимальное количество итераций — 6 (2n >=100, т.е. n = 6)
- За 7 или 6 итераций цикла необходимо получить S = 30, каждую итерацию цикла, увеличивая S либо на 1, либо на 9. Рассмотрим варианты:
- Из 6 итераций имеем: 3 итерации с D — нечетным (когда
s = s + 1) и 3 итерации с D — четным (когдаs = s + 9) - Четность чисел в двоичной системе счисления зависит от младшего бита: если младший бит = 0, то число четное, если 1, то число нечетное. Поскольку нам необходимо найти наибольшее x, то необходимо в трех старших битах данного числа, выраженного в двоичной системе счисления, поместить 1, а в остальных трех битах разместить 0. При этом необходимо не забыть про еще один старший бит равный 1 (в итерациях его нет, т.к. это последняя единица, которая уже не удовлетворяет условию цикла: условие цикла ложно while (1 div 2) > 0 — ложь):
30 = 9 + 9 + 9 + 1 + 1 + 1 -> (получаем 6 итераций, что соответствует действительности) 30 = 9 + 9 + 12 * 1 (если взять две девятки, то цикл должен работать 14 раз (9 + 9 + [12 единиц]), а это невозможно)
11110002 = 12010 первая единица будет стоять всегда, она не участвует в итерациях цикла Проверка: 120| 0 - соответствует s + 9 60| 0 - соответствует s + 9 30| 0 - соответствует s + 9 15| 1 - соответствует s + 1 7| 1 - соответствует s + 1 3| 1 - соответствует s + 1 1|
✎ 2 способ:
-
Рассмотрим алгоритм:
- Значение искомого x присваивается сразу двум переменным B и D, но B более нигде не используется, поэтому забудем про нее. D — это x.
D mod 2— это крайняя справа цифра числа в двоичной системе счисления (младший разряд); т.е.:
В цикле:
например, если D = 510 = 1012, то D mod 2 = 1 (101)
А = 9);D:= D div 2 — это отсечение крайнего младшего разряда числа D в двоичной системе счисления, т.е.:если было D = 510 = 1012, то стало D = 102
while (D div 2)>0);30 = 9 + 9 + 9 + 1 + 1 + 1 -> (получаем 6 итераций цикла)
111000
при оставшемся D = 1 условие while (1 div 2) > 0 не работает, поэтому добавляем еще старший разряд "1" таким образом, получаем число в двоичной системе: 1111000
64 32 16 8 4 2 1
1 1 1 1 0 0 0 = 64 + 32 + 16 + 8 = 12010
Результат: 120
Если что-то осталось непонятным, рекомендуем посмотреть разбор данного 22 задания на видео:
1-й длительный способ решения:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
2-й способ решения (простой и быстрый):
📹 YouTube здесь📹 Видеорешение на RuTube здесь
22_3:
Ниже записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M.
Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 8.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
var x,L,M: integer; begin readln(x); L:=0; M:=0; while x>0 do begin L:=L + 1; if M < (x mod 10) then M:=x mod 10; x:=x div 10; end; writeln(L);writeln(M); end. |
Подобные задания для тренировки
✍ Решение:
Рассмотрим алгоритм работы с L:
- В конце программы алгоритм выводит значение L, равное 2 (по условию). В цикле L — это счетчик, увеличивающийся каждую итерацию цикла (каждое прохождение цикла) на 1.
- Таким образом, цикл работает два раза.
- В цикле x постоянно уменьшается на 1 разряд, т.е. от него отсекается цифра справа (
x:=x div 10):
например, x = 243 после выполнения x:=x div 10 получаем х = 24
Рассмотрим работу с M в цикле:
- В первую итерацию цикла М всегда заменится на значение x mod 10, так как изначально М = 0.
- Из предыдущего пункта имеем, что M — это наименьшая цифра числа:
например, x = 243 после выполнения M := x mod 10; получаем 1 шаг: М = 3 2 шаг: М = 3 3 шаг: М = 2
Рассмотрим две цифры числа x путем подстановки:
- Поскольку по условию нам нужно наибольшее x, то попробуем в единицы записать число 8:
? 9
M < (x mod 10) не будет работать, и программа распечатает 9 (вместо 8). Т.е. 9 не походит:if M < (x mod 10) then
M:=x mod 10;
1 шаг:
if 0 < (9) then
M:=9;
2 шаг:
if 9 < (любая цифра) then ...
Условие не работает, программа распечатает М = 9. Не подходит!
? 8
if M < (x mod 10) then
M:=x mod 10;
1 шаг:
if 0 < (8) then
M:=8;
9 8
если она равна 9 (то есть число 98),
то М станет = 9 (а нам необходимо, чтобы осталось 8):
1 шаг:
if 0 < (8) then
M:=8;
2 шаг:
if 8 < 9 then ...
Условие работает, программа распечатает М = 9. Не подходит!
8 8
1 шаг:
if 0 < (8) then
M:=8;
2 шаг:
if 8 < 8 then ...
Условие не работает, программа распечатает М = 8. Подходит!
Результат: 88
📹 Но лучше один раз увидеть, как говорится. Посмотрите разбор задания на видео:
📹 YouTube здесь📹 Видеорешение на RuTube здесь
22_5: Демоверсия ЕГЭ 2018 информатика:
Ниже записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M.
Укажите наименьшее число x, при вводе которого алгоритм печатает сначала 5, а потом 7.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
var x, L, M: integer; begin readln(x); L := 0; M := 0; while x > 0 do begin M := M + 1; if x mod 2 <> 0 then L := L + 1; x := x div 2; end; writeln(L); writeln(M); end. |
Типовые задания для тренировки
✍ Решение:
-
Рассмотрим алгоритм:
- Наличие операторов
x mod 2иx div 2говорит о том, что эту задачу можно решать, представляя x в двоичной системе счисления. - В цикле есть счетчик M, который увеличивается на единицу и в конце программы будет соответствовать количеству итераций цикла. Таким образом, имеем 7 проходов цикла.
- Условие
if x mod 2 <> 0проверяет на нечетность младший разряд числа в двоичной системе:
В цикле:
например, если было x = 510 = 1012,
то if x mod 2 <> 0 проверяет if 1 <> 0
x := x div 2; отсекается младший разряд двоичного представления значения x, т.е.:если было, например, x = 510 = 1012, то стало x = 102
10011112 = 64 + 8 + 4 + 2 + 1 = 7910
✎ Способ 2 (длительный, аналитический):
- В начале программы вводится
x, и обнуляются две переменные —LиM. - Далее следует цикл, который зависит от переменной x: пока
x > 0выполняется тело цикла. - В теле цикла каждый его шаг происходит увеличение переменной M на единицу. Т.е. переменная M — это счетчик, соответственно, его значение по завершению работы цикла будет соответствовать количеству шагов (итераций) цикла.
- В конце программы печатается сначала L, потом M. Т.е. L должно быть равно 5, а M = 7. Раз M будет равно 7, то из предыдущего пункта видим, что цикл имеет 7 шагов, т.е. 7 итераций.
- L — это тоже счетчик, но из условия
if x mod 2 <> 0видим, что счетчик L подсчитывает количество нечетных промежуточных x. Т.е. x в цикле постоянно меняется, а L проверяет x и в случае нечетного значения увеличивается на единицу. В программе L должно стать 5. - В цикле x делится целочисленно на 2:
x := x div 2 - Поскольку цикл завершит работу, когда x = 0, то последним шагом будет
x = 1 div 2 = 0. Т.е. в предпоследнем шаге x = 1. - Решим данную задачу с конца, проследив все итерации цикла. Получается, что из предыдущего шага в следующий шаг x изменяется по двум правилам, назовем их командами:
Для начала рассмотрим алгоритм программы:
1. x*2 -> если предыдущий x - четный, например 4 div 2 - обратное действие 2*2 = 4 2. x*2+1 -> если предыдущий x - нечетный, например 5 div 2 - обратное действие 2*2+1 = 5
Результат: 79
Подробное решение 22 (20) задания демоверсии ЕГЭ 2018 года смотрите на видео:
Способ 1 (быстрый):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2 (аналитический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
22_6: Досрочный егэ по информатике 2018, вариант 1:
Укажите наибольшее десятичное число, при вводе которого на экране сначала напечатается 3, а затем 6.
1 2 3 4 5 6 7 8 9 10 11 12 |
var x, L, M: integer; begin readln(x); L:=0; M:=0; while x > 0 do begin L:=L + 1; if (x mod 2) <> 0 then M:= M + x mod 8; x:= x div 8; end; writeln(L); write(M); end. |
Типовые задания для тренировки
✍ Решение:
📹 Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
22_7:
Получив на вход натуральное десятичное число х, этот алгоритм печатает два числа: L и М.
Укажите наименьшее число х, при вводе которого алгоритм печатает сначала 42, а потом 4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
var x, L, M: integer; begin readln(x); L := 1; M := 0; while x > 0 do begin M := M + 1; if x mod 8 > 3 then L := L * (x mod 8); x := x div 8 end; writeln(L); writeln(M) end. |
✍ Решение:
-
Рассмотрим алгоритм:
- В конце программы на экран выводится сначала значение переменной L, затем M. Т.е. согласно заданию, получается что:
в конце программы: L = 42 M = 4
1. x mod 8 - младший разряд числа в 8-й системе счисления т.е., например: 568 тогда x mod 8 - это цифра 6 2. x := x div 8 - "отсекание" младшего разряда числа в 8-й системе счисления т.е., например: x = 4610 = 568 тогда x := x div 8 -> x = 510 = 58
if x mod 8 > 3 then проверяется каждая цифра числа: если она больше трех, то выполняется действие L := L * (x mod 8);. Дословно, это говорит о том, что L — это произведение цифр числа (в его 8-м представлении), которые больше трех.М = 4 - количество цифр числа т.е. x в 8-й системе счисления имеет 4 разряда: ? ? ? ? L = 42 произведение цифр, которые больше трех.
42 = 6 * 7
x = 10678
10678 = 56710
Результат: 567
22_8:
Укажите количество двузначных натуральных чисел, при вводе которых приведенная ниже программа напечатает число 0.
1 2 3 4 5 6 7 8 9 10 11 12 |
var i, n: longint; begin i := 0; readln(n); while (n > 0) do begin i := i + n mod 8; n := n div 8; end; writeln(i mod 7); end. |
✍ Решение:
-
✎Один из вариантов решения:
- В цикле while две операции указывают на то, что данное задание можно рассматривать при работе с числом в 8-й системе счисления:
1. n mod 8 - младший разряд числа в 8-й системе счисления т.е., например: 568 тогда n mod 8 - это цифра 6 2. n := n div 8 - "отсекание" младшего разряда числа в 8-й системе счисления т.е., например: n = 4610 = 568 тогда n := n div 8 -> n = 510 = 58
n mod 8 — младшая цифра числа, и каждую итерацию цикла от числа отсекается цифра младшего разряда, то на каждом шаге в i добавляется очередная справа цифра числа: Например: n = 2568 1) i := i + n mod 8; => i = 0 + 6 = 6 (256) 2) i := i + n mod 8; => i = 6 + 5 = 11 (256) 3) i := i + n mod 8; => i = 11 + 2 = 13 (256)
i mod 7, т.е. остаток от деления получившейся суммы на число 7.i - сумматор цифр введенного числа n в его восьмеричном представлении n - двузначные десятичные числа (по условию) результат программы = i mod 7 = 0, т.е. остаток от деления итоговой суммы на 7 (= 0)
nmin = 1010 = 128 nmax = 9910 = 1438
16 = 1+6 = 7 (7 mod 7 = 0), 25 = 2+5 = 7 (7 mod 7 = 0), 34 = 3+4 = 7 (7 mod 7 = 0), 43 = 4+3 = 7 (7 mod 7 = 0), 52 = 5+2 = 7 (7 mod 7 = 0), 61 = 6+1 = 7 (7 mod 7 = 0), 70 = 7+0 = 7 (7 mod 7 = 0), 77 = 7+7 = 14 (14 mod 7 = 0), 106 = 1+6 = 7 (7 mod 7 = 0), 115 = 1+1+5 = 7 (7 mod 7 = 0), 124 = 1+2+4 = 7 (7 mod 7 = 0), 133 = 1+3+3 = 7 (7 mod 7 = 0), 142 = 1+4+2 = 7 (7 mod 7 = 0),
Ответ: 13
22_10:
Получив на вход натуральное число x, этот алгоритм печатает два числа: a и b. Укажите наименьшее натуральное число, при вводе которого алгоритм печатает сначала 1, а потом 9.
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
var x, a, b: longint; begin readln(x); a := 0; b := 1; while x > 0 do begin if x mod 2 = 0 then a := a + x mod 9 else b := b * (x mod 9); x := x div 9; end; writeln(a); write(b); end. |
Бейсик:
INPUT x a=0: b=1 WHILE x>0 IF x MOD 2 = 0 THEN a = a + x MOD 9 ELSE b = b * x MOD 9 END IF x = x 9 WEND PRINT a PRINT b END |
Python:
x = int(input()) a = 0 b = 1 while x > 0: if x % 2 == 0: a = a + x % 9 else: b = b * (x % 9) x = x // 9 print(a) print(b) |
С++:
#include <iostream> using namespace std; int main() { int x, a, b; cin >> x; a = 0; b = 1; while (x > 0) { if (x%2 == 0) a += x%9; else b *= x%9; x = x / 9; } cout << a << endl << b; return 0; } |
✍ Решение:
-
Рассмотрим алгоритм.
- Программа получает на вход число x.
- В цикле, пока число x больше 0, в зависимости от того, четное ли число x выполняются действия:
- если четное, то в переменную a добавляется остаток от деления числа x на 9;
- если нечетное, то переменная b умножается на остаток от деления числа x на 9;
- x целочисленно делится на 9.
- Эти три действия в цикле — ни что иное, как работа с цифрами числа в 9-й системе счисления. Тогда, проверим значение x на четность в 9-й с.с.:
- если четное, то в переменную a добавляется крайняя справа цифра числа (остаток от деления числа x на 9);
- если нечетное, то переменная b умножается на крайнюю справа цифру числа x;
- x целочисленно делится на 9: значит, отсекаем от x в 9-й с.с. крайнюю справа цифру.
- Теперь попробуем подобрать наименьшее число x, рассматривая его пока в 9-й с.с.
if x mod 2 = 0 then a := a + x mod 9
Вспомним, что для систем счисления с нечётным основанием (наш случай, 9 — нечетное) справедливо утверждение, что число чётно тогда и только тогда, когда сумма всех его цифр чётна.
произведение цифр (b) должно быть равно 9 (если число x нечетное)
сумма цифр (a) должна быть равна 1 (если число x четное)
однозначное число: минимальное 9, но цифры 9 в 9-й с.с. нет. других вариантов получить 9 нет
двухзначное число: минимальное 33 3 + 3 = 6 (четное) => a = 0 + 3 = 3, не подходит (т.к. а=1) других вариантов получить 9 нет
трехзначное число: 1 случай: минимальное 133 1 + 3 + 3 = 7 (нечетное) => b = 1 * 3 = 3 отсекаем: x = 13 1 + 3 = 4 (четное) => a = 0 + 3 = 3, не подходит (т.к. а=1) 2 случай: следующее минимальное 313 3 + 1 + 3 = 7 (нечетное) => b = 1 * 3 = 3 отсекаем: x = 31 3 + 1 = 4 (четное) => a = 0 + 1 = 1 отсекаем: x = 3 3 (нечетное) => b = 3 * 3 = 9 отсекаем: x = 0, конец цикла
3139 = 3 * 92 + 1 * 9 + 3 = 25510
Ответ: 255
Предлагаем посмотреть видеоурок задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Задания на алгоритм Евклида и поиск НОД
22_4:
Ниже записан алгоритм. Получив на вход число x, этот алгоритм печатает число M.
Известно, что x>40. Укажите наименьшее такое (т.е. большее 40) число x, при вводе которого алгоритм печатает 5.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
var x,L,M: integer; begin readln(x); L:=x; M:=5; if L mod 2 = 0 then M:=24; while L <> M do if L > M then L:=L-M else M:=M-L; writeln(M); end. |
✍ Решение:
Рассмотрим алгоритм:
- В начале программы запрашивается x. Переменной L присваивается значение x, а переменной M — значение 5.
- Затем в условии проверяется четность переменной L: если переменная четная, то M присваивается значение 24.
- Далее следует цикл, зависящий от переменных L и M: цикл завершится, когда L сравняется с M, т.е. согласно условию, когда L = M = 5 (так как по завершению программы на экран выводится число 5):
По завершению программы: L = M = 5
НОД (a, b) = если a > b, то НОД (a-b, b) = если b > a, то НОД (a, b-a)
if L mod 2 = 0 не будет истинным, то в цикле постоянно будет происходить действие L:=L-M). Т.е. постоянно вычитается 5.L M 45 5 40 5 35 5 30 5 25 5 20 5 15 5 10 5 5 5
Результат: 45
Посмотрите видео-разбор данного задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
ЕГЭ информатика 22 задание разбор, теория, как решать.
Анализ программы с циклами и условными операторами, (П) — 1 балл
Е22.9 В файле содержится информация о вычислительных процессов проектов P1, Р2 и P3
(Е. Джобс) В файле содержится информация о вычислительных процессов проектов P1, Р2 и P3, которые могут выполняться параллельно или последовательно. Каждый вычислительный процесс разбивается на подпроцессы. Будем говорить, что подпроцесс B зависит от подпроцесса A, если для выполнения подпроцесса B необходимы результаты выполнения подпроцесса A внутри вычислительного процесса (Р1, Р2 или Р3). В этом случае …
Читать далее
Е22.8 процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно
(А. Кожевникова) В файле содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В …
Читать далее
Е22.7 В файле содержится информация о вычислительных процессов проектов P1 и P2
(Е. Джобс) В файле содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться только последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первой …
Читать далее
Е22.6 если для выполнения процесса B необходимы результаты выполнения процесса A
(В. Шубинкин) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.5 N вычислительных процессов, которые могут выполняться параллельно или последовательно
(Л. Евич) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.4 Будем говорить, что процесс B зависит от процесса A
(В. Шубинкин) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.3 Определите максимально возможное целочисленное t (время выполнения процесса)
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы …
Читать далее
Е22.2 Определите минимальное время, через которое завершится выполнение всей совокупности процессов
(Л. Евич) В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом …
Читать далее
Е22.1 В файле содержится информация о совокупности N вычислительных процессов
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы …
Читать далее
Канал видеоролика: Evgenij Jobs
Смотреть видео:
#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #поступление
Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):
С этим видео ученики смотрят следующие ролики:

Задание №1. Разбор демоверсии 2023 | Информатика ЕГЭ
Evgenij Jobs

Задание №2. Разбор демоверсии-2023 | Информатика ЕГЭ
Evgenij Jobs

Задание №3. Разбор демоверсии-2023 | Информатика ЕГЭ
Evgenij Jobs

Задание №4. Разбор демоверсии-2023 | Информатика ЕГЭ
Evgenij Jobs
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
31.08.2022
Автор материалов — Лада Борисовна Есакова.
Поиск количества программ по результату
Задачу такого типа можно решить, построив подробное дерево всех возможных вариантов наборов команд и подсчитав те, которые приведут к нужному результату. Однако, это очень длинный и объемный способ. Его использование может привести к вычислительным ошибкам, а при большой длине программы построение дерева вообще практически невозможно.
Рассмотрим более эффективный метод подсчета количества программ.
Пример 1.
У исполнителя Увеличитель две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 3.
Первая из них увеличивает число на экране на 2, вторая — умножает его на 3.
Программа для Увеличителя — это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 31?
Ответ обоснуйте.
Решение:
Заполним таблицу со следующими столбцами:
«Число» — перечень всех чисел от 1 до 31;
«Числа-источники» — числа, из которых одной из указанных команд можно получить текущее число;
«Количество способов» — количество способов, которыми можно получить текущее число из чисел-источников. Равно сумме значений «Кол-во способов» чисел-источников.
Заметим, что никаким набором указанных команд невозможно получить четное число из 1, значит, четные числа можем в таблице не рассматривать вообще.
|
Число |
Числа-источники |
Кол-во способов получения |
| 1 | 1 | 1 |
| 3 | 1 | 2 |
| 5 | 3 | 2 |
| 7 | 5 | 2 |
| 9 | 3 ; 7 | 2+2=4 |
| 11 | 9 | 4 |
| 13 | 11 | 4 |
| 15 | 5 ; 13 | 2+4=6 |
| 17 | 15 | 6 |
| 19 | 17 | 6 |
| 21 | 7 ; 19 | 2+6=8 |
| 23 | 21 | 8 |
| 25 | 23 | 8 |
| 27 | 9 ; 25 | 4+8=12 |
| 29 | 27 | 12 |
| 31 | 29 | 12 |
Число 1 нам дано, т.е. его можно получить единственным способом: ничего не делая.
Число 3 можно получить из 1 двумя способами: командой 1. и командой 2. И т.д.
Заметим, что два источника могут быть только у чисел, кратным трем. Это наблюдение поможет нам быстро заполнить таблицу, т.к. количество способов увеличивается, когда рассматриваем число, кратное трем.
Например, число 9 можно получить из числа 3 и числа 7. Сложив количество способов получения чисел 3 и 7 (2+2=4), получим количество способов получения числа 9.
Полная таблица приведена для наглядности, можно было заполнить только строки с числами, кратными 3, т.к. только они меняют количество способов получения числа.
Для числа 31 получаем количество способов 12. Это и есть искомое количество программ.
Ответ: 12
Пример 2.
У исполнителя Арифметик две команды, которым присвоены номера:
1. прибавь 1,
2. прибавь 3.
Первая из них увеличивает на 1 число на экране, вторая увеличивает это число на 3.
Программа для Арифметика — это последовательность команд.
Сколько существует программ, которые число 2 преобразуют в число 15?
Решение:
Заполним таблицу со следующими строками:
«Число» — перечень всех чисел от 2 до 15;
«Числа-источники» — числа, из которых одной из указанных команд можно получить текущее число;
«Количество способов» — количество способов, которыми можно получить текущее число из чисел-источников. Равно сумме значений «Кол-во способов» чисел-источников.
|
Число |
Числа-источники |
Кол-во способов получения |
| 2 | 2 | 1 |
| 3 | 2 | 1 |
| 4 | 3 | 1 |
| 5 | 2 ; 4 | 1+1=2 |
| 6 | 3 ; 5 | 1+2=3 |
| 7 | 4 ; 6 | 1+3=4 |
| 8 | 5 ; 7 | 2+4=6 |
| 9 | 6 ; 8 | 3+6=9 |
| 10 | 7 ; 9 | 4+9=13 |
| 11 | 8 ; 10 | 6+13=19 |
| 12 | 9 ; 11 | 9+19=28 |
| 13 | 10 ; 12 | 13+28=41 |
| 14 | 11 ; 13 | 19+41=60 |
| 15 | 12 ; 14 | 28+60=88 |
Для числа 15 получаем количество способов 88. Это и есть искомое количество программ.
Ответ: 88
Пример 3.
Исполнитель Май15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2.
Программа для исполнителя Май15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и при этом траектория вычислений содержит число 14 и не содержит числа 25? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решение:
Заполним таблицу со следующими строками:
«Число» — перечень всех чисел от 2 до 29;
«Числа-источники» — числа, из которых одной из указанных команд можно получить текущее число;
«Количество способов» — количество способов, которыми можно получить текущее число из чисел-источников. Равно сумме значений «Кол-во способов» чисел-источников.
|
Число |
Числа-источники |
Кол-во способов получения |
| 2 | 2 | 1 |
| 3 | 2 | 1 |
| 4 | 2 ; 3 | 1+1=2 |
| 5 | 4 | 2 |
| 6 | 3 ; 5 | 1+2=3 |
| 7 | 6 | 3 |
| 8 | 4 ; 7 | 2+3=5 |
| 9 | 8 | 5 |
| 10 | 5 ; 9 | 2+5=7 |
| 11 | 10 | 7 |
| 12 | 6 ; 11 | 3+7=10 |
| 13 | 12 | 10 |
| 14 | 7 ; 13 | 3+10=13 |
| 15 | 14 | 13 |
| 16 | 15 | 13 |
| 17 | 16 | 13 |
| 18 | 17 | 13 |
| 19 | 18 | 13 |
| 20 | 19 | 13 |
| 21 | 20 | 13 |
| 22 | 21 | 13 |
| 23 | 22 | 13 |
| 24 | 23 | 13 |
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | 14 | 13 |
| 29 | 28 | 13 |
До строки с числом 15 считаем все способы получения чисел. Начиная с числа 16 и до числа 24 (включительно) числа-источники 8-12 и способ получения числа применением команды «Умножить на 2» не подходят, т.к. траектория вычисления не содержит число 14. Для этих чисел учитываем одно число-источник (предыдущее) и один способ получения – «Прибавить 1».
Числа 25 вообще не должно быть в траектории, а значит, числа 26 и 27 получить невозможно.
Для числа 28 существует одно число-источник (14).
Для числа 29 получаем количество способов 13. Это и есть искомое количество программ.
Ответ: 13
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №22. Перебор вариантов.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023