Здравствуйте! Сегодня речь пойдёт о 23 задании из ЕГЭ по информатике 2023.
Двадцать третье задание является последним заданием из первой части ЕГЭ по информатике 2023.
Давайте познакомимся с примерными задачами 23 задания из ЕГЭ по информатике 2023.
Задача (классическая)
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавить 3,
2. умножить на 2.
Первая из них увеличивает число на экране на 3, вторая — удваивает его.
Программа для Удвоителя — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 25 ?
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+3, y) + F(x*2, y) print(F(1, 25))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
Ответ получается равен 9.
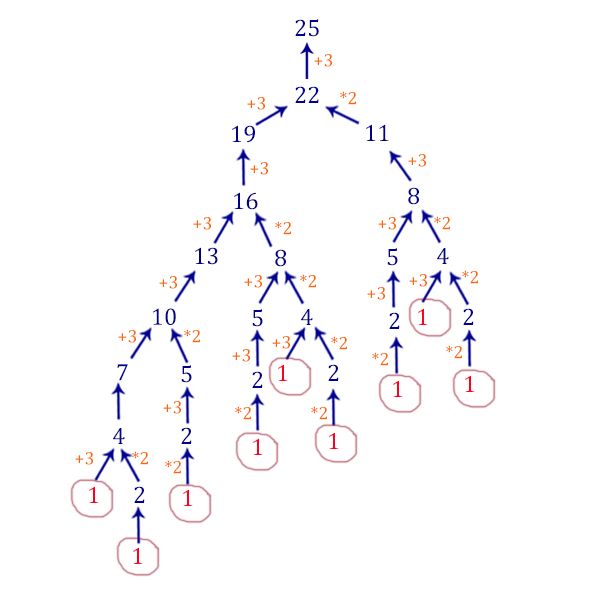
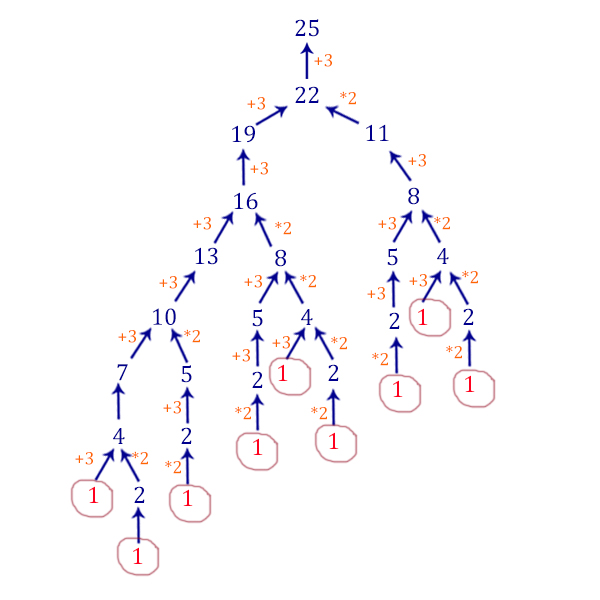
2 Способ (графический, для понимания)
Начинаем рассматривать задачку с конца. Если число нечётное, то оно может быть получено только с помощью первой команды. Если число чётное, то оно может быть получено с помощью двух команд.
Видим, что количество программ получается 9!
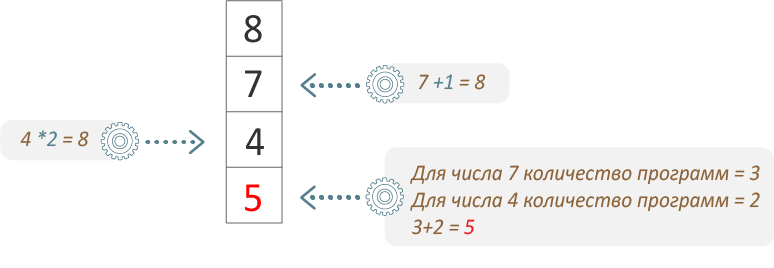
3 Способ (С помощью таблицы)
Некоторое число i можно получить только двумя способами: либо c помощью первой команды, либо с помощью второй команды. Тогда количество программ для некоторого числа i будет складываться из двух чисел: количества программ для числа i-3 и количества программ для числа i / 2 (Если i — чётное).
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| *2 | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 |
| Кол. Прог. |
1 | 1 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 3 |
| Числа | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| +3 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| *2 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | — |
| Кол. Прог. |
3 | 0 | 3 | 5 | 0 | 6 | 5 | 0 | 6 | 8 | 0 | 9 | 8 | 0 | 9 |
В первой строке пишутся числа от 1 до 25 (до того числа, которое нужно получить).
Во второй строке пишутся числа, которые в сумме с 3 (тройкой) дают числа, написанные в первой строке. (Прим. начиная с 4, числа идут по порядку.)
В третьей строке пишутся числа, которые при умножении на 2 дают числа, написанные в первой строке. (Прим. числа так же идут по порядку через одну пустую ячейку.)
В четвёртой строке для единицы ставим 1. Для остальных ячеек: смотрим, какие числа участвуют во второй и третьей строке для конкретной ячейки. Затем, эти числа ищем в первой строке и пишем сумму количеств программ для этих чисел (Т.е. пишем сумму уже известных значений из четвёртой строки для этих чисел).
Таким образом, основная идея 23 задания из ЕГЭ по информатике заключается в том, что результат каждого шага опирается на результаты предыдущих шагов!
Получаем ответ 9!
Ответ: 9
Задача (с избегаемым узлом)
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ — это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y or x==24: return 0 if x < y: return F(x+1, y) + F(x*2+1, y) print(F(1, 25))
Здесь на нельзя получать число 24, поэтому, если x будет равен 24, то мы возвращаем ноль.
Ответ получается равен 10.
2 способ (Решение с помощью таблицы).
Мы не может получать число 24! Значит, единственным способом добраться до числа 25 будет вторая команда.
Получается, что сначала нужно получить число 12, тогда 2 * 12 + 1 = 25 (2x+1). Это единственный путь!
Каждое число можем получить только 2 способами (Либо с помощью первой команды, либо с помощью второй команды). Поэтому количество программ для некоторого числа i будет равно сумме количеств команд для числа i-1 и для числа (i — 1) / 2 (Если число нечётное.) Если число i — чётное, то до числа i можно добраться единственным способом (с помощью первой команды).
Если записать с помощью массива:
A[i]=A[i-1] — если i — четное.
A[i]=A[i-1] + A[(i-1)/2] — если i нечетное;
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2x+1 | — | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол. Прог. |
1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 7 | 7 | 10 | 10 |
Ответ: 10
Задача (ЕГЭ по информатике, Москва, 2019)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает его на 2.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит число 9 и число 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(2, 9)*F(9, 11)*F(11, 12))
У нас числа 9 и 1 обязательные, поэтому разбиваем функцию следующим образом F(2, 9)*F(9, 11)*F(11, 12), через умножение. Это и будет ответ. Получается 50.
2 способ (с помощью таблицы).
От числа 11 до числа 12 можно добраться единственным путём (11 + 1 = 12).
От числа 9 до числа 11 можно добраться двумя способами (9 + 1 + 1 = 11, 9 + 2 = 11).
Найдём сколькими способами можно попасть от числа 2 до числа 9.
| Числа | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| +1 | — | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| *3 | — | — | — | — | 2 | — | — | 3 |
| +2 | — | — | 2 | 3 | 4 | 5 | 6 | 7 |
| Кол-во программ |
1 | 1 | 2 | 3 | 6 | 9 | 15 | 25 |
Учитывая, что от 9 до 11 двумя способами можно добраться, то 25 * 2 = 50 — это и будет ответ.
Ответ: 50
Задача ( ЕГЭ по информатике, Москва, 2020)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает на 2.
Сколько существует программ, которые преобразуют исходное число 3 в число 14 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(3, 9)*F(9, 14))
Ответ получается 112.
2 способ (с помощью таблицы).
Последней командой для получении любого числа из траектории программы может быть одна из трёх выше указанных команд!
Значит, количество программ для некоторого числа будет складываться из количества программ для тех чисел, из которых это число может быть получено.
Получается, что мы будем использовать основной принцип 23 задания из ЕГЭ по информатике: результат для некоторого числа опирается на результаты предыдущих чисел. Т.к. траектория вычислений программ обязательно должна проходить через число 9, то при вычислении результата для чисел больших 9, мы не можем опираться на результаты для чисел меньших 9 (Иначе мы пропустим число 9).
| Числа | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| +1 | — | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| *3 | — | — | — | — | — | — | 3 | — | — | — | — | — |
| +2 | — | — | 3 | 4 | 5 | 6 | 7 | — | 9 | 10 | 11 | 12 |
| Кол-во программ |
1 | 1 | 2 | 3 | 5 | 8 | 14 | 14 | 28 | 42 | 70 | 112 |
Ответ: 112
Посмотрим следующую задачу из 23 задания ЕГЭ по информатике 2023
Задача (с обязательным узлом, закрепление)
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x+3, y) print(F(1, 9)*F(9, 17))
Ответ получается 169.
2 способ (с помощью таблицы).
Любое число может получится в результате двух команд! Тогда количество программ для числа i будет складываться из количеств команд для числа i — 1 и для числа i — 3.
Если написать на языке массива
A[i] := A[i-1] + A[i-3], при i > 3.
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | — | — | 9 | 10 | 11 | 12 | 13 | 14 |
| Кол-во программ |
1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 13 | 13 | 26 | 39 | 52 | 78 | 117 | 169 |
При составлении значения для числа 10, мы не имеем право «заглядывать» за число 9, иначе число 9 будет пропущено! Поэтому для следующих трёх чисел (9, 9 + 1, 9 + 1 + 1), начиная с 9, будет 13 программ.
Для числа 17 получается ответ 169.
Ответ: 169
28.06.2021
2 комментария
Р-07. Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и при этом траектория вычислений содержит число 14 и не содержит числа 25?
Решение (электронные таблицы Excel, LibreOffice Calc с помощью функции ИНДЕКС):
- Основная идея решения заключается в том, что количество программ для данного числа равно сумме аналогичных значений чисел, в которые можно попасть из данного с помощью команд
- будем использовать возможность функции ИНДЕКС возвращать значение из ячейки, адрес которой можно вычислить. Для этого функции надо знать диапазон, в котором брать значения и номер строки и столбца внутри диапазона
- поскольку траектория содержит число 14, разобьем решение на два этапа
- найдем количество программ, для которых при исходном числе 2 результатом будет 14. В столбец А внесем числа от 2 до 14 так, чтобы каждое число совпадало с номером строки
- в столбец B внесем формулу для подсчета количества программ. В ячейке B2 это будет формула =ИНДЕКС(B$1:B$100;A2+1)+ИНДЕКС(B$1:B$100;A2*2)
- в функции ИНДЕКС(B$1:B$100;A2+1) B$1:B$100 это диапазон, внутри которого мы будем брать значения. Начинаться он должен с первой строки для того, чтобы нумерация строк внутри диапазона совпала с нумерацией чисел при вычислениях. А заканчиваться в такой ячейке, номер которой позволит взять любое число. В данном случае для расчета количества программ для числа 13 надо взять значения чисел 14 и 26. Значит, диапазон должен включать хотя бы 26 строк. Число 100 взято с запасом. Абсолютная адресация позволит эту формулу скопировать в другие ячейки стоблца B. A2 + 1 это вычисление из какой строки надо взять данные. По условию задачи у нас две команды: +1 и *2, соответственно, для подсчета количества программ в ячейке B2, которая соответствует числу 2, мы возьмем числа из строк 2 + 1 = 3 и 2 * 2 = 4
- данную формулу мы копируем на ячейки диапазона B3:B13, а в ячейку B14 внесем 1
- вторая часть решения – количество программ из 14 в 29. Построим данную часть правее, в столбцах С и D. Для корректной работы функции ИНДЕКС с формулами важно числа писать в совпадающие по номеру строки, а диапазон в формуле начинать с первой строки. Внесем формулу =ИНДЕКС(D$1:D100;C14+1)+ИНДЕКС(D$1:D100;C14*2) в ячейку D14, скопируем ее до ячейки D28, а в ячейку D29 внесем 1. Для того, чтобы учесть, что в 25 нельзя, просто удалим значение в столбце D напротив 25
- в ячейке B2 получилось количество программ, которыми можно попасть из 2 в 14, а в ячейке D14 количество программ из 14 в 29 минуя 25. Для получения итогового ответа перемножим эти числа: 13*1=13
- Ответ: 13
Подробнее о методе решения https://youtu.be/bHUpKN8iftA
На уроке рассмотрен разбор 23 задания ЕГЭ по информатике: дается подробное объяснение и решение заданий демоверсий и досрочных вариантов разных годов
23-е задание: «Динамическое программирование и анализ работы алгоритма»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 8 минут.
Проверяемые элементы содержания: Умение анализировать результат исполнения алгоритма
До ЕГЭ 2021 года — это было задание № 22 ЕГЭ
Рекомендации по выполнению:
«Один из распространенных способов выполнения этого задания – выписать последовательность
рекуррентных формул, определяющих, сколькими способами можно получить текущее число из ближайших предшественников, одновременно производя вычисления по этим формулам. «Ближайших» в данном случае означает тех, из которых текущее число получается в результате применения программы, состоящей из одной команды. Когда текущее число сравняется с заданным, количество таких способов и будет искомым числом программ»
Типичные ошибки и рекомендации по их предотвращению:
«Не стоит пытаться перечислить все пути в явном виде, это слишком трудоёмко и, скорее всего, в итоге приведёт к ошибке. Распространённая ошибка – экзаменуемые в процессе рекуррентных вычислений забывают о том, что траектория обязана содержать или не содержать указанные в условии числа»
ФГБНУ «Федеральный институт педагогических измерений»
Объяснение темы «Динамическое программирование»
- Динамическое программирование – это способ или техника решения сложных задач путем приведения их к более простым подзадачам того же типа.
- Динамическое программирование позволяет решать задачи, которые требуют полного перебора вариантов. Задание может звучать так:
- «подсчитайте количество способов…»;
- «как оптимально распределить…»;
- «найдите оптимальный маршрут…».
- Динамическое программирование позволяет увеличить скорость выполнения программы за счет эффективного использования памяти; полный перебор всех вариантов не требуется, поскольку запоминаются и используются решения всех подзадач с меньшими значениями параметров.
Более подробное знакомство с динамическим программированием доступно по ссылке.
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
23_4: Разбор досрочного ЕГЭ по информатике 2019:
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
Сколько существует программ, для которых при исходном числе 3 результатом является число 37 и при этом траектория вычислений содержит число 18?
✍ Решение:
📹 Подробный разбор смотрите на видео:
📹 YouTube здесь📹 Видеорешение на RuTube здесь
23_2:
У исполнителя Увеличитель две команды, которым присвоены номера:
- прибавь 1
- умножь на 4
Первая из них увеличивает число на экране на 1, вторая умножает его на 4.
Программа для Увеличителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 44?
✍ Решение:
- Возьмем такое наименьшее число, находящееся в интервале от 3 до 44, для которого применима только одна команда:
12 к нему применима только команда - прибавь 1 12 * 4 = 48 - это больше, чем 44
Пояснение: Красным цветом будем выделять количество команд для получения конкретного числа, а в круг обводить итоговое суммарное количество команд.
Пояснение: поскольку это задача динамического программирования, то полученные промежуточные результаты, используются для дальнейших вычислений:
- для 11 взят результат, полученный для 12 (1);
- для 10 взят результат, полученный для числа 11 (2);
- для 9 взят результат, полученный для 10 (3);
- и т.д.
Результат: 10
📹 Предлагаем посмотреть видео с решением данного 23 задания (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретический способ)
23_3: Демоверсия ЕГЭ 2018 информатика:
Исполнитель М17 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд.
Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 24, 26.
✍ Решение:
- Изобразим траекторию в виде луча, на котором отложим отрезки:
- Поскольку 8 и 10 обязательно должны содержаться в расчете, то для поиска общего количества программ необходимо найти произведение количества программ отдельных отрезков:
1 * 2 * 3 или (2 -> 8) * (8 -> 10) * (10 -> 12)
2 -> 8 = 157 7 + 1 = 8 7 + 2 = 9 - нельзя, вне интервала
8 -> 10 = 210 -> 12 = 215 * 2 * 2 = 60
Результат: 60
📹 Подробное решение 23 (теоретическое) задания демоверсии ЕГЭ 2018 доступно на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Канал видеоролика: ГИА по информатике
Смотреть видео:
#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #подготовкакэкзаменам
Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):
С этим видео ученики смотрят следующие ролики:

ЕГЭ по информатике. Решение 23 задания в электронных таблицах в одну формулу (дополнение)
ГИА по информатике

Решение задания №1. Демо ЕГЭ по информатике — 2021
ЕГЭ по информатике

Решение задания №2. Демо ЕГЭ по информатике — 2021
ЕГЭ по информатике

Решение задания №3. Демо ЕГЭ по информатике — 2021
ЕГЭ по информатике
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
27.05.2021
В 2021 году экзамен по информатике кардинально изменился. Теперь он проходит в компьютерной форме. Полностью исчезли задания, требующие простого воспроизведения формул и терминов. В ЕГЭ нового типа нужно рассуждать и решать задачи. Часть выполняется на бумаге, в электронную форму вносится только ответ. Другая часть представляет собой работу в компьютерных программах. Изменения коснулись и номера 23 из ЕГЭ по информатике. Раньше это была задача на системы логических уравнений, которая вызывала у школьников затруднения. В нынешнем году ее убрали, заменив на вопрос с анализом результата исполнения алгоритма. Он относится к первой части и дает 1 балл. Разбираемся в теории и решении 23 задания в ЕГЭ по информатике.
Теория
Задача 23 связана с алгоритмами. Алгоритм — полное и точное описание действий, приводящее к конечному результату. В информатике исходными и выходными данными является информация. Алгоритмы реализуются в компьютерных программах, они должны занимать определенный объем памяти и время. Алгоритм должен быть:
дискретным (прерывным). Состоит из последовательности простых шагов;
- детерминированным (определенным). В описании операций нет многозначности, исполнитель понимает их и может реализовать;
- массовым. Позволяет решить не одну задачу, а группу аналогичных. В качестве возможных данных используются переменные;
- результативным. Рассматривает все ситуации, дает конечный результат;
- конечным. Имеется определенное количество шагов;
- эффективным. Время выполнения алгоритма позволяет использовать его для реальных задач.
Алгоритм делят на базовые элементы (структуры). Структуры бывают трех типов: следование (последовательные действия), ветвление (программа проверяет условие и выбирает один из вариантов действия в зависимости от результата), цикл (несколько действий повторяются многократно). В задании 23 по информатике используются следующие способы записи алгоритмов:
- обычный язык. Текст с разделением на шаги;
- блок-схема. Программа представляется графически, используются специальные блоки:
|
Блок |
Обозначение |
|
|
Начало, конец |
|
Ввод, вывод данных |
|
|
Операция |
|
|
Условие |
|
|
Цикл с параметром |
|
|
Обращение к дополнительным алгоритмам |
- Блок
- Обозначение
- Начало, конец
- Ввод, вывод данных
- Операция
- Условие
- Цикл с параметром
- Обращение к дополнительным алгоритмам
- языки программирования. Имеют строгие правила записи, включающие в себя символы и зашифрованные слова;
- псевдокод. Объединение обычного языка и языка программирования. Нет строгих правил, но есть неизменяемые слова, задающие алгоритм. Например, «нач» — начало, «кон» — конец, «рез» — результат.
Примеры из ЕГЭ
Чтобы хорошо подготовиться к экзамену, нужно решить практические задачи по 23 заданию. Номер основан на динамическом программировании — решении сложных задач путем приведения к более простым. То есть, для выполнения конечного алгоритма нужно разобраться с подзадачами.
Для решения могут применяться графический и табличный способ.
Пример 1. У исполнителя Удвоитель две команды:
1. прибавить 3
2. умножить на 2
Программа для Удвоителя — последовательность команд.
Сколько есть программ, преобразующих число 1 в 25?
Решение. Решим графическим способом. Начнем выполнять с конца. Итоговый результат получается двумя способами — прибавлением к числу Х тройки или умножением числа Y на 2. 25 — нечетное число, вариант с умножением отпадает. Следовательно, перед 25 в алгоритме стояло 25-3=22.
Число 22 получается и умножением, и сложением. Алгоритм разделяется на 2: в одном число 22:2=11, а в другом 22-3=19. Каждое из этих чисел анализируем по той же схеме. Нужно «разворачивать» алгоритм до тех пор, пока каждая из ветвей не закончится единицей. Рисунок выглядит так:
Ответ: 9.
Пример 2. Исполнитель Вычислитель преобразует число, записанное на экране. У исполнителя есть две команды:
1. прибавить 1
2. умножить на 2
Сколько существует программ, преобразующих исходное число 2 в число 9?
Решение. Воспользуемся таблицей. В этом случае решаем в прямом порядке. В первой строке таблицы записываем все целые числа от исходного до итогового. Во второй пишем число, к которому нужно прибавить 1 для получения цифры из первой строки. В третьей строке аналогично, но с умножением. Четвертая строка — количество разных команд, которые могут привести к получению числа.
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
+1 |
— |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
•2 |
— |
— |
2 |
— |
3 |
— |
4 |
— |
|
Кол-во программ |
1 |
1 |
2 |
2 |
3 |
3 |
5 |
5 |
На примере восьмерки:
Ответ: 5.
Итак, мы изучили теорию 23 номера и провели его разбор. Конечно, это непростое задание, и далеко не все могут понять его самостоятельно. Если оно показалось вам сложным, можно записаться на курсы подготовки к ЕГЭ, где о выполнении задач будут рассказывать опытные преподаватели. А мы желаем вам удачи в сдаче ЕГЭ и поступлении в вуз!
Всего: 319 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 …
Добавить в вариант
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 3 | 5 | |
| 2 | =2*C1–B1–2*A1 | =C1+A1–2 | =(C1–9)* B1–2 |
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 08.07.2013. Вторая волна. Вариант 802.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 12 | =A1*4 | |
| 2 | =B1/A1 | =C1/B1 | =B2 + A1/6 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 15 | =A1*25 | |
| 2 | =B1/A1 | =C1/B1 | =B2+A1/3 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 3 | 5 | |
| 2 | =2C1−11 | =C1+1 | =B1(C1−A1*3)−2 |
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 11 | =A1*2 | |
| 2 | =(B1−A1)/2 | =B1−C1 | =B2+A1 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 7 | =A1*2 | |
| 2 | =(B1−A1)/2 | =B1−C1 | =B2+A1 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 6 | 25 | |
| 2 | =A1 − C1 | =B1/(A1-C1) | =A1 + 4*C1 |
Какое целое число должно быть записано в ячейке C1, чтобы диаграмма, построенная после выполнения вычислений по значениям диапазона ячеек A2:С2, соответствовала рисунку? Значения во всех ячейках диапазона A1:C2 одного знака.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 9 | 36 | |
| 2 | =A1−C1 | =B1/(A1-C1) | =A1+C1 |
Какое целое число должно быть записано в ячейке C1, чтобы диаграмма, построенная после выполнения вычислений по значениям диапазона ячеек A2:С2, соответствовала рисунку? Значения во всех ячейках диапазона A1:C2 одного знака.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 1 | 3 | |
| 2 | =A1+2*B1+1 | =C1–A1 | =(C1+A1)/2 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 1.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 3 | 2 | |
| 2 | =A1–C1 | = 4*C1–A1 | =3*(B1+C1)/A1 |
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная после выполнения вычислений по значениям диапазона ячеек A2:С2, соответствовала рисунку? Значения во всех ячейках диапазона A1:C2 одного знака.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 3 | 2 | |
| 2 | =A1–C1 | =6*C1–A1 | =5*(B1+2*C1)/A1 |
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная после выполнения вычислений по значениям диапазона ячеек A2:С2, соответствовала рисунку? Значения во всех ячейках диапазона A1:C2 одного знака.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 1 | 6 | |
| 2 | =A1+B1/2 | =(1+A1+B1)/4 | =(C1–1)*2 |
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 2.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 4 | 6 | |
| 2 | = (A1 − 2)/(B1 − 1) | = C1*B1/(4*A1 + 4) | = C1/(A1 − 2) |
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Источник: Демонстрационная версия ЕГЭ—2015 по информатике.
Дан фрагмент электронной таблицы.
| A | B | C | |
| 1 | 4 | 10 | |
| 2 | = (C1 – 5)/(4*A1) | = 1/(C1 + 1) | = 3/(2*C1 + B1) |
Какое целое число должно быть записано в ячейке С1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Источник: ЕГЭ по информатике 23.03.2016. Досрочная волна
В ячейки электронной таблицы записаны числа, как показано на рисунке:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 100 | 1001 | 2001 | 1001 | ||
| 2 | 200 | 2001 | 4000 | 2001 | ||
| 3 | 400 | 3001 | 6001 | 3001 | ||
| 4 | 800 | 4001 | 8000 | 4001 | ||
| 5 | 1600 | 5001 | 10001 | 5001 | ||
| 6 | 3200 | 6001 | 12000 | 6001 |
В ячейку A4 записали формулу =$D2+E$2. Затем ячейку A4 скопировали в одну из ячеек диапазона A1:B6, после чего в этой ячейке появилось числовое значение 6002. В какую ячейку выполнялось копирование?
Примечание: знак $ обозначает абсолютную адресацию.
В ячейки электронной таблицы записаны числа, как показано на рисунке:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 100 | 1001 | 2001 | 1001 | ||
| 2 | 200 | 2001 | 4000 | 2001 | ||
| 3 | 400 | 3001 | 6001 | 3001 | ||
| 4 | 800 | 4001 | 8000 | 4001 | ||
| 5 | 1600 | 5001 | 10001 | 5001 | ||
| 6 | 3200 | 6001 | 12000 | 6001 |
В ячейку B3 записали формулу =$D4+E$4. Затем ячейку B3 скопировали в одну из ячеек диапазона A1:B6, после чего в этой ячейке появилось числовое значение 6002. В какую ячейку выполнялось копирование?
Примечание: знак $ обозначает абсолютную адресацию.
В ячейки электронной таблицы записаны числа, как показано ниже:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 20 | 30 | 40 | 50 | 60 |
| 2 | 70 | 80 | 90 | 100 | 200 | 300 |
| 3 | 400 | 500 | 600 | 700 | 800 | 900 |
| 4 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 |
| 5 | ||||||
| 6 |
В ячейку B5 записали формулу =$D2+B$4. Затем ячейку B5 скопировали во все ячейки диапазона A5:F6. Какое наибольшее числовое значение появится в ячейках этого диапазона?
Примечание: знак $ обозначает абсолютную адресацию.
В ячейки электронной таблицы записаны числа, как показано ниже:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 20 | 30 | 40 | 50 | 60 |
| 2 | 70 | 80 | 90 | 100 | 200 | 300 |
| 3 | 400 | 500 | 600 | 700 | 800 | 900 |
| 4 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 |
| 5 | ||||||
| 6 |
В ячейку С6 записали формулу =$B2+C$3. Затем ячейку C6 скопировали во все ячейки диапазона A5:F6. Какое наибольшее числовое значение появится в ячейках этого диапазона?
Примечание: знак $ обозначает абсолютную адресацию.
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Источник: Демонстрационная версия ЕГЭ−2021 по информатике
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
18.xlsx
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Ответ:
Источник: ЕГЭ по информатике 2022. Досрочная волна
Всего: 319 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 …
Характеристика задания
1. Тип ответа: запись числового выражения.
2. Структура содержания задания: задан алгоритм на формальном языке.
3. Уровень сложности: повышенный.
4. Примерное время выполнения: (8) минут.
5. Количество баллов: (1).
6. Требуется специальное программное обеспечение: да.
7. Задание проверяет умение анализировать результат исполнения алгоритма, содержащего ветвление и цикл, с помощью языка программирования.
Пример задания (демоверсия ЕГЭ (2023))
Рис. (1). Пример задания
Для начала рассмотрим более лёгкое аналогичное задание.
У исполнителя Калькулятор три команды, которым присвоены номера:
1) прибавь (1);
2) умножь на (2);
3) умножь на (3).
Сколько существует программ, которые число (1) преобразуют в число (6)?
Решить такую задачу можно следующими способами:
1) построить дерево;
2) построить таблицу вариантов;
3) с помощью языка программирования.
Рис. (2). Дерево
Способ (2)
Чтобы определить количество программ, нужно рассмотреть условия:
1) прибавь (1);
2) умножь на (2);
3) умножь на (3).
Построим таблицу. Условия получения чисел будут таковы:
если число не делится ни на (2) и ни на (3), то количество вариантов вычисляется по формуле
KN=KN
−1
(т. е равно предыдущему значению) ((1)).
Если число делится только на (2), то количество вариантов вычисляется по формуле
Если число делится только на (3), то количество вариантов вычисляется по формуле
Если число делится и на (2), и на (3), то количество вариантов вычисляется по формуле
((4)).
Построим таблицу, в верхней строке будем писать числа (N), которые нужно получить, а в нижней строке — количество команд (N), которые мы получаем.
Рис. (3). Таблица
Способ (3)
Разработаем программу, которая определит результат. В программе используем функцию, которая будет возвращать значения при определённых условиях.
Какие условия нужно рассмотреть?
| 1 |
Объявим функцию (F), переменная (x) — первое число (из которого нужно начать работу), (y) — второе число, которое нужно получить |
|
1 2 |
Проверим условие: если (x) окажется больше (y), то команд получения из одного числа другого нет, т. е. (0) |
|
1 2 3 |
Проверим условие: если (x) равно (у), то команда есть, и она одна, поэтому возвращаем (1) команду |
|
1 2 3 4 |
Данная строка возвращает значение функции. Как видим, в записях «(x + 1)», «(x*2)», «(x*3)» заложены условия задания: 1) прибавь (1); 3) умножь на (3) |
|
1 2 3 4 5 |
Вызов функции (F) с параметрами (x=1) и (y=6) |
| Результат работы программы |
Ответ: (10).
Решим задание из демоверсии (2023).
Алгоритм решения задания похож на предыдущий, исключением является то, что добавляется условие «траектория вычислений содержит число (10) и не содержит (17)». Нам нужно ввести ещё ограничение: «если (x) окажется больше (y), то команд получения из одного числа другого нет, т. е. (0)», и при появлении числа (17) тоже значение функции будет равно (0). Условие «содержит число (10)» запишем в строке вызова функции
(print(1,10)*(10,35))).
Программа
| 1 |
Объявим функцию (F), переменная (x) — первое число (из которого нужно начать работу), (y) — второе число, которое нужно получить |
|
1 2 |
Проверим условие: если (x) окажется больше (y), то команд получения из одного числа другого нет, т. е. (0). Также проверяем, если встречается (17), то возвращается (0) |
|
1 2 3 |
Проверим условие: если (x) равно (у), то команда есть, и она одна, поэтому возвращаем (1) команду |
|
1 2 3 4 |
Даная строка возвращает значение функции. Как видим, в записях «(x+1)», «(x*2)» заложены условия задания: 1) прибавь (1); |
|
1 2 3 4 5 |
Вызов функции (F) с параметрами. В данном задании вызов разбит на (2) части, так как условие — «включая (10)», поэтому запрашиваем два промежутка и перемножаем их |
| Вывод результата |
Ответ: (98).









 дискретным (прерывным). Состоит из последовательности простых шагов;
дискретным (прерывным). Состоит из последовательности простых шагов;