Задание 23. Преобразование логических выражений: демонстрационный вариант егэ информатика 2019; государственный выпускной экзамен 2019; тренировочные варианты ЕГЭ по информатике, тематические тестовые задания и задачи из тренажера по информатике 2019
Разбор 23 задания демоверсии егэ по информатике 2019:
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1 (y2 → (y3 ∧ x2)) ∧ (x2 → x3) = 1 … (y6 → (y7 ∧ x6)) ∧ (x6 → x7) = 1 y7 → x7 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x7, y1, y2, … y7, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
📹 Видеоразбор демоверсии егэ 2019
✍ Решение:
- Поскольку все равенства однотипны (кроме последнего), отличаются только сдвигом номеров переменных на единицу, то для решения будем использовать метод отображения: когда, найдя результат для первого равенства, необходимо применить тот же принцип с последующими равенствами, учитывая полученные результаты для каждого из них.
- Рассмотрим первое равенство. В нем внешняя операция — это конъюнкция, результат которой должна быть истина. Конъюнкция истинна если:
1 -> 1 т.е.: (y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1 1 1
(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 0
1 -> 0 = 0 т.е. случаи: y1=1 → (y2=0 ∧ x1=1) y1=1 → (y2=1 ∧ x1=0) y1=1 → (y2=0 ∧ x1=0)
(x1=1 → x2=0)
y7=1 → x7=0 = 0

1 + 7 + 28 = 36
Результат: 36
Статьи
Среднее общее образование
Информатика
Предлагаем вашему вниманию разбор задания №23 ЕГЭ 2019 года по информатике и ИКТ. Этот материал содержит пояснения и подробный алгоритм решения, а также рекомендации по использованию справочников и пособий, которые могут понадобиться при подготовке к ЕГЭ.
26 марта 2019

ЕГЭ-2020. Информатика. Тематические тренировочные задания
Пособие содержит задания, максимально приближенные к реальным, используемым на ЕГЭ, но распределенные по темам в порядке их изучения в 10-11-х классах старшей школы. Работая с книгой, можно последовательно отработать каждую тему, устранить пробелы в знаниях, а также систематизировать изучаемый материал. Такая структура книги поможет эффективнее подготовиться к ЕГЭ.
Купить
Демоверсия КИМ ЕГЭ-2019 по информатике не претерпела никаких изменений по своей структуре по сравнению с 2018 годом. Это значимо упрощает работу педагога и, конечно, уже выстроенный (хочется на это рассчитывать) план подготовки к экзамену обучающегося.
Мы рассмотрим решение предлагаемого проекта (на момент написания статьи – пока еще проекта) КИМ ЕГЭ по информатике.
Часть 1
Ответами к заданиям 1–23 являются число, последовательность букв или цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Задание 23
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(y1 → (y2 / x1)) / (x1 → x2) = 1
(y2 → (y3 / x2)) / (x2 → x3) = 1
…
(y6 → (y7 / x6)) / (x6 → x7) = 1
y7 → x7 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x7, y1, y2, … y7, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Ответ: ___________________________.
Решение
Довольно детальный разбор данной категории задач был опубликован в свое время в статье «Системы логических уравнений: решение с помощью битовых цепочек»3.
И для дальнейших рассуждений мы вспомним (для наглядности выпишем) некоторые определения и свойства:
|
[1] |
|
Определение импликации; |
|
|
[2] |
|
Распределительный закон 4; |
Посмотрим теперь на нашу систему еще раз. Обратим внимание, что ее можно переписать немного иначе. Для этого прежде всего заметим, что каждый из выделенных множителей в первых шести уравнениях, а также их взаимное произведение равны 1.
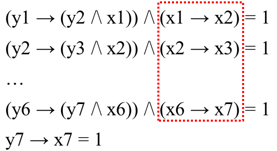
Т.е.

Немного поработаем над первыми множителями уравнений в системе:


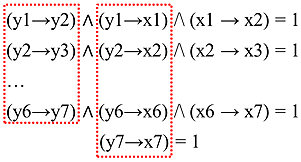
С учетом высказанных выше соображений, получим еще два уравнения, и исходная система уравнений примет вид:

В такой форме исходная система сводится к типовым заданиям, рассмотренным в указанной ранее статье.
Если рассмотреть отдельно первое и второе уравнения новой системы, то можно понять, что им соответствуют наборы:
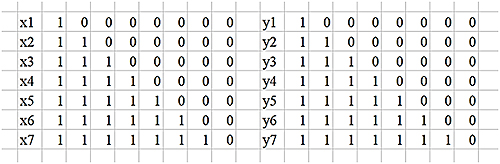
Эти рассуждения привели бы нас к возможным (8 × 8 = 64) вариантам решений, если бы не третье уравнение. В третьем уравнении мы сразу можем ограничиться рассмотрением только тех вариантов наборов, которые подходят для первых двух уравнений. Если подставить в третье уравнение первый набор y1…y7, состоящий только из 1, то очевидно, что ему будет соответствовать только один набор x1…x7, который также состоит только из 1. Любой другой набор, в котором есть хоть один 0, нам не подходит. Рассмотрим второй набор y1…y7 – 0111111. Для x1 допустимы оба возможных варианта значений – 0 и 1. Остальные значения, как и в предыдущем случае, не могут быть равны 0. Наборов, соответствующих данному условию, у нас два. Третьему набору y1…y7 – 011111 будут подходить первые три набора x1…x7. Рассуждая аналогично, мы получим, что искомое число наборов равно:
1 + 2 + … + 7 + 8 = 36.
Ответ: 36.
#ADVERTISING_INSERT#
Решение задания №23 Досрочный ЕГЭ по информатике 2019 от ФИПИ. Информатика ЕГЭ 23 задание разбор. Как решать задание №23 ЕГЭ по информатике 2019 г.
Сколько существует различных наборов значений логических переменных x1, x2, … x8, y1, y2, … y8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 / y1) ≡ (¬x2 / ¬y2)
(x2 / y2) ≡ (¬x3 / ¬y3)
…
(x7 / y7) ≡ (¬x8 / ¬y8)
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x8, y1, y2, … y8, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Здравствуйте! Сегодня речь пойдёт о 23 задании из ЕГЭ по информатике 2023.
Двадцать третье задание является последним заданием из первой части ЕГЭ по информатике 2023.
Давайте познакомимся с примерными задачами 23 задания из ЕГЭ по информатике 2023.
Задача (классическая)
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавить 3,
2. умножить на 2.
Первая из них увеличивает число на экране на 3, вторая — удваивает его.
Программа для Удвоителя — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 25 ?
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+3, y) + F(x*2, y) print(F(1, 25))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
Ответ получается равен 9.
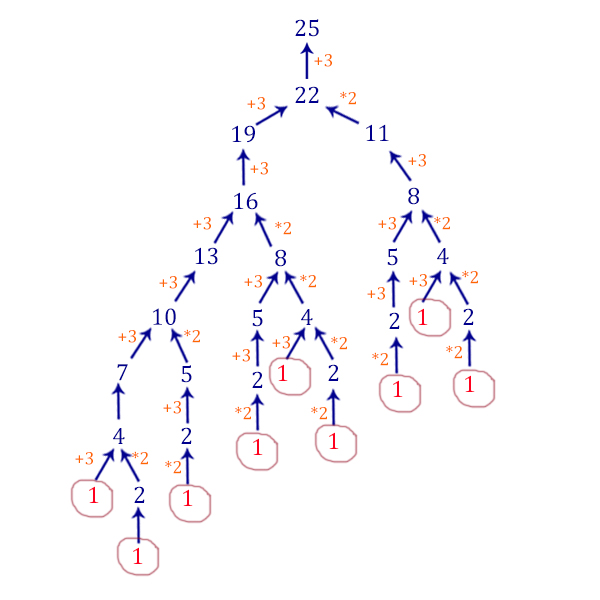
2 Способ (графический, для понимания)
Начинаем рассматривать задачку с конца. Если число нечётное, то оно может быть получено только с помощью первой команды. Если число чётное, то оно может быть получено с помощью двух команд.
Видим, что количество программ получается 9!
3 Способ (С помощью таблицы)
Некоторое число i можно получить только двумя способами: либо c помощью первой команды, либо с помощью второй команды. Тогда количество программ для некоторого числа i будет складываться из двух чисел: количества программ для числа i-3 и количества программ для числа i / 2 (Если i — чётное).
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| *2 | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 |
| Кол. Прог. |
1 | 1 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 3 |
| Числа | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| +3 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| *2 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | — |
| Кол. Прог. |
3 | 0 | 3 | 5 | 0 | 6 | 5 | 0 | 6 | 8 | 0 | 9 | 8 | 0 | 9 |
В первой строке пишутся числа от 1 до 25 (до того числа, которое нужно получить).
Во второй строке пишутся числа, которые в сумме с 3 (тройкой) дают числа, написанные в первой строке. (Прим. начиная с 4, числа идут по порядку.)
В третьей строке пишутся числа, которые при умножении на 2 дают числа, написанные в первой строке. (Прим. числа так же идут по порядку через одну пустую ячейку.)
В четвёртой строке для единицы ставим 1. Для остальных ячеек: смотрим, какие числа участвуют во второй и третьей строке для конкретной ячейки. Затем, эти числа ищем в первой строке и пишем сумму количеств программ для этих чисел (Т.е. пишем сумму уже известных значений из четвёртой строки для этих чисел).
Таким образом, основная идея 23 задания из ЕГЭ по информатике заключается в том, что результат каждого шага опирается на результаты предыдущих шагов!
Получаем ответ 9!
Ответ: 9
Задача (с избегаемым узлом)
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ — это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y or x==24: return 0 if x < y: return F(x+1, y) + F(x*2+1, y) print(F(1, 25))
Здесь на нельзя получать число 24, поэтому, если x будет равен 24, то мы возвращаем ноль.
Ответ получается равен 10.
2 способ (Решение с помощью таблицы).
Мы не может получать число 24! Значит, единственным способом добраться до числа 25 будет вторая команда.
Получается, что сначала нужно получить число 12, тогда 2 * 12 + 1 = 25 (2x+1). Это единственный путь!
Каждое число можем получить только 2 способами (Либо с помощью первой команды, либо с помощью второй команды). Поэтому количество программ для некоторого числа i будет равно сумме количеств команд для числа i-1 и для числа (i — 1) / 2 (Если число нечётное.) Если число i — чётное, то до числа i можно добраться единственным способом (с помощью первой команды).
Если записать с помощью массива:
A[i]=A[i-1] — если i — четное.
A[i]=A[i-1] + A[(i-1)/2] — если i нечетное;
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2x+1 | — | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол. Прог. |
1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 7 | 7 | 10 | 10 |
Ответ: 10
Задача (ЕГЭ по информатике, Москва, 2019)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает его на 2.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит число 9 и число 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(2, 9)*F(9, 11)*F(11, 12))
У нас числа 9 и 1 обязательные, поэтому разбиваем функцию следующим образом F(2, 9)*F(9, 11)*F(11, 12), через умножение. Это и будет ответ. Получается 50.
2 способ (с помощью таблицы).
От числа 11 до числа 12 можно добраться единственным путём (11 + 1 = 12).
От числа 9 до числа 11 можно добраться двумя способами (9 + 1 + 1 = 11, 9 + 2 = 11).
Найдём сколькими способами можно попасть от числа 2 до числа 9.
| Числа | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| +1 | — | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| *3 | — | — | — | — | 2 | — | — | 3 |
| +2 | — | — | 2 | 3 | 4 | 5 | 6 | 7 |
| Кол-во программ |
1 | 1 | 2 | 3 | 6 | 9 | 15 | 25 |
Учитывая, что от 9 до 11 двумя способами можно добраться, то 25 * 2 = 50 — это и будет ответ.
Ответ: 50
Задача ( ЕГЭ по информатике, Москва, 2020)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает на 2.
Сколько существует программ, которые преобразуют исходное число 3 в число 14 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(3, 9)*F(9, 14))
Ответ получается 112.
2 способ (с помощью таблицы).
Последней командой для получении любого числа из траектории программы может быть одна из трёх выше указанных команд!
Значит, количество программ для некоторого числа будет складываться из количества программ для тех чисел, из которых это число может быть получено.
Получается, что мы будем использовать основной принцип 23 задания из ЕГЭ по информатике: результат для некоторого числа опирается на результаты предыдущих чисел. Т.к. траектория вычислений программ обязательно должна проходить через число 9, то при вычислении результата для чисел больших 9, мы не можем опираться на результаты для чисел меньших 9 (Иначе мы пропустим число 9).
| Числа | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| +1 | — | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| *3 | — | — | — | — | — | — | 3 | — | — | — | — | — |
| +2 | — | — | 3 | 4 | 5 | 6 | 7 | — | 9 | 10 | 11 | 12 |
| Кол-во программ |
1 | 1 | 2 | 3 | 5 | 8 | 14 | 14 | 28 | 42 | 70 | 112 |
Ответ: 112
Посмотрим следующую задачу из 23 задания ЕГЭ по информатике 2023
Задача (с обязательным узлом, закрепление)
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x+3, y) print(F(1, 9)*F(9, 17))
Ответ получается 169.
2 способ (с помощью таблицы).
Любое число может получится в результате двух команд! Тогда количество программ для числа i будет складываться из количеств команд для числа i — 1 и для числа i — 3.
Если написать на языке массива
A[i] := A[i-1] + A[i-3], при i > 3.
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | — | — | 9 | 10 | 11 | 12 | 13 | 14 |
| Кол-во программ |
1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 13 | 13 | 26 | 39 | 52 | 78 | 117 | 169 |
При составлении значения для числа 10, мы не имеем право «заглядывать» за число 9, иначе число 9 будет пропущено! Поэтому для следующих трёх чисел (9, 9 + 1, 9 + 1 + 1), начиная с 9, будет 13 программ.
Для числа 17 получается ответ 169.
Ответ: 169
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Исполнитель А16 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает его на 2.
Программа для исполнителя А16 – это последовательность команд.
Сколько существует таких программ, которые исходное число 3 преобразуют в число 12 и при этом траектория вычислений программы содержит число 10?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 16, 18.
Источник: Демонстрационная версия ЕГЭ—2017 по информатике.
2
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203
3
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10204
4
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 4.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 4.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10103
5
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 3.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104
Пройти тестирование по этим заданиям
Автор материалов — Лада Борисовна Есакова.
Решение систем логических уравнений методом замены переменных
Метод замены переменных применяется, если некоторые переменные входят в состав уравнений только в виде конкретного выражения, и никак иначе. Тогда это выражение можно обозначить новой переменной.
Пример 1.
Сколько существует различных наборов значений логических переменных x1, х2, х3, х4, х5, х6, х7, х8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → х2) → (х3→ х4) = 1
(х3 → х4) → (х5 → х6) = 1
(х5 → х6) → (х7 → х8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, х6, х7, х8, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение:
Сделаем замену переменных:
(x1 → х2) = y1; (х3 → х4) = y2; (х5 → х6) = y3; (х7 → х8) = y4.
Тогда можно записать систему в виде одного уравнения:
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1. Конъюнкция равна 1 (истинна), когда каждый операнд принимает значение 1. Т.е. каждая из импликаций должна быть истинна, а это выполняется при всех значениях, кроме (1 → 0). Т.е. в таблице значений переменных y1, y2, y3, y4 единица не должна стоять левее нуля:
|
y1 |
y2 |
y3 |
y4 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
Т.е. условия выполняются для 5 наборов y1-y4.
Т.к. y1 = x1 → x2, то значение y1 = 0 достигается на единственном наборе x1, x2: (1, 0), а значение y1 = 1 – на трех наборах x1, x2: (0,0) , (0,1), (1,1). Аналогично для y2, y3, y4.
Поскольку каждый набор (x1,x2) для переменной y1 сочетается с каждым набором (x3,x4) для переменной y2 и т.д., то количества наборов переменных x перемножаются:
|
y1 |
y2 |
y3 |
y4 |
Кол-во наборов на x1…x8 |
|
0 |
0 |
0 |
0 |
1*1*1*1 = 1 |
|
0 |
0 |
0 |
1 |
1*1*1*3 = 3 |
|
0 |
0 |
1 |
1 |
1*1*3*3 = 9 |
|
0 |
1 |
1 |
1 |
1*3*3*3 = 27 |
|
1 |
1 |
1 |
1 |
3*3*3*3 = 81 |
Сложим количество наборов: 1 + 3 + 9 + 27 + 81 = 121.
Ответ: 121
Пример 2.
Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?
(¬ (x1 ≡ y1)) ≡ (x2 ≡ y2)
(¬ (x2 ≡ y2)) ≡ (x3 ≡ y3)
…
(¬ (x8 ≡ y8)) ≡ (x9 ≡ y9)
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x9, y1, y2, … y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение:
Сделаем замену переменных:
(x1 ≡ y1) = z1, (x2 ≡ y2) = z2,…. ,(x9 ≡ y9) = z9
Систему можно записать в виде одного уравнения:
(¬ z1 ≡ z2) ∧ (¬ z2 ≡ z3) ∧ …..∧ (¬ z8 ≡ z9)
Эквивалентность истинна, только если оба операнда равны. Решениями этого уравнения будут два набора:
| z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Т.к. zi = (xi ≡ yi), то значению zi = 0 соответствуют два набора (xi,yi): (0,1) и (1,0), а значению zi = 1 — два набора (xi,yi): (0,0) и (1,1).
Тогда первому набору z1, z2,…, z9 соответствует 29 наборов (x1,y1), (x2,y2),…, (x9,y9).
Столько же соответствует второму набору z1, z2,…, z9. Тогда всего 29 +29 = 1024 наборов.
Ответ:1024
Решение систем логических уравнений методом визуального определения рекурсии.
Этот метод применяется, если система уравнений достаточно проста и порядок увеличения количества наборов при добавлении переменных очевиден.
Пример 3.
Сколько различных решений имеет система уравнений
¬x1 ∨ x2 = 1
¬x2 ∨ x3 = 1
…
¬x9 ∨ x10 = 1,
где x1, x2, … x10 — логические переменные?
В ответе не нужно перечислять все различные наборы значений x1, x2, … x10, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение:
Решим первое уравнение. Дизъюнкция равна 1, если хотя бы один из ее операндов равен 1. Т.е. решениями являются наборы:
Для x1=0 существуют два значения x2 ( 0 и 1), а для x1=1 только одно значение x2 (1), такие, что набор (x1,x2) является решением уравнения. Всего 3 набора.
Добавим переменную x3 и рассмотрим второе уравнение. Оно аналогично первому, значит для x2=0 существуют два значения x3 ( 0 и 1), а для x2=1 только одно значение x3 (1), такие, что набор (x2,x3) является решением уравнения. Всего 4 набора.
Несложно заметить, что при добавлении очередной переменной добавляется один набор. Т.е. рекурсивная формула количества наборов на (i+1) переменных:
Ni+1 = Ni + 1. Тогда для десяти переменных получим 11 наборов.
Ответ: 11
Решение систем логических уравнений различного типа
Пример 4.
Сколько существует различных наборов значений логических переменных x1, …, x4, y1,…, y4, z1,…, z4, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1
(z1 → z2) ∧ (z2→ z3) ∧ (z3 → z4) = 1
x4 ∧ y4 ∧ z4 = 0
В ответе не нужно перечислять все различные наборы значений переменных x1, …, x4, y1, …, y4, z1, …, z4, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Решение:
Заметим, что три уравнения системы одинаковы на различных независимых наборах переменных.
Рассмотрим первое уравнение. Конъюнкция истинна (равна 1) только тогда, когда все ее операнды истинны (равны 1). Импликация равна 1 на всех наборах, кроме (1,0). Значит, решением первого уравнения будут такие наборы x1, x2, x3, x4, в которых 1 не стоит левее 0 (5 наборов):
|
x1 |
x2 |
x3 |
x4 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
Аналогично, решениями второго и третьего уравнений будут абсолютно такие же наборы y1,…,y4 и z1,…, z4.
Теперь проанализируем четвертое уравнение системы: x4 ∧ y4 ∧ z4 = 0. Решением будут все наборы x4, y4, z4, в которых хотя бы одна из переменных равна 0.
Т.е. для x4 = 0 подойдут все возможные наборы (y4, z4), а для x4 = 1 подойдут наборы (y4, z4), в которых присутствует хотя бы один ноль : (0, 0), (0,1) , (1,0).
|
x1 |
x2 |
x3 |
x4 |
Кол-во наборов (y4, z4) |
|
0 |
0 |
0 |
0 |
5*5 = 25 |
|
0 |
0 |
0 |
1 |
1 + 4 + 4 = 9 |
|
0 |
0 |
1 |
1 |
1 + 4 + 4 = 9 |
|
0 |
1 |
1 |
1 |
1 + 4 + 4 = 9 |
|
1 |
1 |
1 |
1 |
1 + 4 + 4 = 9 |
Общее количество наборов 25 + 4*9 = 25 + 36 = 61.
Ответ: 61
Решение систем логических уравнений методом построения рекуррентных формул
Метод построения рекуррентных формул применяется при решении сложных систем, в которых порядок увеличения количества наборов неочевиден, а построение дерева невозможно из-за объемов.
Пример 5.
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(x1 ∨ y1) ∧ ((x2 ∧ y2) → (x1 ∧ y1)) = 1
(x2 ∨ y2) ∧ ((x3 ∧ y3) → (x2 ∧ y2)) = 1
…
(x6 ∨ y6) ∧ ((x7 ∧ y7) → (x6 ∧ y6)) = 1
(x7 ∨ y7) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, …, x7, y1, y2, …, y7, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение:
Заметим, что первые шесть уравнений системы одинаковы и отличаются только набором переменных. Рассмотрим первое уравнение. Его решением будут следующие наборы переменных:
Обозначим:
число наборов (0,0) на переменных (x1,y1) через A1,
число наборов (0,1) на переменных (x1,y1) через B1,
число наборов (1,0) на переменных (x1,y1) через C1,
число наборов (1,1) на переменных (x1,y1) через D1.
число наборов (0,0) на переменных (x2,y2) через A2,
число наборов (0,1) на переменных (x2,y2) через B2,
число наборов (1,0) на переменных (x2,y2) через C2,
число наборов (1,1) на переменных (x2,y2) через D2.
Из дерева решений видим, что
A1=0, B1=1, C1=1, D1=1.
Заметим, что набор (0,0) на переменных (x2,y2) получается из наборов (0,1), (1,0) и (1,1) на переменных (x1,y1). Т.е. A2=B1+C1+D1.
Набор (0,1) на переменных (x2,y2) получается из наборов (0,1), (1,0) и (1,1) на переменных (x1,y1). Т.е. B2=B1+C1+D1.
Аналогично рассуждая, заметим, что С2=B1+C1+D1. D2= D1.
Таким образом, получаем рекуррентные формулы:
Ai+1 = Bi + Ci + Di
Bi+1 = Bi + Ci + Di
Ci+1 = Bi + Ci + Di
Di+1 = Ai +Bi + Ci + Di
Составим таблицу
| Наборы | Обозн. | Формула |
Количество наборов |
||||||
| i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | i=7 | |||
| (0,0) | Ai | Ai+1=Bi+Ci+Di | 0 | 3 | 7 | 15 | 31 | 63 | 127 |
| (0,1) | Bi | Bi+1=Bi+Ci+Di | 1 | 3 | 7 | 15 | 31 | 63 | 127 |
| (1,0) | Ci | Ci+1=Bi+Ci+Di | 1 | 3 | 7 | 15 | 31 | 63 | 127 |
| (1,1) | Di | Di+1=Di | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Последнему уравнению (x7 ∨ y7) = 1 удовлетворяют все наборы, кроме тех, в которых x7=0 и y7=0. В нашей таблице число таких наборов A7.
Тогда общее количество наборов равно B7 + C7 + D7 = 127+127+1 = 255
Ответ: 255
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №23. Решение систем логических уравнений.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.03.2023
Решение задания ЕГЭ-23 методом отображений
Задание 23 из демоверсии 2019 года
Поскольку все равенства однотипны (кроме последнего), отличаются только сдвигом номеров переменных на единицу, то для решения будем использовать метод отображения.
Рассмотрим первое уравнение:
Внешняя операция конъюнкция. Значение выражения равно 1, если оба множителя равны 1.
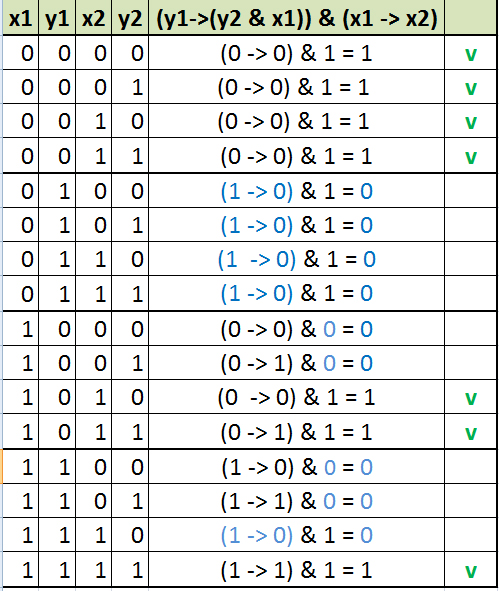
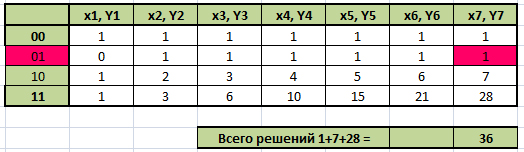
Составим таблицу истинности для первого уравнения и отметим строки, в которых значение выражения истинно.
Переменных 4 (x1, y1, x2, y2). Количество строк в таблице истинности — 16.
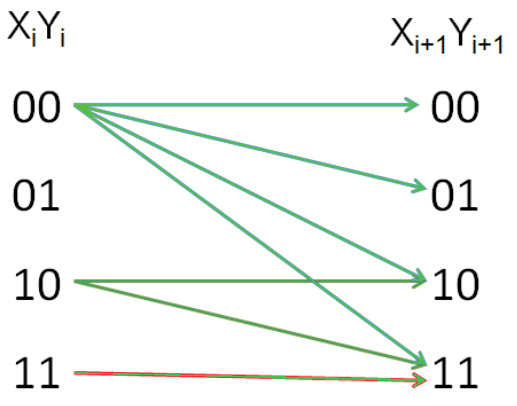
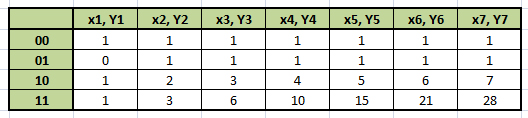
Составим схему отображения:
Найдём общее количество решений:
Вернёмся к последнему равенству: y7 -> x7 =1.
Исключим случаи, когда y7 -> x7 =0, то есть y7=1, а x7=0.
Ответ: 36.