Решение и ответы заданий Варианта №5 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения sqrt{9-8x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание 2.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.
Задание 3.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Задание 4.
Найдите значение выражения frac{2^{log_{9}3}}{2^{log_{9}243}}.
Задание 5.
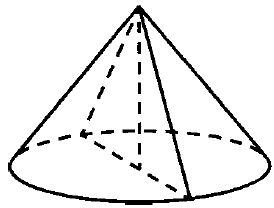
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
Задание 6.
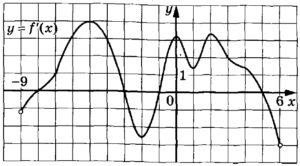
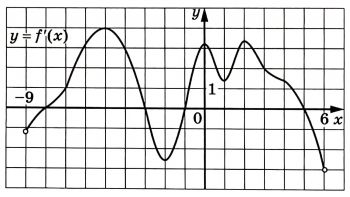
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Задание 7.
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v0 = 1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с2. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Задание 8.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
Задание 9.
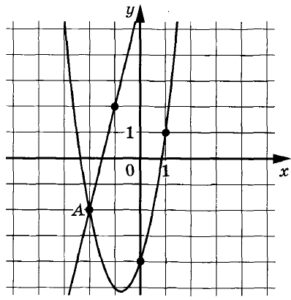
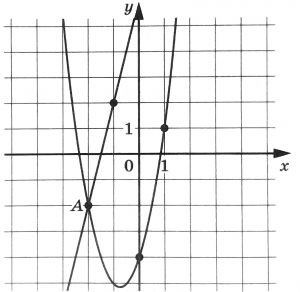
На рисунке изображены функций графики f(x) = ах2 + bх + с и g(x) = kx + d, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Задание 10.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите наибольшее значение функции у = х5 + 5х3 – 140х на отрезке [–8; –1].
Задание 12.
а) Решите уравнение sin2x + cos2x = 1.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; –2pi].
Задание 13.
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l.
а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми l и СВ1.
Задание 14.
Решите неравенство 7^{log_{frac{1}{7}}log_{frac{1}{2}}(-x)}< 2^{log_{frac{1}{2}}log_{frac{1}{7}}(-x)}.
Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
– в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
– в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{12}{49} площади трапеции ABCD.
Задание 17.
Найдите все такие значения а, при каждом из которых неравенство
–1 ≤ sinx(a – cos2x) ≤ 1
верно при всех действительных значениях х.
Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 8
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 1
Решите уравнение $$sqrt{9-8x}=-x$$. Если уравнение имеет более одного корня, запишите больший из корней.
Ответ: -9
Скрыть
В видео в самом конце выбор корня с косяком, выбираем -9, а не 1.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, 61,99 мм, чем или больше, чем 62,01 мм.
Ответ: 0,014
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
Биссектриса тупого утла параллелограмма делит противоположную сторону в отношении 3 :4 , считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Ответ: 11,55
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Найдите значение выражения: $$frac{2^{log_{9}3}}{2^{log_{9}243}}$$
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
Ответ: 432
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
На рисунке изображён график y=f’(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(х). В ответе укажите длину наибольшего из них.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону $$v=v_{0}cos frac{2pi t}{T}$$, где t — время с момента начала колебаний, Т=2 с — период колебаний, v0=1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле $$E=frac{mv^{2}}{2}$$, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Ответ: 0,32
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
На рисунке изображены графики функций $$f(x)=ax^{2}+bx+c$$ и $$g(x)=kx+d$$, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ: 2,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Ответ: 0,06
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11
Найдите наибольшее значение функции $$y=x^{5}+5x^{3}-140x$$ на отрезке [-8;-1].
Ответ: 208
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
а) Решите уравнение: $$sin 2x+cos 2x=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi}{2};-2pi]$$
Ответ: а)$$pi k; frac{pi}{4}+pi n,n,kin Z$$ б)$$-3pi; -frac{11pi}{4};-2pi$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
В правильной призме ABCDA1B1C1D1с основанием ABCD боковое ребро равно $$sqrt{3}$$, а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1проведена прямая I.
а) Докажите, что прямая I пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми I и СВ1.
Ответ: $$arccos frac{2sqrt{210}}{35}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
Решите неравенство: $$7^{log_{frac{1}{7}}log_{frac{1}{2}}(-x)}<2^{log_{frac{1}{2}}log_{frac{1}{7}}(-x)}$$
Ответ: $$(-1;0)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на г % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть , долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите г.
Ответ: 16
Скрыть
В видео в самом конце поделил 48 на 3 неверно, конечно, там получится 16, а не 3.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что $$angle AOB=angle COD=90^{circ}$$.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ=CD, а площадь четырёхугольника с вершинами в точках касания 12 окружности со сторонами трапеции составляет $$frac{12}{49}$$ площади трапеции ABCD.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 17
Найдите все такие значения а, при каждом из которых неравенство $$-1leq |sin x(a-cos 2x)|leq 1$$ верно при всех действительных значениях х.
Ответ: $$[1-1,5sqrt[3]{4};0]$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Ответ: а)да б)нет в)26
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

| 3135 | При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм |
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 2 | |
| 3134 | Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33 |
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 3 | |
| 3133 | На рисунке изображен график y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них |
Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 6 | |
| 3131 | Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч |
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 8 | |
| 3130 | Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых |
Биатлонист 4 раза стреляет по мишеням ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 10 | |
| 3129 | Найдите наибольшее значение функции y=x^5+5x^3-140x на отрезке [-8; -1] |
Найдите наибольшее значение функции y=x5 + 5×3 — 140x ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 11 | |
| 3128 | а) Решите уравнение sin(2x)+cos(2x)=1 б) Найдите все корни этого уравнения, принадлежащие отрезку [-(7pi)/2; -2pi]. |
а) Решите уравнение sin2x + cos2x = 1 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 12 | |
| 3127 | В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно sqrt3, а сторона основания равна 2. Через точку A1 перпендикулярно плоскости AB1D1 проведена прямая l. а) Докажите, что прямая l пересекает отрезок AC и делит его в отношении 3:1. б) Найдите угол между прямыми l и CB1 |
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно корень из 3, а сторона основания равна 2 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 13 | |
| 3126 | Около окружности с центром O описана трапеция ABCD с основаниями AD и BC. а) Докажите, что /_AOB = /_COD=90^@ б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет 12/49 площади трапеции ABCD |
б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB = CD ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 16 | |
| 3125 | Решите неравенство 7^(log_{1/7}(log_{1/2}(-x))) < 2^(log_{1/2}(log_{1/7}(-x))) |
Решите неравенство 7 log 1/7 log 1/2 (-x) < 2 log 1/2 log 1/7 (-x) ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 14 | |
| Clear |
Канал видеоролика: Виктор Осипов
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #егэпоматематике #ответы_егэ #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

ОГЭ 2022 Ященко 1 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 2 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 3 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 4 вариант ФИПИ школе полный разбор!
Виктор Осипов
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
26.11.2021
Решений пока нет, можете прикрепить свои на форум. Копка добавления появится после завершения теста. Или откройте нужную задачу отдельно дальше в главе.
Решите уравнение (sqrt{9-8x}=-x). Если уравнение имеет более одного корня, в ответе запишите больший из корней.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Найдите значение выражения (dfrac{2^{log_93}}{2^{log_9243}})
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Груз массой 0,25 кг колеблется на пружине. Его скорость (v) меняется по закону (v = v_0 cosdfrac{2pi t}{T}), где (t) – время с момента начала колебаний, (T= 2) с – период колебаний, (v_0= 1{,}6) м/с. Кинетическая энергия (E) (в джоулях) груза вычисляется по формуле (E = dfrac{mv^2}{2}), где (m) – масса груза в килограммах, (v) – скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
На рисунке изображены графики функций (f(x)=ax^2+bx+c) и (g(x)=kx+d), которые пересекаются в точках А и В. Найдите абсциссу точки В.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Найдите наибольшее значение функции ( y=x^5+5x^3-140x ) на отрезке (left[-8;-1right])
а) Решите уравнение (sin{2x}+cos{2x}=1).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{7pi}{2};-2piright] ).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно (sqrt{3}) , а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая (l).
а) Докажите, что прямая (l) пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми (l) и СВ1.
Решите неравенство ( 7^{log_{frac{1}{7}}{log_{frac{1}{2}}{left(-xright)}}}< 2^{log_{frac{1}{2}}{log_{frac{1}{7}}{left(-xright)}}} )
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на 20% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Около окружности с центром (O) описана трапеция (ABCD) с основаниями (AD) и (BC).
а) Докажите, что (angle AOB = angle COD = 90^{circ}).
б) Найдите отношение большего основания трапеции к меньшему, если известно, что (AB = CD), а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет (dfrac{12}{49}) площади трапеции (ABCD).
Найдите все такие значения (a), при каждом из которых неравенство (-1leqslantsin x(a-cos2x)leqslant1) верно при всех действительных значениях (x).
Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Решение и ответы заданий Варианта №5 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения sqrt{9-8x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание 2.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.
Задание 3.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Задание 4.
Найдите значение выражения frac{2^{log_{9}3}}{2^{log_{9}243}}.
Задание 5.
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
Задание 6.
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Задание 7.
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v0 = 1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с2. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Задание 8.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
Задание 9.
На рисунке изображены функций графики f(x) = ах2 + bх + с и g(x) = kx + d, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Задание 10.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите наибольшее значение функции у = х5 + 5х3 – 140х на отрезке [–8; –1].
Задание 12.
а) Решите уравнение sin2x + cos2x = 1.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; –2pi].
Задание 13.
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l.
а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми l и СВ1.
Задание 14.
Решите неравенство 7^{log_{frac{1}{7}}log_{frac{1}{2}}(-x)}< 2^{log_{frac{1}{2}}log_{frac{1}{7}}(-x)}.
Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
– в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
– в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.
Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{12}{49} площади трапеции ABCD.
Задание 17.
Найдите все такие значения а, при каждом из которых неравенство
–1 ≤ sinx(a – cos2x) ≤ 1
верно при всех действительных значениях х.
Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 8
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 1
Решите уравнение $$sqrt{9-8x}=-x$$. Если уравнение имеет более одного корня, запишите больший из корней.
Ответ: -9
Скрыть
В видео в самом конце выбор корня с косяком, выбираем -9, а не 1.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, 61,99 мм, чем или больше, чем 62,01 мм.
Ответ: 0,014
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3
Биссектриса тупого утла параллелограмма делит противоположную сторону в отношении 3 :4 , считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.
Ответ: 11,55
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 4
Найдите значение выражения: $$frac{2^{log_{9}3}}{2^{log_{9}243}}$$
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 5
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.
Ответ: 432
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 6
На рисунке изображён график y=f’(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(х). В ответе укажите длину наибольшего из них.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 7
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону $$v=v_{0}cos frac{2pi t}{T}$$, где t — время с момента начала колебаний, Т=2 с — период колебаний, v0=1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле $$E=frac{mv^{2}}{2}$$, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.
Ответ: 0,32
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 8
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 9
На рисунке изображены графики функций $$f(x)=ax^{2}+bx+c$$ и $$g(x)=kx+d$$, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ: 2,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 10
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Ответ: 0,06
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 11
Найдите наибольшее значение функции $$y=x^{5}+5x^{3}-140x$$ на отрезке [-8;-1].
Ответ: 208
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 12
а) Решите уравнение: $$sin 2x+cos 2x=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi}{2};-2pi]$$
Ответ: а)$$pi k; frac{pi}{4}+pi n,n,kin Z$$ б)$$-3pi; -frac{11pi}{4};-2pi$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 13
В правильной призме ABCDA1B1C1D1с основанием ABCD боковое ребро равно $$sqrt{3}$$, а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1проведена прямая I.
а) Докажите, что прямая I пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми I и СВ1.
Ответ: $$arccos frac{2sqrt{210}}{35}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
Решите неравенство: $$7^{log_{frac{1}{7}}log_{frac{1}{2}}(-x)}<2^{log_{frac{1}{2}}log_{frac{1}{7}}(-x)}$$
Ответ: $$(-1;0)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на г % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть , долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите г.
Ответ: 16
Скрыть
В видео в самом конце поделил 48 на 3 неверно, конечно, там получится 16, а не 3.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 16
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что $$angle AOB=angle COD=90^{circ}$$.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ=CD, а площадь четырёхугольника с вершинами в точках касания 12 окружности со сторонами трапеции составляет $$frac{12}{49}$$ площади трапеции ABCD.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Найдите все такие значения а, при каждом из которых неравенство $$-1leq |sin x(a-cos 2x)|leq 1$$ верно при всех действительных значениях х.
Ответ: $$[1-1,5sqrt[3]{4};0]$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Ответ: а)да б)нет в)26
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
| 3135 | При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм |
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 2 | |
| 3134 | Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33 |
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 3 | |
| 3133 | На рисунке изображен график y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них |
Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 6 | |
| 3131 | Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч |
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 8 | |
| 3130 | Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых |
Биатлонист 4 раза стреляет по мишеням ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 10 | |
| 3129 | Найдите наибольшее значение функции y=x^5+5x^3-140x на отрезке [-8; -1] |
Найдите наибольшее значение функции y=x5 + 5×3 — 140x ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 11 | |
| 3128 | а) Решите уравнение sin(2x)+cos(2x)=1 б) Найдите все корни этого уравнения, принадлежащие отрезку [-(7pi)/2; -2pi]. |
а) Решите уравнение sin2x + cos2x = 1 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 12 | |
| 3127 | В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно sqrt3, а сторона основания равна 2. Через точку A1 перпендикулярно плоскости AB1D1 проведена прямая l. а) Докажите, что прямая l пересекает отрезок AC и делит его в отношении 3:1. б) Найдите угол между прямыми l и CB1 |
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно корень из 3, а сторона основания равна 2 ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 13 | |
| 3126 | Около окружности с центром O описана трапеция ABCD с основаниями AD и BC. а) Докажите, что /_AOB = /_COD=90^@ б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет 12/49 площади трапеции ABCD |
б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB = CD ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 16 | |
| 3125 | Решите неравенство 7^(log_{1/7}(log_{1/2}(-x))) < 2^(log_{1/2}(log_{1/7}(-x))) |
Решите неравенство 7 log 1/7 log 1/2 (-x) < 2 log 1/2 log 1/7 (-x) ! 36 вариантов ФИПИ Ященко 2022 Вариант 5 Задание 14 | |
| Clear |
Канал видеоролика: Виктор Осипов
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #егэпоматематике #ответы_егэ #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

ОГЭ 2022 Ященко 1 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 2 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 3 вариант ФИПИ школе полный разбор!
Виктор Осипов

ОГЭ 2022 Ященко 4 вариант ФИПИ школе полный разбор!
Виктор Осипов
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
Дата публикации:
26.12.2021 12:06
Продолжительность:
46:28
Ссылка:
https://thewikihow.com/video_C5LCsgZK8EY
Действия:
Источник:
Описание
Подписывайтесь на наш Telegram канал!@thewikihowоткрытьМониторим видео тренды 24/7
Что еще посмотреть на канале Инженер-Математик
Фото обложки и кадры из видео
Егэ 2022 Математика Профиль. Ященко Вариант 5. Полный Разбор, Инженер-Математик
https://thewikihow.com/video_C5LCsgZK8EY
Аналитика просмотров видео на канале Инженер-Математик
Гистограмма просмотров видео «Егэ 2022 Математика Профиль. Ященко Вариант 5. Полный Разбор» в сравнении с последними загруженными видео.
Теги:
Егэ 2022 Математика Профиль
Ященко Егэ
Фипи Школе
Вариант 5
Ященко Вариант 5
Похожие видео
01:14:01
26 497 просмотров.
45:29
3 001 просмотр.
01:05:00
33 533 просмотра.
01:19:29
106 281 просмотр.
09:34
917 просмотров.
46:17
1 200 просмотров.
01:19:39
295 109 просмотров.
02:52:56
20 972 просмотра.
01:24:44
78 529 просмотров.
Поделиться
Смотрите также
- ©2006 ‐ 2023 iBlogger.Ru
- Правообладателям
- О сайте
Смотрите также
-
- © 2014 — 2023 «Game 🏃 Runs» — прохождения видеоигр
- Отказ от ответственности
- Правообладателям
- Постеры игр: © MobyGames.com
- Полезное