Решение 9 задания егэ математика профильный уровень 2022 парабола

Каталог заданий.
Параболы


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 10 № 509253

На рисунке изображены графики функций f левая круглая скобка x правая круглая скобка =4x в квадрате минус 25x плюс 41 и g левая круглая скобка x правая круглая скобка =ax в квадрате плюс bx плюс c, которые пересекаются в точках A и B. Найдите абсциссу точки B.

Аналоги к заданию № 509253: 509254 509255 509259 509262 509263 509264 509268 509256 509257 509258 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

2

Тип 10 № 562060

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 3,5 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

3

Тип 10 № 562061

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение дискриминанта уравнения f левая круглая скобка x правая круглая скобка =0.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

1 комментарий · Сообщить об ошибке · Помощь

4

Тип 10 № 562153

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 13 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

5

Тип 10 № 562154

На рисунке изображён график функции вида f левая круглая скобка x правая круглая скобка = дробь: числитель: x в квадрате , знаменатель: a конец дроби плюс bx плюс c, где числа a, b и c  — целые. Найдите значение f левая круглая скобка 10 правая круглая скобка .

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

·

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике. 

Способы решения номера

9 задание по математике профильного уровня 2022 получится решить четырьмя методами. 

Первый вариант

Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом: 

Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки: 

Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты: 

16a — 4b + c = -3

Аналогичным образом записываем выражение, используя две остальные точки: 

9a — 3b + c = -2

4a — 2b + c = 1

Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем: 

b = 8;

c = 13. 

Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы: 

f(x) = x2 + 8x + 13

f(-12) = 144 — 96 + 13 = 61

Второй вариант

Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы: 

Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще. 

Третий вариант

9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример: 

y = x2

Сдвиг влево записывается: 

y = (x + 4)2

Сдвиг вниз: 

y = (x + 4)2 — 3

Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61. 

Четвертый вариант

Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат: 

Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!

В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum. 

Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации! 

Источник
Skip to content

ЕГЭ Профиль №9. Парабола

ЕГЭ Профиль №9. Параболаadmin2022-08-17T22:38:16+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Парабола

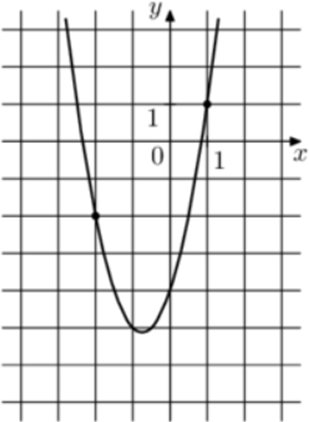
Задача 1. На рисунке изображён график функции  (fleft( x right) = 2{x^2} + b,x + c.)  Найдите  (fleft( { — 5} right).)

Ответ

ОТВЕТ: 31.
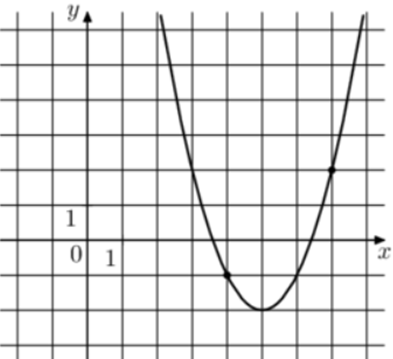
Задача 2. На рисунке изображён график функции  (fleft( x right) = {x^2} + b,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: 34.
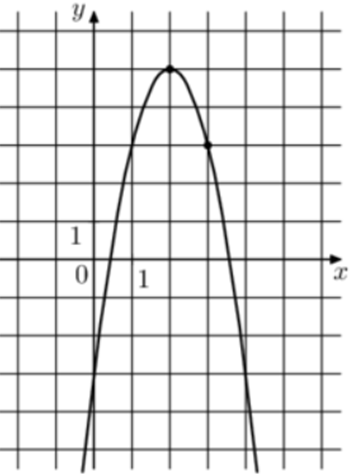
Задача 3. На рисунке изображён график функции  (fleft( x right) =  — 2{x^2} + b,x + c.)  Найдите  (fleft( 6 right).)

Ответ

ОТВЕТ: — 27.
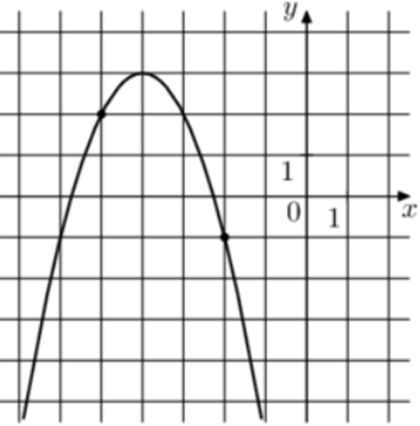
Задача 4. На рисунке изображён график функции  (fleft( x right) =  — {x^2} + b,x + c.)  Найдите  (fleft( { — 8} right).)

Ответ

ОТВЕТ: — 13.
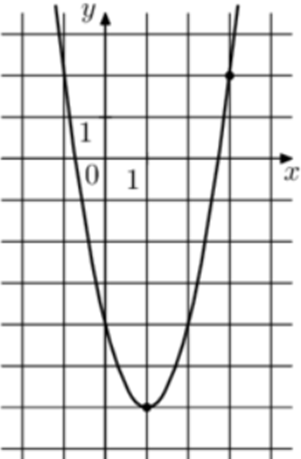
Задача 5. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 4,x + c.)  Найдите  (fleft( { — 3} right).)

Ответ

ОТВЕТ: 26.
Задача 6. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 7,x + c.)  Найдите  (fleft( 7 right).)

Ответ

ОТВЕТ: 47.
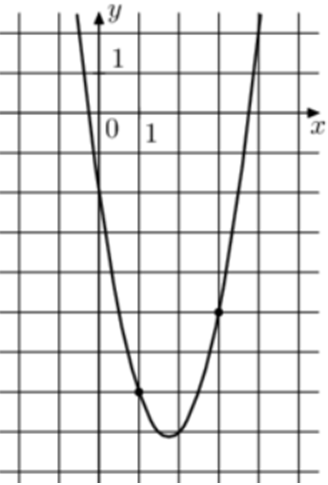Задача 7. На рисунке изображён график функции  (fleft( x right) = a,{x^2} — 3,x + c.)  Найдите  (fleft( { — 4} right).)

Ответ

ОТВЕТ: — 14.
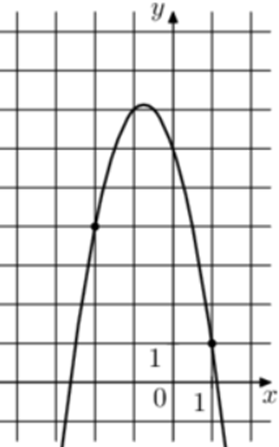Задача 8. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + 10,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: — 33.
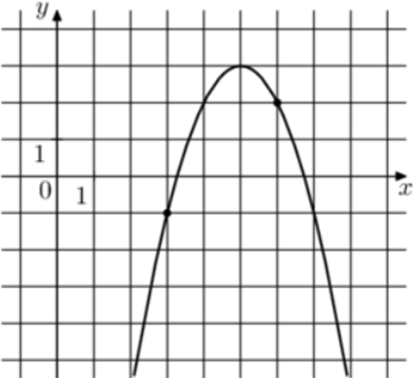Задача 9. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 6.)  Найдите  (fleft( { — 6} right).)

Ответ

ОТВЕТ: 48.
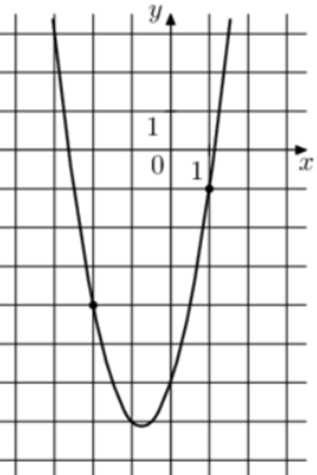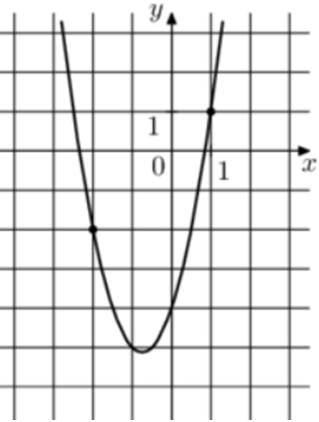
Задача 10. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 4.)  Найдите  (fleft( { — 4} right).)

Ответ

ОТВЕТ: 16.
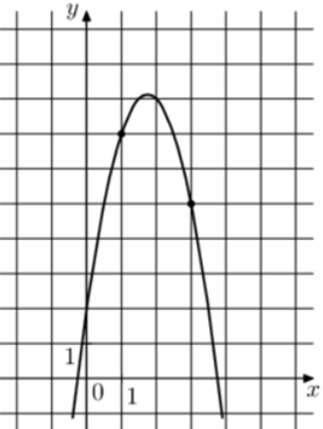
Задача 11. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + 2.)  Найдите  (fleft( { — 3} right).)

Ответ

ОТВЕТ: — 37.
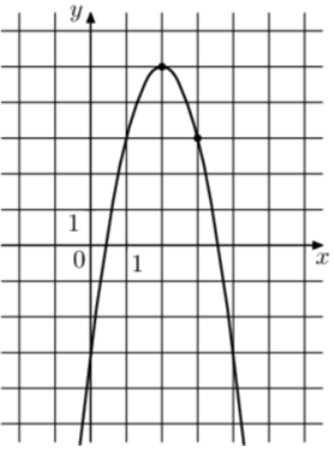
Задача 12. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x — 3.)  Найдите  (fleft( 8 right).)

Ответ

ОТВЕТ: — 67.
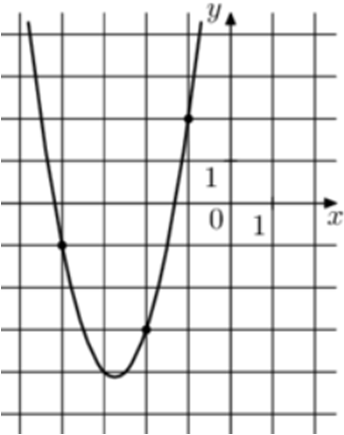
Задача 13. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( { — 7} right).)

Ответ

ОТВЕТ: 32.
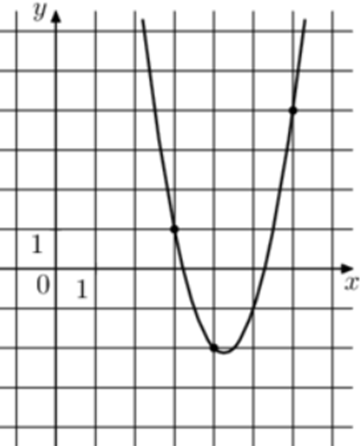
Задача 14. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( {10} right).)

Ответ

ОТВЕТ: 64.
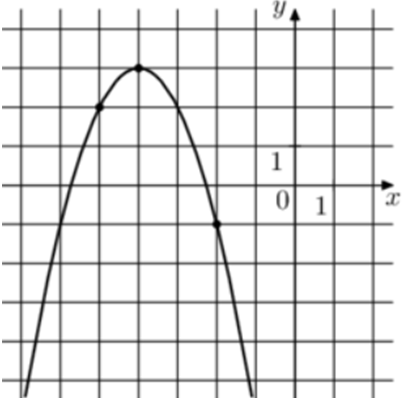
Задача 15. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( 2 right).)

Ответ

ОТВЕТ: — 33.
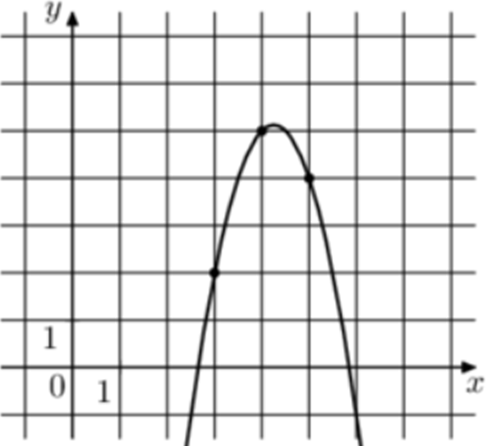
Задача 16. На рисунке изображён график функции  (fleft( x right) = a,{x^2} + b,x + c.)  Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: — 50.
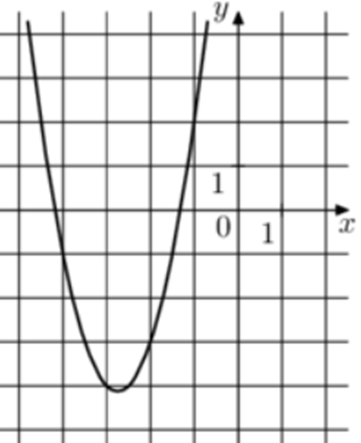
Задача 17. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( 2 right).)

Ответ

ОТВЕТ: 41.
Задача 18. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 1} right).)

Ответ

ОТВЕТ: 34.
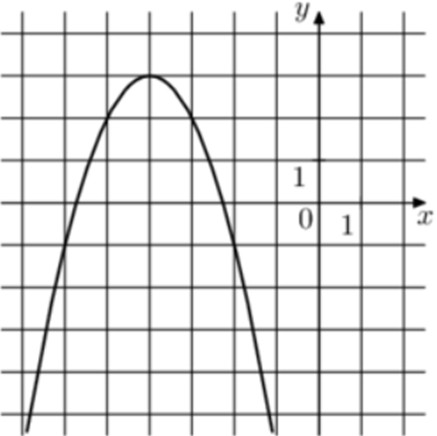
Задача 19. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 8} right).)

Ответ

ОТВЕТ: — 13.
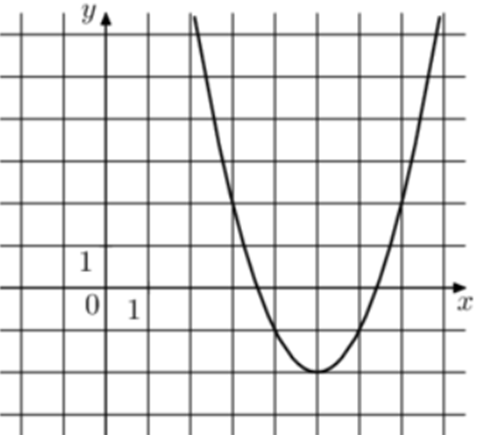
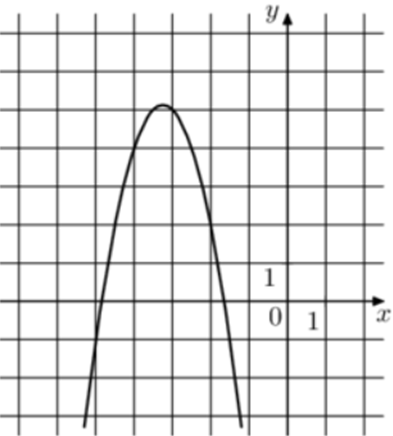
Задача 20. На рисунке изображены графики функций  (fleft( x right) = a,{x^2} + b,x + c,)  где a, b и c – целые. Найдите  (fleft( { — 6} right).)

Ответ

ОТВЕТ: — 10.
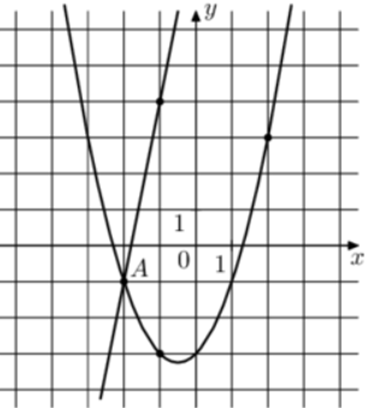
Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 6.
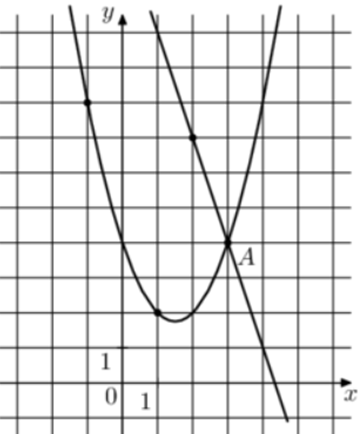
Задача 22. На рисунке изображены графики функций (fleft( x right) =  — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 3.
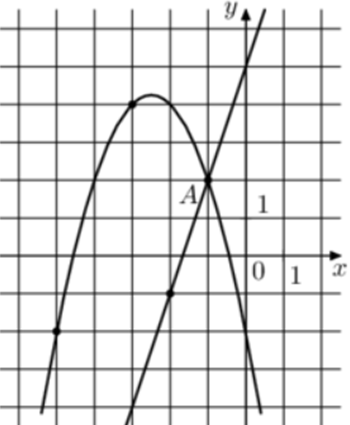
Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 7.
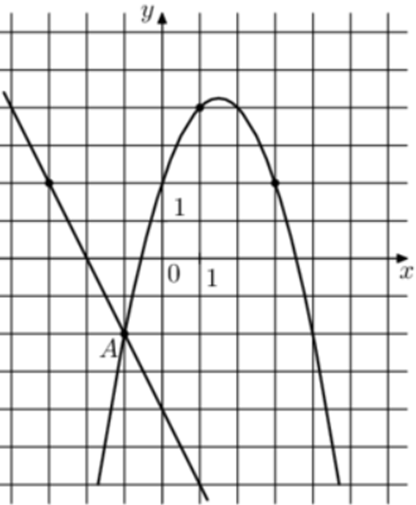
Задача 24. На рисунке изображены графики функций (fleft( x right) =  — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: 6.
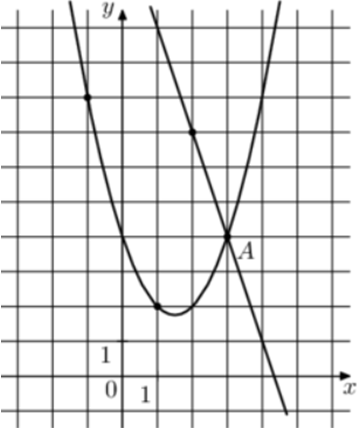
Задача 25. На рисунке изображены графики функций (fleft( x right) =  — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 22.
Задача 26. На рисунке изображены графики функций (fleft( x right) =  — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 26.
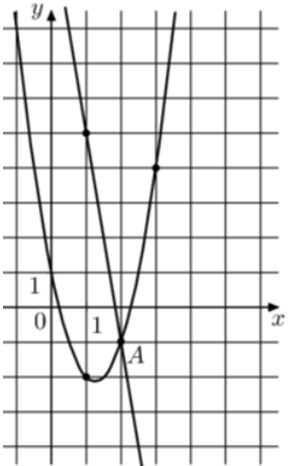Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 23.
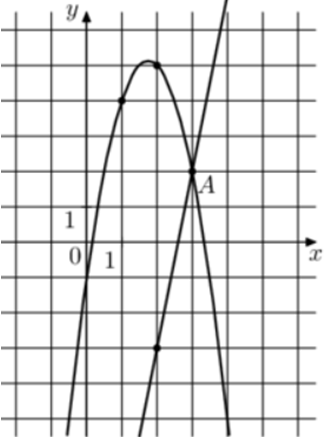Задача 28. На рисунке изображены графики функций (fleft( x right) =  — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 16.
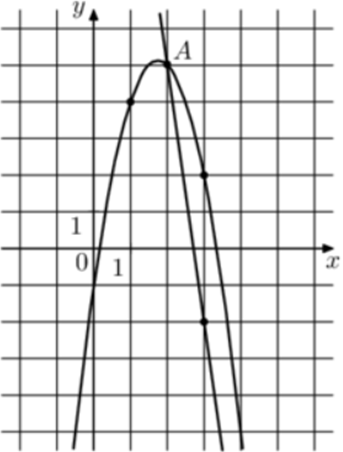Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6.
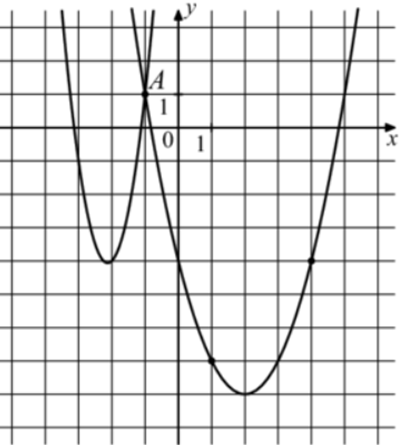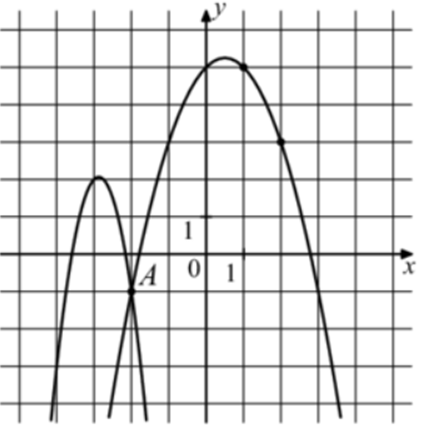
Задача 30. На рисунке изображены графики функций (fleft( x right) =  — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите абсциссу точки B.

Ответ

ОТВЕТ: — 6.
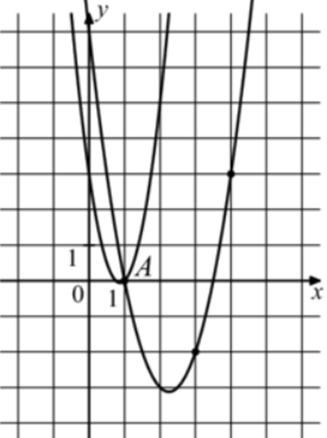
Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: 33.
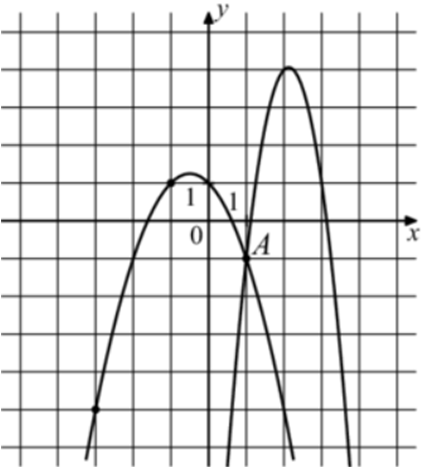
Задача 32. На рисунке изображены графики функций (fleft( x right) =  — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,)  которые пересекаются в точках  A и B. Найдите ординату точки B.

Ответ

ОТВЕТ: — 29.

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции fleft(xright)=kx+b. Найдите значение x, при котором fleft(xright)=-13,5.

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..

Вычтем из первого уравнения второе:

left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .

Уравнение прямой имеет вид:

displaystyle y=frac{7}{4}x-frac{5}{4}.

Найдем, при каком x значение функции равно -13,5.

displaystyle frac{7}{4}x-frac{5}{4}=-13,5;

7x-5=-54;

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой: y=-5x-6.

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен displaystyle frac{3}{2}=1,5.

Эта прямая проходит через точку (-2; 4), поэтому: 1,5cdot left(-2right)+b=4; b=7, эта прямая задается формулой y=1,5x+7.

Для точки пересечения прямых:

x+1=1,5x+7;

0,5x=-6;

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции y=ax^2+bx+c. Найдите b.

Решение:

На рисунке — квадратичная парабола y={left(x-aright)}^2, полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: fleft(xright)={left(x-1right)}^2=x^2-2x+1;

b=-2.

Ответ: -2.

5. На рисунке изображен график функции y={left(x-cright)}^2. Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид y={left(x-1right)}^2.

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции fleft(xright)=2x^2+bx+c. Найдите fleft(-5right).

Решение:

График функции y=2x^2+bx+c проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .

left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right. отсюда b=3, c=-4.

Формула функции имеет вид:

fleft(xright)=2x^2+3x-4;

fleft(-5right)=2cdot 25-3cdot 5-4=31.

Ответ: 31.

7. На рисунке изображены графики функций fleft(xright)=5x+9 и gleft(xright)=ax^2+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции gleft(xright)=ax^2+bx+c. График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right. отсюда a=b=1;

gleft(xright)=x^2+x-3;

Найдем абсциссу точки B. Для точек A и B: fleft(xright)=g(x)

5x+9=x^2+x-3;

x^2-4x-12=0.

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций displaystyle fleft(xright)=frac{k}{x} и gleft(xright)=ax+b, которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции displaystyle y=frac{k}{x} проходит через точку (2; 1); значит, displaystyle frac{k}{2}=1;

displaystyle k=2, ; fleft(xright)=frac{2}{x}.

График функции gleft(xright)=ax+b проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда 5cdot 2+b=1; b=-9.

Для точек A и B имеем: fleft(xright)=gleft(xright);

displaystyle frac{2}{x}=5x-9;

5x^2-9x-2=0.

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции fleft(xright)=ksqrt{x}. Найдите f (6,76).

Решение:

Функция задана формулой:

y=ksqrt{x}. Ее график проходит через точку (4; 5); значит, kcdot sqrt{4}=5; k=2,5;

fleft(xright)=2,5sqrt{x}. Тогда fleft(6,76right)=2,5cdot sqrt{6,76}=2,5cdot 2,6=6,5.

Ответ: 6,5.

10. На рисунке изображен график функции fleft(xright)=sqrt{ax}. Найдите fleft(-25right).

Решение:

График функции на рисунке симметричен графику функции y=sqrt{x} относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: y=sqrt{-x}, а = — 1. Тогда fleft(-25right)=sqrt{25} = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции fleft(xright)=a^{x+b}. Найдите fleft(-7right).

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции fleft(xright)=a^{x+b}, получим:

left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.

Поделим второе уравнение на первое:

a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.

Подставим во второе уравнение:

displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.

displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.

Ответ: 0,25.

12. На рисунке изображен график функции y=acdot 4^x. Найдите a.

Решение:

График функции y=acdot 4^x проходит через точку left(0;2right). Это значит, что yleft(0right)=2;

acdot 4^0=2; a=2, формула функции имеет вид: y=2cdot 4^x.

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции fleft(xright)={{log}_a left(x+bright)}. Найдите fleft(11right).

Решение:

График функции y={{log}_a left(x+bright) } проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.

Отсюда: left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.

Вычтем из второго уравнения первое:

a^2-a=2; a^2-a-2=0;

a=2 или a=-1 — не подходит, так как a textgreater 0 (как основание логарифма).

Тогда b=a+3=5; fleft(xright)={{log}_2 left(x+5right) };

fleft(11right)={{log}_2 16=4.}

Ответ: 4.

14. На рисунке изображен график функции fleft(xright)=a{{log}_5 x }-c.

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки left(1;-2right) и left(5;3right). Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.

left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.

left{ begin{array}{c}c=2 \a=5 end{array}.right.

Формула функции: fleft(xright)=5{{log}_5 x }-2.

Найдем displaystyle fleft(0,2right)=fleft(frac{1}{5}right) :

displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции fleft(xright)=a{sin x }+b. Найдите b.

Решение:

График функции y=a{sin x+b } сдвинут на 1,5 вверх; fleft(0right)=1,5. Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции fleft(xright)=2{sin x }+1,5. Он получен из графика функции y={sin x } растяжением в 2 раза по вертикали и сдвигом вверх на 1,5.

Ответ: b=1,5.

16. На рисунке изображён график функции

fleft(xright)=a tgx+b.

Найдите a.

Решение:

На рисунке — график функции fleft(xright)=a tgx+b. Так как fleft(0right)=-1,5, b=-1,5.

График функции проходит через точку A displaystyle (frac{pi}{4}; ; frac{1}{2}). Подставим b = - 1,5 и координаты точки А в формулу функции.

displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.

Так как displaystyle tg frac{pi}{4}=1, получим: a = 2.

Ответ: 2.

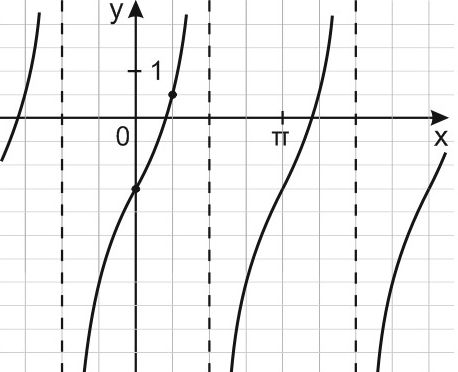
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения f (21)- f (-9).

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если yleft(1right)=2,5, то yleft(-1right)=-2,5.

Пользуясь периодичностью функции fleft(xright) , период которой T = 4, получим:

fleft(21right)=fleft(1+4cdot 5right)=fleft(1right)=2,5;

fleft(-9right)=fleft(-1-4cdot 2right)=fleft(-1right)=-2,5;

fleft(21right)-fleft(-9right)=2,5-left(-2,5right)=5.

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Решу ЕГЭ 2022 задание №9 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки к экзамену.

  • скачать задания прямая с ответами
  • скачать задания парабола с ответами
  • скачать задания гипербола с ответами
  • скачать задания логарифмические функции с ответами
  • скачать задания иррациональные функции с ответами
  • скачать задания тригонометрические функции с ответами

Решу ЕГЭ 2022 линейные функции 9 задание математика с ответами:

Решу ЕГЭ 2022 парабола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 гипербола 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 логарифмические функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 иррациональные функции 9 задание профиль математика с ответами:

Решу ЕГЭ 2022 тригонометрические функции 9 задание профиль математика с ответами:

Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Как решать 9 задание ЕГЭ 2022 математика профиль видео теория:



1)На рисунке изображён график функции вида f(x)= a3x+b x+c , где числа a, b и c — целые. Найдите a.

2)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

3)На рисунке изображён график функции вида f(x)= ax+b x+c , где числа a, b и c — целые. Найдите a.

4)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(−22).

5)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.

6)На рисунке изображён график функции вида f(x)= 2ax+b x+c , где числа a, b и c — целые. Найдите a.

7)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(15).

8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.

9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c  — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.

10)На рисунке изображён график функции вида f(x)=log1.4(x−a)+b, где числа a, b  — целые. Найдите ab.

11)На рисунке изображён график функции вида f(x)=2ax+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если f(1)=10.

12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b  — целые. Найдите сумму коэффициентов a+b.

13)На рисунке изображён график функции вида f(x)=ln(a+x)+b, где числа a, b  — целые. Найдите сумму коэффициентов a+b, если A(0;ln2e).

Задание №3 ЕГЭ 2022 по математике профиль прототипы с ответами

Задание №4 ЕГЭ 2022 по математике профиль прототипы с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

На рисунке изображены графики функций f(x)=-2x²-2x+4 и g(x)=ax²+bx+c, которые пересекаются в точках A(-1;4) и В(х₀;y₀). Найдите х₀.

ЕГЭ № 9 две параболы

Решение:

 Правая парабола пересекает ось y в точке (0;4), значит, ее уравнение задается следующей формулой: f(x)=-2x²-2x+4

Левая парабола пересекает ось y в точке (0;1), значит ее уравнение задается следующей формулой: g(x)=ax²+bx+1

Функция g(x) проходит через точку (-4;1), значит:

1=16a-4b+1

16a-4b=0

16a=4b

b=4a     (1)

Функция g(x) проходит через точку (-1;4), значит:

4=a-b+1

a-b=3     (2)

Подставим (1) в (2) и найдем а:

a-4a=3

-3a=3

a=-1

Найдем b, подставив a=-1 в (1):

b=-4

Имеем следующее:

f(x) =2x²+3x-4,

g(x) =-x²-4x+1.

Так как функции пересекаются, то f(x) = g(x):

-2x²-2x+4 = -x²-4x+1

x²-2x-3=0

D = (-2)² – 4·1·(-3) =4 + 12 = 16

x₁ = х₀ = 3 – абсцисса точки В,

x₂ = -1 – абсцисса точки А.

Ответ: 3

Источник

Графики функций Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

Графики функций

Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

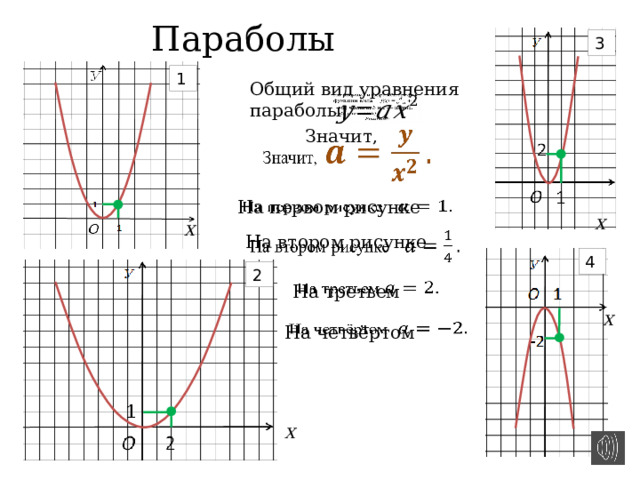
Параболы 3 1 Общий вид уравнения параболы     Значит ,   На первом рисунке X X На втором рисунке   4 2 На третьем   X На четвёртом   X

Параболы

3

1

Общий вид уравнения параболы

Значит ,

На первом рисунке

X

X

На втором рисунке

4

2

На третьем

X

На четвёртом

X

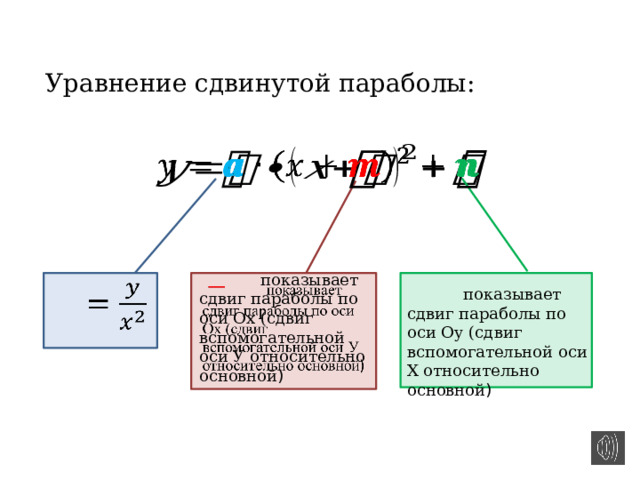
Уравнение сдвинутой параболы:           показывает сдвиг параболы по оси Ох (сдвиг вспомогательной оси У относительно основной )   показывает сдвиг параболы по оси Оу (сдвиг вспомогательной оси Х относительно основной )

Уравнение сдвинутой параболы:

показывает сдвиг параболы по оси Ох (сдвиг вспомогательной оси У относительно основной )

показывает сдвиг параболы по оси Оу (сдвиг вспомогательной оси Х относительно основной )

Пример   2 На рисунке изображён график функции вида  где числа  a ,  b  и  c  — целые. Найдите значение  .   -1 Решение По уравнению видно, что представленный график является параболой.   Общий вид уравнения сдвинутой параболы             Ответ: 6,4375

Пример

2

На рисунке изображён график функции вида 

где числа  a ,  b  и  c  — целые. Найдите значение  .

-1

Решение

По уравнению видно, что представленный график является параболой.

Общий вид уравнения сдвинутой параболы

Ответ: 6,4375

Источник

Понравилась статья? Поделить с друзьями:
  • Решение 8 задания егэ по русскому языку онлайн
  • Решение 6 варианта егэ по физике 2023 демидова
  • Решение 5 варианта егэ по математике 2022 ященко 36 вариантов ответы с решением профильный
  • Решение 4 задания егэ информатика на python
  • Решение 34 задачи химия егэ 2020