Решение варианта 15 егэ математика ященко 2022 года 36 вариантов - Помощь в подготовке к экзаменам и поступлению

Скрыть

Пусть $$S$$ рублей – начальная сумма кредита. По условию сумма долга должна равномерно уменьшаться каждый месяц и на 24-й составлять 0 рублей, то есть, имеем последовательность долга по месяцам:

$$S,frac{23}{24}S,frac{22}{24}S,cdots,frac{10}{24}S,cdots,frac{1}{24}S,0$$

Далее, в начале каждого месяца долг возрастает на 1%, имеем последовательность перед выплатой:

$$1,01S;1,01cdotfrac{23}{24}S;1,01cdotfrac{22}{24}S;cdots;1,01cdotfrac{1}{24}S$$

Следовательно, сами выплаты по месяцам должны быть равны:

$$m_1=1,01S-frac{23}{24}S=frac{1}{24}S+0,01S$$

$$m_2=1,01cdotfrac{23}{24}S-frac{22}{24}S=frac{1}{24}S+0,01cdotfrac{23}{24}S$$

$$cdots$$

$$m_{23}=1,01cdotfrac{2}{24}S-frac{1}{24}S=frac{1}{24}S+0,01cdotfrac{2}{24}S$$

$$m_{24}=1,01cdotfrac{1}{24}S-0=frac{1}{24}S+0,01cdotfrac{1}{24}S$$

Известно, что за 15-й месяц выплаты составили 44 тыс. рублей, то есть:

$$m_{15}=frac{1}{24}S+0,01cdotfrac{10}{24}S=44000$$

Откуда

$$S=frac{24cdot44000}{1,1}=960000$$

И общая сумма возврата, равна:

$$(frac{S}{24}+0,01S)+(frac{S}{24}+0,01cdotfrac{23}{24}S)+cdots+(frac{S}{24}+0,01cdotfrac{1}{24}S)=$$

$$S+frac{0,01S}{24}cdotfrac{(24+1)cdot24}{2}=S+frac{0,25S}{2}$$

Подставляем числовые значения, получаем:

$$960000+frac{0,25cdot960000}{2}=1080000$$

Источник


3221	Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,4? Решение	Стрелок в тире стреляет по мишени до тех пор, пока не поразит её ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 10

2607	В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется чёрной, равна 0,37, а того, что она окажется синей, равна 0,45. Найдите вероятность того, что ручка окажется красной Решение	В магазине в одной коробке лежат вперемешку ручки ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 2 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 4

2554	Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут, а одна первая труба наполняет бассейн за 40 часов. За сколько часов наполняет бассейн одна вторая труба? Решение	Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 11

2553	Найдите точку максимума функции y=-(x^2+196)/x Решение График	Найдите точку максимума функции y= -(x^2 + 196) / x ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 11 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 12

2551	У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 10 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 15 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая. a) Может ли у Миши быть 30 монет? б) Какое наибольшее количество монет может быть у Миши? в) Какая наибольшая сумма рублей может быть у Миши? Решение	У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 19

2550	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4, а боковое ребро AA1 равно 5sqrt3. На ребре DD1 отмечена точка M так, что DM:MD1=3:2. Плоскость alpha параллельна прямой A1F1 и проходит через точки M и E. а) Докажите, что сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha — равнобедренная трапеция. б) Найдите объём пирамиды, вершиной которой является точка F, а основанием — сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha Решение	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 14

2549	а) Решите уравнение sin^4(x/4)-cos^4(x/4)=cos(x-pi/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/2; pi]. Решение График	Решите уравнение sin^4(x/4) -cos^4(x/4) = cos(x-pi/2) ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 12 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 13

2548	Решите неравенство (20.5^(x+2)-0.52^(x+2)). (2log_{0.5)^2(x+2)-0.5log_{2}(x+2)) <= 0. Решение График	Решите неравенство (20.5^(x+2)- 0.52^(x+ 2)) (2log^2_{0.5)(x+2)- 0.5log_{2}(x+ 2)) <= 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 14 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 15

Источник

Решение и ответы заданий Варианта №15 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Задание 1.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.

Задание 2.
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.

Задание 3.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.

Задание 4.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 5.
Найдите корень уравнения sqrt{9-8x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Задание 6.
Найдите значение выражения frac{2^{log_{9}3}}{2^{log_{9}243}}.

Задание 7.
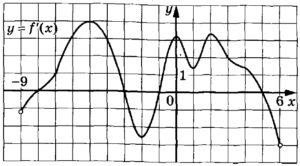
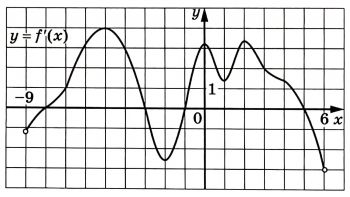
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

Задание 8.
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v₀ = 1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с². Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.

Задание 9.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

Задание 10.
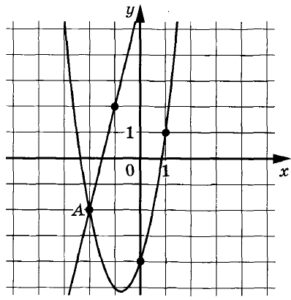
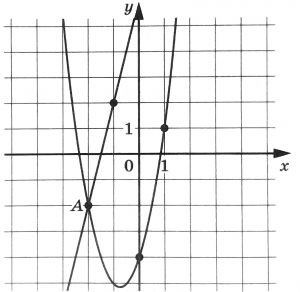
На рисунке изображены функций графики f(x) = ах² + bх + с и g(x) = kx + d, которые пересекаются в точках А и В. Найдите абсциссу точки В.

Задание 11.
Найдите наибольшее значение функции у = х⁵ + 5х³ – 140х на отрезке [–8; –1].

Задание 12.
а) Решите уравнение sin2x + cos2x = 1.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; –2pi].

Задание 13.
В правильной призме ABCDA₁B₁C₁D₁ с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А₁ перпендикулярно плоскости AB₁D₁ проведена прямая l.

а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми l и СВ₁.

Задание 14.
Решите неравенство 7^{log_{frac{1}{7}}log_{frac{1}{2}}(–x)}< 2^{log_{frac{1}{2}}log_{frac{1}{7}}(–x)}.

Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
– в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
– в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.

Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{12}{49} площади трапеции ABCD.

Задание 17.
Найдите все такие значения а, при каждом из которых неравенство

–1 ≤ sinx(a – cos2x) ≤ 1

верно при всех действительных значениях х.

Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.

а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?

Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Решение 15 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023

Скачать сборник в pdf

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.

Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.

При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.

Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решите уравнение (sqrt{9-8x}=-x). Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Найдите значение выражения (dfrac{2^{log_93}}{2^{log_9243}})

На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

Груз массой 0,25 кг колеблется на пружине. Его скорость (v) меняется по закону (v = v_0 cosdfrac{2pi t}{T}), где (t) – время с момента начала колебаний, (T= 2) с – период колебаний, (v_0= 1{,}6) м/с. Кинетическая энергия (E) (в джоулях) груза вычисляется по формуле (E = dfrac{mv^2}{2}), где (m) – масса груза в килограммах, (v) – скорость груза в м/с. Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.

Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

На рисунке изображены графики функций (f(x)=ax^2+bx+c) и (g(x)=kx+d), которые пересекаются в точках А и В. Найдите абсциссу точки В.

Найдите наибольшее значение функции ( y=x^5+5x^3-140x ) на отрезке (left[-8;-1right])

а) Решите уравнение (sin{2x}+cos{2x}=1).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{7pi}{2};-2piright] ).

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)

1. 2πn, n∈Z	2. π/6+2πn, n∈Z	3. π/4+2πn, n∈Z	4.π/3+2πn, n∈Z
5. π/2+2πn, n∈Z	6. 2π/3+2πn, n∈Z	7. 3π/4+2πn, n∈Z	8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z	10. -π/6+2πn, n∈Z	11. -π/4+2πn, n∈Z	12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z	14. -2π/3+2πn, n∈Z	15. -3π/4+2πn, n∈Z	16. -5π/6+2πn, n∈Z

б)

17. -7π/2	18. -10π/3	19. -13π/4	20. -19π/6
21. -3π	22. -17π/6	23. -11π/4	24. -8π/3
25. -5π/2	26. -7π/3	27. -9π/4	28. -13π/6
29. -2π

В правильной призме ABCDA₁B₁C₁D₁ с основанием ABCD боковое ребро равно (sqrt{3}) , а сторона основания равна 2. Через точку А₁ перпендикулярно плоскости AB₁D₁ проведена прямая (l).
а) Докажите, что прямая (l) пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми (l) и СВ₁.

Решите неравенство ( 7^{log_{frac{1}{7}}{log_{frac{1}{2}}{left(-xright)}}}< 2^{log_{frac{1}{2}}{log_{frac{1}{7}}{left(-xright)}}} )

В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на 20% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.

Около окружности с центром (O) описана трапеция (ABCD) с основаниями (AD) и (BC).
а) Докажите, что (angle AOB = angle COD = 90^{circ}).
б) Найдите отношение большего основания трапеции к меньшему, если известно, что (AB = CD), а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет (dfrac{12}{49}) площади трапеции (ABCD).

Найдите все такие значения (a), при каждом из которых неравенство (-1leqslantsin x(a-cos2x)leqslant1) верно при всех действительных значениях (x).

Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Источник

Mat-EGE.ru >> Все варианты ОГЭ-2022 >> Вариант № 15

Поделиться Вконтакте

ПОДПИСАТЬСЯ (YOUTUBE)

№ задания:

Источник

Новый стрим, новый Ященко! Разбираем уравнения и неравенства из Сборника ЕГЭ-2022!

Приветствуем, друзья!

1. Заканчивается распродажа для преподавателей. Сегодня очередное подорожание онлайн-курса.

2. Многие из вас готовятся к ЕГЭ по Сборникам тренировочных вариантов ЕГЭ под редакцией И. В. Ященко. И возможно, не всё сразу получается.

Чтобы помочь вам, на стриме в четверг, 18 ноября, Анна Малкова уравнения и неравенства из Сборника «36 тренировочных вариантов ЕГЭ-2022».

Регистрируйтесь на стрим, это бесплатно!

ЖДЕМ НА СТРИМЕ!

Что будет на стриме?

Разберем задания 12 и 14 из сборника Ященко 2022 года.

Еще раз поговорим о решении и оформлении тригонометрических уравнений. Об отборе корней.

Основная тема – все-таки неравенства. Показательные, логарифмические, комбинированные.

Повторим, что такое логарифмы, и основные формулы для логарифмов.

Вспомним, что писать на бланке ЕГЭ, когда мы «отбрасываем логарифмы» (про «отбрасывание» или «откидывание» писать не надо!).

Поговорим об оформлении. Как должно выглядеть ваше решение, чтобы вы получили за него максимальный балл.

И о том, чего точно не нужно делать. Если, конечно, не хотите растерять баллы.

Стрим ведет Анна Малкова. 18 ноября, в 17.00 по московскому времени.

Регистрируемся и смотрим!

Как готовиться по Ященко?

Стоит ли готовиться к ЕГЭ-2022 по новому сборнику «36 тренировочных вариантов» под редакцией И. В. Ященко?

Наше мнение: сборник пригодится учителям и репетиторам.

Но готовиться по нему к ЕГЭ самостоятельно мы не рекомендуем.

И вот почему:

1) Задачи в вариантах неравноценны по сложности. Например, в одном варианте простейшее неравенство в № 14, в другом – сложное комбинированное.

2) Особенно это заметно для задачи 10 по теории вероятностей (новая задача). В одних вариантах – простейшие, хорошо всем знакомые задачи, например, про стекла для автомобильных фар. В других – задача про викторину, которая оказалась сложной даже для опытных преподавателей. Кстати, ее решение на этой странице под №10.

3) Решения даны только к вариантам 1, 7, 11, 17, 21, 27, 31 (7 из 36).

И вообще готовиться к ЕГЭ по сборнику заданий – плохая идея. Обычно это означает, что вы «выгрызаете» из каждого варианта несколько простых заданий, например, 6 штук из 18 задач каждого вариант. И говорите: ну вот, за пару дней прорешал треть сборника. Еще 4 дня – и подготовлюсь полностью

Но почему-то так не происходит. И что делать со сложными задачами – непонятно. И сборник отправляется на полку.

Оптимальная отработанная подготовка

А как же надо готовиться к ЕГЭ?

Сначала – выучить необходимую теорию. Посмотреть, как решаются задачи такого типа. Затем самостоятельно работать над темой, от простых задач к сложным, и так, чтобы получать не только ответы, но и подробные решения.

Решать варианты – только на заключительном этапе тренировки!

Именно так построено обучение на Онлайн-курсе Анны Малковой.

Необходимая теория, написанная простым и понятным языком.

Видеоучебник. Как решать задачи, на что обратить внимание.

Прямые трансляции 2 раза в неделю. По 120 минут. Как с репетитором. По всем темам и задачам Профильного ЕГЭ по математике.

Онлайн-тренажер (72 темы). Все задачи – с подробными решениями и ответами.

Ответы на все ваши вопросы, помощь в решении задач.

И Пробные ЕГЭ раз в месяц.

Кстати, пора присылать решения на наш Ноябрьский Пробный ЕГЭ. Кто он нем еще не знает – читаем и регистрируемся, здесь! Это бесплатно!

Смотрим стрим Анны Малковой завтра. И идем к нам на Онлайн-курс! Это лучше, чем самостоятельно пытаться подготовиться по сборнику Ященко.

Наши Онлайн-курсы:

Для тех, кому нужна выстроенная, проверенная программа подготовки от опытных преподавателей. С нуля до самых сложных тем. Есть программы для абитуриентов и преподавателей. Посмотрите видео, как устроен курс. Оформите бесплатный демодоступ.

Математика

Физика

Информатика

Русский

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Разбираем сборник Ященко-2022!» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из Рубрики: Новости.

Публикация обновлена:
10.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Источник

Задание 15. Вариант 8 ЕГЭ 2022 Ященко из 36 вариантов

Задание 15. Производство х тыс. единиц продукции обходится в млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет . При каком наименьшем значении p через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении x?

Решение.

Годовая прибыль компании составляет:

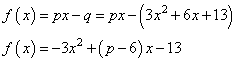
Это график параболы с точкой максимума:

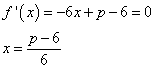
И наибольшее значение годовой прибыли достигает при

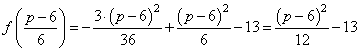
Нужно найти наименьшее p при котором суммарная прибыль за 5 лет составит не менее 70 млн рублей:

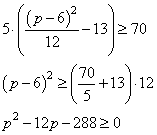
Решаем квадратное уравнение, имеем:

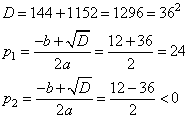
Равенство в 70 млн рублей достигается при p = 24.

Ответ: 24

Источник