Скрыть
а) Заметим, что прямые EH и E1H1 параллельны, следовательно, плоскость α пересекает нижнее основание трапеции по прямой, параллельной EH и содержащей точку A. Такой прямой является прямая, cодержащая диагональ AD основания, то есть AD — сторона сечения. Вторая сторона сечения это отрезок DM. Плоскости ABC и BCC1 пересекаются по прямой CB, параллельной AD, следовательно, плоскость α пересекает плоскость BCC1 по прямой, параллельной ребру двугранного угла DBCM, то есть параллельной BC. Назовем эту прямую MN, где N лежит на ребре BB1.
Таким образом, прямые AD, BC и MN параллельны между собой. Кроме того, $$MN=BCneq AD,$$ следовательно, ADMN — трапеция. Легко заметить, что треугольники ABN и DCM равны и, следовательно, $$AN=DM.$$
б) Построим сечение призмы, проходящее через точки P, Q, R и S — середины ребер BC, B1C1, F1G1 и FG, соответственно. Очевидно, что указанное сечение проходит также через точки K и L — середины AD и MN, а также перпендикулярно этим отрезкам.
Заметим, что прямые F1G1, E1H1 и плоскость α параллельны между собой, следовательно, расстояния до плоскости α от всех точек этой прямой равны. Из точки R на прямую KL опустим перпендикуляр RO, заметим, что прямые RO и AD взаимно перпендикулярны, следовательно, прямая RO перпендикулярна плоскости α.
Расстояние от точки F до плоскости равно длине RO. Пусть T — точка пересечения RO и PS. Значит,
$$LP=MC=frac{1}{3}CC_1=2,$$
откуда
$$KP=3,KL=sqrt{13},MN=BC=3sqrt{2},AD=3sqrt{2}+6$$
Теперь можно найти площадь трапеции ADMN: $$S_{ADMN}=3sqrt{13}(sqrt{2}+1).$$
Заметим, что треугольники LPK, KTO и RTS — подобны. Следовательно,
$$frac{ST}{RS}=frac{LP}{PK}=frac{2}{3},$$
откуда
$$ST=4,SP=AD=3sqrt{2}+6,TK=3sqrt{2}-1,RT=2sqrt{13},$$
тогда
$$frac{TO}{LP}=frac{TK}{KL}=frac{3sqrt{2}-1}{sqrt{13}}Rightarrow TO=frac{2(3sqrt{2}-1}{sqrt{13}}.$$
Итак,
$$RO=RT+TD=frac{6(sqrt{2}+4)}{sqrt{13}},$$
а значит, объем пирамиды F1ADMN равен
$$V_{F_1ADMN}=frac{1}{3}ROcdot S_{ADMN}=6(5sqrt{2}+6)$$
| 3282 | Отрезок, соединяющий середины M и N оснований ВC и AD соответственно трапеции ABCD разбивает её на две трапеции, в каждую из которых можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Известно, что радиус этих окружностей равен 4, а меньшее основание BC исходной трапеции равно 14. Найдите радиус окружности, касающейся боковой стороны AB, основания AN трапеции ABMN и вписанной в неё окружности |
а) Докажите, что трапеция ABCD равнобедренная ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 16 # Задачи-Аналоги 937 262 | |
| 3245 | В правильной восьмиугольной призме ABCDEFGHA1B1C1D1E1F1G1H1 сторона основания AB равна 3sqrt2, а боковое ребро AA1 равно 6. На ребре CC1 отмечена точка M так, что CM:MC1=1:2. Плоскость alpha параллельна прямой H1E1 и проходит через точки M и A. а) Докажите, что сечение призмы ABCDEFGHA1B1C1D1E1F1G1H1 плоскостью alpha — равнобедренная трапеция. б) Найдите объём пирамиды, вершиной которой является точка F1, а основанием — сечение призмы ABCDEFGHA1B1C1D1E1F1G1H1 плоскостью alpha |
В правильной восьмиугольной призме ABCDEFGHA1B1C1D1E1F1G1H1 сторона основания AB равна 3 корня из 2, а боковое ребро AA1 равно 6 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 19 Задание 13 | |
| 2600 | Найдите наименьшее значение функции y=x*sqrt(x)-6x+11 на отрезке [0; 30] |
Найдите наименьшее значение функции y=x корней из x — 6x + 11 ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 11 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 9 Задание 12 | |
| 2599 | Даны два цилиндра. Объём первого цилиндра равен 5. У второго цилиндра высота в 2,5 раза меньше, а радиус основания в 3 раза больше, чем у первого. Найдите объём второго цилиндра |
Даны два цилиндра ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 5 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 9 Задание 8 | |
| 2598 | Смешали 2 кг воды с 3 кг 32-процентного раствора и некоторым количеством 42-процентного раствора одного и того же вещества. Сколько килограммов 42-процентного раствора использовали, если в результате получили 32-процентный раствор вещества? |
Смешали 2 кг воды с 3 кг 32-процентного раствора и некоторым количеством 42-процентного раствора ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 8 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 9 Задание 11 | |
| 2595 | а) Решите уравнение cos(3x)*sin(3x)=cos(pi/3)*cos(12x+(3pi)/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/4; -pi/4]. |
Решите уравнение cos(3x)* sin(3x)= cos(pi/3)* cos(12x+ (3pi)/2 ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 12 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 9 Задание 13 | |
| 2594 | Решите неравенство 9*2^(log_{3}(5-x))+2^(1+log_{3}(x))-2^(log_{3}(5x-x^2)) <= 18 |
Решите неравенство 9*2 в степени log 3 5-x +2 в степени 1+ log 3 x -2 в степени log 3 5x -x^2 <= 18 ! 36 вариантов ФИПИ Ященко 2022 Вариант 19 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 9 Задание 15 | |
| Clear |
Напиши мне, решений каких вариантов не хватает на сайте?
Например: «Сборник Лысенко ЕГЭ 2023 профиль 40 вариантов», «Варианты Ларина ЕГЭ 2023 профиль», «Варианты СтатГрад ЕГЭ 2023 профиль» и т.п.
Варианты СтатГрад ЕГЭ 2023 (профильный уровень)
Варианты сборника И.В. Ященко ЕГЭ 2023 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2022 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2021 (профильный уровень), 36 вариантов.
Варианты сборника Ф.Ф. Лысенко ЕГЭ 2021 (профильный уровень), 40 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2020 (профильный уровень), 36 вариантов.
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36
На счету Юлиного мобильного телефона было 93 рубля, а после разговора с Мишей осталось 28 рублей. Сколько минут длился разговор с Мишей, если одна минута разговора стоит 2 рубля 50 копеек?
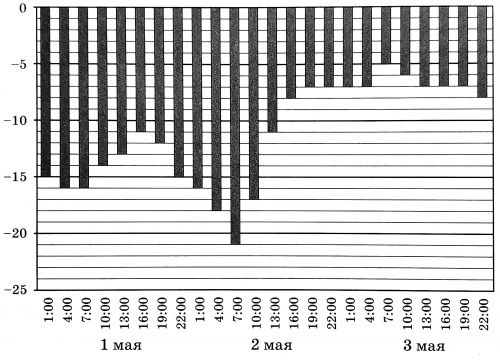
На диаграмме показаны значения температуры в Норильске с 1 по 3 мая 2019 года. По горизонтали указаны моменты измерений, по вертикали — температура в градусах Цельсия. Определите по диаграмме значение наибольшей температуры в Норильске 1 мая.
Точки O(0; 0), A(23; 0), B(20; 18), C(3; 18) являются вершинами трапеции. Найдите длину её средней линии.
Вероятность того, что новый фен прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Найдите корень уравнения (log_{2}{(8-x)}=2log_{2}{(4+x)}). Если уравнение имеет более одного корня, в ответе запишите наименьший из корней.
В треугольнике со сторонами 8 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 1. Чему равна высота, проведённая ко второй стороне?
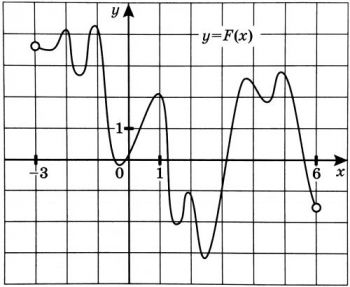
На рисунке изображён график функции (y=F(x)) — одной из первообразных функции (f(x)) определённой на интервале ((-3; 6)). Найдите количество решений уравнения (f(x)=0) на отрезке ([-2; 5]).
Шар, объём которого равен 64, вписан в цилиндр. Найдите объём цилиндра.
Найдите значение выражения (dfrac{left(2^{frac{4}{7}}cdot3^{frac{2}{3}}right)^{21}}{6^{12}}).
Груз массой (0{,}3) кг колеблется на пружине. Его скорость (v) меняется по закону (v=v_0cosdfrac{2pi t}{T}), где (t) — время с момента начала колебаний, (Т=2) с — период колебаний, (v_0=0{,}2) м/с. Кинетическая энергия (E) (в джоулях) груза вычисляется по формуле (E=dfrac{mv^2}{2}), где (m) — масса груза в килограммах, (v) — скорость груза в м/с. Найдите кинетическую энергию груза через 33 с после начала колебаний. Ответ дайте в джоулях.
На изготовление 33 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 77 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
Найдите наименьшее значение функции (y=2x^2-5x+ln x-5) на отрезке (left[dfrac{5}{6};dfrac{7}{6}right]).
а) Решите уравнение (8^{cos^2{x}}=left(sqrt{2}right)^{5sin{2x}}cdot0{,}5)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[dfrac{5pi}{2};4piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. (pi n,; ninmathbb{Z}) | 2. (dfrac{pi}{6}+pi n,; ninmathbb{Z}) | 3. (dfrac{pi}{4}+pi n,; ninmathbb{Z}) | 4. (dfrac{pi}{3}+pi n,; ninmathbb{Z}) |
| 5. (dfrac{pi}{2}+pi n,; ninmathbb{Z}) | 6. (dfrac{2pi}{3}+pi n,; ninmathbb{Z}) | 7. (dfrac{3pi}{4}+pi n,; ninmathbb{Z}) | 8. (dfrac{5pi}{6}+pi n,; ninmathbb{Z}) |
| 9. (mathrm{arctg,}2+pi n,; ninmathbb{Z}) | 10. (mathrm{arctg,}3+pi n,; ninmathbb{Z}) | 11. (mathrm{arctg,}4+pi n,; ninmathbb{Z}) | 12. (mathrm{arctg,}5+pi n,; ninmathbb{Z}) |
| 13. (-mathrm{arctg,}2+pi n,; ninmathbb{Z}) | 14. (-mathrm{arctg,}3+pi n,; ninmathbb{Z}) | 15. (-mathrm{arctg,}4+pi n,; ninmathbb{Z}) | 16. (-mathrm{arctg,}5+pi n,; ninmathbb{Z}) |
б)
| 17. (dfrac{5pi}{2}) | 18. (dfrac{8pi}{3}) | 19. (dfrac{11pi}{4}) | 20. (dfrac{17pi}{6}) |
| 21. (3pi) | 22. (dfrac{19pi}{6}) | 23. (dfrac{13pi}{4}) | 24. (dfrac{10pi}{3}) |
| 25. (dfrac{7pi}{2}) | 26. (dfrac{11pi}{3}) | 27. (dfrac{15pi}{4}) | 28. (dfrac{23pi}{6}) |
| 29. (4pi) | 30. (mathrm{arctg,}2+3pi) | 31. (mathrm{arctg,}3+3pi) | 32. (mathrm{arctg,}4+3pi) |
| 33. (-mathrm{arctg,}2+4pi) | 34. (-mathrm{arctg,}3+4pi) | 35. (-mathrm{arctg,}4+4pi) |
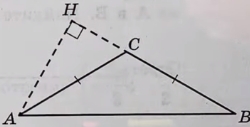
Основание пирамиды (SABC) – равносторонний треугольник (ABC). Боковое ребро (SA) перпендикулярно плоскости основания, точки (M) и (N) — середины рёбер (BC) и (AB) соответственно, причём (SN=AM).
а) Докажите, что угол между прямыми (AM) и (SN) равен (60°).
б)Найдите расстояние между этими прямыми, если (BC=3sqrt{2}).
Решите неравенство (4^{2x+1{,}5}-9^{x+0{,}5}geqslant2cdot12^x)
В треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке F. Отрезок BD — диаметр этой окружности.
а) Докажите, что AD=CF.
б) Найдите DF, если радиус описанной около треугольника ABC окружности равен 12, угол BAC=35°, угол ACB=65°.
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 14% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 3,249 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения (a), при каждом из которых уравнение (dfrac{x^2+x+a}{x^2-2x+a^2+6a}=0) имеет ровно два различных корня.
Сторона квадрата на 3 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
а) Может ли ширина прямоугольника быть равной 8?
б) Может ли длина прямоугольника быть равной 16?
в) Найдите все возможные варианты таких пар прямоугольников и квадратов.
Введите ответ в форме строки «да;да;1;2;3;4». Где ответы на пункты разделены «;», первые два ответа с маленькой буквы, а в пункте В перечислите возможные длины стороны квадрата по возрастанию через точку с запятой.
- ОГЭ по математике
Полный разбор вариантов ОГЭ 2022 по математике — сборник ФИПИ школе Ященко 36 вариантов.
Подробный разбор всех заданий.
Решение варианта 1
Решение варианта 2
Разбор всех вариантов смотрите здесь.
Серия книг ФИПИ школе подготовлена разработчиками контрольных измерительных материалов (КИМ) основного государственного экзамена.
В сборнике представлены:
— 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ОГЭ по математике 2022 года;
— инструкция по выполнению работы;
— ответы ко всем заданиям;
— решения и критерии оценивания заданий части 2.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации в 9 классе, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ основного общего образования и интенсивной подготовки обучающихся к ОГЭ.
Купить ОГЭ 2022. Математика. Типовые экзаменационные варианты. 36 вариантов
Смотрите также:
ЕГЭ 2022, полный разбор 1 варианта Ященко ФИПИ школе 36 вариантов. Решаем типовые варианты от Ященко 2022 года ЕГЭ профиль!
Решаем 1 вариант Ященко 2022 года сборника ФИПИ школе 36 вариантов. Разбор 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 задания.
Больше разборов на моем ютуб-канале
Задание 1
Найдите корень уравнения $$4^{5x+2}=0,8cdot 5^{5x+2}$$
Ответ: -0,2
Задание 2
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,25
Задание 3
В тупоугольном треугольнике АВС известно, что АС=ВС=10, высота АН равна $$sqrt{51}$$. Найдите косинус угла АСВ.
Ответ: -0,7
Задание 4
Найдите значение выражения $$frac{5sin 61^{circ}}{sin 299^{circ}}$$
Ответ: -5
Задание 5
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Ответ: 72
Задание 6
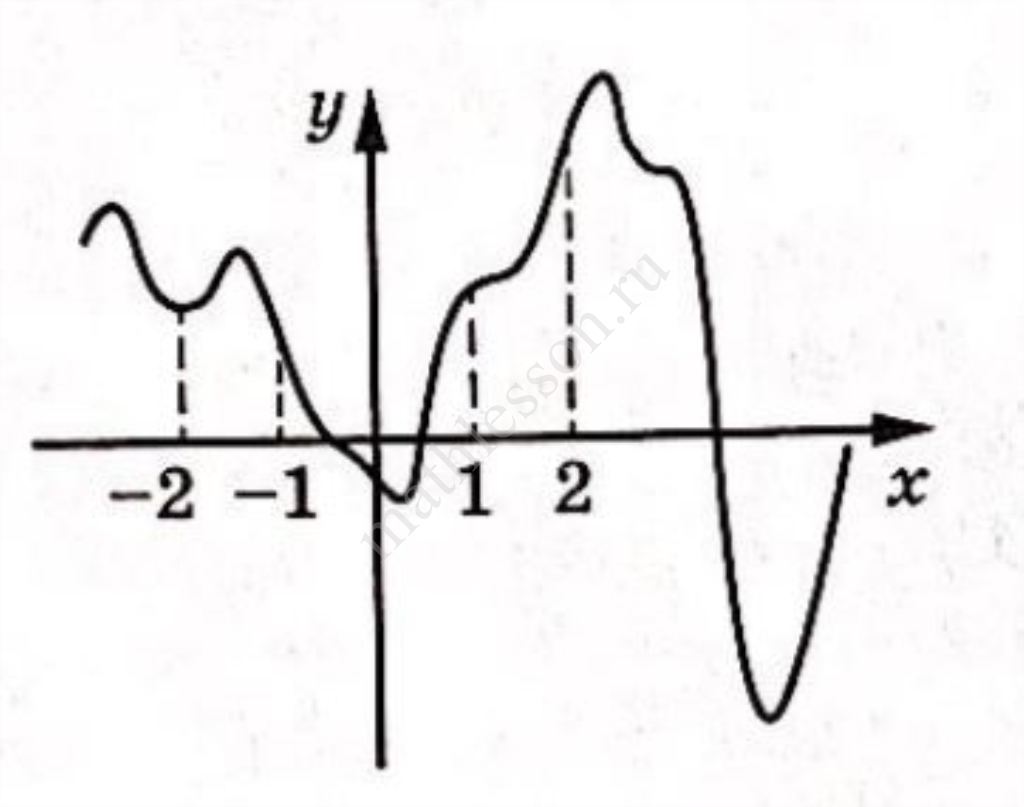
На рисунке изображён график y=f(x). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: -1
Задание 7
При температуре 0°C рельс имеет длину l0=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t_{0})=l_{0}(1+alpha cdot t^{circ})$$, где $$alpha=1,2cdot 10^{-5}$$(°C) — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.
Ответ: 50
Задание 8
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Ответ: 17,5
Задание 9
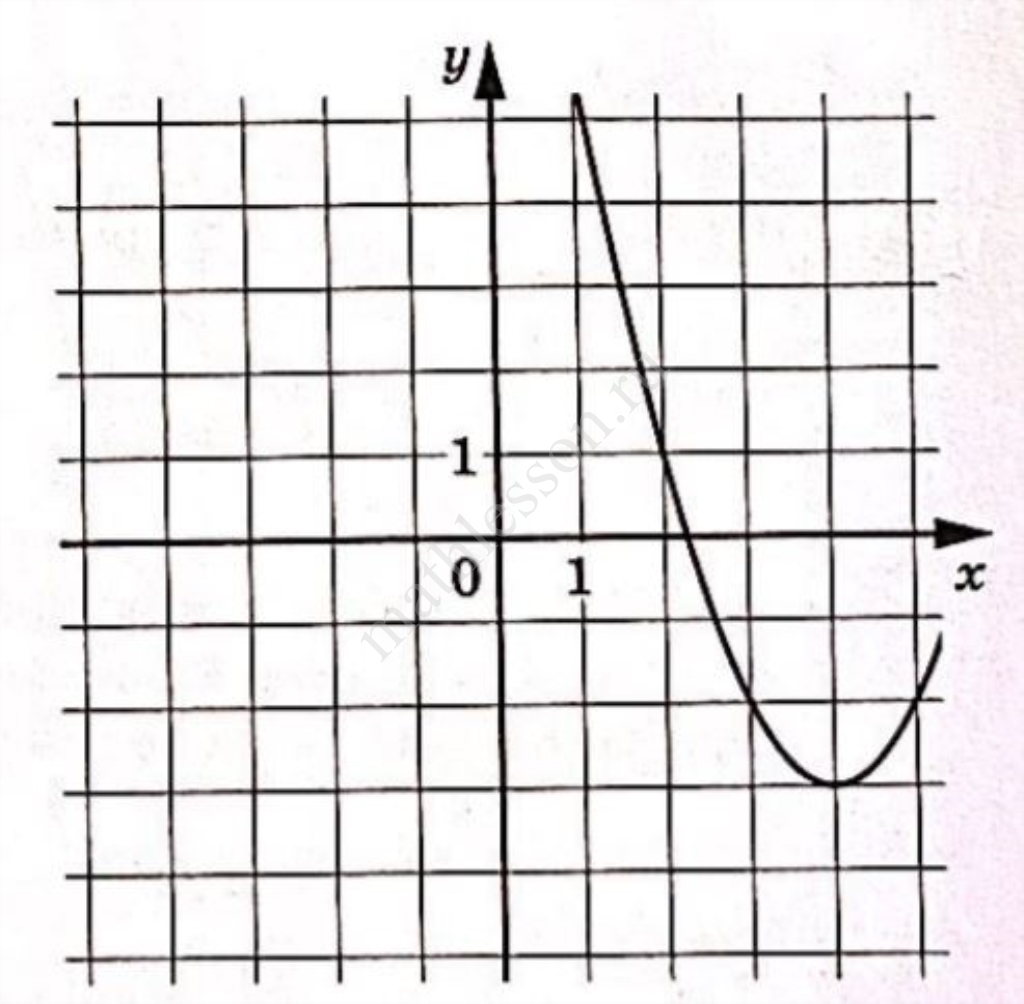
На рисунке изображён график функции $$f(x)=ax^{2}+bx+c$$, где числа a,b и с — целые. Найдите $$f(-5)$$.
Ответ: 72
Задание 10
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 30% этих стёкол, вторая — 70%. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 4 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,043
Задание 11
Найдите наименьшее значение функции $$y=frac{4}{3}xsqrt{x}-3x+9$$ на отрезке $$[0,25;30]$$.
Ответ: 6,75
Задание 12
а) Решите уравнение $$2sin^{3}(pi+x)=frac{1}{2}cos (x-frac{3pi}{2})$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi}{2};-frac{5pi}{2}]$$
Ответ: а) $$pi k;pm frac{pi}{6}+pi n, k,n in Z$$ б) $$-frac{19pi}{6};-3pi;-frac{17pi}{6}$$
Задание 13
В правильной треугольной пирамиде SABC сторона основания АВ равна 16, высота SH равна 10. Точка К — середина бокового ребра SA. Плоскость, параллельная плоскости АВС, проходит через точку К и пересекает рёбра SB и SC в точках Q и Р соответственно.
а) Докажите, что площадь четырёхугольника BCPQ составляет $$frac{3}{4}$$ треугольника SBC.
б) Найдите объём пирамиды KBCPQ.
Ответ: $$80sqrt{3}$$
Задание 14
Решите неравенство: $$(4^{x}-5cdot 2^{x})-20(4^{x}-5cdot 2^{x})leq 96$$
Ответ: $$(-infty;0];[2;3]$$
Задание 15
В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
— в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?
Ответ: 600 тыс. руб.
Задание 16
Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём АЕ=ED=CD, а прямые АС и BE перпендикулярны. Отрезки АС и BD пересекаются в точке Т.
а) Докажите, что прямая ЕС пересекает отрезок TD в его середине.
б) Найдите площадь треугольника АВТ, если BD=6, $$AE=sqrt{6}$$
Ответ: $$frac{8sqrt{}5}{3}$$
Задание 17
Найдите все значения а, при каждом из которых уравнение $$|x^{2}-a^{2}|=|x+a|cdot sqrt{x^{2}-4ax+5a}$$ имеет ровно один корень.
Ответ: $$-5;(0;1)$$
Задание 18
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?
Ответ: а)да б)нет в)97
👀 Просмотров: 1146
Инфо
Автор: И.В. Ященко
Предмет (категория): Профильный уровень. 36 вариантов заданий
Класс:
Читать онлайн: Да
Скачать бесплатно: Да
Формат книги: jpg / pdf
Размер книги/ГДЗ: 25,8 Мб
Год публикации (выпуска): 2022
Самые популярные статьи:
- ЕГЭ 2015. Ященко Математика. 36 вариантов.
- Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
- Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
- Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
- Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика
Вперёд >
Наверх
ПОДЕЛИТЬСЯ
Новый сборник Ященко И.В ЕГЭ 2022 года по математике профильный уровень 36 тренировочных вариантов с ответами и решением для подготовки к ЕГЭ.
В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2022 года; инструкция по выполнению экзаменационной работы; ответы ко всем заданиям; решения и критерии оценивания заданий 13-19.
Скачать бесплатно сборник Ященко в PDF
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Посмотрите также другие сборники Ященко:
Сборник ЕГЭ 2022 Ященко Семенов по математике профильный уровень варианты с ответами
Сборник ОГЭ 2022 Ященко 36 вариантов по математике 9 класс
Решение и ответы заданий Варианта №2 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.
Задание 1.
Найдите корень уравнения 92х+5 = 3,24·52х+5.
Задание 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задание 3.
В тупоугольном треугольнике ABC известно, что AC = BC, высота AH равна 3, СН = √7. Найдите синус угла ACB.
Задание 4.
Найдите значение выражения .
Задание 5.
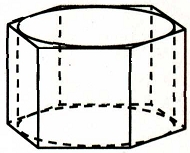
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.
Задание 6.
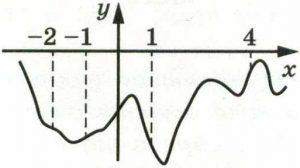
На рисунке изображён график функции 𝑦 = 𝑓(𝑥). На оси абсцисс отмечены точки −2, –1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Задание 7.
При температуре 0°С рельс имеет длину 𝑙0 = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 𝑙(𝑡°) = 𝑙0(1 + 𝛼∙𝑡°), где 𝛼 = 1,2∙10−5(°С )−1 – коэффициент теплового расширения, 𝑡° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.
Задание 8.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно в А со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Задание 9.
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−9).
Задание 10.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.
Задание 12.
а) Решите уравнение 2cos3(x – π) = sin( + x).
б) Найдите все корни уравнения, принадлежащие отрезку .
Задание 13.
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет площади треугольника SCD.
б) Найдите объем пирамиды ACDKP.
Задание 14.
Решите неравенство (25х – 4·5х)2 + 8·5х < 2·25x + 15.
Задание 15.
В июле 2023 года планируется взять кредит на 10 лет. Условия его возврата таковы:
– каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
– каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей?
Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC = CD = DE, а AC⊥BE. Точка K – пересечение прямых BE и AD.
а) Докажите, что прямая EC делит отрезок KD пополам.
б) Найдите площадь треугольника ABK, если AD = 4, DC = √3.
Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение
|x2 – a2| = |x + a|·
имеет ровно два различных корня.
Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.