Задание 1
В университетскую библиотеку привезли новые учебники для четырёх курсов, по 360 штук для каждого курса. В книжном шкафу 7 полок, на каждой полке помещается 20 учебников. Какое наименьшее количество шкафов потребуется, чтобы в них разместить все новые учебники?
Ответ: 11
Задание 2
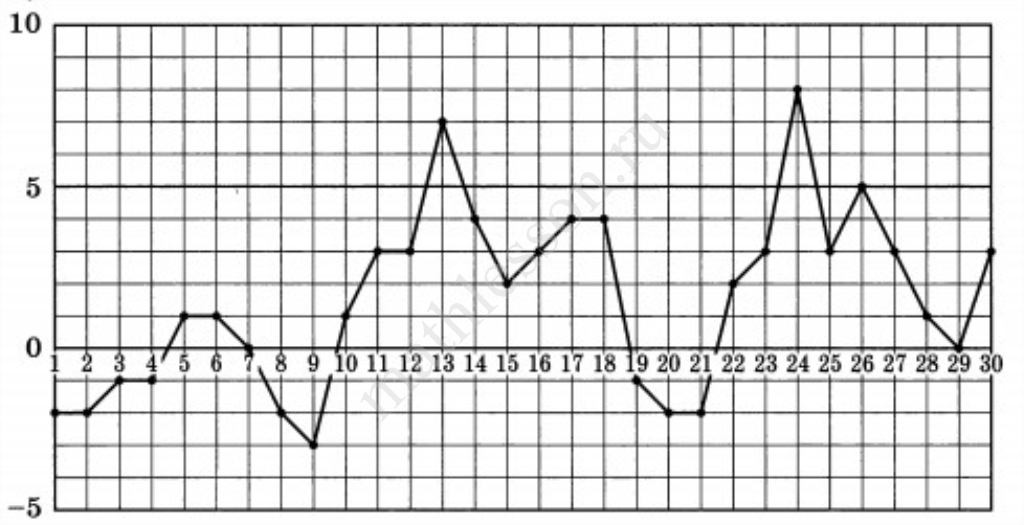
На рисунке жирными точками показана средняя температура воздуха в Мурманске во все дни апреля 2018 года. По горизонтали указываются числа месяца, по вертикали — средняя температура в градусах Цельсия. Для наглядности точки на рисунке соединены линией.
Определите, сколько дней в апреле 2018 года средняя температура в Мурманске была меньше 1.5 градуса Цельсия.
Ответ: 15
Задание 3
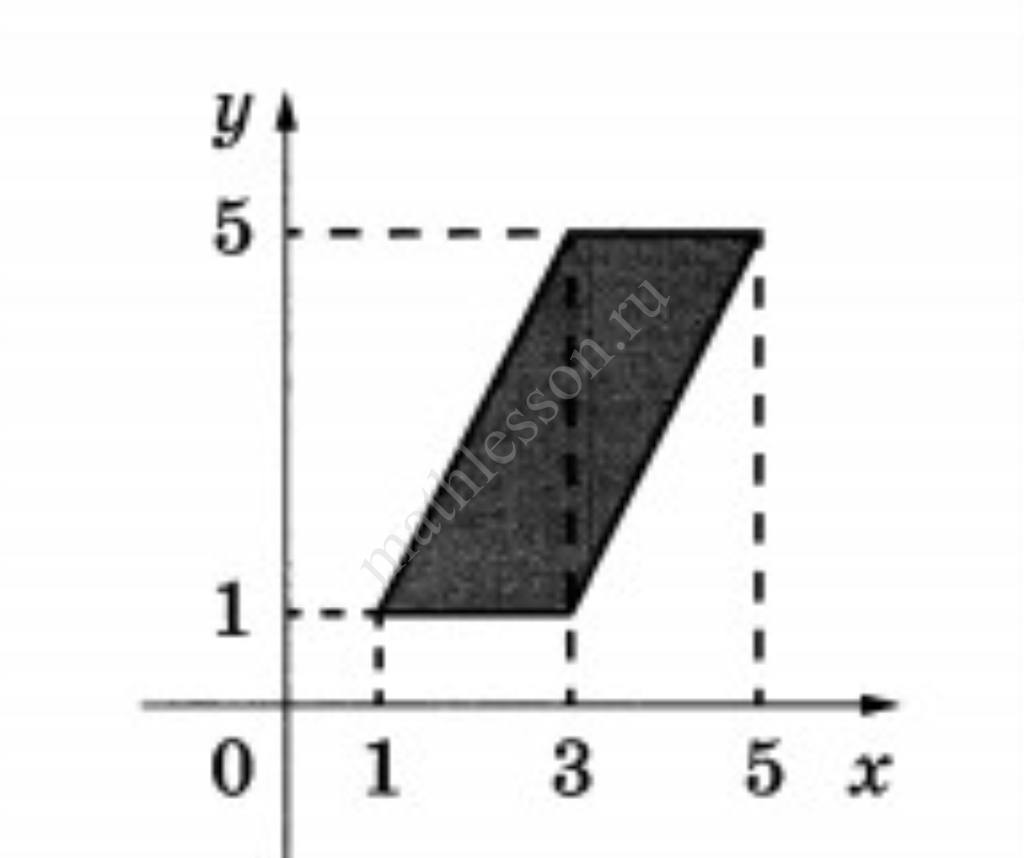
Найдите площадь параллелограмма, изображённого на рисунке.
Ответ: 8
Задание 4
Из ящика, в котором лежат фломастеры, не глядя достали два фломастера. Найдите вероятность того, что эти фломастеры оказались одного цвета, если известно, что в ящике 12 синих и 13 красных фломастеров.
Ответ: 0,48
Задание 5
Найдите корень уравнения $$8^{x-3}={16}^{2x}$$
Ответ: -1,8
Задание 6
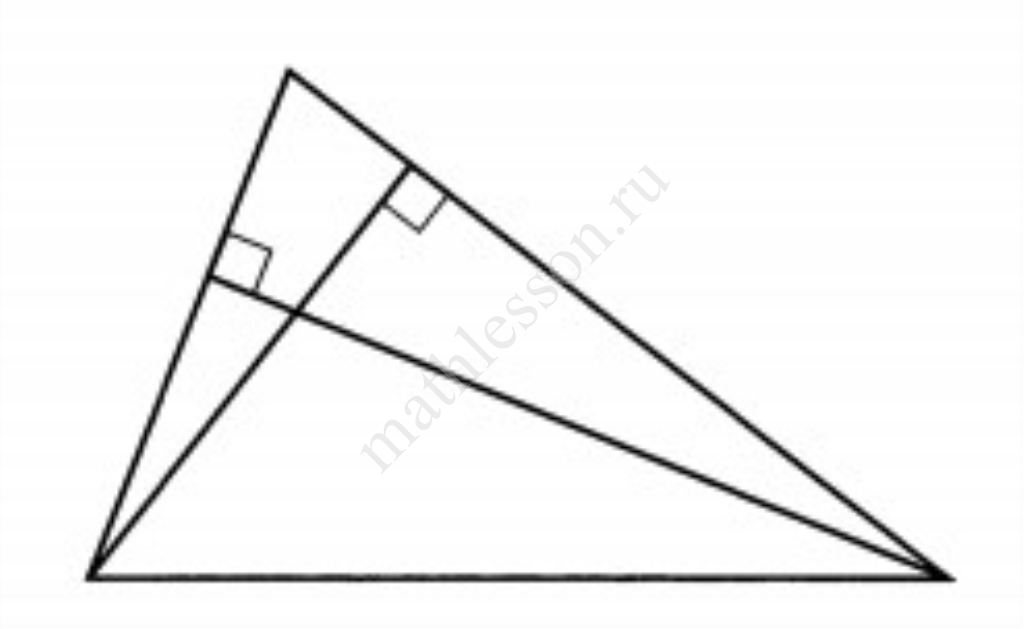
Два угла треугольника равны 68$${}^circ$$ и 35$${}^circ$$. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Ответ: 103
Задание 7
На рисунке изображён график функции $$y= f(x).$$ На оси абсцисс отмечено восемь точек: $$x_1, x_2, … x_8.$$ Найдите количество точек, в которых производная функции $$f(x)$$ положительна.
Ответ: 7
Задание 8
Шар вписан в цилиндр. Площадь поверхности шара равна 26. Найдите площадь полной поверхности цилиндра.
Ответ: 39
Задание 9
Найдите значение выражения $$frac{10cos105{}^circ }{sin 15{}^circ cdot cos 60{}^circ }$$
Ответ: -20
Задание 10
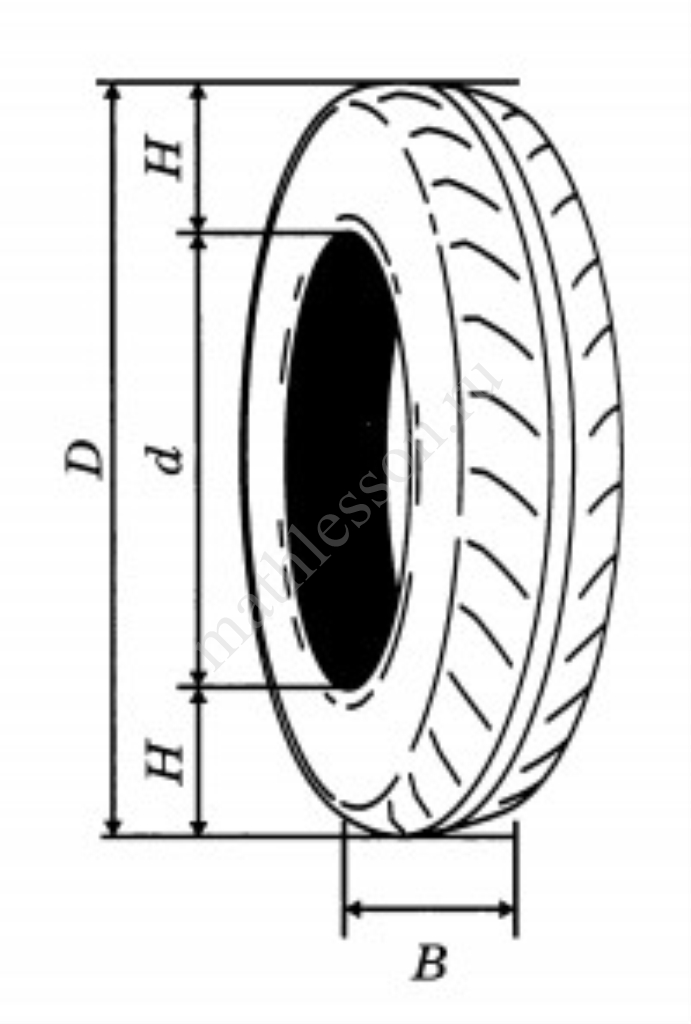
На автомобильной шине с помощью специальной маркировки указаны её размеры. Например, 265/60R18. Первое число означает ширину шины В в миллиметрах (см. рис.). Второе число означает отношение высоты профиля шины Н к ширине шины в процентах. Буква означает конструкцию шины (R — радиальный тип), а последнее число означает диаметр обода колеса d в дюймах.
На автомобиль «Лада-Калина» завод устанавливает шины с маркировкой 185/60R14. Найдите диаметр колеса D этого автомобиля. В одном дюйме 25,4 мм. Ответ дайте в сантиметрах с округлением до целого.
Ответ: 58
Задание 11
Автомобиль выехал с постоянной скоростью 72 км/ч из города А в город В, расстояние между которыми равно 246 км. Одновременно с ним из города С в город В, расстояние между которыми равно 221 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 35 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.
Ответ: 78
Задание 12
Найдите наименьшее значение функции $$y = 5x-ln(5x) + 12$$ на отрезке $$[frac{1}{10};frac{1}{2}]$$
Ответ: 13
Задание 13
а) Решите уравнение $$sin x+sqrt{2}{sin left(frac{pi }{4}-2xright) }=cos2x$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[4pi ; frac{11pi }{2}]$$
Ответ: а) $$pi k, pm frac{pi }{3}+2pi k$$; б) $$4pi , 5pi , frac{13pi }{3}$$
Задание 14
Точки А, В и С лежат на окружности основания конуса с вершиной S, причём А и С диаметрально противоположны. Точка М — середина ВС.
а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если $$AB= 4, BC= 6 и SC = 4sqrt{2}.$$
Ответ: $$arcsinsqrt{frac{19}{46}}$$
Задание 15
Решите неравенство $$20{log}^2_4(cos x) + 4{log}_2(cos x)le 1.$$
Ответ: $$[-frac{pi }{3}+2pi k; frac{pi }{3}+2pi k], kin Z$$
Задание 16
На гипотенузе АВ и катетах ВС и АС прямоугольного треугольника АВС отмечены точки М, N и К соответственно, причём прямая NK параллельна прямой АВ и $$BM=BN =frac{1}{2}KN.$$ Точка Р -середина отрезка KN.
а) Докажите, что четырёхугольник ВСРМ — равнобедренная трапеция.
б) Найдите площадь треугольника АВС, если $$BM = 2$$ и $$angle BCM = 30{}^circ .$$
Ответ: $$8sqrt{3}$$
Задание 17
Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн рублей.
Ответ: 5000000 рублей
Задание 18
Найдите все значения а, при каждом из которых система уравнений $$left{ begin{array}{c} left(ay-ax+2right)left(y-x+3aright)=0 \ left|xyright|=a end{array} right.$$ имеет ровно восемь решений.
Ответ: $$frac{4}{9}<a<sqrt{frac{2}{3}}; sqrt{frac{2}{3}}<a<1$$
Задание 19
Известно, что в кошельке лежало n монет, каждая из которых могла иметь достоинство 2, 5 или 10 рублей. Таня сделала все свои покупки, расплатившись за каждую покупку отдельно без сдачи только этими монетами, потратив при этом все монеты из кошелька.
а) Могли ли все её покупки состоять из блокнота за 64 рубля и ручки за 31 рубль, если $$n = 16?$$
б) Могли ли все её покупки состоять из стакана компота за 15 рублей, сырка за 20 рублей и булочки за 25 рублей, если $$n = 26?$$
в) Какое наименьшее количество пятирублёвых монет могло быть в кошельке, если Таня купила только альбом за 96 рублей и $$n = 19?$$
Ответ: а) да; б) нет; в) 6
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку ![displaystyle [pi; frac{3pi}{2}].](https://l.wordpress.com/latex.php?latex=%5Cdisplaystyle%20%5B%5Cpi%3B%20%5Cfrac%7B3%5Cpi%7D%7B2%7D%5D.&bg=FFFFFF&fg=000000&s=1 "displaystyle [pi; frac{3pi}{2}].")
Решение:
а)
Сделаем замену переменной 
Применим формулу приведения:
Получим:
ОДЗ: 
Поделим обе части уравнения на cos 
.
Решим систему с помощью тригонометрического круга
Решение системы:
или 
Вернёмся к переменной 
или 
б) Найдём корни на отрезке ![displaystyle [pi; frac{3 pi}{2}]](https://l.wordpress.com/latex.php?latex=%5Cdisplaystyle%20%5B%5Cpi%3B%20%5Cfrac%7B3%20%5Cpi%7D%7B2%7D%5D&bg=FFFFFF&fg=000000&s=1 "displaystyle [pi; frac{3 pi}{2}]")
с помощью двоинчных неравенств.
1) Серия 
![displaystyle 2 frac{5}{6}leq n leq 4 frac{1}{3}; [math]n= 3](https://l.wordpress.com/latex.php?latex=%5Cdisplaystyle%202%20%5Cfrac%7B5%7D%7B6%7D%5Cleq%20n%20%5Cleq%204%20%5Cfrac%7B1%7D%7B3%7D%3B%20%5Bmath%5Dn%3D%203&bg=FFFFFF&fg=000000&s=1 "displaystyle 2 frac{5}{6}leq n leq 4 frac{1}{3}; [math]n= 3")
или 
Тогда 
или 
2) Серия 
или 
или 
Ответ: а) 
б) 
Обратите внимание на область допустимых значений уравнения. Поскольку в уравнении содержится функция tg x, появляется условие cos x не равен нулю.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи из сборников Ященко, 2021 год, Вариант 22» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Mat-EGE.ru >> Все варианты базового ЕГЭ >> Вариант № 22
Поделиться Вконтакте
ПОДПИСАТЬСЯ (YOUTUBE)
№ задания:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| 3267 | При производстве в среднем на каждые 1500 насосов приходится 36 неисправных. Найдите вероятность тог, что случайно выбранный насос окажется неисправным Решение |
При производстве в среднем на каждые 1500 насосов приходится 36 неисправных ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 2 | |
| 3266 | Цилиндр и конус имеют общие основания и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 27sqrt2. Найдите площадь боковой поверхности конусаРешение |
Цилиндр и конус имеют общие основания и высоту ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 5 | |
| 3265 | В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер достанут третьим по счету?Решение |
В ящике 3 красных и 3 синих фломастера ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 10 | |
| 3264 | Найдите точку максимума функции y=x^3+18x^2+81x+23Решение  График |
Найдите точку максимума функции y=x3 + 18×2 +81x +23 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 11 | |
| 2624 | Плиточник должен уложить 120 м2 плитки. Если он будет укладывать на 8 м2 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?Решение |
Плиточник должен уложить 120 квадратных метров плитки ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 8 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 11 | |
| 2623 | Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E. а) Докажите, что /_EOC=/_ECO. б) Найдите площадь треугольника ACE, если радиус описанной около треугольника ABC окружности равен 6sqrt3, /_ABC=60^@ Решение |
Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 16 # Задача-аналог 2881 | |
| 2622 | а) Решите уравнение 2sin^2(x)-3sqrt(3)sin(pi/2+x)-5=0 б) Укажите корни этого уравнения, принадлежащие отрезку [-(5pi)/2; -pi].Решение График |
Решите уравнение 2sin квадрат x -3 корня из 3 sin(pi/2+x) -5 =0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 12 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 13 |
|
| 2621 | В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 5. На ребре SС отмечена точка K, причём SK:KC=1:3. Плоскость alpha содержит точку K и параллельна плоскости SAD. а) Докажите, что сечение пирамиды SABCD плоскостью alpha — трапеция. б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD плоскостью alphaРешение |
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 14 | |
| 2620 | Решите неравенство log_{2}(18-9x) — log_{2}(x+2) > log_{2}(x^2-6x+8)Решение График |
Решите неравенство log_{2}(18-9x) — log_{2}(x+2) > log_{2}(x^2 -6x+8) ! 36 вариантов ФИПИ Ященко 2022 Вариант 22 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 12 Задание 15 | |
Напиши мне, решений каких вариантов не хватает на сайте?
Например: «Сборник Лысенко ЕГЭ 2023 профиль 40 вариантов», «Варианты Ларина ЕГЭ 2023 профиль», «Варианты СтатГрад ЕГЭ 2023 профиль» и т.п.
Варианты СтатГрад ЕГЭ 2023 (профильный уровень)
Варианты сборника И.В. Ященко ЕГЭ 2023 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2022 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2021 (профильный уровень), 36 вариантов.
Варианты сборника Ф.Ф. Лысенко ЕГЭ 2021 (профильный уровень), 40 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2020 (профильный уровень), 36 вариантов.
- 04.11.2020
Сборник ответов для пособия ОГЭ 2021, 36 типовых вариантов по математике профильного уровня, под редакцией Ященко И.В., для выпускников 9 классов
- Тренировочные варианты ОГЭ 2021 по математике
- Работы СтатГрад 2020-2021
Выбирайте вариант и смотрите ответы. Вы можете скачать или сохранить их совершенно бесплатно.
Выберите свой номер варианта теста:
1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36
Вариант 1
Видеоразбор варианта №1
1) 56,4
2) 8070
3) 62,5
4) 9813
5) 13
6) -2,8
7) 2
8
9) -2,5
10) 0,42
11) 213
12) 3
13) 3
14) 1031
15) 174
16) 5
17) 86
18) 12
19) 12
20) 2; 6
21) 16 км/ч
22) [ — 6,25; — 2,25],[0; + ∞)
23) 18
25) 3:10
Вариант 2
1) 60,6
2) 9910
3) 67,5
4) 11 445
5) 15
6) -7
7) 2
25
9) -0,5
10) 0,65
11) 123
12) 6
13) 4
14) 764
15) 216
16) 32
17) 54
18) 25
19) 23
20) -2; -5
21) 14 км/ч
22) [ — 4; — 1],[0; + ∞)
23) 15
25) 11:15
Вариант 3
Видеоразбор варианта №3
1) 61254
2) 160
3) 38
4) 225
5) 15,4
6) 1,25
7) 1
8
9) -4
10) 0,8
11) 231
12) 0,0003
13) 4
14) -53,7
15) 8
16) 23
17) 42
18) 4
19) 1
20) -4; -3; 2
21) 35 %
22) -4; 0; 4
23) 7
25) 20,8
Вариант 4
1) 24536
2) 120
3) 34
4) 12,5
5) 9,4
6) 1,65
7) 4
5
9) 10
10) 0,64
11) 123
12) 0,007
13) 3
14) -21,8
15) 12
16) 15
17) 65
18) 4
19) 3
20) -3; -1; 2
21) 55 %
22) -6,25; 0; 6,25
23) 8
25) 7,2
Вариант 5
Видео разбор 5 варианта ОГЭ 2021
1) 1243
2) 51
3) 39
4) 153
5) 148
6) -19,2
7) 1
240
9) -5
10) 0,45
11) 312
12) 8
13) 2
14) 740
15) 7
16) 147
17) 96
18) 4
19) 1
20) ( — 4 — √{10} ; — 4 + √{10} )
21) 173 км
22) -4; 5
23) 17
25) 924
Вариант 6
1) 1432
2) 25
3) 105
4) 17
5) 100
6) -18,2
7) 2
216
9) -6
10) 0,35
11) 231
12) 3
13) 3
14) 1230
15) 11
16) 118
17) 44
18) 8
19) 2
20) ( — ∞ ; — 2 — √5 )(√5 — 2; + ∞)
21) 218 км
22) -2,25; 4
23) 5
25) 1120
Вариант 7
Видеоразбор 7 варианта
1) 8
2) 14
3) 3,2
4) 120
5) 135-145
6) 20
7) 2
81
9) 5
10) 0,12
11) 231
12) 48
13) 2
14) 48
15) 0,7
16) 74
17) 51
18) 7
19) 13
20) -3; 1
21) 17 км/ч
22) -1; о
23) 8
25) 14,4
Вариант 8
1) 7
2) 7
3) 1,6
4) 13
5) 8,7-8,9
6) 12
7) 4
256
9) -5
10) 0,09
11) 312
12) 320
13) 2
14) 36
15) 0,7
16) 36
17) 60
18) 5
19) 23
20) -4; 1
21) 21 км/ч
22) -0,25; 0
23) 6
25) 13,5
Вариант 9
1) 195
2) 6
3) 65,24
4) 15,2
5) 2,3
6) 3,9
7) 4
6
9) -6,2
10) 0,375
11) 231
12) 24
13) 4
14) 12
15) 108
16) 40
17) 4,5
18) 0,6
19) 1
20) (7;7 + √{11} )
21) 14 л/мин.
22) -2; 2
23) 6
25) 28,8
Вариант 10
1) 185
2) 1
3) 60,3
4) 13,3
5) 2,2
6) 5,75
7) 3
6
9) -16
10) 0,24
11) 312
12) 0,8
13) 3
14) 10
15) 139
16) 57
17) 98
18) 3
19) 1
20) (5;5 + √{11} )
21) 10 л/мин.
22) 3; 4
23) 18
25) 37,1
Вариант 11
1) 3412
2) 64
3) 420
4) 310,8
5) 14
6) 8
7) 3
49
9) -3,5
10) 0,8
11) 321
12) 15
13) 3
14) 20
15) 13
16) 53
17) 91
18) 10
19) 13
20) -7; -2; 2
21) 21 т
22) -1; 0; 1
23) 10
25) 7,2
Вариант 12
1) 3142
2) 8
3) 594
4) 155,4
5) 0,7
6) 4,4
7) 4
125
9) 0,2
10) 0,875
11) 312
12) 3
13) 1
14) 30
15) 34
16) 79
17) 46
18) 9
19) 23
20) -4; -1; 1
21) 36 т
22) -4; 0; 1
23) 32
25) 6,5
Вариант 13
1) 46531
2) 120
3) 19
4) 3,36
5) 25
6) 44,9
7) 3
3,2
9) -10,25
10) 0,16
11) 312
12) 578
13) 3
14) 3
15) 24
16) 637
17) 18
18) 5
19) 1
20) (3; 4); (3; -4)
21) 700 м
22) -9; 4
23) 52
25) 8; 4
Вариант 14
1) 76324
2) 160
3) 17
4) 8,96
5) 22
6) 29,5
7) 2
40,5
9) -2,7
10) 0,12
11) 213
12) 32
13) 2
14) 5
15) 43
16) 119
17) 7
18) 10
19) 3
20) (2; 4); (2; -4)
21) 650 м
22) -2,25; 12,25
23) 33
25) 37; 3
Вариант 15
1) 14532
2) 54
3) 20
4) 34
5) 202
6) 0,9
7) 3
64
9) 0,4
10) 0,375
11) 123
12) 4
13) 3
14) 57 960
15) 21
16) 103
17) 56
18) 6
19) 13
20) 15
21) 38 %
22) -1; 1; 1,25
23) 76
25) 24√{13;} 48√{13;} 72√{5;}
Вариант 16
1) 34125
2) 25
3) 132
4) 78
5) 127
6) 1,8
7) 1
343
9) -1,8
10) 0,15
11) 213
12) 0,7
13) 1
14) 110 900
15) 24
16) 97
17) 61
18) 3
19) 12
20) 6
21) 30 %
22) -4; 4; 5
23) 58
25) 3√{13;} 6√{13;} 9√{5;}
Вариант 17
1) 61,5
2) 10 580
3) 94,1
4) 11 819
5) 12
6) 1,03
7) 2
8
9) 3,5
10) 0,24
11) 312
12) 66
13) 4
14) 530
15) 0,8
16) 9
17) 133
18) 12,5
19) 2
20) 2 — √{2;} 2 + √2
21) 23 км/ч
22) 1; 4
23) 6,5
25) 42
Вариант 18
1) 58,5
2) 8800
3) 65
4) 10 613
5) 8
6) 3,95
7) 1
11
9) -1,5
10) 0,34
11) 213
12) 11
13) 2
14) 570
15) 0,375
16) 13
17) 71
18) 7,5
19) 3
20) 4 — √{7;} 4 + √7
21) 17 км/ч
22) 0,5; 4
23) 15
25) 96
Вариант 19
1) 10
2) 23
3) 1,6
4) 100
5) 62-63
6) 1,25
7) 2
64
9) -12
10) 0,2
11) 312
12) 17
13) 1
14) -16
15) 17,5
16) 36,5
17) 138
18) 45,5
19) 2
20) (-3; 5)
21) 15 %
22) 4
23) 17√6
25) 3√2
Вариант 20
1) 9
2) 10
3) 3,2
4) 60
5) 9-9,3
6) 1,5
7) 3
81
9) -9
10) 0,04
11) 213
12) 32
13) 4
14) -30,9
15) 27,5
16) 57,5
17) 65
18) 38,5
19) 2
20) (-1; 4)
21) 12 %
22) 4
23) 25√3
25) frac{{38√3 }}{3}
Вариант 21
1) 275
2) 7,25
3) 77,52
4) 17,8
5) 2,3
6) -3
7) 4
8
9) -3
10) 0,3
11) 321
12) 3,2
13) 1
14) 1175
15) 53
16) 24
17) 20
18) 4
19) 13
20) (-1; 8); (1;
21) 84 км/ч
22) 0,5
23) 20,16
25) √{30}
Вариант 22
1) 225
2) 4,75
3) 66,44
4) 7,6
5) 1Д
6) -2
7) 1
0,2
9) -2
10) 0,74
11) 213
12) 85
13) 2
14) 642
15) 97
16) 12
17) 32
18) 6
19) 13
20) (2; 10); (0,75; 0)
21) 80 км/ч
22) 1
23) frac{{240}}{{13}}
25) 2√2
Вариант 23
1) 74632
2) 22,4
3) 4
4) 32
5) 55
6) 0,7
7) 4
25
9) -4
10) 0,7
11) 213
12) 4
13) 4
14) 700
15) 18
16) 46
17) 109
18) 7,5
19) 2
20) -2
21) 420 кг
22) 3; 3,5
23) 16
25) 112
Вариант 24
1) 62471
2) 240
3) 5
4) 6,24
5) 26,1
6) 1,2
7) 1
32
9) 2
10) 0,85
11) 231
12) 4
13) 3
14) 624
15) 24
16) 12
17) 91
18) 32
19) 3
20) -7
21) 44 кг
22) 3; 3,2
23) 4,8
25) 15
Вариант 25
1) 51432
2) 39
3) 17
4) 117
5) 116
6) -1,5
7) 1
6
9) 7
10) 0,3
11) 312
12) 72
13) 2
14) 45
15) 0,75
16) 95
17) 63
18) 1,5
19) 23
20) 40
21) 52,8 км/ч
22) -1; 4
23) 60°; 120°
25) 26
Вариант 26
1) 52314
2) 39
3) 117
4) 25
5) 116
6) -0,5
7) 2
10
9) -7
10) 0,32
11) 321
12) 150
13) 3
14) 68
15) 0,7
16) 50
17) 15
18) 2,5
19) 23
20) 2000
21) 76,5 км/ч
22) -1; 16
23) 60°; 120°
25) 17
Вариант 27
1) 3241
2) 32
3) 594
4) 1247,4
5) 1,4
6) -4
7) 3
0,5
9) -1
10) 0,15
11) 321
12) 3
13) 2
14) 40
15) 42
16) 73
17) 5
18) 9
19) 3
20) [1; 2]
21) 13%
22) 0; 1
23) 9
25) 6√{13}
Вариант 28
1) 4213
2) 16
3) 840
4) 623,7
5) 17
6) -24
7) 2
0,2
9) -0,4
10) 0,16
11) 132
12) 4
13) 1
14) 15
15) 44
16) 114
17) 9
18) 12
19) 2
20) ( — ∞ ; — 2] cup [frac{2}{7}; + ∞)
21) 16%
22) 2; 3
23) 15
25) √{751}
Вариант 29
1) 65,4
2) 11 470
3) 72,5
4) 13 204
5) 10
6) 78
7) 2
144
9) 2,5
10) 0,35
11) 231
12) 19
13) 4
14) 520
15) 43
16) 18
17) 21
18) 5
19) 2
20) -5
21) 14 км/ч
22) -6,75
23) 11
25) 78
Вариант 30
1) 60,6
2) 9890
3) 73
4) 11 461
5) 9
6) 84
7) 3
36
9) 1,5
10) 0,4
11) 123
12) 6
13) 2
14) 580
15) 27
16) 18
17) 8
18) 7
19) 2
20) -3
21) 15 км/ч
22) -1
23) 13
25) 300
Вариант 31
1) 9
2) 13
3) 3,8
4) 75-76
5) 1,6-1,7
6) -0,14
7) 3
45
9) -0,7
10) 0,05
11) 123
12) 29
13) 4
14) 8
15) 0,125
16) 8
17) 18
18) 4
19) 1
20) (-2; 6); (2; -6); (-6; 2); (6; -2)
21) 65 вопросов
22) -8;1/36
23) 40
25) 22
Вариант 32
1) 8
2) 14
3) 1,9
4) 80
5) 12,4-12,8
6) -0,55
7) 3
28
9) -0,6
10) 0,2
11) 123
12) 37
13) 1
14) 9
15) -0,2
16) 4
17) 13
18) 2
19) 3
20) (-1; 8); (1; -8); (-8; 1); (8; -1)
21) 57 вопросов
22) 0;1/4
23) 29
25) 9,6
Вариант 33
1) 53412
2) 120
3) 20
4) 10,08
5) 21
6) 1,3
7) 2
25
9) -0,8
10) 0,98
11) 123
12) 0,2
13) 1
14) 6
15) 1,6
16) 52
17) 289
18) 4
19) 23
20) -1;1/4
21) 14 км/ч
22) 0; 0,25
23) 36
25) 32
Вариант 34
1) 74132
2) 440
3) 50
4) 24,96
5) 120
6) 3,25
7) 3
15
9) -3
10) 0,95
11) 312
12) 0,5
13) 2
14) 2
15) 0,4
16) 13
17) 441
18) 1
19) 12
20) 2;13/4
21) 18 км/ч
22) 0; 4
23) 15
25) 56
Вариант 35
1) 4312
2) 105
3) 44
4) 75
5) 90
6) 0,47
7) 1
12,5
9) -0,8
10) 0,45
11) 132
12) 1260
13) 2
14) 49 380
15) 90
16) 41
17) 8
18) 5,5
19) 2
20) (8; -2)
21) 12 дет./ч
22) -1; 1
23) 7
25) 24
Вариант 36
1) 2341
2) 112
3) 60
4) 100
5) 96
6) 2,75
7) 3
1,8
9) -од
10) 0,35
11) 123
12) 850
13) 3
14) 65 030
15) 20
16) 11
17) 5
18) 3,5
19) 3
20) (-4; 13)
21) 27 дет./ч
22) -1; 1
23) 8
25) 13,5