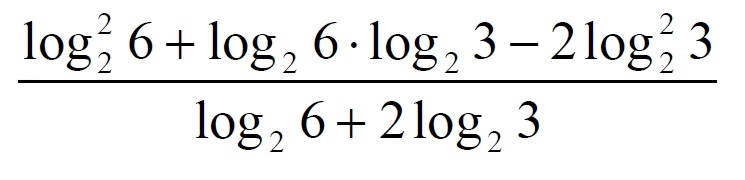Решение варианта 314 егэ ларин - Помощь в подготовке к экзаменам и поступлению

Задание 1

Поезд Иркутск‐Казань отправляется в 01:07 15 декабря (время иркутское), а прибывает в 15:52 17 декабря (время казанское). Сколько часов поезд находится в пути, учитывая, что смещение времени в Иркутске относительно Казани составляет +5 часов?

Ответ: 67,75

Задание 2

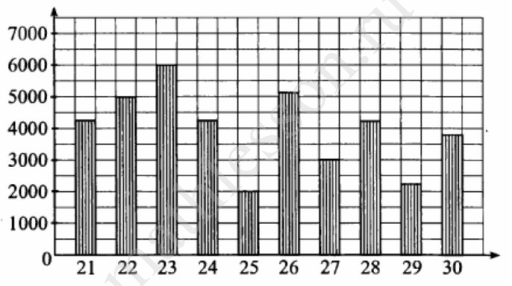
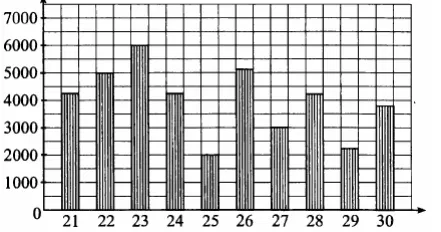
На диаграмме показано количество посетителей сайта любителей кошек во все дни с 21 по 30 мая 2009 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей превышает наименьшее количество посетителей за день (в указанный период)

Ответ: 3

Задание 3

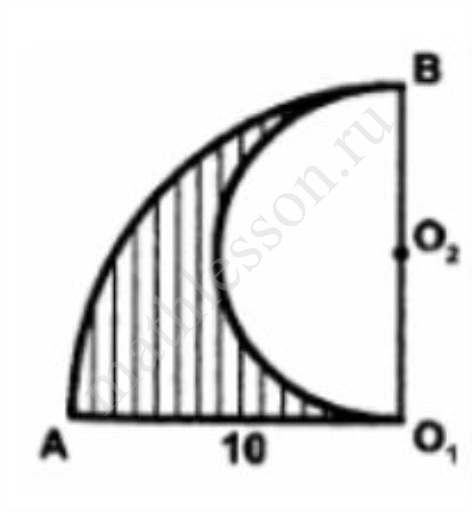
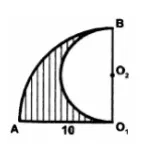
Найдите площадь S заштрихованной фигуры, изображенной на рисунке, если АО₁=10. В ответе укажите $$frac{S}{pi}$$.

Ответ: 12,5

Задание 4

Магазин покупает сливочное масло у двух молокозаводов. 40% масла первого и 20% масла второго молокозавода имеет жирность 80%. Всего жирность 80% имеет 35% закупленного масла. Найдите вероятность того, что масло, купленное в магазине, произведено первым молокозаводом.

Ответ: 0,75

Задание 5

Решите уравнение $$ln(frac{pi^{x}}{e^{x}}+2x-10)=x(ln pi-1)$$. Если корней больше одного, то в ответе запишите их сумму.

Ответ: 5

Задание 6

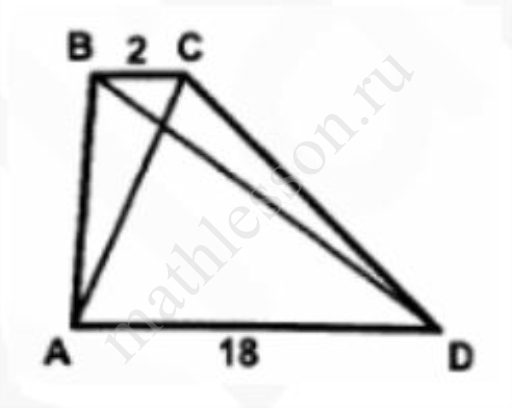
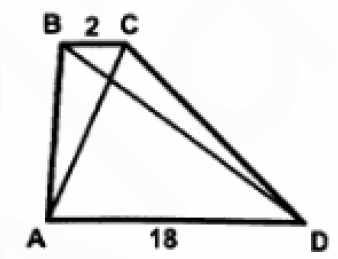
Найдите площадь трапеции, изображенной на рисунке, если АС=7, BD=15

Ответ: 42

Задание 7

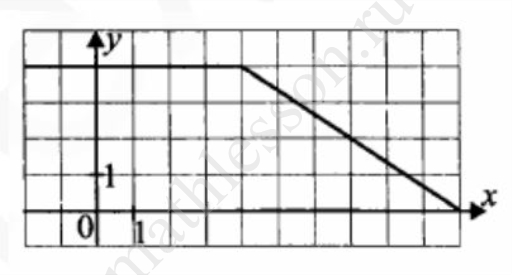
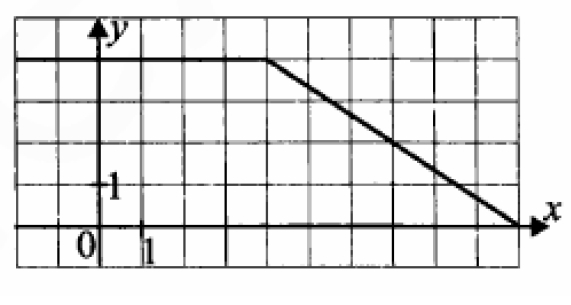
На рисунке изображен график функции $$y=f(x)$$. Пользуясь графиком, вычислите $$F(10)-F(2)$$, где $$F(x)$$ ‐ одна из первообразных функции $$y=f(x)$$.

Ответ: 20

Задание 8

В правильной треугольной пирамиде SABC сторона основания $$AB=8sqrt{3}$$ , а боковое ребро $$SA=sqrt{73}$$. Найдите расстояние от точки В до плоскости SAC.

Ответ: 7,2

Задание 9

Найдите значение выражения $$frac{log^{2}_{2}6+log_{2}6cdotlog_{2}3-2log^{2}_{2}3}{log_{2}6+2log_{2}3}$$

Ответ: 1

Задание 10

Опорные «башмаки» шагающего экскаватора, имеющего массу m=2520 т, представляют собой две пустотелые балки длиной $$l=36$$ м и S шириной метров каждая. Давление P, в кПа, оказываемое экскаватором на почву, определяется формулой $$P=frac{mg}{2lS}$$, где m‐масса экскаватора (в тоннах), $$l$$ — длина балок (в метрах), g = 10 м/с²‐ ускорение свободного падения. Определите наименьшую возможную ширину опорных балок, если известно, что давление P должно не превышать 280 кПа. Ответ выразите в метрах.

Ответ: 1,25

Задание 11

Отрезок арифметической прогрессии содержит 16 членов с номерами от 1 до 16. Сумма членов с четными номерами равна 42, а сумма членов с нечетными номерами равна 18. Найдите разность прогрессии.

Ответ: 3

Задание 12

Найдите наибольшее значение функции $$y=(1+x)log_{5}x$$ на отрезке [1;5]

Ответ: 6

Задание 13

а) Решите уравнение $$sqrt{ctg x}(sin^{2}x-frac{1}{4})=0$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};0]$$

Ответ: А)$$frac{pi}{6}+pi n, frac{pi}{2}+pi n, nin Z$$ Б)$$-frac{3pi}{2};-frac{5pi}{6};-frac{pi}{2}$$

Задание 14

Основание ABCD призмы ABCDA₁B₁C₁D₁ – трапеция с основаниями $$AB=2cdot CD$$

а) Докажите, что плоскость BA₁D₁ проходит через середину бокового ребра CC₁

б) Найдите угол между боковым ребром AA1 и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B , а BC=CD и $$AA_{1}=sqrt{6}CD$$

Ответ: $$30^{circ}$$

Задание 15

Решите неравенство $$frac{(4x-|x-6|)(log_{frac{1}{3}}(x+4)+1)}{2^{x^{2}}-2^{|x|}}geq 0$$

Ответ: $$(1;frac{6}{5}]$$

Задание 16

Точка I ‐ центр окружности, вписанной в треугольник ABC . Луч BI пересекает описанную около треугольника ABC окружность в точке N . Известно, что $$angle ABC=60^{circ}$$

а) Докажите, что N ‐ центр окружности, описанной около треугольника ABC N AIC

б) Найдите радиус окружности, описанной около треугольника , если известно, что IN=1.

Ответ: 1

Задание 17

Клиент положил в банк некоторую сумму денег. Через год, после начисления процентов, он добавил на свой счет сумму, составляющую 0,9 исходной, в результате чего остаток на счете стал равен 3,4 млн. рублей. А еще через год, после начисления процентов, остаток на его счете увеличился в 2,2 раза по сравнению с исходной суммой. Какую сумму клиент положил в банк первоначально, если в конце каждого года банк начислял один и тот же процент годовых?

Ответ: 1,7 млн. руб.

Задание 18

Найдите все значения параметра

$$aneq 0$$, такие что неравенство $$log^{2}_{2}(x^{2}+2ax+a^{2}-a+1)-log_{2}frac{a^{2}}{6}cdot log_{2}(x^{2}+2ax+a^{2}-a+1)leq 0$$

не имеет решений.

Ответ: $$(-3-sqrt{15};0)$$

Задание 19

На доске выписаны все натуральные числа от 1 до 2014 без пропусков и повторений: 1, 2, 3, …, 2013, 2014. С выписанными на доске числами проделывают следующие операции: выбирают какие‐либо два числа и записывают на доске модуль их разности, увеличенный на 1, а сами выбранные числа стирают. Так продолжают до тех пор, пока на доске не останется только одно число.

а) Какое наименьшее число может остаться на доске?

б) Какое наибольшее число может остаться на доске?

Ответ: А)2 Б)2014

Источник

Решение и ответы заданий № 1–12 варианта №314 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).

Задание 1.

Поезд Иркутск-Казань отправляется в 01:07 15 декабря (время иркутское), а прибывает в 15:52 17 декабря (время казанское). Сколько часов поезд находится в пути, учитывая, что смещение времени в Иркутске относительно Казани составляет +5 часов?

Задание 2.

На диаграмме показано количество посетителей сайта любителей кошек во все дни с 21 по 30 мая 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей превышает наименьшее количество посетителей за день (в указанный период).

Задание 3.

Найдите площадь S заштрихованной фигуры, изображённой на рисунке если, АО₁ = 10. В ответе укажите S/π.

Задание 4.

Задание 5.

Решите уравнение . Если корней больше одного, то в ответе запишите их сумму.

Задание 6.

Найдите площадь трапеции, изображенной на рисунке, если АС = 7, BD = 15.

Задание 7.

На рисунке изображен график функции y = f(x). Пользуясь графиком, вычислите F(10) − F(2), где F(x) ‐ одна из первообразных функции y = f(x).

Задание 8.

В правильной треугольной пирамиде SABC сторона основания AB = 8√3, а боковое ребро SA = √73. Найдите расстояние от точки В до плоскости SAC.

Задание 9.

Найдите значение выражения:

Задание 10.

Опорные «башмаки» шагающего экскаватора,

имеющего массу m = 2520 т, представляют собой две пустотелые балки длиной l = 36 м и шириной S метров каждая. Давление P, в кПа, оказываемое экскаватором на почву, определяется формулой:

где m ‐ масса экскаватора (в тоннах), l – длина балок (в метрах), g = 10 м/с² – ускорение свободного падения. Определите наименьшую возможную ширину опорных балок, если известно, что давление P должно не превышать 280 кПа. Ответ выразите в метрах.

Задание 11.

Задание 12.

Найдите наибольшее значение функции y = (1 + x)•log₅x на отрезке [1;5].

Источник варианта: alexlarin.net

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник


2299	Найдите площадь S заштрихованной фигуры, изображенной на рисунке, если A O_1=10. В ответе укажите S/pi Решение	Найдите площадь S заштрихованной фигуры, изображенной на рисунке ! Тренировочный вариант 314 от Ларина Задание 3 ЕГЭ

2298	Решите уравнение ln(pi^x/e^x+2x-10)=x(ln(pi)-1). Если корней больше одного, то в ответе запишите их сумму Решение График	Решите уравнение ln(pi^x /e^x +2x -10)= x(ln(pi) -1) ! Тренировочный вариант 314 от Ларина Задание 5 ЕГЭ

2297	Найдите площадь трапеции, изображенной на рисунке, если АС=7, BD=15 Решение	Найдите площадь трапеции, изображенной на рисунке, если АС=7, BD=15 ! Тренировочный вариант 314 от Ларина Задание 6 ЕГЭ

2296	В правильной треугольной пирамиде SABC сторона основания AB=8sqrt3, а боковое ребро SA=sqrt73. Найдите расстояние от точки В до плоскости SAC Решение	В правильной треугольной пирамиде SABC сторона основания AB = 8 корней из 3 , а боковое ребро SA= корень из 73 ! ларин егэ по математике 2020 профильный уровень Вариант 314 Задание 8

2295	Найдите значение выражения: ((log_{2}(6))^2+log_{2}(6)*log_{2}(3)-2(log_{2}(3))^2)/(log_{2}(6)+2log_{2}(3)) Решение График	Найдите значение выражения: ((log_{2}(6))^2 + log_{2}(6) * log_{2}(3) — 2(log_{2}(3)) ^2) / (log_{2}(6) + 2log_{2} (3)) ! ларин егэ по математике 2020 профильный уровень Вариант 314 Задание 9

2294	а) Решите уравнение sqrt(ctg(x))(sin^2(x) -1/4)=0 б) Укажите корни этого уравнения, принадлежащие отрезку [-(3pi)/2; 0]. Решение График	Решите уравнение sqrt(ctg x) (sin^2(x) -1/4) =0 ! Тренировочный вариант 314 от Ларина Задание 13 ЕГЭ

2044	Решите неравенство ((4x-abs(x-6))(log_{1/3}(x+4)+1))/(2^(x^2)-2^abs(x)) >= 0 Решение График	Решите неравенство ((4x- abs(x -6))(log_{1/3}(x+ 4)+ 1)) /(2^(x^2) — 2^abs(x)) >= 0 ! Тренировочный вариант 314 от Ларина Задание 15 # Тренировочный вариант 297 от Ларина Задание 15

Clear

Hide

Источник

На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023

Вариант №314 ЕГЭ Ларин Решение и ответы на задачи на официальном сайте источника онлайн.

Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/variant-314-ege-larin/

Ответы и решение задачи онлайн

Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.

Источник

2 новых тренировочных варианта №314 Алекса Ларина пробный ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии ФИПИ ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 23.02.2022 (23 февраля 2022 года)

Скачать тренировочный вариант №314

Скачать усложненную версию варианта

Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 25 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания.

Вариант Алекса Ларина №314 ОГЭ 2022 по математике 9 класс:

1)Вячеслав страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Вячеславу на начало третьего года страхования?

Правильный ответ: 2

2)Чему равен КБМ на начало третьего года страхования?

Правильный ответ: 1,4

3)Когда Вячеслав получил водительские права и впервые оформил полис, ему было 23 года. Чему равен КВС на начало 3‐го года страхования?

Правильный ответ: 1,63

4)В начале второго года страхования Вячеслав заплатил за полис 27 435 руб. Во сколько рублей обойдётся Вячеславу полис на третий год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?

Правильный ответ: 22820

5)Вячеслав въехал на участок дороги протяжённостью 3,3 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 80 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Вячеслав въехал на участок в 10:05:08, а покинул его в 10:07:20. Нарушил ли Вячеслав скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?

Правильный ответ: 10

10)В среднем на 100 карманных фонариков, поступивших в продажу, приходится четыре неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.

Правильный ответ: 0,96

11)Ниже представлен график некоторой функции. Установите соответствие между утверждениями для этой функции и промежутками, на которых верны эти утверждения. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.

Правильный ответ: 1432

14)Два приятеля положили в банк по 10 000 рублей каждый, причем первый положил деньги на вклад с ежеквартальным начислением 10%, а второй — с ежегодным начислением 45%. Через год приятели получили деньги вместе с причитающимися им процентами. На сколько рублей первый приятель получил больше второго приятеля?

Правильный ответ: 141

15)Найдите угол ABC   равнобедренной трапеции   ABCD , если диагональ   AC образует с основанием   AD   и боковой стороной     углы, равные и соответственно.

Правильный ответ: 120

19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) Если угол острый, то смежный с ним угол также является острым. 2) Диагонали квадрата взаимно перпендикулярны. 3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Правильный ответ: 23

23)Найдите площадь трапеции, диагонали которой равны 10 и 6, а средняя линия равна 4.

Правильный ответ: 45

25)Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 34 :13 , считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 39.

Правильный ответ: 141

Сложная версия варианта 314:

2)Сколько километров проедет Любовь Алексеевна от д. Калиновка до с. Малиновка, если поедет по шоссе через д. Рябиновка?

Ответ: 34

3)Найдите расстояние (в км) от пос. Ягодный до с. Малиновка по прямой.

Ответ: 40

4)Сколько минут Любовь Алексеевна затратит на дорогу из пос. Ягодный в с. Малиновка, если поедет сначала по шоссе, а затем свернёт в д. Калиновка на прямую тропинку, которая проходит мимо пруда?

Ответ: 186

5)В таблице (см. ниже) указана стоимость (в руб.) некоторых продуктов в четырёх магазинах, расположенных в с. Малиновка. Любови Алексеевне надо купить 0,5 кг сыра, 1 кг конфет, 500 г колбасы, 2 кг мяса, 3 кг персиков. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость (в рублях) данного набора продуктов в этом магазине.

Ответ: 2230

10)На книжной полке стоят 30 томов энциклопедии в некотором порядке. За одну операцию разрешается менять местами любые два соседних тома. За какое наименьшее число операций можно гарантированно выстроить все тома в правильном порядке (с первого по тридцатый слева направо) независимо от начального положения?

Ответ: 435

14)Ире надо подписать 880 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днём. Известно, что за первый день Ира подписала 10 открыток. Определите, сколько открыток было подписано за восьмой день, если вся работа была выполнена за 16 дней.

Ответ: 52

16)К окружности радиуса 7 проведены две касательные из одной точки, удалённой от центра на расстояние, равное 25. Найдите расстояние между точками касания.

Ответ: 13,44

17)В треугольнике ABC биссектриса угла A пересекает сторону в точке ; прямая, проведённая через точку параллельно BC D D AC , пересекает сторону AB в точке E ; прямая, проведённая через точку E параллельно BC , пересекает сторону AC в F . Найдите AE , если известно, что CF 3 .

Ответ: 3

19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) В тупоугольном треугольнике все углы тупые. 2) В любом параллелограмме диагонали точкой пересечения делятся пополам. 3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

Ответ: 23

24)Даны четыре прямые, которые образуют на плоскости ровно четыре треугольника. Докажите, что все четыре описанные окружности этих треугольников имеют ровно одну общую точку.