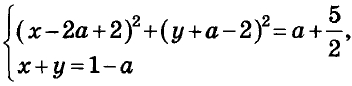Задание 1
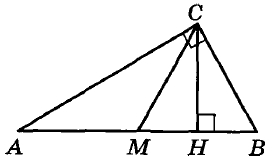
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна $$6sqrt{6}$$, $$BH=3$$ Найдите $$cos BAC$$.
Ответ: 0,2
Скрыть
Задание 2
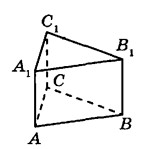
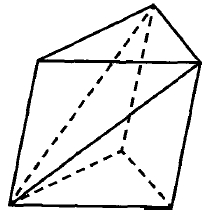
Найдите объём многогранника, вершинами которого являются точки $$B$$, $$C$$, $$A_1$$, $$C_1$$ правильной треугольной призмы $$ABCA_1B_1C_1$$ площадь основания которой равна 5, а боковое ребро равно 6.
Ответ: 10
Скрыть
Задание 3
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист 3. полетит третьим рейсом вертолёта.
Ответ: 0,2
Скрыть
Номер рейса в этой задаче не имеет значения. Важно, что за один рейс перевозятся 5 человек. То есть, вероятность попасть туристу З. на какой-либо рейс (в том числе и 3-й), равна:
$$P=frac{m}{n}=frac{5}{25}=frac{1}{5}=0,2$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,56
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{4})^{x+2}=256^{x}$$
Ответ: -0,4
Скрыть
Задание 6
Найдите значение выражения $$log_{2,5}6cdot log_{6} 0,4$$
Ответ: -1
Скрыть
Задание 7
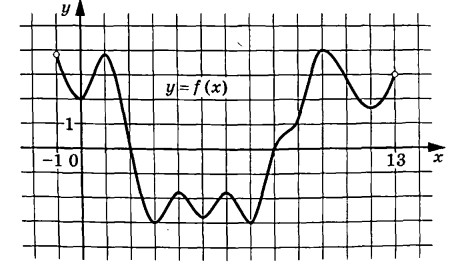
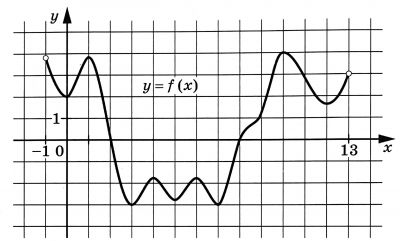
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-1; 13)$$. Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-2$$.
Ответ: 9
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$y=1,4+11t-5t^2$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 0,6
Скрыть
Задание 9
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси? Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 55
Скрыть
Задание 10
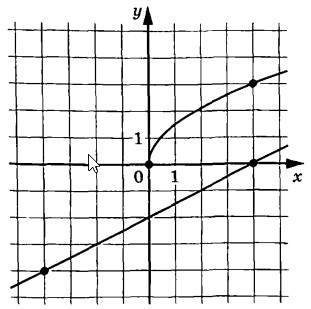
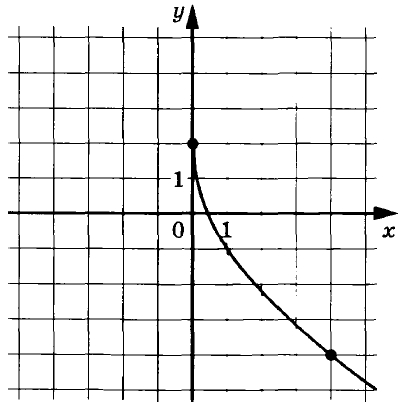
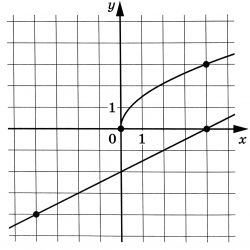
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точке $$A(x_0; y_0)$$. Найдите $$y_0$$.
Ответ: 6
Скрыть
Задание 11
Найдите точку максимума функции промежутку $$y=(2x-1)cos x-2sin x+9$$, принадлежащую промежутку $$(0;frac{pi}{2})$$
Ответ: 0,5
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(4x^{2})+3log_{0,5}(8x)=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0,15;1,5]$$
Ответ: а)$$0,25;sqrt[4]{8}$$ б)$$0,25$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$. Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что $$M$$ — середина $$SB$$.
б) Найдите расстояние между прямыми $$AC$$ и $$DM$$, если высота пирамиды равна $$6sqrt{3}$$.
Ответ: 3
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x+4}(8-3^{2+x^{2}})}{4^{x-1}-3}leq 0$$
Ответ: $$-4;(log_{4}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.
Ответ: 8 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной из вершины $$C$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что $$I$$ и $$J$$ лежат на отрезке $$EF$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=15$$, $$BC = 20$$.
Ответ: $$6sqrt{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{2}=|x|$$ и $$asqrt{2}+x=sqrt{2asqrt{2}-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$[sqrt{2};frac{3sqrt{6}}{sqrt{13}})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 68?
б) Может ли $$n$$ равняться 86?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)79
Скрыть
В треугольнике ABC известно, что AC=BC, высота AH=6√6, BH=3. Найдите cos∠BAC.
Найдите объём многогранника, вершинами которого являются вершины B,C,A₁,C₁ правильной треугольной призмы ABCA₁B₁C₁, площадь основания которой равна 5, а боковое ребро равно 6.
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Н. полетит вторым рейсом вертолёта.
Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 5. Какова вероятность, что для этого потребовалось два броска? Ответ округлите до сотых.
Найдите корень уравнения (left(dfrac14right)^{x+2}=256^x)
Найдите значение выражения (log_{2{,}5}6cdotlog_60{,}4)
На рисунке изображен график функции y=f(x), определенной на интервале (-1;13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=-2.
Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1{,}4+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точке (A(x_0;y_0)). Найдите (y_0)
Найдите точку максимума функции (y=(2x-1)cos x-2sin x+9) принадлежащую промежутку (left(0;dfrac{pi}{2}right)).
а) Решите уравнение (log^2_2(4x^2)+3log_{0{,}5}(8x)=1)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}15;1{,}5])
Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что M – середина SB.
б) Найдите расстояние между прямыми AC и DM, если высота пирамиды равна 6√3.
Решите неравенство (dfrac{sqrt{x+4}left(8-3^{2+x^2}right)}{4^{x-1}-3}leqslant0)
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей. В ответ запишите количество миллионов.
Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной из вершины C. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что I и J лежат на отрезке EF.
б) Найдите расстояние от точки C до прямой IJ, если AC=15, BC=20.
Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}2=|x|) и (asqrt2+x=sqrt{2asqrt2x-x^2+12}) имеют ровно 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 68?
б) Может ли n равняться 86?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Решение и ответы заданий Варианта №7 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
Найдите корень уравнения log9 32x+9 = 2.
Задание 2.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 спортсмена из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России.
Задание 3.
Острый угол В прямоугольного треугольника равен 50°. Найдите угол между высотой СН и медианой СМ, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Задание 4.
Найдите значение выражения frac{a^{5,96}cdot a^{2,4} }{a^{5,36}} при а = 6.
Задание 5.
От треугольной призмы, объём которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объём оставшейся части.
Задание 6.
Прямая у = 5х + 11 является касательной к графику функции у = х3 + 4х2 + 9х + 11. Найдите абсциссу точки касания.
Задание 7.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 24 километров. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 32 километров?
Задание 8.
Первый садовый насос перекачивает 8 литров воды за 4 минуты, второй насос перекачивает тот же объём воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 60 литров воды?
Задание 9.
На рисунке изображён график функции f(x) = k√x + p. Найдите значение х, при котором f(х) = –10.
Задание 10.
Игральный кубик бросают дважды. Известно, что в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.
Задание 11.
Найдите точку максимума функции у = ln(х + 25)11 – 11х + 5.
Задание 12.
а) Решите уравнение 5sinx – 4sin3x = 2sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; -2pi ].
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = AC.
Ответ задания: б) 45°.
Задание 14.
Решите неравенство log22(x4) – 4log0,25 (x2) ≥ 12.
Задание 15.
Производство х тыс. единиц продукции обходится в q = 2х2 + 5х + 10 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении х?
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 13 и ВС = 10. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Ответ задания: frac{5}{3}.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Ответ задания: -frac{1}{2}; 2.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<3.
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{4}]+[frac{n}{7}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{4}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]+[frac{n}{17}]=n+1945?
Ответ задания: а) нет; б) да; в) 306.
Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Канал видеоролика: Математик МГУ
Смотреть видео:
#математикаогэ #гвэ #егэответы #репетиторпоматематике #репетитор_по_математике #огэматематика #огэответы #подготовкакогэ #подготовкакегэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Новый Профильный ЕГЭ 2023 математика Ященко вариант 1 (повышенная сложность)
Математик МГУ

Новый Профильный ЕГЭ 2023 математика Ященко вариант 3 (хардкор)
Математик МГУ

Новый Профильный ЕГЭ 2023 математика Ященко вариант 5 (супер сложность)
Математик МГУ

Решаем новый Профильный ЕГЭ 2022 математика Ященко вариант 1
Математик МГУ
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
30.10.2022
| 3636 | Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106°, угол CAD равен 69°. Найдите угол ABD. Ответ дайте в градусах |
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 1 | |
| 3635 | В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=6, AA1=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1 |
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=6, AA1=5 ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 2 | |
| 3634 | Найдите значение выражения cos α, если иtg(alpha)=-sqrt(21)/2 и alpha in ((3pi)/2; 2pi) |
Найдите значение выражения cos α, если tg α = — корень из 21 / 2 и α in (3 пи/2; 2пи) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 6 | |
| 3633 | На рисунке изображён график функции f(x)=k/(x+a). Найдите f(-7)
|
На рисунке изображён график функции f(x)=k / x+a Найдите f(-7) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 10 | |
| 3632 | Найдите точку максимума функции y= -(x^2+196)/x |
Найдите точку максимума функции y= — x2 + 196 / x ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 11 | |
| 3631 | В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6sqrt3 и BP=4 |
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 16 # Задача-аналог 2559 | |
| 3630 | Через концы A и B дуги окружности с центром O проведены касательные CA и CB. Угол CAB равен 39°. Найдите угол AOB. Ответ дайте в градусах |
Через концы A и B дуги окружности с центром O проведены касательные CA и CB ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 1 | |
| 3629 | Объём параллелепипеда ABCDA1B1C1D1 равен 60. Найдите объём треугольной пирамиды ACB1D1 |
Объём параллелепипеда ABCDA1B1C1D1 равен 60. Найдите объём треугольной пирамиды ACB1D1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 2 | |
| 3628 | Найдите корень уравнения log_{0.5}(x+5)=log_{2}(0.2) |
Найдите корень уравнения log0,5 (x+5) = log2 0,2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 5 | |
| 3627 | Найдите значение выражения (14^6.4*7^-5.4)/4^2.2 |
Найдите значение выражения 14^6.4*7^-5.4 /4^2.2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 6 | |

Показана страница 1 из 24
Наверх

Скачать бесплатно сборник Ященко И.В. ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с ответами и решением.
Скачать сборник Ященко ЕГЭ 2023 в PDF
Аннотация к сборнику «ЕГЭ 2023. Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
Ященко ЕГЭ 2023 математика профиль 36 вариантов
В сборнике представлены: -36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2023 года; — инструкция по выполнению экзаменационной работы; — ответы ко всем заданиям; — решения и критерии оценивания заданий 12-18.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ. Под редакцией И. В. Ященко.
-
Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
-
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30