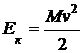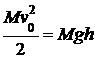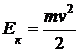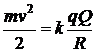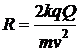Решение задач егэ части с кинематика - Помощь в подготовке к экзаменам и поступлению

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

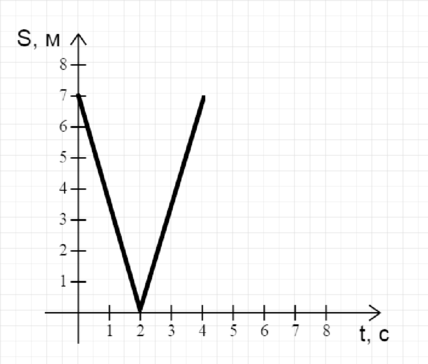
Из двух концов комнаты навстречу друг другу с постоянной скоростью движутся МО и Рыжий Боб. На графике показана зависимость расстояния между ними от времени. Скорость МО равна 3,14 м/с. С какой скоростью движется Рыжий Боб? (Ответ дайте в м/с)

По графику определяем, что расстояние между МО и Рыжим Бобом в начальный момент времени (S=7) м, а время, спустя которое они встретятся, (t=2) c. Перейдем в подвижную систему отсчета относительно МО. Тогда по закону сложения скоростей Рыжий Боб будет двигаться к нему со скоростью: [upsilon=upsilon_1+upsilon_2,] где (upsilon_1) и (upsilon_2) — скорости МО и Рыжего Боба соответственно (относительно неподвижной системы отсчета).
По закону равномерного прямолинейного движения: [S=upsilon t] Подставим сюда предыдущую формулу, и получим: [S=(upsilon_1+upsilon_2)t] Осталось выразить отсюда скорость Рыжего Боба: [upsilon_2=dfrac{S}{t}-upsilon_1=dfrac{7 text{ м}}{2~c}-3{,}14 text{ м/c} = 0{,}36 text{ м/c} .]

Ответ: 0,36

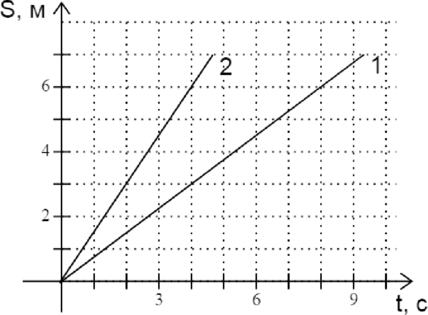
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела (upsilon_2) больше скорости первого тела (upsilon_1).

Т.к. пройденные пути тел линейно увеличиваются, тела движутся равномерно и прямолинейно.
По графику определяем, что первое тело за время (t_1=4) с проходит путь (S_1=3) м, а второе тело за время (t_2=2~c) проходит путь (S_2=3) м. По закону равномерного прямолинейного движения: [S_1=upsilon_1t_1
quad
S_2=upsilon_2t_2] Отсюда выразим (upsilon_1) и (upsilon_2): [upsilon_1=dfrac{S_1}{t_1}; quad
upsilon_2=dfrac{S_2}{t_2}.] Найдем (dfrac{upsilon_2}{upsilon_1}): [dfrac{upsilon_2}{upsilon_1}=dfrac{dfrac{S_2}{t_2}}{dfrac{S_1}{t_1}}=dfrac{dfrac{3 text{ м}}{2~c}}{dfrac{3 text{ м}}{4~c}}=2]

Ответ: 2

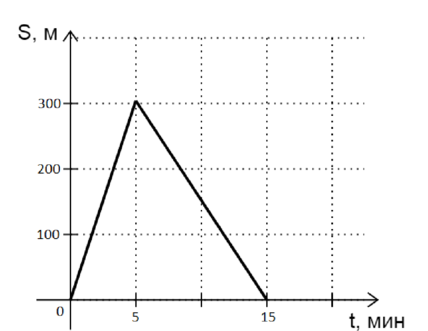
Дима каждый день ходит в школу. На рисунке представлен график движения Димы из дома в школу и обратно. Дом находится в точке (S=0), а школа — в точке (S=300) м. Чему равен модуль скорости Димы на пути из школы домой? (Ответ дайте в м/с)

Рассмотрим график: весь путь Дима двигался прямолинейно и равномерно (но в точке (S=300) м изменил свою скорость). Сначала он двигался из дома в школу со скоростью (upsilon_1) в течение времени (t_1=5) мин, после чего возвращался из школы домой cо скоростью (upsilon_2) в течение времени (t_2): [t_2=15text{ мин}-5text{ мин}=10text{ мин}=10cdot60text{ c}=600~text{ с}.] Чтобы найти (upsilon_2), нам необходимо рассмотреть участок движения Димы по пути из школы домой ((S_2)).
По закону равномерного прямолинейного движения: [S_2=upsilon_2t_2,] где (S_2=0text{ м}-300text{ м}=-300text{ м}).
Отсюда выражаем (upsilon_2): [upsilon_2=dfrac{S_2}{t_2}=dfrac{-300~text{м}}{600~text{c}}=-0,5~text{м/с}] Значит, (|upsilon_2|=|-0,5|text{ м/с}=0,5text{ м/с })

Ответ: 0,5

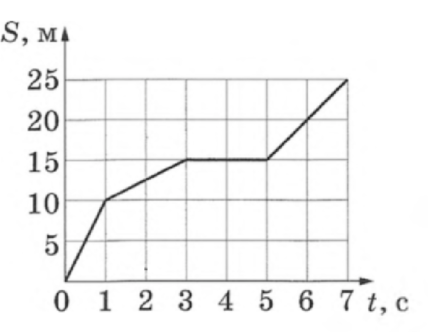
На рисунке представлен график зависимости пути (S), пройденного материальной точкой, от времени (t). Определите скорость (upsilon) точки на интервале времени от 5 с до 7 с. (Ответ дайте в м/с)

Т.к. пройденный путь материальной точки на интервале времени от 5 c до 7 c линейно увеличивается, материальная точка на этом интервале движется равномерно и прямолинейно. По закону равномерного прямолинейного движения:

[Delta S=upsilonDelta t,] где (Delta S=25 text{ м}-15text{ м}=10text{ м}), а (Delta t=7text{ c}-5text{ c}=2text{ c}). Выразим (upsilon): [upsilon=dfrac{Delta S}{Delta t}=dfrac{10text{ м}}{2text{ c}}=5text{ м/c}]

Ответ: 5

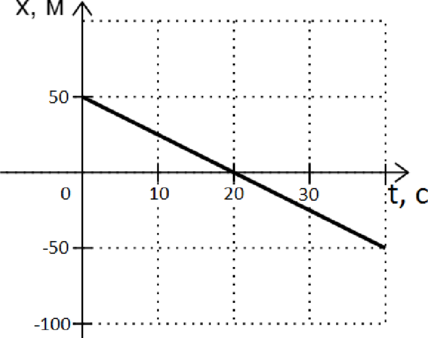
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении по оси Ox. Чему равна (upsilon_x) проекция скорости тела на ось Ох? (Ответ дайте в м/с)

Т.к. пройденный путь тела линейно уменьшается, тело движется равномерно и прямолинейно, и скорость тела постоянна: (upsilon_x=const). По закону прямолинейного равномерного движения тела: [Delta S=upsilon_xDelta t,] где (Delta S=-50text{ м}-50text{ м}=-100) — перемещение тела, а (Delta t=40 c) — время перемещения.
Отсюда выразим (upsilon_x): [upsilon_x=dfrac{Delta S}{Delta t}=dfrac{-100text{ м}}{40text{ c}}=-2,5~dfrac{text{м}}{text{c}}]

Ответ: -2,5

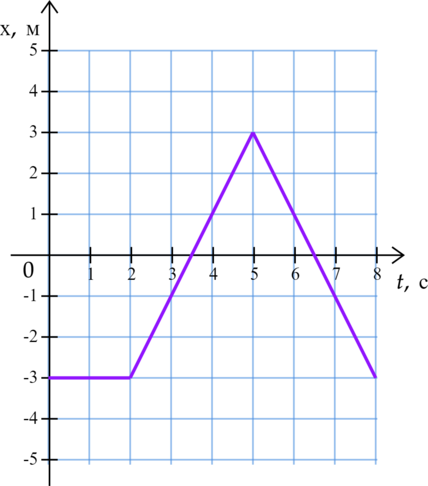
На рисунке приведен график зависимости координаты тела от времени при прямолинейном движении по оси (x). Какова проекция (upsilon_x) скорости тела в промежутке от 5 (c) до 8 (c)? (Ответ дайте в м/с)

Найдем изменение координаты тела в промежутке от 5 (c) до 8 (c). Для этого из конечной координаты вычтем начальную: [Delta x=x_text{к}-x_text{н}]

Подставим исходные данные: [Delta x=(-3)text{ м}-3text{ м}=-6text{ м}]

Найдем изменение времени в промежутке от 5 (c) до 8 (c): [Delta t=t_text{к}-t_text{н}]

Подставим исходные данные: [Delta t=8text{ с}-5text{ с}=3text{ c}]

Найдем проекцию скорости тела:

[upsilon_x=frac{Delta x}{Delta t}]

Подставим исходные данные: [upsilon_x=frac{-6text{ м}}{3text{ c}}=-2text{ м/c}]

Ответ: -2

Движение двух велосипедистов задано уравнениями (x_1=3t) (м) и (x_2=12-t) (м). Велосипедисты двигаются вдоль одной прямой. Найдите координату (x) места встречи велосипедистов. (Ответ дайте в метрах)

1 способ:
Велосипедисты встретятся, если совпадут их координаты, отсюда: [x_1=x_2]
Подставим уравнения: [3t=12-t] [4t=12]
Отсюда время, в которое встретятся велосипедисты: [t=3text{ c}]
Найдем координату (x) места встречи велосипедистов, для этого подставим время (t) в оба уравнения: [x_1=3cdot3=9text{ м}] [x_2=12-3=9text{ м}]
2 способ:
Изобразим движение велосипедистов: 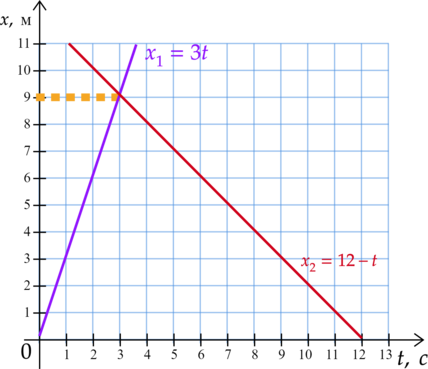Найдем пересечение графиков и опустим перпендикуляр к оси (oY). Отсюда очевидно, что ответ 9 м.

Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Тема 30.

Механика (Расчетная задача высокого уровня сложности+обоснование)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

механика (расчетная задача высокого уровня сложности+обоснование)

30.01Кинематика

30.02Динамика

30.03Законы сохранения в механике

30.04Статика

30.05Гидростатика

30.06Механические колебания

Решаем задачи

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

3. В условии данной задачи пренебрегаем силой сопротивления воздуха, также по условию задачи
соударения мгновенные и абсолютно упругие, можно сделать вывод о том, что при соударении энергия
не выделяется, поэтому в данной задаче можно использовать закон сохарнения энергии для
описания движения шарика. За нулевой уровень потенциальной энергии примем поверхность
земли.

4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна − g , поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.

Решение

Так как соударения абсолютно упругие, то траекторию можно перерисовать в виде параболы с
ветвями вниз.

Из Закона сохранения энергии скорость тела в начальный момент времени

mv2 mv20 ∘ ---------
-----= mgh + -----⇒ v = v20 + 2gh
2 2

Рассмотрим оси и . По оси начальная скорость v0y , при этом в высшей точки полета
она будет равна нулю, а время подъема будет равно половине время полета, следовательно, из
уравнений кинематики

0 = v0y − gt ⇒ v0y = gt
2 2

Начальная скорость тела будет равна

∘ ---------
2 2
v = v0x + v0y

Откуда начальная скорость по оси

∘ ------2-
v0x = v2 − v0y

А дальность полета () находится по формуле

Откуда

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что по горизонтали тело движется равномерно, а по вертикали — равноускоренно.
3. Указано, что тело является материальной точкой.
4. Обоснована возможность использования закона сохранения энергии.
5. Введен нулевой уровень потенциальной энергии

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.

III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).

IV) Получен верный ответ.

2 балла ставится если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

4. Так как сопротивление воздуха отсутствует, то полная механическая энергия тела не изменяется,
значит можно использовать закон сохранения энергии для описания движения тела. За нулевой уровень
потенциальной энергии примем поверхность земли.

5. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна − g , поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.

Решение

По горизонтали тело пролетит

L = v0t

По вертикали

gt2
h = --- (1)
2

Так как по условию L = 3h , то имеем

gt2 2v 2 ⋅ 3 м/с
v0t = 3---⇒ t = ---0= ---------2-= 0, 2 с
2 3g 3 ⋅ 10 м/с

Скорость тела найдем из закона сохранения энергии

mv20- mv2--
2 + mgh = 2 ,

где – искомая величина, – масса тела.
Откуда скорость тела перед падением с учетом (1)

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Обоснована возможность применения закона сохраненя энергии.
3. Движение тела вдоль горизонтальной оси будет равномерным, а вдоль вертикальной оси –
равноускоренным с ускорением g.
4. Обоснована возможность применения к телу модели материальной точки.
5. Введен нулевой уровень потенциальной энергии

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула для нахождения
пути тела при его равномерном движении вдоль горизонтальной оси и формула для пути
тела при его равноускоренном движении вдоль вертикальной оси, получены формулы для
движения тела с учетом начальных значений скоростей по осям и углу наклона вектора
начальной скорости к горизонту, записан закон сохранения энергии для нахождения скорости
тела в момент удара (или записано выражение для вертикальной составляющей вектора
скорости в момент удара, конечная скорость тела представлена в виде векторной суммы
горизонтальной и вертикальной составляющих, получено выражение для нахождения модуля вектора
конечной скорости тела в момент удара, записаны формулы кинетической и потенциальной
энергии).

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с и
направленным вертикально вниз. Ось направлена вертикально вверх. Так как сопротивлением
воздуха пренебрегаем, то описывать движение шарика будем с помощью закона сохранения
энергии, так как диссипативные силы отсутсвуют и действует только сила тяжести, которая
является потенциальной. За нулевой уровень потенциальной энергии примем поверхность
земли.

Решение

Запишем закон сохранения энергии

mv20 mv2
-----+ mgh = ----,
2 2

где – начальная скорость камня, – масса камня.
Найдем начальную скорость камня

По условию скорость камня в начальный момент времени и конечный направлены под углом 120∘ ,
отложим вектора этих скоростей из одной точки, при этом изменение скорости камня будет равно
величине . Будет треугольник, составленный на сторонах , , и , при этом будет лежать
напротив угла ∘
120 .

Откуда по теореме косинусов

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что по горизонтали тело движется равномерно, а по вертикали — равноускоренно.
3. Сказано, что тело является материальной точкой.
4. Обоснована возможность применения закона сохранения энергии.
5. Введен нулевой уровень потенциальной энергии

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Из точки, находящейся над землёй, одновременно бросили два тела: одно вертикально вверх с начальной
скоростью v0 = 10 м/с, второе — горизонтально с начальной скоростью 2v0 . Найти расстояние
между телами в тот момент, когда первое тело поднялось на максимальную высоту над
поверхностью земли. Второе тело в этот момент времени ещё не успело упасть на землю.

(«Росатом», 2012, 11)

Показать ответ и решение

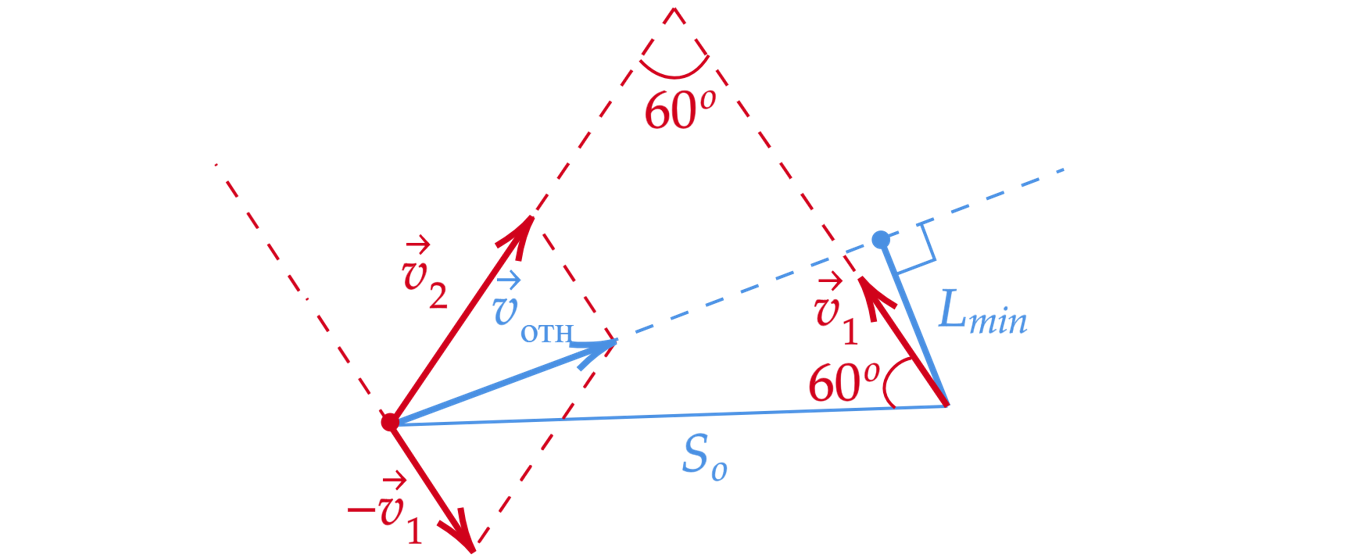
I способ
Перейдем в систему отсчета, связанную с первым кораблем.
Тогда относительная скорость равна

v⃗ = ⃗v − ⃗v
отн 2 1

Чтобы найти угол рассмотрим треугольник со сторонами Угол между сторонами и
v
2 равен 60 По теореме косинусов

∘ ----------------------
v отн = v2 + v2 − 2v1v2cos 60∘ = 26 м/с
1 2

По
теореме синусов найдем

v1 v отн v1 sin 60∘ 1
-----= ------∘ ⇒ sin γ = --------- = --
sin γ sin 60 v отн 2

А угол равен , значит, траектория относительного движения является
биссектрисой, а в равностороннем треугольнике она является еще и медианой, следовательно,
Lmin = S0-= 10
2

II способ
До момента пересечения траекторий корабли будут сближаться, после пересечения траекторий корабли
будут удаляться. Значит минимальное расстояние в точке пересечения траекторий. Так как скорость
второго в 2 раза больше, чем скорость первого, то он придет в точку пересечения в 2 раза быстрее, а
расстояние между кораблями будет равно половине траектории. Заметим, что треугольник
равносторонний (равнобедренный, с углом при пересечении одинаковых ребер 60 градусов), значит
длина траектории равна =20 км. Так как расстояние между кораблями равно S0-
2 =10
км.

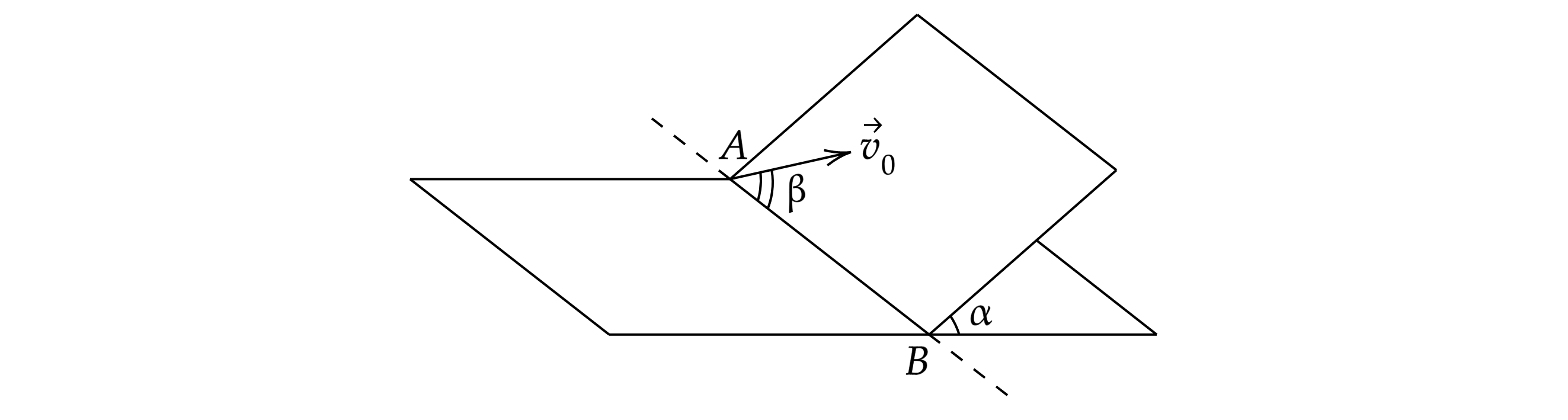
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой . Угол между плоскостями ∘
α =30 . Маленькая
шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью v0 = 2 м/с под углом к
прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной
плоскостью, найдите расстояние AB.

Сборник задач «1000 задач»

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в этой СО.

2. Движение тела поступательное, поэтому будем считать его материальной точкой.

3. В условии данной задачи пренебрегаем силой трения, поэтому тело движется только под действитем силы тяжести с
ускорением свободного падения, равным м/с и направленным вертикально вниз. Ось направлена перпендикулярно
прямой по наклонной плоскости. Ось направим по прямой .

4. Проекция ускорения на ось равна , поэтому описывать движение по этой оси будем с помощью законов
прямолинейного равноускоренного движения. Проекция ускорения на ось равна 0, поэтому описывать движение по горизонтали
будем с помощью законов прямолинейного равномерного движения.

Решение

Ось направим по прямой , ось – вверх по наклонной плоскости перпендикулярно линии . Найдем проекции
вектора ускорения свободного падения на оси

Движение по наклонной плоскости эквивалентно движению тела, брошенного под углом бета к горизонту, в поле тяжести с
ускорением .
Уравнения движения вдоль осей x и y:

В момент времени , соответствующий концу движения, и . Используя это условие для решения системы
уравнений, получаем

2v20sin βcosβ 2√3-
AB = ---gsin-α---= --5-

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что по выбранным координатным осям тело будет двигаться равноускоренно.
3. Обоснована возможность применения к телу модели материальной точки.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Скорость мальчика при разгоне описывается уравнением:

где v = v0 – конечная скорость, V = 0 – начальная скорость, – ускорение, – время движения.
Из этого уравнения можно выразить время разгона:

v
t1 = a0.

Расстояние, которое пробежит мальчик во время разгона равно:

2 2 2
S = Vt+ at1= at1-= v0.
2 2 2a

Тогда на границе разгона расстояние от мальчика до ворот равно l− S , а движение равномерное, значит, время движения
мальчика при равномерном движении равно:

t2 = l− S-.
v0

Полное время движения

Из этой формулу видно, что меньше ускорение мальчика, тем больше время движения. Время движения не должно превышать
время опускания решетки . Для того, чтобы мальчик успел пробежать, необходимо, чтобы ворота опустились на высоту, не
превышающую рост мальчика , то есть время опускания ворот равно:

τ = H-−-h.
u

Максимальность времени движения мальчика (минимальность ускорения) будет достигнута при t =τ , то есть

Подставим числа из условия

2,5 м/с
amin =-(-3 м-−-1 м--20-м-)-= 0,625 м/с2
2 -0,2-м/с-− 2,5 м/с

Стартуя из точки А (см. рисунок), спортсмен движется равноускоренно до точки В, после которой
модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время,
затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения на обоих
участках одинаков? Траектория ВС – полуокружность. Какие законы Вы использовали для описания
движения? Обоснуйте их применение к данному случаю.
Сборник задач «1000 задач»

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

3. На учаскте разгона тело движется прямолинейно с постоянным ускорением.

4. После окончания разгона тело будет с постоянной скоростью по окружности и будет обладать
центрострмеительным ускорением.

5. Движение тела на обоих участках будем описывать законами равноускоренного движения.

Решение

Рассмотрим прямолинейный участок. На нём ускорение определяется формулой:

v − v0
a1 = ------,
t1

Ускорение на прямолинейном участке определяется формулой

a1 = -v,
t1

где – скорость в точке , – скорость в точке , а – время движения по
прямолинейному участку.
Так как спортсмен стартует из точки , то v
0 и формулу можно преобразовать в

v
a1 = --
t1

Рассмотрим движении по дуге окружности. Так как скорость спортсмена при движении по
полуокружности постоянна, то тангенциальная составляющая ускорения равна нулю и ускорение
при движении по окружности можно считать центростремительным, а его можно найти по
формуле:

2
a2 = v--,
R

где – радиус полуокружности.
С учетом того, что период обращения равен

2πR
T = ----.
v

При это период обращения равен движению по полному кругу, а в условии полуокружность, то –
пол периода, следовательно, πR--
v = t2 , откуда

vπ
a2 = ---
t2

Так как по условию модули ускорений на участках равны, то приравнивая выражения для
ускорений, получим

v vπ t
-- = --- ⇒ -2= π
t1 t2 t1

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Сказано, что тело можно считать материальной точкой.
3. Сказано, что после прекращения разгона тело движется с постоянной скоростью по окружности и
обладает центростремительным ускорением.
4. Сказано, что описывать движение тела можно, используя законы равноускоренного движения.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

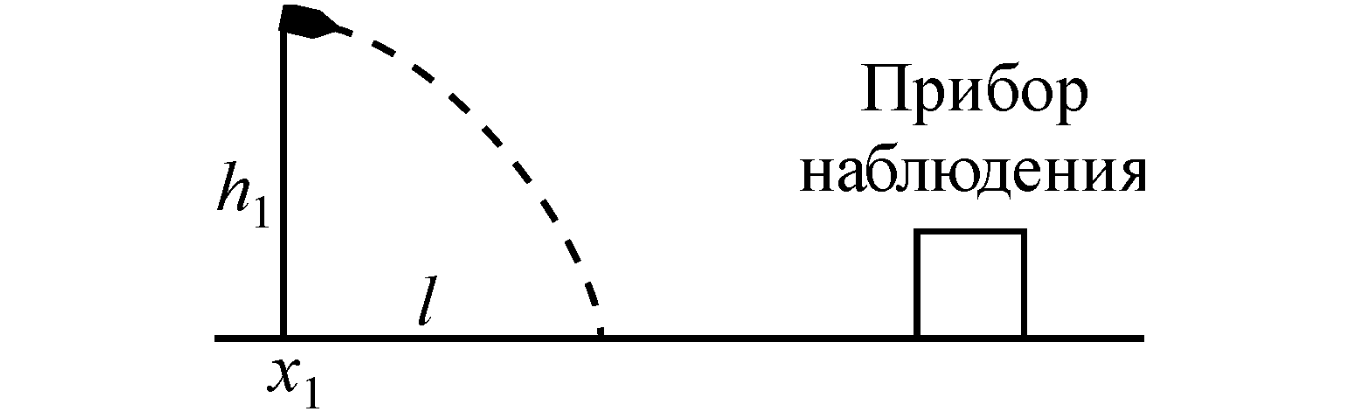
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и
высоту = 1655 м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на
расстоянии = 1700 м от места его обнаружения. Известно, что снаряды данного типа вылетают из
ствола пушки со скоростью 800 м/с. На каком расстоянии от точки взрыва снаряда находилась пушка,
если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на
одной горизонтали. Какие законы Вы использовали для описания движения? Обоснуйте их применение
к данному случаю.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

Решение

Найдем горизонтальную проекцию скорости l
vx = - = v0 cosα
t , где – последние 3 секунды полета,
– начальная скорость полета, – угол выстрела пушки.

∘ -------
v = v2x + v2y,

где – вертикальная проекция скорости.
А значит в начальный момент времени вертикальная проекция скорости равна

∘ -------
v0y = v20 − v2x = v0sin α

Воспользуемся уравнением скорости для вертикальной оси

v sin α
vy = v0 sin α − gt1 = 0 ⇒ t1 = -0-----
g,

где – время падения снаряда.
Так как время подъема камня равно времени падения камня, то общее время полета равно t = 2t1 , а
уравнения координаты на горизонтальную ось выглядит следующим образом

Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту,
достиг максимальной высоты 5 м и упал обратно на землю в 20 м от места броска. Чему равна
минимальная скорость камня за время полёта? Какие законы Вы использовали для описания движения?
Обоснуйте их применение к данному случаю.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

Решение

В случае броска под некоторым углом, скорость будет раскладываться на 2 компонента

∘ -------
2 2
v = vx + vy

где v
x – горизонтальная проекция скорости, v
y – вертикальная проекция скорости. Так как
горизонтальная проекция всегда постоянна, то для минимальности нужно, чтобы вертикальная
проекция была равна нулю, то есть в наивысшей точке полета. Воспользуемся уравнением скорости для
вертикальной оси

где – угол броска камня, – время подъема камня на максимальную высоту. Подставим в
уравнение координаты на вертикальную ось

gt21 2 gt21 gt21
h = v0sin αt − 2 = gt1 − 2 = 2

Выразим отсюда время подъема камня

∘ ---
t = 2h-
1 g

Так как время подъема камня равно время падения камня, то общее время полета равно t = 2t1 . По
горизонтальной оси скорость тела постоянна, а это означает, что путь, пройденный телом
равен

Выразим отсюда скорость по горизонтали

∘ --- ∘ -------2
vx = L--= -∘L---= L- -g- = 20-м- 10-м/-с- = 10 м/ с
2t1 2 2h- 2 2h 2 2 ⋅ 5 м
g

Критерии оценки

Критерий 1

1 балл ставится если

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

С некоторой высоты над поверхностью земли бросили груз без начальной скорости. Расстояние, которое
преодолел груз в последнюю секунду своего падения, оказалось на 10% больше пути, который он прошёл
в предыдущую секунду. Сколько времени падал груз? Ускорение свободного падения = 10 м/с
Сопротивлением воздуха пренебречь. Какие законы Вы использовали для описания движения?
Обоснуйте их применение к данному случаю.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

4. Проекция ускорения на ось равна , поэтому описывать движение по вертикали будем с
помощью законов прямолинейного равноускоренного движения.

Решение

Пусть всё время движения составляет секунд . Тогда за секунд тело пройдет

2
S = v t + gt-
0 2

за время

g(t −-1)2
S1 = v0(t − 1) + 2

а за время

g(t − 2)2
S2 = v0(t − 2) + ---------
2

так как начальная скорость тела равна 0, то

2
S = gt2-
g(t−1)2
S1 = 2 2
S2 = g(t−22)-

Так как по условию

имеем

2 2 ( 2 2)
gt- − g-(t-−-1)- = 1,1 g(t −-1)-− g-(t −-2)
2 2 2 2

( )
t2 − t2 + 2t − 1 = 1,1 t2 − 2t + 1 − t2 + 4t − 4

2,3
t = ----= 11,5 с
0,2

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что по вертикали тело движется равноускоренно.
3. Сказано, что тело является материальной точкой.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

Решение

1. Введем оси и , по оси мяч движется равномерно со скоростью , а по оси
равноускоренно вниз с ускорением , при этом скорость движения в момент времени
равна

∘ ----------
∘ -2----2 2 2
v = vx + vy = v0 + (gτ)

Откуда начальная скорость

2. Проанализируем, до какого момента мяч будет удаляться от склона, а будет удаляться до тех пор,
пока скорость не составит с горизонтом такой же угол, как и склон. Отложим вектора начальной и
конечных скоростей из одной точки, при этом изменение скорости камня будет равно величине .
Будет треугольник, составленный на сторонах v
0 , , и , при этом будет лежать напротив угла
(см. рис.)

Откуда тангенс угла

1
12 м/с ⋅√---
tgα = gt ⇒ t = v0tgα-= ----------3-≈ 0,7 с
v0 g 10 м/с2

3. Введем ось ′
Oy перпендикулярную поверхности склона, тогда для это оси перемещение мяча по
Oy ′ :

gcos αt2
H = v0sinαt − ---------
2

Подставим значение из пункта 2:

( )
v0tgα gcos α v0tg α 2 v20 sin2 α v20 sin2 α v20 sin2α
H = v0 sin α ⋅------− ------- ------ = -------- − -------- = --------
g 2 g gcos α 2g cosα 2gcos α

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что по вертикали тело движется равноускоренно, а по горизонтали — равномерно.
3. Сказано, что тело является материальной точкой.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

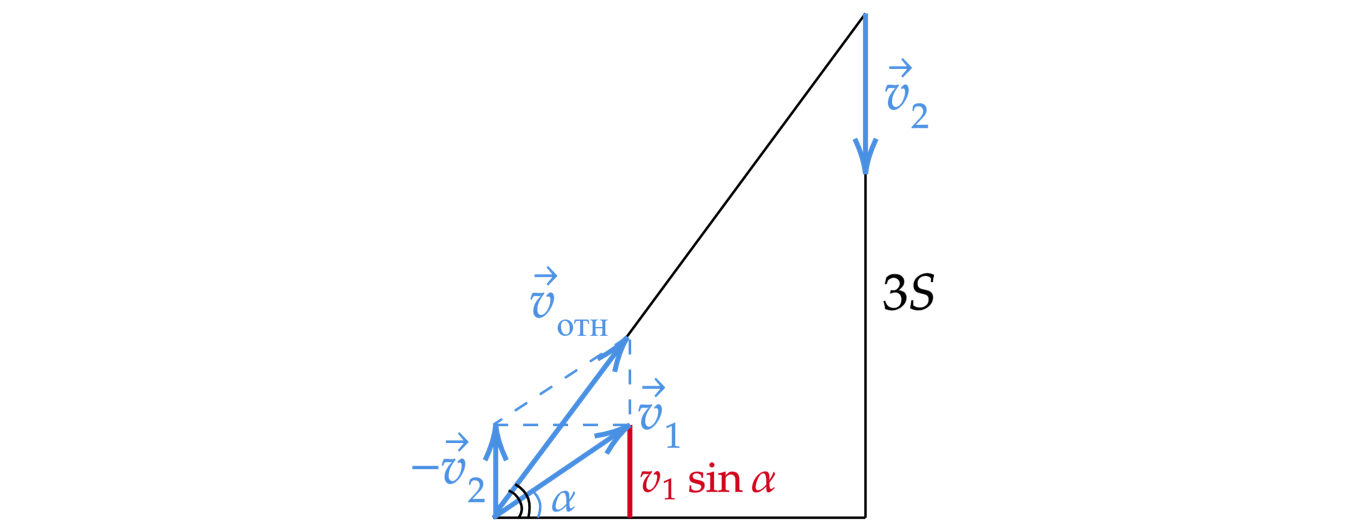
I способ
Перейдем в систему отсчета, связанную со вторым телом.
Если перейдем в систему отсчета, связанную со вторым, то первому телу надо будет пройти
3S по вертикали и S по горизонтали. Тогда скорость первого тела, относительно второго
равна

, а
ускорение равно нулю.
При этом угол наклона относительной скорости таков, что его тангенс равен 3 (потому что по
вертикали 3S, а по горизонтали S) Тангенс можно расписать как

v1 sin α + v2 4 3
tg β = 3 = ---v-cosα--- ⇒ v2 = v1(3cos α − sin α) = 5 м/ с (3 ⋅5-− 5) = 9 м/с
1

II
способ
Найдем sinα через основное тригонометрическое тождество

∘ -------
√ -------2-- 16- 3-
sinα = 1 − cos α = 1 − 25 = 5

Перейдем в систему отсчета, которая движется с ускорение вниз.
Рассмотрим движение снежинки и снежинки относительно горизонтальной оси этой системы
и вертикальной .
Снежинка :
По горизонтально оси она пролетит расстояние с постоянной скоростью

Это
расстояние равно

По
вертикальной оси она также будет двигаться без ускорения (с учетом нашей системы отсчета).И ее
скорость при этом равна

Пусть она будет на расстоянии по вертикали от начала своего движения, с учетом формул
кинематики имеем

Теперь рассмотрим снежинку .
По горизонтальной оси она не будет двигаться, а по вертикальной будет двигаться с постоянной
скоростью и пройдет расстояние . С учетом формул кинематики

Выразим из (1) время движения снежинок и объединим (2) и (3)

---S----
t = v1 cosα

v1sinα v2S
3S − --------= --------
v1cos α v1 cosα

Поделим на и выразим

4- 3-
v2 = v1(3cosα − sin α) = 5 м/ с (3 ⋅5 − 5) = 9 м/с

В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета
дует постоянный боковой ветер перпендикулярно линии полета, то самолет затрачивает на перелет на 9
минут больше. Найдите скорость ветра, если скорость самолета относительно воздуха постоянна и равна
328 км/ч. Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному
случаю.
Сборник А. И. Черноуцан

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

3. В условии данной задачи считаем движение тела равномерным, будем использовать законы
прямолинейного равномерного движения для описания движения тела.

Решение

В первой случае самолет пролетел расстояние

где – скорость самолета, – 6 часов.
Во втором случае скорость самолета относительно земли будет складываться из скорости самолета и
скорости ветра, при этом сложение будет векторное. То есть

∘ -------
v = v21 − v22

– скорость ветра. А расстояние, пройденное самолетом равно

∘ -------
S = vt = v2 − v2t
2 1 2 2

Отсюда

∘ ------- ∘ 2----2-
v1t1 = v21 − v22t2 ⇒ v2 = v1---t1-−-t2 = 72 км/ ч
t2

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Указано, что движение тела равномерное.
3. Сказано, что тело является материальной точкой.

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Велосипедисты едут колонной со скоростью 5 м/с. Длина колонны равна 210 м. Навстречу им бежит
тренер со скоростью 2 м/с. Поравнявшись с тренером велосипедист резко разворачивается и едет в
обратном направлении с той же скоростью. Чему будет равна длина колонны после того, как все
велосипедисты развернутся?

Показать ответ и решение

Перейдем в систему отсчета, связанную с движением тренера.
Тогда скорость сближения колонны с тренером равна

где
– скорость колонны, – скорость тренера.
Полный разворот колонна сделает за время

L
t = -- (2)
v0

–
первоначальная длина колонны.
После разворота каждый участник колонны будет удаляться от тренера с постоянной скоростью

v′ = v1 − v2, (3)
0

При
этом длина колонны после разворота будет равна

′ ′
L = v0t (4 )

Тогда с учетом (1), (2), (3) формулу (4) можно переписать в виде

v1 − v2 5 м/с − 2 м/ с
L′ = L------- = 210 м -------------- = 90 м
v1 + v2 5 м/с + 2 м/ с

Показать ответ и решение

Сначала найдем время полета шарика до удара о потолок:

gt21
h = v0t1 − 2

При
подстановке значений получаем квадратное уравнение, из которого c.

Теперь найдем скорость, которую шарик имел после 0,3 секунды полета:

2
v = v0 − gt1 = 5 м/с − 10 м/ с ⋅ 0, 3 c = 2 м/ с

После удара о потолок шарик абсолютно упруго отталкивается, то есть начинает лететь вниз с
начальной скоростью 2 м/с. Запишем уравнение его движения до приземления:

gt2
0 = H − v1t − 2

При
подстановке значений получаем квадратное уравнение:

2
5t + 2t − 2,25 = 0

Решив его, мы получим, что .

Осталось посчитать полное время полета шарика:

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.

2. Движение тела поступательное, поэтому будем считать тело материальной точкой.

3. На учаскте разгона тело движется вертикально вверх с постоянным ускорением.

4. После окончания разгона тело будет двигаться в поле силы тяжести и именно эта сила сообщает
телу ускорение направленное вертикально вниз и равное м/с.

5. Движение тела на обоих участках будем описывать законами прямолинейного равноускоренного
движения.

Решение

Сначала ракета двигалась равноускоренно вверх. Запишем формулу движения до момента
прекращения ускорения и формулу движения:

at2
h1 = ---
2

А скорость в конце разгона составит

v = at

После этого она находилась в свободном полете под действием силы тяжести, в ходе чего
остановилась в воздухе на высоте:

gt2
h2 = h1 + vt2 − --2,
2

где — начальная скорость на этом участке.

Выразим (время от момента прекращения ускорения до момента остановки ракеты) по формуле
конечной скорости:

v
t2 = --
g

Отсюда:

v-2
v g ⋅ (g)
h2 = h1 + v ⋅--− --------
g 2

Подставим формулу для :

v
2 2 g ⋅ (-)2
h = at- + v--− ----g---
2 2 g 2

После этого ракета начнет падать вниз, пока не упадет:

gt20
0 = h2 − ---
2

2
h = gt0
2 2

2 v2- 2
at + g = gt0

Осталось выразить :

Критерии оценки

Критерий 1

1 балл ставится если

1. Введена инерциальная система отсчета
2. Сказано, что тело можно считать материальной точкой.
3. Сказано, что после прекращения разгона тело движется в поле силы тяжести с ускореним свободного
падения.
4. Сказано, что описывать движение тела можно, используя законы прямолинейного равноускоренного
движения

__________________________________________________________________________________________________________________________________

В остальных случаях ставится 0 баллов по данному критерию.

При отсутствии обоснования по данному критерию ставится 0 баллов

Критерий 2

3 балла ставится если:

IV) Получен верный ответ.

2 балла ставится если:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится если:

Во всех остальных случаях за задачу выставляется 0 баллов.

В момент, когда опоздавший пассажир вышел на перрон вокзала, с ним поравнялось начало
предпоследнего вагона уходящего поезда. Желая определить, насколько он опоздал, пассажир измерил
время t
1 , за которое мимо него прошел предпоследний вагон, и время t
2 , за которое мимо него
прошел последний вагон. Оказалось, что t1 = 9 с, а t2 = 8 с. Считая, что поезд двигался
равноускоренно и длина вагонов одинакова, найти, на какое время пассажир опоздал к отходу
поезда.

Показать ответ и решение

Пусть — длина одного вагона, — ускорение поезда.
В момент прихода пассажира поезд проехал путь, равный:

2
S1 = aτ--
2

Когда проехал предпоследний вагон, путь стал равен:

a ⋅ (t + τ )2
S1 + S = -----1------
2

Выразим отсюда длину вагона:

Когда проехал последний вагон, путь стал равен:

a ⋅ (τ + t1 + t2)2
S1 + 2S = ----------------
2

Отсюда также выразим :

Длины вагонов равны, значит:

Осталось выразить отсюда :

2 2 2 2
τ = t2 +-2t1t2 −-t1-= (8-c)--+-2-⋅ 9-c ⋅ 8-c-−-(9-c)-= 63,5 c
2(t1 − t2) 2 ⋅ (9 c − 8 c)

Показать ответ и решение

Запишем уравнение торможения, сразу отметив, что ускорение отрицательно, т.к. направлено против
движения автомобиля:

2 2
S = v-−--v0
− 2a

Конечная скорость v = 0 . Отсюда:

2
S = v0-
2a

Выразим ускорение:

v2 400 м2/с2
a = -0-= ----------= 2 м/ с2
2S 200 м

Запишем формулу для скорости при равнозамедленном движении:

Отсюда:

Теперь запишем уравнение тормозного пути, при котором автомобиль прошел путь S/4 с тем же
ускорением:

S v2 − v2
--= -1----0
4 − 2a

Выразим :

Источник

: ЕГЭ по физике

Подборка заданий по кинематике для подготовки к ЕГЭ по физике в 11 классе.

→ Скачать задания

→ Скачать ответы

Данный тренинг соответствует разделу кодификатора 1. 1 — кинематика.

Этот раздел содержит 8 различных типов задач на разные темы. (1. 1. 1 — 1. 1.

В тренинге задачи подобраны в соответствие с кодификатором.

Пример заданий:

Камень падает с высокого обрыва, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени

1) увеличивается

2) уменьшается

3) не изменяется

4) сначала увеличивается, а затем начинает уменьшаться

Ответ: _____.

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Модуль скорости движения мотоцикла относительно автомобиля равен

1) 20 км/ч

2) 20 км/ч

3) 120 км/ч

4) 50 км/ч

Ответ: _____.

Связанные страницы:

Источник

Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.

В. З. Шапиро

Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.

Определение кинематических величин по графику

1. На рисунке приведён график зависимости проекции скорости тела от времени t.

Определите проекцию ускорения тела a_x в промежутке времени от 15 до 20 с.

Ответ: _________________________ м/с².Решение:

На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:

$a_x=frac{v_x-v_{0x}}{t}.$ Проведем расчет: $a_x=frac{-10-10}{5}=-4$ (м/с²).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.

Ответ: -4 м/с².

Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное $(a_{x } , textless ,0).$ Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.

Необходимая теория: Равноускоренное движение

2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.

Определите проекцию скорости тела в промежутке времени от 25 до 30 с.

Ответ: ___________________________ м/с.

Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:

$v_x=frac{x-x_0}{t}.$ Проведем расчет: $v_x=frac{0-10}{5}=-2$ (м/с)

Ответ: -2 м/с.

Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.

Необходимая теория: Вычисление перемещения по графику проекции скорости

3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.

Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.

Ответ: _________________________ м.

Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).

Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).

$S_1= frac{10+20}{2} cdot 10=150$ (м); $S_2= frac{10+20}{2} cdot 20=300$ (м);

(м).

Ответ: 450 м.

Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.

4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.

Определите проекцию перемещения тела за 10 с от начала наблюдения.

Ответ: ________________________ м.

Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.

$S_{1x}= frac{6+2}{2}cdot 10=40$ (м); $S_{2x}= frac{4cdot (-10)}{2}=-20$ (м); (м).

Ответ: 20 м.

При расчете $S_{2x}$ можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.

Относительность движения

5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?

Ответ: ________________________ м/с.

Формула для нахождения относительной скорости в векторной форме имеет вид:

Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:

С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.

, скорость первого автомобиля

Ответ: 15 м/с.

В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.

6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?

Ответ: ___________________________ м.

Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.

$S_{1x}=frac{8cdot 6}{2}=24$ (м); $S_{2x}=frac{8cdot (-4)}{2}=-16$ (м).

Знак «минус» для $S_{2x}$ показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.

$S_{1x}+S_{2x}=24+16=40$ (м).

Ответ: 40 м.

Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.

7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?

Ответ: ___________________________ км/ч

Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.

Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:

Ответ: 7,5 км/ч.

Равномерное движение тел по окружности

Необходимая теория: Равномерное движение по окружности

8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.

Ответ: ___________________________ м/с².

Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением Подставляя это выражение в первое уравнение и проводя сокращения, получим При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.

Проведем расчет:

Ответ: 118 м/с².

В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.

9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?

Ответ: ___________________________ Гц.

Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.

$v_1=frac{2pi R_1}{T_1}; v_2=frac{2pi R_2}{T_2}.$

Приравняем скорости и проведем сокращения.

$frac{2pi R_1}{T_1}=frac{2pi R_2}{T_2} ; frac{R_1}{T_1}=frac{R_1}{T_1};$ с учетом того, что период и частота величины обратные, запишем следующее равенство:

$R_{1 }vartheta_1=R_2vartheta_2$

$vartheta_2=frac{R_{1 }vartheta_1}{R_2}.$

Проведем расчет: $vartheta_2=frac{0,2}{0,1}cdot 2=4$ (Гц).

Ответ: 4 Гц.

В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.

10. Волчок, вращаясь с частотой 20 с^-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?

Ответ: ___________________________ оборотов.

Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой $h=frac{gt^2}{2};$ отсюда $t=sqrt{frac{2h}{g}}.$ Проведем расчет времени падения: $t=sqrt{frac{2cdot 5}{10}} =1$ (с). Так как волчок вращается с частотой 20 $c^{-1},$ то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.

Ответ: 20.

Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.

Если вы хотите разобрать большее количество заданий — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 1 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Примеры решений заданий части C ЕГЭ по физике.

ЕГЭ по физике с решениями, часть А

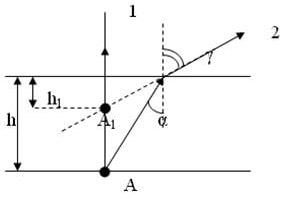
С1. Дно водоёма всегда кажется расположенным ближе к поверхностиводы для наблюдателя, находящегося в лодке. Объяснить это явление.

Ответ:

Образец возможного решения

Рассмотрим ход лучей 1 и 2, отражённых от некоторой точки А, лежащей на дне водоёма. Луч 1 (взятый для удобства построения) падает перпендикулярно на границу раздела сред (вода-воздух) и не преломляется. Произвольный луч 2 падает на границу раздела под некоторым углом α и преломляется под углом γ (α<γ, т.к. луч переходит из оптически более плотной среды в оптически менее плотную среду). Находим пересечение луча 1 и продолжения луча 2 – точку А₁. Из построения следует, что кажущаяся глубина h₁ меньше глубины водоёма h.

С2. Шар массой 1 кг свободно, без начальной скорости, падает с высоты 13,2 м. На высоте 10 м он насквозь простреливается горизонтально летящей пулей массой 10 г. Скорость пули за время движения в шаре изменяется от V₁=700 м/с до V₂=100 м/с. Найдите кинетическуюэнергию шара в момент удара о горизонтальную поверхность земли.

Ответ:

Образец возможного решения

Кинетическая энергия шара в момент его падения на землю определяется следующим образом: , где скорость шара v направлена под углом к горизонту, поскольку кроме вертикальной составляющей имеется еще и горизонтальная составляющая из-за взаимодействия с пулей.

;

Вертикальную составляющую скорости определяем из закона сохранения полной механической энергии: (h=13,2 м);

(поскольку пуля летела горизонтально, то взаимодействие с ней шара не скажется на вертикальной компоненте скорости);

Горизонтальную составляющую скорости шара определяем из закона сохранения импульса:

Е_к=150 Дж

С3. Как изменится температура идеального газа, если увеличить его объем в 2 разапри осуществлении процесса, описываемого формулой pV⁴=const?

Ответ:

Образец возможного решения

Выразим из уравнения Менделеева-Клапейрона давление p:

(1).

Подставим (1) в формулу, описывающую данный процесс:

https://5-ege.ru/reshenie-zadach-po-fizike-ege-chast-c/

; Следовательно, при увеличении объема в 2 раза температура должна понизиться в 8 раз

С4. Электрическое поле образовано двумя неподвижными, вертикальнорасположенными, параллельными, разноименно заряженными непроводящимипластинами. Пластины распложены на расстоянии d = 5см друг от друга. Напряженность поля между пластинами Е =10⁴В/м. Между пластинами, на равном расстоянии от них, помещен шарикс зарядом q = 10^-5 Кл и массой m = 20г. После того как шарикотпустили, он начинает падать и ударяется об одну из пластин. На какоерасстояние Δh по вертикалисместится шарик к моменту его удара об одну из пластин?

Ответ:

Образец возможного решения

Движение шарика можно «разложить» на равноускоренное движение по вертикали под действием силы тяжести и на равноускоренное движение по горизонтали под действием силы Кулона. За одно и то же время t шарик проходит путь (по вертикали) и (по горизонтали). Ускорение a находим по второму закону Ньютона: .

Таким образом,

С5. Маленький шарик массой 1 г, несущий заряд 0,15 мкКл, брошен издалека соскоростью 1 м/с в сферу, имеющую заряд 0,3 мкКл. При каком минимальном значениирадиуса сферы шарик достигнет ее поверхности?

Ответ:

Образец возможного решения

В момент бросания шарик обладает кинетической энергией , а его потенциальная энергия в электростатическом поле заряженной сферы равна нулю.

В тот момент, когда шарик достигнет поверхности сферы, его потенциальная энергия равна

, а кинетическая энергия равна нулю (из условия минимального значения радиуса сферы).

Применяя закон сохранения энергии, получаем

. Отсюда =0,81 (м)

С6. В вакууме находятся два покрытых кальцием электрода, к которым подключенконденсатор ёмкостью С. При длительном освещении катода светом с длиной волны λ=100нм фототок, возникший вначале, прекращается, а на конденсаторе появляется зарядq=9,6∙10^-10 Кл.Работа выхода электрона из кальция А=4,42∙10^-19 Дж. Определитеёмкость конденсатора С.

Ответ:

Образец возможного решения

Напряжение на конденсаторе U будет равно задерживающей разности потенциалов U_з, которое можно найти из уравнения Эйнштейна для фотоэффекта:

Отсюда: 9,6 В.

Находим емкость конденсатора: 100 пФ.

Рекомендуем:

Источник

Задачи по кинематике из ЕГЭ по физике с решениями

08.11.2014

Замечательный сборник различных задач по кинематике. Задачи ориентированы на подготовку к ЕГЭ по физике.

Все задачи имеют правильные ответы и решения. Уникальность материала в том, что задания сначала даются с подсказками. Т.е. вы сами можете всё решить, имея под рукой лишь подсказку. А затем просто сверить правильность ответа.

В конце файла представлены все необходимые формулы.

Автор-составитель: Левиев Г.И.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Источник