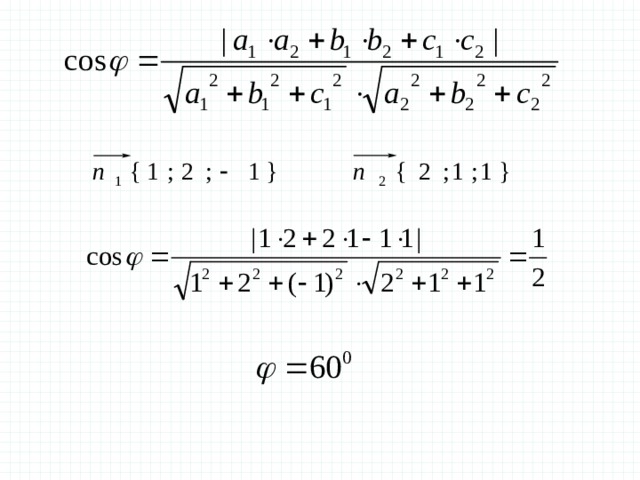Решение задач координатным методом 14 задание егэ

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

МБОУ «Раздорская СОШ им. А.П.Гужвина

Решение задач №14 ЕГЭ по математике координатно-векторным методом

Методические рекомендации

Серия «Школьник —
школьнику»

С.С.Уразалиева

Решение заданий
№14 ЕГЭ по математике координатно-векторным методом

Методические
рекомендации.

   С помощью
данных методических рекомендаций можно научиться решать задачи на вычисление
углов и расстояний в стереометрии с помощью координатно-векторного метода. Для
учеников 10-11 классов самой главной проблемой является подготовка к ЕГЭ.
Причем не все ученики уверенно решают задания II части , а
некоторые и не берутся за их решение.         

   Координатно-векторный 
метод  основан  на введении   прямоугольной системы координат и создании
геометрически-алгебраической модели решения задач, тем самым упрощая 
громоздкие и достаточно сложные преобразования и выкладки.

   Достоинство
метода координат состоит в том, что его применение избавляет от необходимости
прибегать к наглядному представлению сложных пространственных конфигураций.

   Выражаю
огромную благодарность своим ученикам 11 класса 2016 – 2017 учебного года:  Комаровой
Ангелине, Тарбаеву Наилю, Бекмурзаеву Тимуру, Утегеновой Аимгуль, Абылхатаевой
Карине, Кункашевой Арине, Юсуповой Аделине, Успанову Гелиму, которые
сыграли большую роль в создании данного методического сборника

Уважаемые ребята!

   Если у вас
имеются серьезные проблемы с пониманием определений, с  чтением или построением
сложного стереометрического рисунка, если вам  никак не удается подобрать
необходимые дополнительные построения, мне кажется, что стоит заняться
изучением координатно-векторного метода. Особенно это актуально в условиях
экстренной помощи, когда до ЕГЭ остается всего лишь 2-3 месяца.

   Данный курс не
претендует на научность, а является небольшим   методическим пособием при
подготовке к ЕГЭ для выпускника, нацеленного на высокий балл при сдаче
экзамена. Курс является кратким, в нем рассмотрены лишь наиболее часто
встречающиеся типы заданий, как в сборниках, так и в контрольно-измерительных
материалах.

   Метод координат
— это довольно несложный способ, но в настоящих задачах №14 никаких координат и
векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный
отрезок и направление осей x, y и z.

   Самое
замечательное свойство этого метода заключается в том, что не имеет никакого
значения, как именно вводить систему координат. Если все вычисления будут
правильными, то и ответ будет правильным.

   Успехов!

§1.
Основные понятия.

   Метод координат
—эффективный и универсальный способ нахождения любых углов или расстояний между
стереометрическими объектами в пространстве.  Данный метод заключается во
введении  декартовой системы координат, а затем – нахождение образующихся
векторов (их длин и углов между ними). Достоинство метода координат состоит в
том, что его применение избавляет от необходимости прибегать к наглядному
представлению сложных пространственных конфигураций. Алгоритм применения метода
координат к решению геометрических задач сводится к следующему:

—  Выбираем в
пространстве систему координат

—  Находим
координаты необходимых, по условию задачи, точек.

 —  Решаем задачу,
используя основные задачи метода координат.

 — Переходим от
аналитических соотношений к геометрическим.

    Для начала
разбора метода координат для стереометрических задач рассмотрим, что же
представляет собой прямоугольная (декартова) система координат в пространстве.
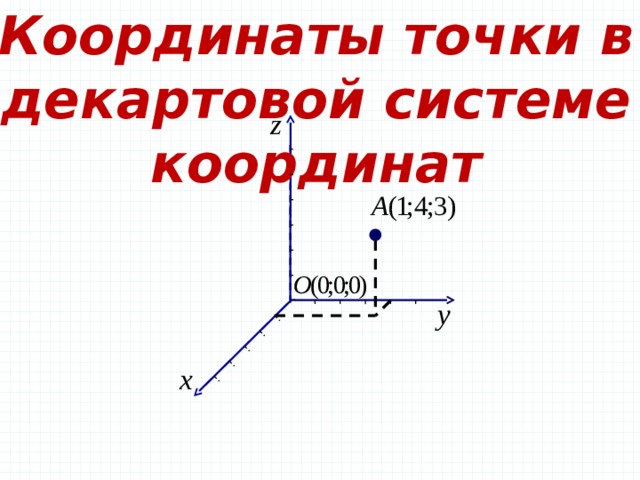
Прямоугольная (декартова) система координат в пространстве – совокупность точки
О (называемой началом координат), единицы измерения и трёх попарно
перпендикулярных прямых Ox, Oy иOz (называемых осями координат: Ox – ось
абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано
направление положительного отсчёта. Плоскости хОу, уОz и zOx называют
координатными плоскостями. Каждой точке пространства ставится в соответствие
тройка чисел, называемых её координатами.

  
                             z

                                  
0                                     у   

                     
х

Для того чтобы
использовать метод координат, надо хорошо знать формулы:

1. Нахождение
расстояния между двумя точками, заданными своими координатами.

 , где

D=AB,
A(x₁;y₁;z₁), B(x₂;y₂;z₂)

2. Нахождение
координат середины отрезка

A(x₁;y₁;z₁),
B(x₂;y₂;z₂)  
      

3. Нахождение
косинуса угла между векторами

 , где

4. Координаты x, y, z точки М, которая делит отрезок ,
ограниченный точками А(х₁, у₁,z₁ ) и B(x₂,y₂,z₂ ), в отношении , определяется по формулам

5. Расстояние от точки до плоскости

   Для решения задач необходимо научиться находить координаты вершин
основных многогранников при помещении их в прямоугольную систему координат.

   Ниже представлены координаты вершин некоторых многогранников,
помещенных в систему координат.

Координаты
куба

Это
самый простой многогранник, все двугранные углы которого равны 90°.

Система
координат также вводится очень просто:

1.        
Начало координат —
в точке A;

2.        
Чаще всего ребро куба не указано,
поэтому принимаем его за единичный отрезок;

3.        
Ось x направляем
по ребру AB, y — по ребру AD, а ось z —
по ребру AA₁.

Обратите
внимание: ось z направляется вверх! После двумерной системы координат это
несколько непривычно, но на самом деле очень удобно и логично.

Итак, теперь у каждой вершины куба
есть координаты. Соберем их в таблицу — отдельно для нижней
плоскости куба:

Точка	A	B	C	D
Координаты	(0; 0; 0)	(1; 0; 0)	(1; 1; 0)	(0; 1; 0)

И для верхней:

Точка	A1	B1	C1	D1
Координаты	(0; 0; 1)	(1; 0; 1)	(1; 1; 1)	(0; 1; 1)

Несложно заметить, что точки верхней плоскости отличаются от
соответствующих точек нижней только координатой z. Например,
B = (1; 0; 0), B₁ = (1; 0; 1).

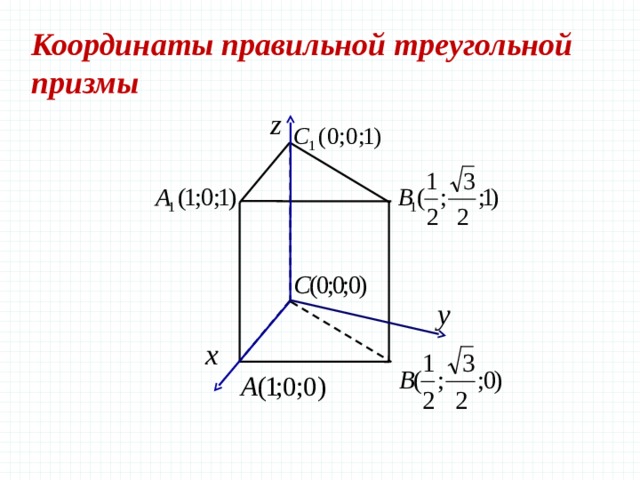
Координаты 
правильной треугольной призмы

При правильном подходе достаточно
знать координаты только нижнего основания — верхнее будет считаться
автоматически.

В задачах №14
встречаются исключительно правильные трехгранные призмы (прямые призмы,
в основании которых лежит правильный треугольник). Для них система
координат вводится почти так же, как и для куба.

Вводим
систему координат:

1.        
Начало координат —
в точке A;

2.        
Сторону призмы принимаем за единичный
отрезок, если иное не указано в условии задачи;

3.        
Ось x направляем
по ребру AB, z — по ребру AA₁, а ось y
расположим так, чтобы плоскость OXY совпадала с плоскостью
основания ABC.

Получаем
следующие координаты точек:

Как
видим, точки верхнего основания призмы снова отличаются от соответствующих
точек нижнего лишь координатой z. Основная проблема — это
точки C и C₁. У них есть иррациональные координаты, и
для того чтобы довольно просто решить задание №14 эти иррациональные координаты
надо просто запомнить. Или можно вывести.

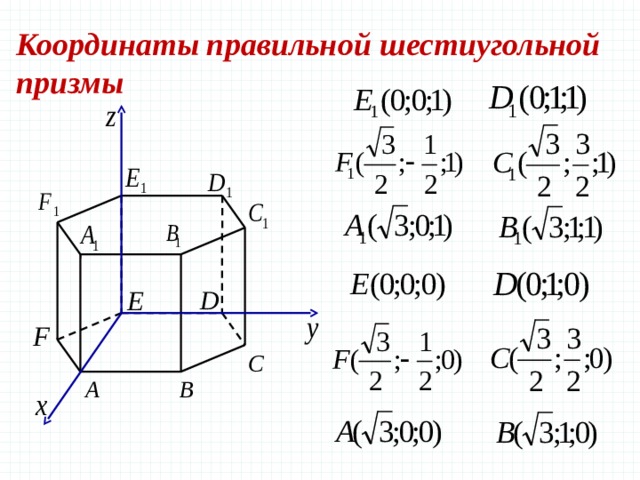
Координаты
 правильной шестиугольной призмы

Шестиугольная
призма — это «клонированная» трехгранная. Можно понять, как это
происходит, если взглянуть на нижнее основание — обозначим его
ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF.
Получилось шесть треугольников, каждый из которых (например,
треугольник ABO) является основанием для трехгранной призмы.

Теперь
введем систему координат. Начало координат — точку O — поместим
в центр симметрии шестиугольника ABCDEF. Ось x пойдет
вдоль FC, а ось y — через середины отрезков AB
и DE. Получим такую картинку:

Нужно
обратить внимание на то, что  начало координат не совпадает с вершиной
многогранника. На самом деле, при решении настоящих задач выясняется, что
это очень удобно, поскольку позволяет значительно уменьшить объем вычислений. Осталось
добавить ось z. Проводим ее перпендикулярно плоскости OXY
и направляем вертикально вверх. Получим картинку:

Запишем
теперь координаты точек. Предположим, что все ребра нашей правильной
шестигранной призмы равны 1. Итак, координаты нижнего основания:

Координаты
верхнего основания сдвинуты на единицу по оси z:

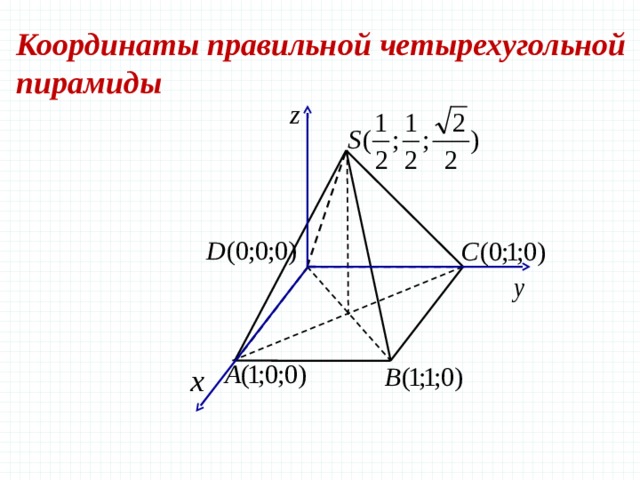
Координаты
 правильной четырехугольной пирамиды

Итак,
правильная четырехугольная пирамида. Обозначим ее SABCD,
где S — вершина. Введем систему координат: начало
в точке A, единичный отрезок AB = 1, ось x направим
вдоль AB, ось y — вдоль AD, а ось z — вверх,
перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется
высота SH — вот и построим ее. Получим следующую картинку:

Теперь
найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все
просто: в основании лежит квадрат, его координаты известны. Проблемы
возникают с точкой S. Поскольку SH — высота
к плоскости OXY, точки S и H отличаются лишь
координатой z. Длина отрезка SH — это и есть
координата z для точки S, поскольку
H = (0,5; 0,5; 0).

Заметим,
что треугольники ABC и ASC равны по трем сторонам
(AS = CS = AB = CB = 1,
а сторона AC — общая). Следовательно, SH = BH.
Но BH — половина диагонали квадрата ABCD, т.е.
BH = AB · sin 45°. Получаем координаты всех точек:

Ниже
представлено, как найти определитель третьего порядка по правилу Саррюса,
составить уравнение плоскости и найти вектор нормали.

§2
Практическая часть

Ниже представлены
задачи:

— на нахождение
угла между прямыми;

— угла между
прямой и плоскостью; 

— угла между плоскостями;

— расстояния от
точки до прямой;

— расстояния от
точки до плоскости.

Эти
задачи решили мои ученики 11 класса

Вариант 13. Задача
№14 по сборнику Ф.Ф.Лысенко

В кубе ABCDA₁B₁C₁D₁,
ребро которого равно 4, точка М является серединой отрезка BC₁.
Найдите расстояние между прямыми А₁В и АМ.

Задача №14 по
сборнику ФИПИ 2016

В правильной
шестиугольной призме ABCDEFA₁B₁C₁D₁
E₁F₁
все рёбра равны 1. Найдите расстояние от точки В до прямой C₁F_.

Задача №14 по
сборнику ФИПИ 2017

Дана правильная четырёхугольная
призма ABCDA₁B₁C₁D₁.
Найдите расстояние от точки B₁ 
до плоскости AD₁
C ,
если АВ равно 5, АА₁равно 6.

Задача №14 ЕГЭ по
сборнику ФИПИ 2017

В правильной
шестиугольной призме ABCDEFA₁B₁C₁D₁
E₁F₁
все рёбра равны 4.

а) Докажите, что
угол между прямыми АD₁
и DC₁
равен 90⁰.

б) Найдите угол
между плоскостями FAC₁
 и AA₁D.

Задача №14 ЕГЭ по
сборнику ФИПИ 2017

Вывод

Мы изучили метод координат на более
высоком уровне по сравнению со школьной программой по геометрии.  Познакомились
и научились применять новые формулы: на нахождение расстояния от точки до
плоскости, от точки до прямой, угла между прямыми, угла между прямой и
плоскостью, угла между плоскостями. Мы узнали, что для
составления уравнения плоскости можно использовать матрицу и определитель
третьего порядка, который можно посчитать правилом Саррюса.

Мы
пришли к выводу, что использование метода координат требует от ученика
внимательности, хороших вычислительных навыков. Мы убеждены в том, что   координатно-векторный метод в школьном
курсе геометрии необходимо изучать на глубоком уровне и увеличить количество
часов на изучение данной темы.

 Нами
подобраны задания из сборников ФИПИ 2016г и 2017г, которые мы самостоятельно решили
и которые помогут отработать полученные навыки, и тем самым более качественно
подготовиться к сдаче экзамена.

Мы
надеемся, что изложенная в работе информация поможет выпускникам решать задание
№14 и достичь более высоких результатов на ЕГЭ по математике

Список литературы

1.     ЕГЭ
2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень

2.   ru.wikipedia.org – Система
координат.

3.   Смирнова, И.М. C50         Геометрия.
Расстояния и углы в пространстве: учебно-методическое пособие  / И.М. Смирнова,
В.А. Смирнов. – 2-е изд., перераб. И доп. – М.: Издательство «Экзамен», 2009. –
158, [2]
с.
(Серия «ЕГЭ. 100 баллов»)

4.   Геометрия, 10 – 11
: Учеб. Для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др. – 13-е изд. – М.: Просвещение, 2014. – 206 с.: ил.

5.   Корянов А.Г,
Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА
ЕГЭ 2013 (типовые задания С2) «Многогранники: виды задач
и методы их решения» www.alexlarin.narod.ru

6.   Корянов А.Г, «
Расстояния и углы в пространстве» МАТЕМАТИКА ЕГЭ 2010 (типовые задания С2) www.alexlarin.narod.ru

7.      В.В.
Леваков «Решение задач координатно-векторным методом»

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.

Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$

Подставим координаты точек в общее уравнение плоскости:

$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$

Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

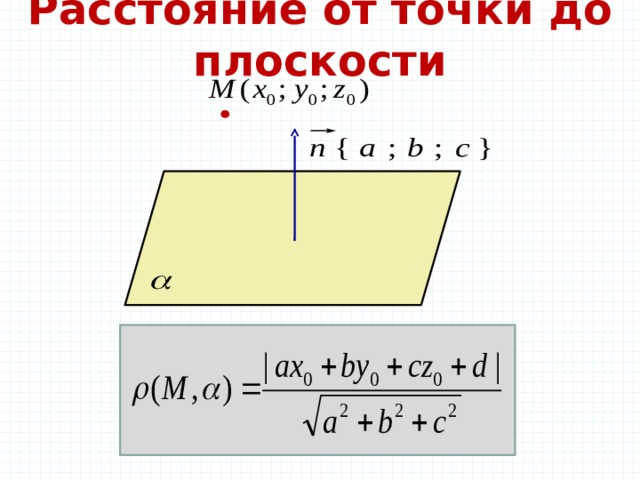
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$

Пример 4

Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).

• Докажите, что прямые (AD) и (BG) перпендикулярны.
• Найдите расстояние между прямыми (AD) и (BG).

Решение:

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

8 ноября 2020

В закладки

Обсудить

Жалоба

С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии координатно-векторным методом.

Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.

Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.

→ 14kvm.doc
→ Другое пособие по теме
→ Пособие к 14 задаче
→ Экзаменационные задачи

Стереометрия

Метод координат

в задачах № 14 ЕГЭ

Координаты точки в декартовой системе координат

Координаты вектора

=

Координаты середины отрезка

Угол между прямыми

— направляющий вектор прямой а

— направляющий вектор прямой b

— угол между прямыми

Уравнение плоскости, проходящей

через три заданных точки

-нормальный

вектор плоскости

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

-нормальный

вектор плоскости

, где

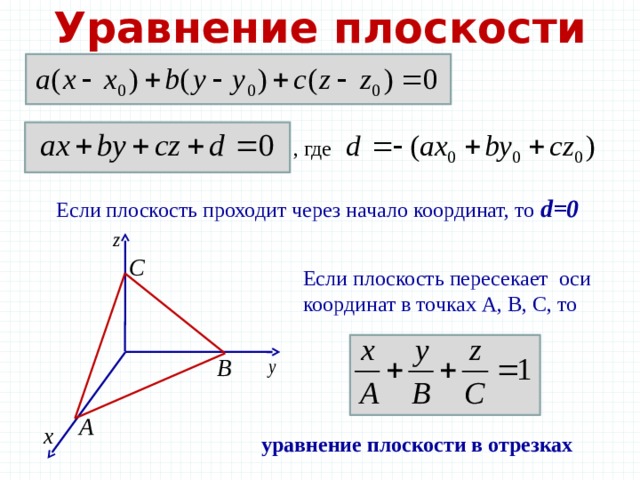
Уравнение плоскости

, где

Если плоскость проходит через начало координат, то d=0

Если плоскость пересекает оси координат в точках А, В, С, то

уравнение плоскости в отрезках

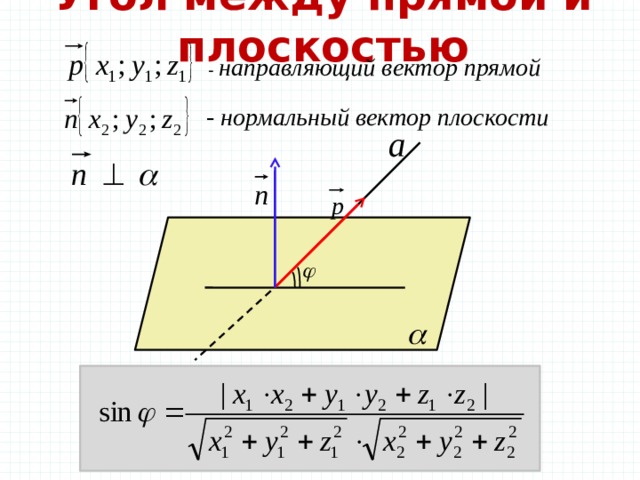
Угол между прямой и плоскостью

— направляющий вектор прямой

— нормальный вектор плоскости

Угол между плоскостями

Вектор нормали плоскости

Вектор нормали плоскости

Расстояние от точки до плоскости

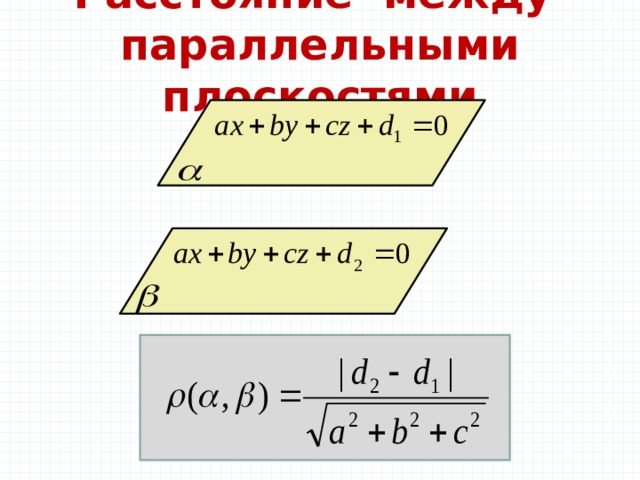
Расстояние между параллельными плоскостями

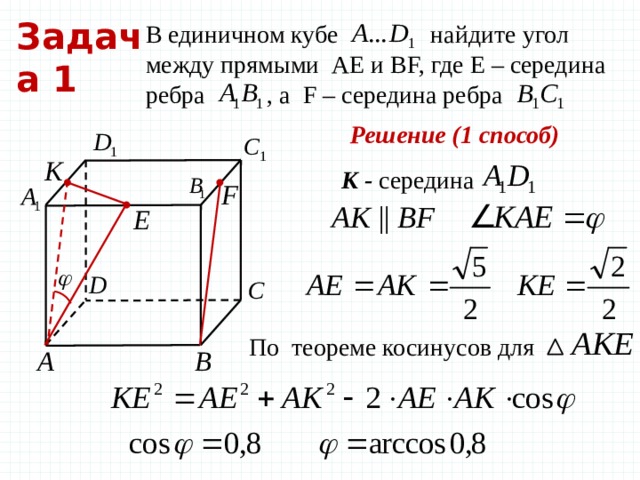
Задача 1

В единичном кубе найдите угол между прямыми AE и BF, где Е – середина ребра , а F – середина ребра

Решение (1 способ)

К — середина

По теореме косинусов для

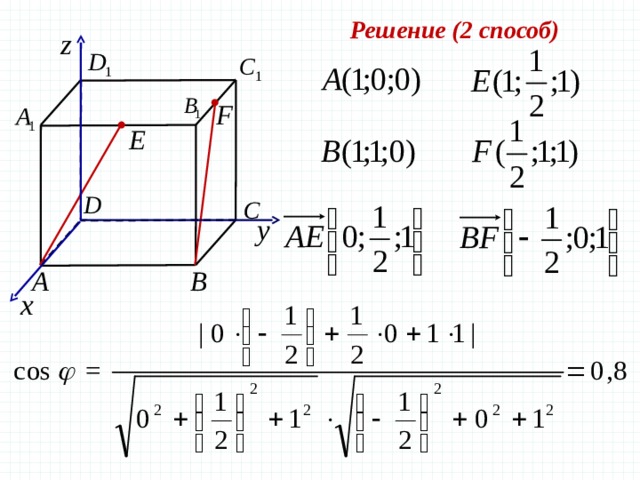
Решение (2 способ)

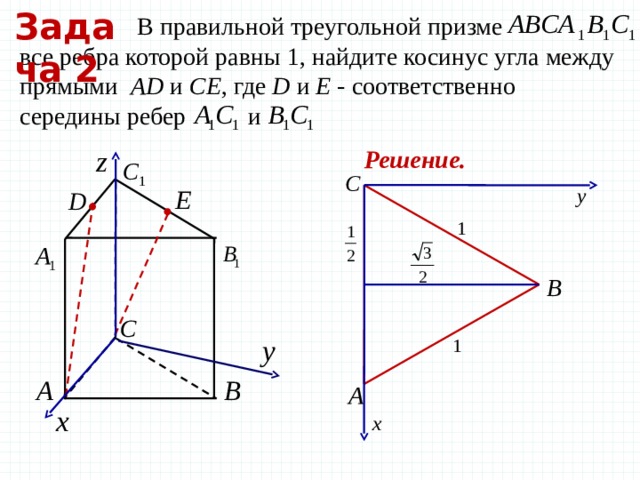
Задача 2

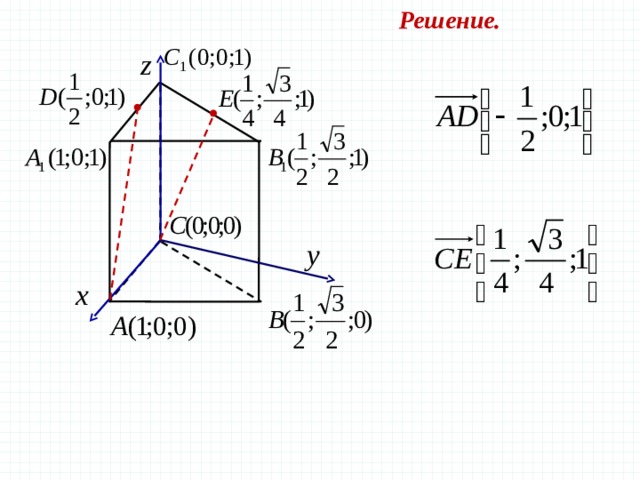
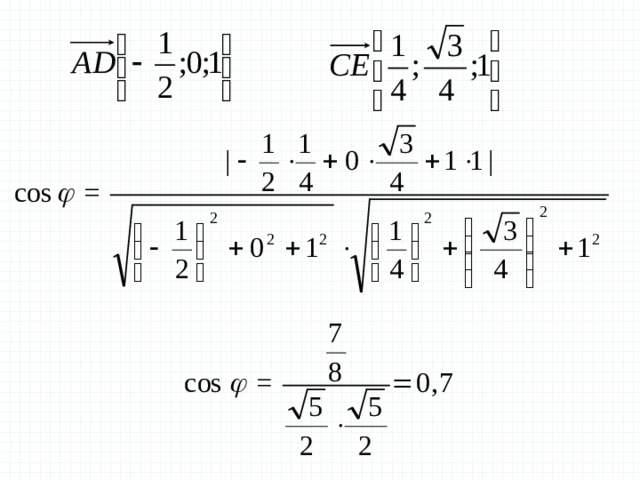
В правильной треугольной призме все ребра которой равны 1, найдите косинус угла между прямыми AD и CE , где D и E — соответственно середины ребер и

Решение.

Координаты правильной треугольной призмы

Решение.

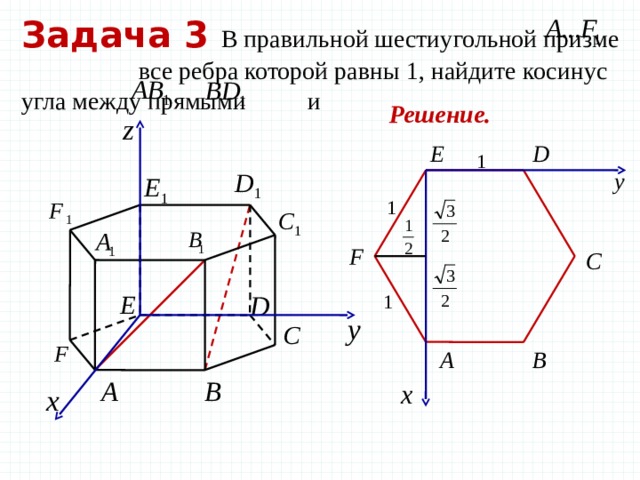
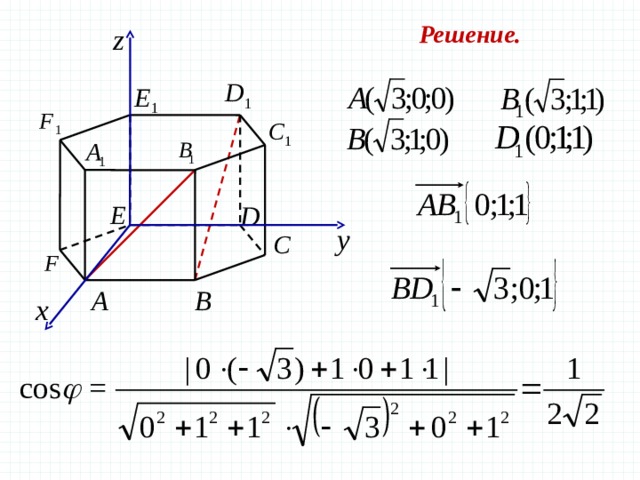
Задача 3 В правильной шестиугольной призме все ребра которой равны 1, найдите косинус угла между прямыми и

Решение.

Координаты правильной шестиугольной призмы

Решение.

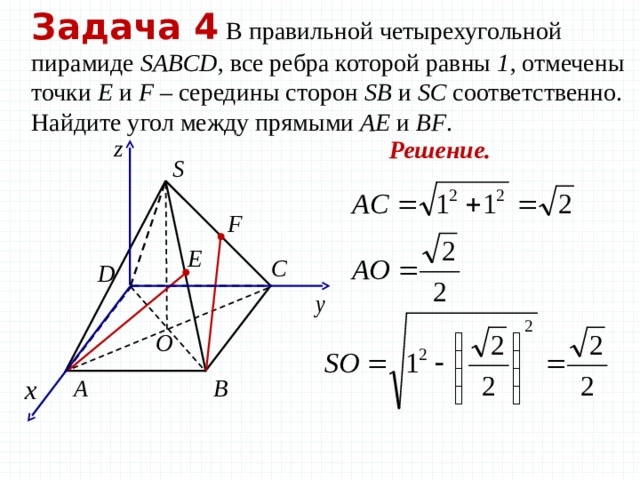
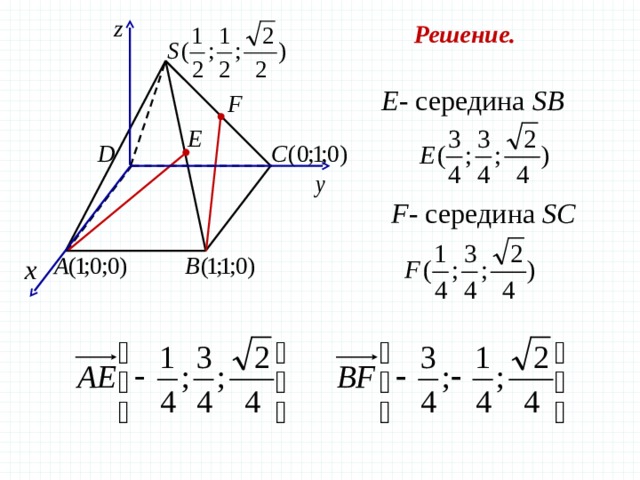
Задача 4 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF .

Решение.

Координаты правильной четырехугольной пирамиды

Решение.

Е — середина SB

F — середина SC

Задача 5 Составить уравнение плоскости, проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали.

Решение.

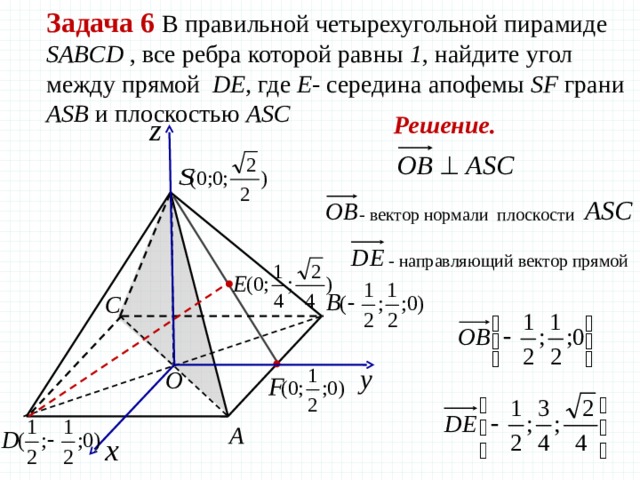
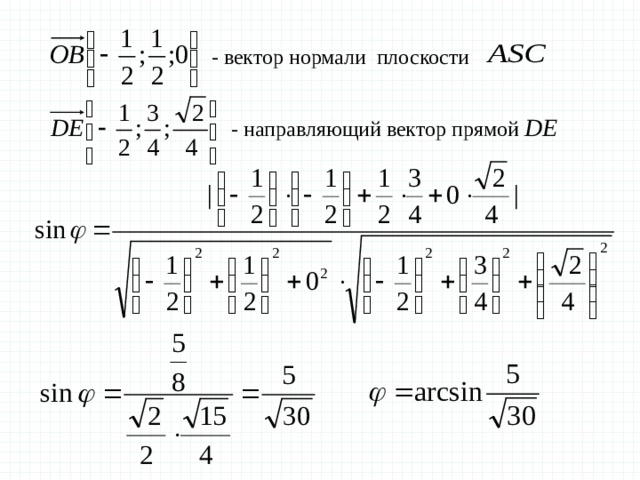
Задача 6 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите угол между прямой DE, где Е — середина апофемы SF грани ASB и плоскостью ASC

Решение.

— вектор нормали плоскости

— направляющий вектор прямой

— вектор нормали плоскости

— направляющий вектор прямой DE

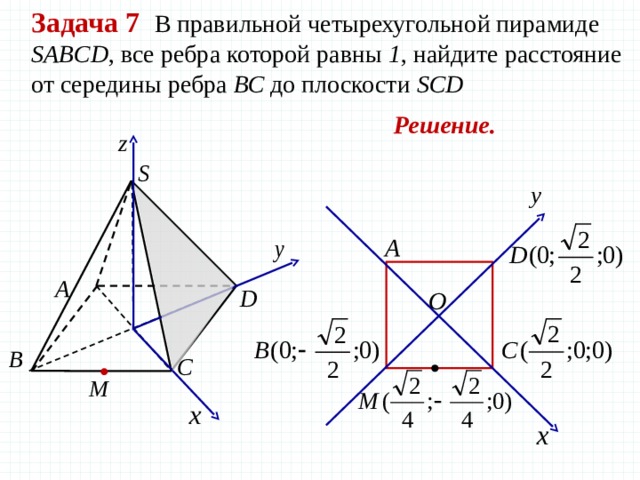
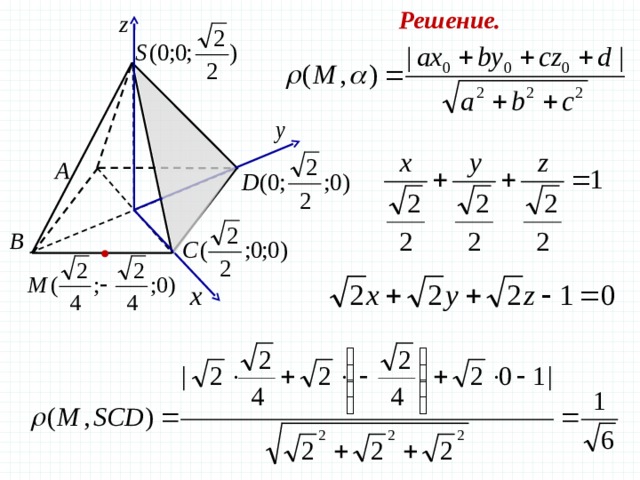
Задача 7 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1 , найдите расстояние от середины ребра ВС до плоскости SCD

Решение.

Решение.

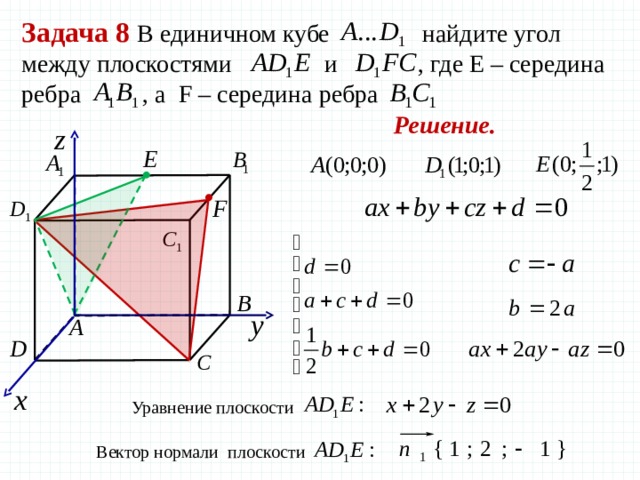
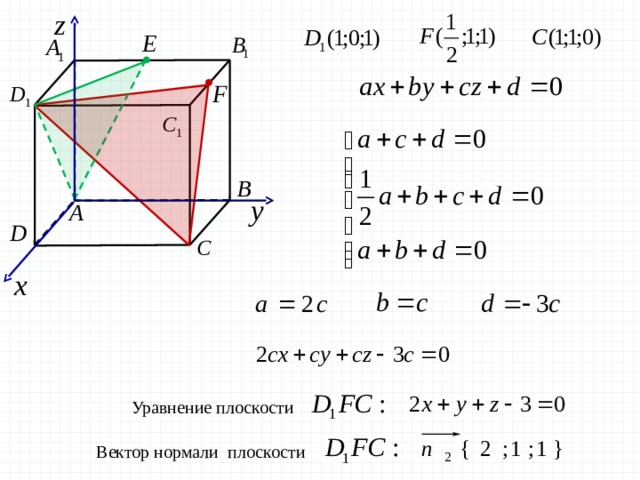
Задача 8 В единичном кубе найдите угол между плоскостями и , где Е – середина ребра , а F – середина ребра

Решение.

Уравнение плоскости

Вектор нормали плоскости

Уравнение плоскости

Вектор нормали плоскости

Задачи для самостоятельного решения

• В правильной четырёхугольной пирамиде SABCD с основанием

ABCD точка М – середина ребра SA, точка К – середина ребра SC.

Найдите угол между плоскостями МВК и АВС, если АВ=4, SC=7.

2. Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна 2√2. Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра ВC, а другая проходит через точку C и середину ребра AB.

Слайд 1

«Различные подходы к решению задач С2 в рамках Единого государственного экзамена»

Слайд 2

Содержание критерия Баллы Обосновано получен верный ответ 2 Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение не достаточно обосновано. 1 Решение не соответствует ни одному из критериев, перечисленных выше. 0 Критерии оценивания задания С2

Слайд 3

Расстояние от точки до прямой Расстояние от точки до плоскости Расстояние между скрещивающимися прямыми Угол между двумя прямыми Угол между прямой и плоскостью Угол между плоскостями Виды задач С 2:

Слайд 4

Основные методы решения задачи С 2 поэтапно-вычислительный(метод опорных задач ) (традиционный метод опирается на определения расстояния или угла, и требует от учащихся развитого пространственного воображения, применение данного метода состоит в применении известных опорных задач, которые в большинстве случаев формулируются как теоремы) метод координат (универсальный метод, может быть использован при решении задач любого вида) применение векторов (также может быть использован при решении задач любого вида) применение формул (площади ортогональной проекции многоугольника, объёма пирамиды, высоты треугольника, параллелограмма или трапеции).

Слайд 5

Расстояние от точки до прямой Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка перпендикуляра , проведенного из этой точки на прямую. Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра. Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой. a b h

Слайд 6

Расстояние от точки до прямой ( поэтапно-вычислительный метод) Задача (ЕГЭ-11г): В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 4, а боковые рёбра равны 1, найдите расстояние от точки В до прямой F 1 E 1 . Т.к. A 1 B 1 C 1 D 1 E 1 F 1 — правильный шестиугольник, то прямые В 1 F 1 и F 1 E 1 перпендикулярны, следовательно, прямые BF 1 и F 1 E 1 перпендикулярны( по ТТП). Расстояние от точки В до прямой FE 1 равно длине отрезка BF 1 . Из ∆ В 1 F 1 =4 √3 ,тогда из ∆ В F 1 B 1 : BF 1 = 7 . Ответ: 7. Решение опирается на определение расстояния :

Слайд 7

Расстояние от точки до прямой можно вычислить, как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот (по формуле) Задача: В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые рёбра равны 2 , найдите расстояние от точки F до прямой BG , где G – середина ребра SC . Решение: Искомое расстояние от точки F до прямой BG равно высоте FH треугольника FBG , в котором FB = FG = √3 ( FG – высота равностороннего треугольника SFC) . По теореме Пифагора находим Из ∆ BSC

Слайд 8

Расстояние от точки до прямой ( координатный метод) Задача: В правильной шестиугольной пирамиде SABCDEF стороны основания равны 2 , а боковые рёбра – 3. Найти расстояние от вершины S пирамиды до прямой МК, где М – середина АВ, К – середина SE. S A C O D E F x y z B М К М К S h

Слайд 9

Расстояние от точки до прямой (векторный метод) Н Задача (Тр. 4, №8): В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найти расстояние от точки В до прямой А D 1 . Решение Пусть Н – ортогональная проекция точки В на прямую AD 1.

Слайд 10

Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость. Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра. Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости. Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра. Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

Слайд 11

Расстояние от точки M до плоскости α : 1) равно расстоянию до плоскости α от произвольной точки P, лежащей на прямой l , которая проходит через точку M и параллельна плоскости α ; 2) равно расстоянию до плоскости α от произвольной точки P , лежащей на плоскости α , которая проходит через точку M и параллельна плоскости α . Расстояние от точки до плоскости α β М Р l

Слайд 12

В единичном кубе A … D 1 найдите расстояние от точки A до п лоскости BDA 1 . Ответ: Решение: Диагональ AC 1 куба перпендикулярна плоскости BDA 1 . Обозначим O — центр грани ABCD , E — точка пересечения AC 1 и плоскости BDA 1 . Длина отрезка AE будет искомым расстоянием. В прямоугольном треугольнике AOA 1 имеем AA 1 = 1; AO = ; OA 1 = . Следовательно, AE = Расстояние от точки до плоскости (поэтапно-вычислительный метод)

Слайд 13

В единичном кубе A … D 1 найдите расстояние от точки A до п лоскости CB 1 D 1 . Ответ: Решение: Плоскость CB 1 D 1 параллельна плоскости BDA 1 , и отстоит от вершины C 1 на расстояние (см. предыдущую задачу). Учитывая, что длина диагонали куба равна , получим, что искомое расстояние AF равно . Выводы: расстояние между параллельными плоскостями A 1 DВ и СВ 1 D 1 равно В кубе ABCDA 1 B 1 C 1 D 1 диагональ AC 1 перпендикулярна плоскостям A 1 B D и CB 1 D 1 и делится ими на три равные части. О Расстояние от точки С до плоскости А1 BD равно расстоянию от точки О до плоскости A1DB и равно

Слайд 14

Расстояние от точки до плоскости (поэтапно-вычислительный метод) Тр.р.№6. Задача№6 .В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, найдите расстояние между прямыми SB и AF. Решение. AF параллельна плоскости ESB , SB лежит в плоскости ESB . Задача сводится к нахождению расстояния от AF до плоскости ESB . Это есть AH ┴BE . В трапеции В AFE BE=2. AF=1,BH=1/2 . По теореме Пифагора находим AH : н Ответ:

Слайд 15

В общем случае рассматривают равенство объемов одной фигуры, выраженные двумя независимыми способами. Если объем пирамиды АВСМ равен V ABCM , то расстояние от точки M до плоскости α , содержащей треугольник АВС, вычисляют по формуле Расстояние от точки до плоскости (метод объемов)

Слайд 16

Задача (Тр. 5, №1): В единичном кубе А… D 1 найдите расстояние от точки А до плоскости С B 1 D 1 . Решение Применим формулу объёма пирамиды: Пусть АН – искомое расстояние – высота пирамиды ACB 1 D 1 . Н Расстояние от точки до плоскости (метод объемов)

Слайд 17

В правильной пирамиде SABCD , все ребра которой равны 1, н айдите расстояние от точки A до плоскости SBC . Ответ: Решение. Обозначим E , F – середины ребер AD , BC . Искомое расстояние равно высоте EH треугольника SEF , в котором SE = SF = , EF = 1. Откуда, EH = Расстояние от точки до плоскости ( по формуле )

Слайд 18

Задача (Тр. 5, №1): В единичном кубе А… D 1 найдите расстояние от точки А до плоскости С B 1 D1 . Расстояние от точки до плоскости (координатно-векторный метод ). Решение. Пусть АН – искомое расстояние АН ┴( CB 1 D 1 );Н(х;у; z) ; АН {x-1;y;z} Н х х у z (1;0;0) (0;0;1) (1;1;1) (0;1;0) АН ┴ D 1 B 1 {1 ;1;0 } АН ┴ CB 1 {1 ;1;0 } АН ┴ CH {x ; y- 1; z}

Слайд 19

Уравнение плоскости имеет вид a x + by + cz + d = 0 ,где коэффициенты – координаты вектора нормали к плоскости (вектора, перпендикулярного плоскости). A(x 1 ,y 1 ,z 1 ) C(x 3 ,y 3 ,z 3 ) M(x,y,z) B(x 2 ,y 2 ,z 2 ) Раскрыв определитель третьего порядка, получим уравнение плоскости.

Слайд 20

Расстояние от точки до плоскости (координатный метод) Задача (Тр. 5, №1): В единичном кубе А… D 1 найдите расстояние от точки А до плоскости С B 1 D 1 . Н х х у z (1;0;0) (0;0;1) (1;1;1) (0;1;0) Решение

Слайд 21

Расстояние между скрещивающимися прямыми Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра. 3) равно ρ (a;b) = ρ (A;b) , где A = a α , b = b 1 : если ортогональная проекция на плоскость α переводит прямую а в точку А, а прямую b в прямую b 1 , то расстояние между скрещивающимися прямыми а и b равно расстоянию от точки А до прямой b 1 . Расстояние между скрещивающимися прямыми 1) равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой; 2) равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые; α А α a b 1 a в α β

Слайд 22

Расстояние между скрещивающимися прямыми

Слайд 23

Расстояние между скрещивающимися прямыми (координатный метод) В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 стороны основания равны 3 и 2, а боковые рёбра равны 4. На ребре СС 1 отмечена точка К так, что СК : КС 1 = 1:3. Найти расстояние между прямыми ОК и М D, где М – середина В 1 С 1 ,О –точка пересечения диагоналей основания . 1 3 2 4 В 1 А 1 D 1 С 1 С А В D 1 z х у О (1,5;1;0) К D ( 3 ;0;0) М (0;0;2) ОК (1,5;1;1) К (3;2;1) М О Решение М D (1,5; -2 ; -4 ) М O (0; — 1; -4 )

Слайд 24

Тр.р.№6.Задача №6. В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, найдите расстояние между прямыми SB и AF. Расстояние между скрещивающимися прямым ( поэтапно-вычислительный метод ) Н Решение. AF ║BE AF ║( BSE) Задача сводится к нахождению расстояния от AF до плоскости BSE . Проведём AH ┴BE . В трапеции BAFE BE = 2, AF = 1, BH = ½ , AB = 1. Ответ:

Слайд 25

Расстояние между скрещивающимися прямыми (векторный метод) Тр.р.№6. Задача №3. В правильной треугольной призме АВСА 1 В 1 С 1 , все стороны которой равны 1, найдите расстояние между прямыми АВ и СВ 1 . F N Решение. Пусть FN – общий перпендикуляр прямых АВ и СВ 1 Введём базисные векторы: Ответ:

Слайд 26

Угол между прямыми a b — пересекающимися — скрещивающимися a b b 1

Слайд 27

• Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. • Две прямые называются перпендикулярными , если угол между ними равен 90 0 . • Угол между параллельными прямыми считается равным нулю. Угол между прямыми

Слайд 28

Задача Трапеция АВС D (AD и ВС – основания) и треугольник АЕ D лежат в разных плоскостях. МР – средняя линия ∆АЕ D . Чему равен угол между прямыми МР и АВ, если  АВС = 110 ° . А С В D E M P Ответ: 70 ° Если прямая лежит в одной из двух перпендикулярных плоскостей, то угол между прямой и плоскостью равен углу между этой прямой и линией пересечения плоскостей.

Слайд 29

Угол между прямыми (координатный метод) a b А В С D 1. A(x 1 ;y 1 ;z 1 ); B (x 2 ;y 2 ;z 2 ); Алгоритм решения: C(x 3 ;y 3 ;z 3 ); D(x 4 ;y 4 ;z 4 ).

Слайд 30

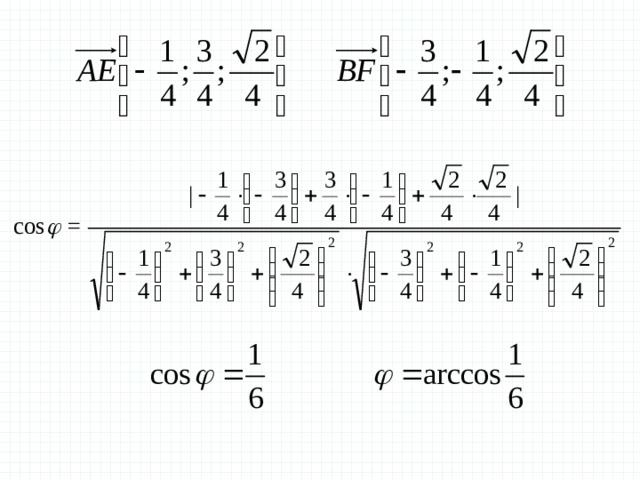
Задача . В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF. Угол между прямыми (координатный метод) Введем прямоугольную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1. Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек: у x z Решение .

Слайд 31

Угол между прямыми (координатный метод) A = (0; 0; 0); B = (1; 0; 0) Ответ : arccos (1/6) у x z Зная точки, найдем координаты направляющих векторов AE и BF: Координаты вектора AE совпадают с координатами точки E, т.к.точка A — начало координат. Найдём косинус угла:

Слайд 32

Угол между прямыми (векторный метод) Угол между прямыми считается не превосходящим 90 0 , а косинус такого угла положительным.

Слайд 33

Угол между прямыми ( векторный метод ) Задача №3диагн. р.2, В правильной шестиугольной призме A…F 1 , все рёбра которой равны 1, найдите косинус угла между прямыми AB 1 и BD 1 . Решение. Введём базисные векторы:

Слайд 34

Теорема о трех перпендикулярах: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Слайд 35

Угол между прямыми (поэтапно-вычислительный метод) Задача №1диагн. р.2, В кубе A… D 1 найдите угол между прямыми AB 1 и BD 1 . Решение. А 1 В – ортогональная проекция BD 1 на плоскость ВАА 1 . По теореме о трёх перпендикулярах: Ответ: 90 °

Слайд 36

А С В D А 1 С 1 В 1 D 1 Е F K Ответ: cos α = 0,8 Р М Угол между прямыми (поэтапно-вычислительный метод)

Слайд 37

Угол между прямой и плоскостью Углом между наклонной и плоскостью называется угол между этой наклонной и ее ортогональной проекцией на данную плоскость. Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.

Слайд 38

Угол между прямой и плоскостью

Слайд 39

Угол между прямой и плоскостью (поэтапно-вычислительный метод) Решение: Плоскость BB 1 F 1 перпендикулярна плоскости ADE 1 и пересекает ее по прямой QF 1 . В прямоугольном треугольнике QB 1 F 1 имеем: QB 1 = 2, B 1 F 1 = . Высота B 1 H этого треугольника равна . Ответ: В прямоугольном треугольнике AB 1 H имеем: AB 1 = , B 1 H = , Следовательно, В правильной 6-й призме A … F 1, ребра которой равны 1, найдите угол между прямой AB1 и плоскостью ADE 1.

Слайд 40

Угол между прямой и плоскостью (координатно-векторный метод) Задача. В правильной треугольной пирамиде ABC боковое ребро равно √3, а сторона основания равна 2√2. Найти угол между боковым ребром SA и плоскостью боковой грани SBC . Решение. Поместим пирамиду в прямоугольную систему координат так, что точка О – центр треугольника, лежащего в основании( точка пересечения медиан). z х у Уравнение плоскости SB С задаётся в виде:

Слайд 41

Угол между прямой и плоскостью (координатно-векторный метод) Задача. В правильной треугольной пирамиде DABC боковое ребро равно √3, а сторона основания равна 2√2. Найти угол между боковым ребром DA и плоскостью боковой грани DBC . Решение. Поместим пирамиду в прямоугольную систему координат так, что точка О – центр треугольника, лежащего в основании( точка пересечения медиан). z х у Уравнение плоскости SB С задаётся в виде:

Слайд 42

Угол между прямой и плоскостью (координатно-векторный метод) Уравнение плоскости принимает вид: Вектор нормали: Вектор Находим угол между данными векторами: он равен синусу угла наклона бокового ребра SA к плоскости грани SBC :

Слайд 43

Угол между прямой и плоскостью (координатно-векторный метод) Уравнение плоскости принимает вид: Вектор нормали: Вектор Находим угол между данными векторами: он равен синусу угла наклона бокового ребра DA к плоскости грани DBC :

Слайд 44

Угол между прямой и плоскостью (традиционный метод с применением формул) M T O Задача. В правильной треугольной пирамиде DABC боковое ребро равно √3, а сторона основания равна 2√2. Найти угол между боковым ребром DA и плоскостью боковой грани DBC . Решение. Сделаем некоторые дополнительные построения: Проведём АМ ┴ DT , получим, что отрезок АМ ┴ ( DBC) , и проекцией отрезка AD на плоскость (DBC) является отрезок DM. Для нахождения угла ADM дважды запишем выражения для площади треугольника ADT :

Слайд 45

Угол между прямой и плоскостью (традиционный метод с применением формул) M T O Задача. В правильной треугольной пирамиде DABC боковое ребро равно √3, а сторона основания равна 2√2. Найти угол между боковым ребром DA и плоскостью боковой грани DBC . Задачу можно решить по – другому, если заметить, что

Слайд 46

Величина двугранного угла измеряется величиной соответствующего линейного угла. Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести из этой точки луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла: Угол между двумя плоскостями (двугранный угол) равен углу между перпендикулярными к этим плоскостям прямыми. Будем считать угол между плоскостями острым (или прямым).

Слайд 47

Угол между плоскостями измеряется углом между нормалями ( n и m ) к этим плоскостям. Угол между двумя плоскостями

Слайд 48

Величиной угла между плоскостями называется величина меньшего двугранного угла. Пусть плоскости и заданы уравнениями: Косинус угла между плоскостями находится по такой формуле: В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.

Слайд 49

Задача (СтатГрад-12г). В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны единице, а боковые рёбра равны 5.На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 2:3. Найти угол между плоскостями АВС и ВЕ D 1 . Решение. Прямая D 1 Е пересекает прямую А D в точке К. Плоскости ABC и BED 1 пересекаются по прямой КВ. ЕН ┴ КВ, АН ┴КВ. Угол АНЕ – линейный угол двугранного угла между плоскостями ABC и BED 1 . EA 1 = AA 1 – AE =3. ∆ A КЕ ~ ∆ A 1 D 1 E В ∆АКВ < А=90 ° Угол между плоскостями (поэтапно-вычислительный метод)

Слайд 50

А В 1 С 1 А 1 D 1 D С В Задача (СтатГрад-12г). В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны единице, а боковые рёбра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 2:3. Найти угол между плоскостями АВС и ВЕ D 1 . 5 3 2 Е 1 1 Решение. ∆ ABD – ортогональная проекция ∆ BED 1 . Поэтому для нахождения искомого угла можно использовать формулу площади ортогональной проекции : Угол между плоскостями ( по формуле)

Слайд 51

Задача (СтатГрад-12г). В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны единице, а боковые рёбра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 2:3. Найти угол между плоскостями АВС и ВЕ D 1 . Угол между плоскостями (координатный метод) 1 3 2 5 В 1 А 1 D 1 С 1 С А В D 1 z х у (0;0;0) Е (1;0;0) (0;0;2) (1;1;0) (0;1;5) Решение. Составим уравнение каждой плоскости:

Слайд 52

Угол между плоскостями (векторный метод) Задача (СтатГрад-12г). В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны единице, а боковые рёбра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 2:3. Найти угол между плоскостями АВС и ВЕ D 1 . Решение. А В 1 С 1 А 1 D 1 D С В 5 3 2 Е 1 1 Выберем базисные векторы: 3

Слайд 53

Угол между плоскостями (векторный метод) А В 1 С 1 А 1 D 1 D С В 5 3 2 Е 1 1

Слайд 54

Информационные ресурсы Павлов А.Н. Лекции курса « Особенности методики обучения математике в условиях новой формы итоговой аттестации за курс средней школы». Смирнов В. А.. «ЕГЭ 2013. Задача С2.Геометрия. Стереометрия.» Севрюков П.Ф., Смоляков А.Н. «Векторы и координаты в решении задач школьного курса стереометрии». Корянов А.Г., Прокофьев А.А. « Типовые задания С2. Виды задач и методы их решения.» Геометрия. 10–11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].– М.: Просвещение, 2011. 2. Единый государственный экзамен 2012. Математика. Универсальные материалы для подготовки учащихся / ФИПИ– М.: Интеллект-Центр, 2012.

Метод координат… Что же это такое и зачем он нужен? Можно ли без него обойтись при сдаче ЕГЭ? Можно, безусловно! Все стереометрические задачи второй части профильного ЕГЭ по математике решаются и без привязки фигур к системе координат. Но…  координатный метод может значительно упростить решение самых сложных вопросов, таких, как определение расстояний и углов между прямыми и плоскостями в пространстве, так как там все эти расчеты сводятся, практически, к одной формуле.

       Будем разбираться!

Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у.   Это точки M(x_m; y_m)   и N(x_n; y_n)

Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении  этой системы.

Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0,       (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

Привязка фигур к  системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

  Ax + By + Cz + D = 0

 Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты  А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

Плоскость можно провести через три точки, значит, и уравнений будет три!

Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда   вместо D   будет единица, а все остальные коэффициенты будут делиться на D,  назовем их также, А, В, С. И это уже вполне решаемая система!

Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

Итак, точку описать можем, прямую описать можем, плоскость –  можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Векторы и их координаты

          Вектор – это математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой.

Мы можем «привязать» вектор к системе координат, т.е. мы можем его определять в пространстве координатами его проекций на координатные плоскости.

Если даны две точки в пространстве А(x_a; y_a; z_a) и B(x_b; y_b; z_b), то дан и вектор

, где а_х, а_у и а_z – координаты вектора.  Осталось определить значения а_х, а_у и а_z. Определяем:

а_х = x_b – x_a

а_у = y_b – y_a

а_z = z_b  –  z_а

       Теперь, зная длины проекций вектора, мы можем легко найти длину вектора, которая, как видно из чертежа, есть не что иное, как диагональ параллелепипеда, сторонами которого являются координаты этого вектора. Его длина, модуль вектора, будет равна:

А что есть длина вектора, как не расстояние между двумя точками: началом и концом вектора? То есть выведенная формула определяет расстояние между двумя точками в декартовой системе координат.

Метод координат

Примеры решения задач →