Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
2
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
3
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
4
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
5
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Пройти тестирование по этим заданиям
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Задачи на движение»
Открытый банк заданий по теме задачи на движение. Задания B11 из ЕГЭ по математике (профильный уровень)
Задание №1105
Тип задания: 11
Тема:
Задачи на движение
Условие
Два велосипедиста одновременно отправились из деревни A в деревню B, расстояние между которыми 21 км. Скорость первого велосипедиста была на 3 км/ч больше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если он приехал в деревню B на 10 мин позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго велосипедиста через x км/ч. Тогда скорость первого (x+3) км/ч, а время первого велосипедиста на прохождение всего пути frac{21}{x+3}ч, время второго велосипедиста, затраченное на прохождение всего пути frac{21}{x}ч. Разница во времени равна 10 мин = frac16часа.
Составим и решим уравнение: frac{21}{x}-frac{21}{x+3}=frac16,
6(21(x+3)-21x)=x(x+3),
x^2+3x-378=0,
x_1=18, x_2=-21.
Отрицательная скорость не удовлетворяет условию задачи. Скорость второго велосипедиста равна 18 км/ч.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1101
Тип задания: 11
Тема:
Задачи на движение
Условие
Моторная лодка прошла против течения реки 160 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше времени. Известно, что в неподвижной воде лодка движется со скоростью 15 км/ч. Найдите скорость течения реки. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость течения реки через x км/ч. Тогда скорость лодки по течению реки (15 + x) км/ч, скорость лодки против течения реки (15 — x) км/ч. Время, затраченное лодкой на путь по течению реки frac{160}{15+x} ч, время, затраченное на путь против течения реки — frac{160}{15-x} ч.
Составим и решим уравнение:
frac{160}{15-x}-frac{160}{15+x}=8,
frac{20}{15-x}-frac{20}{15+x}=1,
20(15+x-15+x)= (15-x)(15+x),
20cdot2x=225-x^2,
40x=225-x^2,
x^2+40x-225=0,
x_1=5, x_2=-45.
Скорость течения положительна, она равна 5 км/ч.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1100
Тип задания: 11
Тема:
Задачи на движение
Условие
Два мотоциклиста выехали одновременно из города A в город B, расстояние между которыми 171 км. За один час первый мотоциклист проезжает расстояние на 40 км больше второго мотоциклиста. Найдите скорость второго мотоциклиста, если он приехал в пункт В на 2,5 часа позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго мотоциклиста через x км/ч, тогда по условию скорость первого мотоциклиста (x + 40) км/ч. Время, затраченное на прохождение всего пути первым мотоциклистом, равно frac{171}{x+40} ч. Время, затраченное на прохождение всего пути вторым мотоциклистом, равно frac{171}{x} ч.
Составим и решим уравнение:
frac{171}{x}-frac{171}{x+40}=2,5,
171(x + 40) — 171x = 2,5x(x + 40),
171x+171cdot40-171x = 2,5x^2 + 100x,
2,5x^2+100x-171cdot40 =0,
x^2+40x-171cdot16=0,
x_1 = 36, x_2 = -76.
Отрицательная скорость не удовлетворяет условию. Скорость второго мотоциклиста
36 км/ч.
Ответ
36
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1096
Тип задания: 11
Тема:
Задачи на движение
Условие
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Товарный поезд имеет длину 1100 метров. Какова длина пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минуты 6 секунд. Ответ дайте в метрах.
Показать решение
Решение
Скорость пассажирского поезда относительно товарного равна 80-50=30 (км/ч) = frac{30000}{60} (м/мин) =500 (м/мин). Обозначим длину пассажирского поезда через x метров, тогда пассажирский поезд пройдёт мимо товарного поезда расстояние, равное (1100 + x) метров, за 3 мин 6 сек (3 мин 6 сек = 3,1 мин).
Составим и решим уравнение:
frac{1100+x}{3,1}=500,
1100+x=500cdot3,1,
x=1550-1100,
x=450.
Длина пассажирского поезда 450 м.
Ответ
450
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1095
Тип задания: 11
Тема:
Задачи на движение
Условие
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо семафора за 45 секунд. Найдите длину поезда в метрах.
Показать решение
Решение
Обозначим длину поезда x км. Тогда время, за которое поезд проезжает мимо семафора, равно frac{x}{60}ч. По условию это 45 секунд, то есть frac{45}{3600}ч.
frac{x}{60}=frac{45}{3600},
x=frac{60cdot45}{3600},
x=0,75 (км).
Длина поезда равна 750 м.
Ответ
750
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1094
Тип задания: 11
Тема:
Задачи на движение
Условие
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо здания вокзала, длина которого равна 150 метров, за 1 минуту. Найдите длину поезда в метрах.
Показать решение
Решение
Обозначим длину поезда x км. Длина здания равна 150 метров, то есть 0,15 км. Путь, который поезд проехал мимо здания вокзала, равен (x+0,15) км. Время, за которое поезд проезжает мимо здания вокзала, равно frac{x+0,15}{63}ч. По условию это 1 минута (1 мин = frac{1}{60} часа).
оставим и решим уравнение: frac{x+0,15}{63}=frac{1}{60},
x=0,9 (км).
Длина поезда равна 900 м.
Ответ
900
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1093
Тип задания: 11
Тема:
Задачи на движение
Условие
Из двух посёлков, расстояние между которыми 88 км, навстречу друг другу одновременно выехали два велосипедиста. Через сколько часов велосипедисты встретятся, если их скорости равны 18 км/ч и 22 км/ч?
Показать решение
Решение
Обозначим время велосипедистов до встречи через x ч. Тогда первый велосипедист до встречи проедет 18x км, а второй велосипедист проедет до встречи 22x км.
Составим и решим уравнение:
8x + 22x = 88, 40x = 88, x = 2,2.
Велосипедисты встретятся через 2,2 часа.
Ответ
2,2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №945
Тип задания: 11
Тема:
Задачи на движение
Условие
Теплоход проходит по течению реки до пункта назначения 221 км и после стоянки возвращается в пункт отправления. Скорость движения теплохода в воде без течения равна 15 км/ч. Стоянка длилась 7 часов. Найдите скорость течения реки, если в пункт отправления теплоход вернулся через 37 часов после отплытия из него. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость течения через x км/ч, тогда скорость теплохода по течению реки равна (15+x) км/ч, скорость теплохода против течения (15-x) км/ч. Время движения теплохода равно 37-7=30 ч.
Составим и решим уравнение:
frac{221}{15+x}+frac{221}{15-x}=30,
221(15-x+15+x)=30(15-x)(15+x),
221=225-x^2,
x^2=4,
x_1=2,,x_2=-2.
Скорость течения положительна, она равна 2 км/ч.
Ответ
2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №944
Тип задания: 11
Тема:
Задачи на движение
Условие
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми 288 км. На следующий день он поехал обратно со скоростью на 6 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 4 часа. В итоге на возвращение в город A у него ушло сколько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость велосипедиста на пути от A до B через x км/ч, x>0. Тогда его скорость на обратном пути будет (x+6) км/ч. Время, затраченное велосипедистом на путь от A до B, равно frac{288}{x}ч, время движения на обратном пути frac{288}{x+6}ч.
Составим и решим уравнение:
frac{288}{x}-frac{288}{x+6}=4,
288(x+6-x)=4x(x+6),
72cdot6=x^2+6x,
x^2+6x-432=0,
x_1=18,,x_2=-24.
Отрицательная скорость не удовлетворяет условию задачи. Скорость велосипедиста равна 18 км/ч.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №943
Тип задания: 11
Тема:
Задачи на движение
Условие
Из пункта A в пункт B одновременно выехали две дорожные машины. Первая машина проехала с постоянной скоростью весь путь. Вторая проехала первую половину пути со скоростью 39 км/ч, а вторую половину пути — со скоростью на 26 км/ч большей скорости первой машины, в результате чего в пункт B обе машины прибыли одновременно. Найдите скорость первой машины. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость первой машины через x км/ч, путь от A до B s км, тогда путь от пункта A в пункт B она пройдёт за frac sxч. Половина пути пройдена второй машиной со скоростью 39 км/ч за frac{0,5s}{39}=frac{s}{78}ч. Скорость второй машины на второй половине пути равна (x+26) км/ч, таким образом, время, затраченное на вторую половину пути второй машиной, равно frac{0,5s}{x+26}ч.
Составим и решим уравнение:
frac sx=frac{s}{78}+frac{0,5s}{x+26},
frac 2x=frac{2}{78}+frac{1}{x+26},
frac 2x-frac{1}{39}-frac{1}{x+26}=0,
frac{2cdot39(x+26)-x(x+26)-39x}{39x(x+26)}=0,
78x+39cdot52-x^2-26x-39x=0,
x^2-13x-39cdot52=0,
x_1=52,,x_2=-39.
Отрицательная скорость не удовлетворяет условию. Скорость первой машины 52 км/ч.
Ответ
52
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
На чтение 9 мин Просмотров 18.3к. Опубликовано 16 ноября, 2020
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Содержание
- Как решать задачи на движение
- Примеры решения
- Виды задач на движение
- Движение навстречу друг другу, движение в противоположных направлениях
- Движение друг за другом (вдогонку)
- Задачи на движение по кругу
- Задачи на движение мимо объекта
- Задачи на движение по течению и против течения
- Задачи на движение из ЕГЭ по математике (профильный уровень)
- Задача 1.
- Задача 2.
- Задача 3
- Задача 4
- Задача 5
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение
Движение навстречу друг другу, движение в противоположных направлениях
Если два объекта движутся навстречу друг другу, то они сближаются:
При движении в противоположном направлении объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Таким образом:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
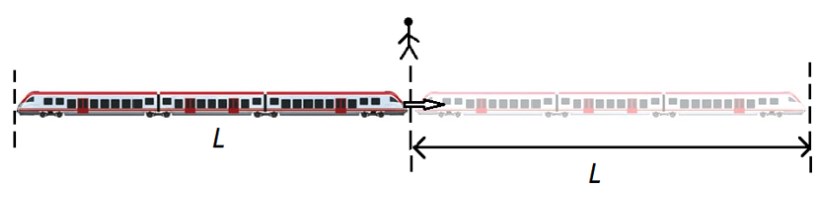
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ = v ∙
= v ∙
+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
1 ед.отн. = 20
6 ед.отн. = 120
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда
, отсюда
и
.
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ больше, чем x ∙
больше, чем x ∙
на 14.
80 ∙ = x ∙
= x ∙
+ 14;
–
–
= x ∙
;
160 – 42 = х ∙ 2;
х = 59.
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10 км/ч.
ЕГЭ Профиль №9. Задачи на движение по прямой
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на движение по прямой
|
Задача 1. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. Пусть x км/ч – скорость первого автомобиля, тогда скорость второго на второй половине пути равна x + 16 км/ч. Возьмём расстояние между пунктами за 2 S км.
Автомобили были в пути одно и то же время. Следовательно: (frac{S}{{24}} + frac{S}{{x + 16}} = frac{{2S}}{x},,left| {,:,S ne 0,,,,, Leftrightarrow ,,,,,} right.frac{1}{{24}} + frac{1}{{x + 16}} = frac{2}{x},,,, Leftrightarrow ,,,,,frac{{x + 16 + 24}}{{24left( {x + 16} right)}} = frac{2}{x},,,,, Leftrightarrow ) ( Leftrightarrow ,,,,xleft( {x + 40} right) = 48left( {x + 16} right),,,, Leftrightarrow ,,,,{x^2} — 8x — 768 = 0) (D = 64 + 3072 = 3136;,,,,,{x_1} = frac{{8 + 56}}{2} = 32;,,,,{x_2} = frac{{8 — 56}}{2} = — 24.) Так как (x > 0), то скорость первого автомобиля равна 32 км/ч. Ответ: 32. |
||||||||||||||||||||||||
| Задача 2. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Пусть x км/ч – скорость первого автомобиля, тогда скорость второго на первой половине пути равна x – 13 км/ч. Возьмём расстояние между пунктами за 2 S км.
Автомобили были в пути одно и то же время. Следовательно: (frac{S}{{x — 13}} + frac{S}{{78}} = frac{{2S}}{x},,left| {,:,S ne 0,,,,, Leftrightarrow ,,,,,} right.frac{1}{{x — 13}} + frac{1}{{78}} = frac{2}{x},,,, Leftrightarrow ,,,,,frac{{78 + x — 13}}{{78left( {x — 13} right)}} = frac{2}{x},,,,, Leftrightarrow ) ( Leftrightarrow ,,,,xleft( {x + 65} right) = 156left( {x — 13} right),,,, Leftrightarrow ,,,,{x^2} — 91x + 13 cdot 156 = 0) (D = {91^2} — 4 cdot 13 cdot 156 = {13^2} cdot {7^2} — 4 cdot {13^2} cdot 12 = {13^2}left( {49 — 48} right) = {13^2};,,,,,{x_1} = frac{{91 + 13}}{2} = 52;,,,,{x_2} = frac{{91 — 13}}{2} = 39.) Так как по условию задачи (x > 48), то скорость первого автомобиля равна 52 км/ч. Ответ: 52. |
||||||||||||||||||||||||
| Задача 3. Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста, тогда скорость автомобиля равна x + 40 км/ч.
Так как, велосипедист прибыл в пункт В на 6 часов позже автомобилиста, то его время на 6 часов больше. Следовательно: (frac{{75}}{x} — frac{{75}}{{x + 40}} = 6,,,,,, Leftrightarrow ,,,,,frac{{75left( {x + 40} right) — 75x}}{{xleft( {x + 40} right)}} = 6,,, Leftrightarrow ,,,,,frac{{75 cdot 40}}{{xleft( {x + 40} right)}} = 6,,,, Leftrightarrow ,,,,6xleft( {x + 40} right) = 75 cdot 40,,left| {,:6,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,{x^2} + 40x — 500 = 0;,,,,D = 1600 + 2000 = 3600;,,,,{x_1} = frac{{ — 40 + 60}}{2} = 10;,,,,{x_2} = frac{{ — 40 — 60}}{2} = — 50) Так как (x > 0), то скорость велосипедиста равна 10 км/ч. Ответ: 10. |
||||||||||||||||||||||||
| Задача 4. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста из В в А, тогда его скорость из А в В равна x – 3 км/ч.
Так как, на обратном пути велосипедист сделал остановку на 3 часа и в результате затратил столько же времени, то: (frac{{70}}{{x — 3}} — frac{{70}}{x} = 3,,,,,, Leftrightarrow ,,,,,frac{{70x — 70left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 3,, Leftrightarrow ,,,,,frac{{70 cdot 3}}{{xleft( {x — 3} right)}} = 3,,,, Leftrightarrow ,,,,3xleft( {x — 3} right) = 70 cdot 3,,,, Leftrightarrow ) ( Leftrightarrow ,,,{x^2} — 3x — 70 = 0;,,,,D = 9 + 280 = 289;,,,,{x_1} = frac{{3 + 17}}{2} = 10;,,,,{x_2} = frac{{3 — 17}}{2} = — 7) Так как (x > 0), то скорость велосипедиста из В в А равна 10 км/ч. Ответ: 10. |
||||||||||||||||||||||||
| Задача 5. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста из А в В, тогда его скорость из В в А равна x + 7 км/ч.
Так как, на обратном пути велосипедист делал остановку на 7 часов и в результате затратил столько же времени, то: (frac{{98}}{x} — frac{{98}}{{x + 7}} = 7,,,,,, Leftrightarrow ,,,,,frac{{98left( {x + 7} right) — 98x}}{{xleft( {x + 7} right)}} = 7,, Leftrightarrow ,,,,,frac{{98 cdot 7}}{{xleft( {x + 7} right)}} = 7,,,, Leftrightarrow ,,,,7xleft( {x + 7} right) = 98 cdot 7,,, Leftrightarrow ) ( Leftrightarrow ,,,{x^2} + 7x — 98 = 0;,,,,D = 49 + 392 = 441;,,,,{x_1} = frac{{ — 7 + 21}}{2} = 7;,,,,{x_2} = frac{{ — 7 — 21}}{2} = — 14) Так как (x > 0), то скорость велосипедиста из А в В равна 7 км/ч. Ответ: 7. |
||||||||||||||||||||||||
|
Задача 6. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч. Пусть x км/ч – скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста x – 1 км/ч.
Так как первый велосипедист приехал на 1 час раньше второго, то его время на 1 час меньше. Следовательно: (frac{{240}}{{x — 1}} — frac{{240}}{x} = 1,,,,,, Leftrightarrow ,,,,,frac{{240x — 240left( {x — 1} right)}}{{xleft( {x — 1} right)}} = 1,,,,, Leftrightarrow ,,,,,frac{{240}}{{xleft( {x — 1} right)}} = 1,,,, Leftrightarrow ,,,,xleft( {x — 1} right) = 240,,, Leftrightarrow )( Leftrightarrow ,,,,,{x^2} — x — 240 = 0;,,,,,D = 1 + 4 cdot 240 = 961;,,,,,{x_1} = frac{{1 + 31}}{2} = 16;,,,,,{x_2} = frac{{1 — 31}}{2} = — 15.) Так как (x > 0), то скорость велосипедиста, пришедшего к финишу первым, равна 16 км/ч. Ответ: 16. |
||||||||||||||||||||||||
| Задача 7. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Пусть t ч – время движения автомобилей до встречи. Тогда первый автомобиль пройдет расстояние – 65t км, а второй – 75t км. Следовательно: (65t + 75t = 560,,,, Leftrightarrow ,,,,140t = 560,,,, Leftrightarrow ,,,,t = 4). Таким образом, автомобили встретятся через 4 часа. Ответ: 4. |
||||||||||||||||||||||||
| Задача 8. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Так как автомобили встретились на расстоянии 180 км от города В, то автомобиль, выехавший из города А, проехал расстояние (330 — 180 = 150) км за 3 часа. Следовательно, его скорость равна: (V = frac{{150}}{3} = 50) км/ч. Ответ: 50. |
||||||||||||||||||||||||
| Задача 9. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Пусть t ч – время движения до встречи автомобиля, выехавшего из города А, тогда время второго автомобиля t – 1 ч. За t часов первый автомобиль проехал расстояние 60t км, а второй за t – 1 ч проехал 65(t – 1), а вместе до встречи они проехали 435 км. Следовательно: (60t + 65left( {t — 1} right) = 435,,,,, Leftrightarrow ,,,,,60t + 65t — 65 = 435,,,,, Leftrightarrow ,,,,125,t = 500,,,,, Leftrightarrow ,,,,,t = 4.) Следовательно, первый проехал расстояние (60 cdot 4 = 240) км, и оно равно расстоянию от города А до встречи автомобилей. |
||||||||||||||||||||||||
| Задача 10. Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
Автомобиль, выехавший из города В со скоростью 60 км/ч, проехал расстояние (470 — 350 = 120) км. Следовательно, он затратил на этот путь время равное: (frac{{120}}{{60}} = 2) часа. Тогда автомобиль, выехавший из города А, затратил на расстояние равное 350 км время равное: (2 + 3 = 5) часов. Поэтому его скорость равна: (frac{{350}}{5} = 70) км/ч. Ответ: 70. |
||||||||||||||||||||||||
| Задача 11. Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Пусть время движения велосипедиста из В в А равно x ч, тогда время движения мотоциклиста из А в В равно x – 3 ч, при этом (x — 3 > 0), то есть (x > 3). Обозначим расстояние между городами за S км. Тогда скорость велосипедиста равна: (frac{S}{x}), а скорость мотоциклиста (frac{S}{{x — 3}}). За время 48 минут ((frac{{48}}{{60}} = frac{4}{5}) ч) велосипедист проехал расстояние: (frac{4}{5} cdot frac{S}{x}) км, а мотоциклист: (frac{4}{5} cdot frac{S}{{x — 3}}) км, а вместе они преодолели расстояние равное S км. Следовательно: (frac{4}{5} cdot frac{S}{x} + frac{4}{5} cdot frac{S}{{x — 3}} = S,,left| : right.,,S ne 0,,,,, Leftrightarrow ,,,,,frac{4}{{5x}} + frac{4}{{5left( {x — 3} right)}} = 1,,,,, Leftrightarrow ,,,,,frac{{4left( {x — 3} right) + 4x}}{{5xleft( {x — 3} right)}} = 1,,,, Leftrightarrow ) ( Leftrightarrow ,,,,5{x^2} — 15x = 8x — 12,,,, Leftrightarrow ,,,,5{x^2} — 23x + 12 = 0;) (D = 529 — 240 = 289;,,,,{x_1} = frac{{23 + 17}}{{10}} = 4;,,,,{x_2} = frac{{23 — 17}}{{10}} = frac{3}{5}.) Так как (x > 3), то время велосипедиста их В в А равно 4 часа. Ответ: 4. |
||||||||||||||||||||||||
| Задача 12. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Пусть x км/ч – скорость товарного поезда, тогда скорость скорого x км/ч +750 м/мин = (x + frac{{750}}{{1000}} cdot 60 = x + 45) км/ч.
По условию задачи время товарного поезда на 2 часа больше. Следовательно: (frac{{180}}{x} — frac{{180}}{{x + 45}} = 2,,,,,, Leftrightarrow ,,,,,frac{{180left( {x + 45} right) — 180x}}{{xleft( {x + 45} right)}} = 2,, Leftrightarrow ,,,,,frac{{180 cdot 45}}{{xleft( {x + 45} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 45} right) = 180 cdot 45,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 45 — 90 cdot 45 = 0) (D = {45^2} + 4 cdot 90 cdot 45 = {45^2}left( {1 + 4 cdot 2} right) = {45^2} cdot 9;,,,,,,sqrt D = ,,45 cdot 3 = 135;) (,,,{x_1} = frac{{ — 45 + 135}}{2} = 45;,,,,{x_2} = frac{{ — 45 — 135}}{2} = — 90.) Так как (x > 0), то скорость товарного поезда равна 45 км/ч. Ответ: 45. |
||||||||||||||||||||||||
| Задача 13. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть x км – расстояние от А до С, а y км/ч – скорость автомобиля. Рассмотрим сначала движение автомобиля и мотоцикла от А до С.
Так как автомобиль выехал на 30 мин раньше, то его время на (frac{1}{2}) часа больше. Тогда первое уравнение будет иметь вид: (frac{x}{y} — frac{x}{{90}} = frac{1}{2}.) Теперь рассмотрим случай движения автомобиля из С в В, а мотоциклиста из С в А.
Так как мотоциклист вернулся в А одновременно с автомобилистом, приехавшим в В, то второе уравнение будет иметь вид: (frac{{150 — x}}{y} = frac{x}{{90}}.) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{x}{y} — frac{x}{{90}} = frac{1}{2};} \ {frac{{150 — x}}{y} = frac{x}{{90}}.} end{array}} right.) Из второго уравнения: (y = frac{{90left( {150 — x} right)}}{x}) подставляя в первое уравнение, получим: (frac{{{x^2}}}{{90left( {150 — x} right)}} — frac{x}{{90}} = frac{1}{2},,,,,, Leftrightarrow ,,,,,,frac{{{x^2} — xleft( {150 — x} right)}}{{90left( {150 — x} right)}} = frac{1}{2},,,,,, Leftrightarrow ,,,,,,frac{{2{x^2} — 150x}}{{90left( {150 — x} right)}} = frac{1}{2},,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,4{x^2} — 300x = 90 cdot 150 — 90x,,left| {,:,2,,,,, Leftrightarrow ,,,,2{x^2} — 105x — 6750 = 0} right.;) (D = {105^2} + 4 cdot 2 cdot 6750 = {15^2} cdot {7^2} + 4 cdot 2 cdot {15^2} cdot 30 = {15^2}left( {49 + 240} right) = {15^2} cdot 289;,,,) (sqrt D = 15 cdot 17 = 255;,,,,,{x_1} = frac{{105 + 255}}{4} = 90;,,,,,{x_2} = frac{{105 — 255}}{4} = — 37,5.) Так как (x > 0), то расстояние от А до С равно 90 км. Ответ: 90. |
| Задача 14. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Пусть x км/ч – скорость второго пешехода, тогда x + 1,5 км/ч – скорость первого, а в пути они были t ч.
Так как расстояние между пешеходами должно стать равно 300 м = 0,3 км, то первый должен пройти на 0,3 км больше. Следовательно: (left( {x + 1,5} right)t — x,t = 0,3,,,,,, Leftrightarrow ,,,,,x,t + 1,5,t — x,t = 0,3,, Leftrightarrow ,,,,,1,5t = 0,3,,,, Leftrightarrow ,,,,t = frac{1}{5},.,,) Следовательно, через (frac{1}{5}) часа или (frac{1}{5} cdot 60 = 12) минут расстояние между пешеходами будет ровно 300 м. Ответ: 12. Второй вариант решения: Так как скорость первого пешехода на 1,5 км/ч больше скорости второго, то через 1 час (60 минут) расстояние между пешеходами будет равно 1,5 км (1500 м). Следовательно, чтобы расстояние между пешеходами стало равно 300 м (это в 5 раз меньше чем 1500 м) понадобиться 12 минут (это в 5 раз меньше чем 60 минут). Ответ: 12. |
||||||||||||
| Задача 15. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, которое ему понадобилось, чтобы догнать второго велосипедиста. Тогда за время t ч третий проехал расстояние равное (x cdot t) км, а второй выехал на 1 час раньше третьего, поэтому он проехал расстояние (10left( {t + 1} right)) км. Следовательно, первое уравнение будет иметь вид: (x cdot t = 10left( {t + 1} right)). Теперь рассмотрим, как третий велосипедист догоняет первого. Третьему велосипедисту понадобилось t ч, чтобы догнать второго, а затем еще 2 часа 20 минут, чтобы догнать первого, то есть третий догонял первого (t + frac{7}{3}) часа и проехал расстояние: (x cdot left( {t + frac{7}{3}} right)). Первый выехал на 2 часа раньше третьего, поэтому он проехал расстояние равное: (15 cdot left( {t + frac{7}{3} + 2} right)). Следовательно, второе уравнение будет иметь вид: (xleft( {t + frac{7}{3}} right) = 15left( {t + frac{{13}}{3}} right)). Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {x cdot t = 10left( {t + 1} right);,,,,,,,,,,,,,,,,,,,,} \ {x cdot left( {t + frac{7}{3}} right) = 15left( {t + frac{{13}}{3}} right).} end{array}} right.) Из первого уравнения: (x = frac{{10left( {t + 1} right)}}{t}). Подставляя во второе первое, получим: (frac{{10t + 10}}{t} cdot frac{{3t + 7}}{3} = 15t + 65,,,, Leftrightarrow ,,,,30{t^2} + 70t + 30t + 70 = 45{t^2} + 195t,,,, Leftrightarrow ) ( Leftrightarrow ,,,,15{t^2} + 95t — 70 = 0,,left| {,:} right.5,,,, Leftrightarrow ,,,,3{t^2} + 19t — 14 = 0;) (D = 361 + 168 = 529;,,,,{t_1}, = frac{{ — 19 + 23}}{6} = frac{2}{3};,,,,{t_2} = frac{{ — 19 — 23}}{6} = — 7) Так как, (t > 0), то (t = frac{2}{3}) часа. Следовательно, скорость третьего велосипедиста: (x = frac{{10 cdot left( {frac{2}{3} + 1} right)}}{{frac{2}{3}}} = 25) км/ч. ()Ответ: 25. |
||||||||||||
| Задача 16. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть автомобиль находился в пути 2t часов. Тогда за первую половину времени (то есть за t часов) он проехал расстояние равное 74t км, а за вторую половину 66t км. Тогда средняя скорость автомобиля будет равна: (V = frac{{74t + 66t}}{{2t}} = frac{{140t}}{{2t}} = 70) км/ч. Ответ: 70. |
||||||||||||
| Задача 17. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть путешественник проплыл расстояние на яхте равное S км, тогда его время на яхте составило ({t_1} = frac{S}{{20}}) ч, а на самолете ({t_2} = frac{S}{{480}}) ч. Тогда средняя скорость будет равна: (v = frac{{S + S}}{{{t_1} + {t_2}}} = frac{{2S}}{{frac{S}{{20}} + frac{S}{{480}}}} = frac{{2S}}{{frac{{24S + S}}{{480}}}} = frac{{2S cdot 480}}{{25,S}} = 38,4) км/ч. Ответ: 38,4. |
||||||||||||
| Задача 18. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть 3S км – весь путь автомобиля, тогда его время на первом участке ({t_1} = frac{S}{{60}}), на втором ({t_2} = frac{S}{{120}}), а на третьем ({t_3} = frac{S}{{110}}). Тогда средняя скорость будет равна: (V = frac{{S + S + S}}{{{t_1} + {t_2} + {t_3}}} = frac{{3S}}{{frac{S}{{60}} + frac{S}{{120}} + frac{S}{{110}}}} = frac{{3S}}{{frac{{2S + S}}{{120}} + frac{S}{{110}}}} = frac{{3S}}{{frac{S}{{40}} + frac{S}{{110}}}} = frac{{3S}}{{frac{{11S + 4S}}{{440}}}} = frac{{3S cdot 440}}{{15S}} = 88) км/ч. Ответ: 88. |
||||||||||||
| Задача 19. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Автомобиль был в пути время равное (2 + 1 + 2 = 5) часов и проехал за это время расстояние равное (2 cdot 50 + 1 cdot 100 + 2 cdot 75 = 350) км. Тогда его средняя скорость: (V = frac{{350}}{5} = 70) км/ч. Ответ: 70. |
||||||||||||
| Задача 20. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Первые 190 км автомобиль проехал за время ({t_1} = frac{{190}}{{50}} = frac{{19}}{5}) часа, следующие 180 км за ({t_2} = frac{{180}}{{90}} = 2) часа, а последние 170 км за ({t_3} = frac{{170}}{{100}} = frac{{17}}{{10}}) часа. Таким образом, он проехал расстояние равное (190 + 180 + 170 = 540) км за время ({t_{}} = frac{{19}}{5} + 2 + frac{{17}}{{10}} = frac{{15}}{2}) часа. Следовательно, его средняя скорость равна: (V = frac{{540}}{{frac{{15}}{2}}} = 72) км/ч. Ответ: 72. |
||||||||||||
| Задача 21. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Проезжая мимо столба, поезд проезжает расстояние равное своей длине, то есть длина поезда равна расстоянию, которое проехал поезд. (t = 36) с ( = frac{{36}}{{3600}}) ч ( = frac{1}{{100}}) ч. (S = V cdot t = 80 cdot frac{1}{{100}} = 0,8) км. Следовательно, длина поезда равна 0,8 км = 800 м. Ответ: 800. |
||||||||||||
| Задача 22. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Проезжая мимо лесополосы, поезд проезжает расстояние равное сумме длин лесополосы и самого поезда, то есть длина поезда равна расстоянию, которое проехал поезд минус длина лесополосы. (t = 1) мин ( = frac{1}{{60}}) ч. (S = V cdot t = 60 cdot frac{1}{{60}} = 1) км. Следовательно, поезд проехал расстояние равное 1000 м, тогда длина поезда (1000 — 400 = 600) м. Ответ: 600. |
||||||||||||
| Задача 23. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Так как поезда едут в одном направлении, то их скорость сближения равна (V = 90 — 30 = 60) км/ч. Следовательно, за 1 минуту пассажирский поезд сместится относительно товарного на 1 км. При этом он преодолеет расстояние равное сумме длин поездов. Поэтому длина пассажирского поезда равна (1000 — 600 = 400) м. Ответ: 400. |
||||||||||||
| Задача 24. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Так как поезда едут навстречу друг другу, то их скорость сближения равна (V = 65 + 35 = 100) км/ч. За 36 секунд скорый поезд сместится относительно пассажирского на расстояние: (S = 100 cdot frac{{36}}{{3600}} = 1) км. При этом он преодолел расстояние равное сумме длин поездов. Поэтому длина скорого поезда равна (1000 — 700 = 300)м. Ответ: 300. |
||||||||||||
| Задача 25. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Пусть x км – расстояние, которое не дошел до опушки первый человек, оно равно расстоянию, которое прошел от опушки до места встречи второй человек. Следовательно, первый прошел расстояние равное (4,4 — x) км, а второй (4,4 + x).
Путники затратили одно и тоже время: (frac{{4,4 — x}}{{2,5}} = frac{{4,4 + x}}{3},,,,,, Leftrightarrow ,,,,,4,4 cdot 3 — 3x = 2,5 cdot 4,4 + 2,5x,, Leftrightarrow ,,,,,5,5x = 4,4 cdot 3 — 2,5 cdot 4,4,,,, Leftrightarrow ,,,)( Leftrightarrow ,,,,5,5x = 4,4left( {3 — 2,5} right),,,, Leftrightarrow ,,,,5,5 = 4,4 cdot 0,5,,,, Leftrightarrow ,,,,x = frac{{4,4 cdot 0,5}}{{5,5}} = 0,4). Следовательно, встреча произойдет от точки отправления на расстоянии (4,4 — 0,4 = 4) км. Ответ: 4. |
||||||||||||
| Задача 26. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?
Пусть x км/ч – скорость туриста на спуске, тогда скорость на подъёме (x — 3) км/ч. Время на подъёме: (5 — 1 = 4) часа.
Так как весь путь равен 8 км, то: (4left( {x — 3} right), + x = 8,,,,, Leftrightarrow ,,,,,5x = 20,,,,, Leftrightarrow ,,,,,x = 4) км/ч. Ответ: 4. |
||||||||||||
| Задача 27. Иван и Алексей договорились встретиться в N-ске. Иван звонит Алексею и узнаёт, что тот находится в 275 км от N-ска и едет с постоянной скоростью 75 км/ч. Иван в момент разговора находится в 255 км от N-ска и ещё должен по дороге сделать 50-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем?
Пусть x км/ч – скорость Ивана.
Поскольку Иван должен сделать 50 – минутную остановку, то его время движения будет на (frac{5}{6}) часа меньше. (frac{{275}}{{75}} — frac{{255}}{x} = frac{5}{6},,,,,,, Leftrightarrow ,,,,,,frac{{255}}{x} = frac{{11}}{3} — frac{5}{6},,,,,, Leftrightarrow ,,,,,,,frac{{255}}{x},, = frac{{17}}{6},,,,,,, Leftrightarrow ,,,,,,,x = frac{{255 cdot 6}}{{17}} = 90,) км/ч. Ответ: 90. |