Решение и ответы заданий демонстрационного варианта Проекта ЕГЭ 2023 по математике (профильный уровень). Полное решение. Демоверсия от ФИПИ для 11 класса профиль. Демовариант.
Задание 1.
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
ИЛИ
Площадь треугольника ABC равна 24, DE – средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 2.
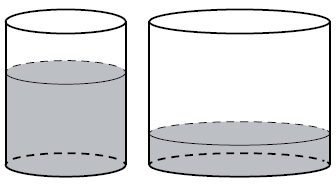
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
ИЛИ
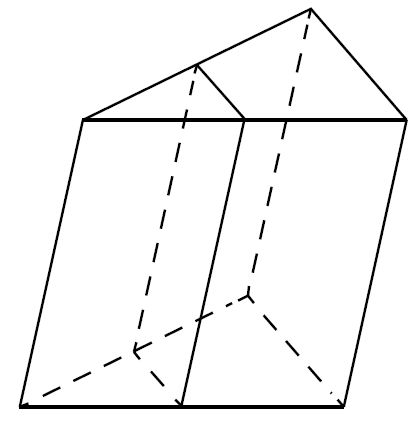
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
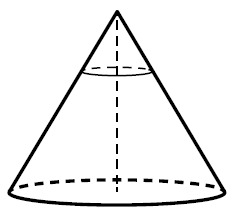
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Задание 3.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Задание 4.
Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
ИЛИ
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Задание 5.
Найдите корень уравнения 3x–5 = 81
ИЛИ
Найдите корень уравнения sqrt{3x+49}=10.
ИЛИ
Найдите корень уравнения log8 (5x + 47) = 3
ИЛИ
Решите уравнение sqrt{2x+3}=x. Если корней окажется несколько, то в ответ запишите наименьший из них.
Задание 6.
Найдите sin2α, ecли cosα = 0,6 и π < α < 2π.
ИЛИ
Найдите значение выражения 16cdot log_{7}sqrt[4]{7}.
ИЛИ
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}.
Задание 7.
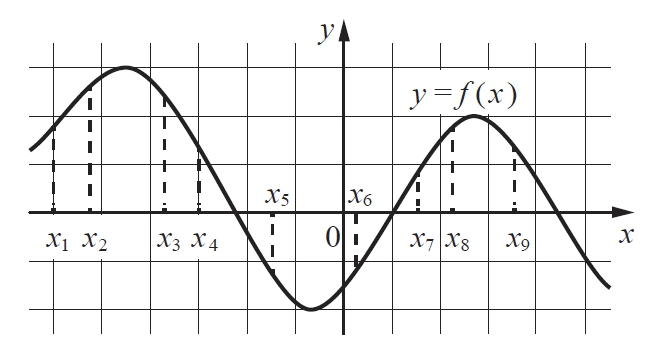
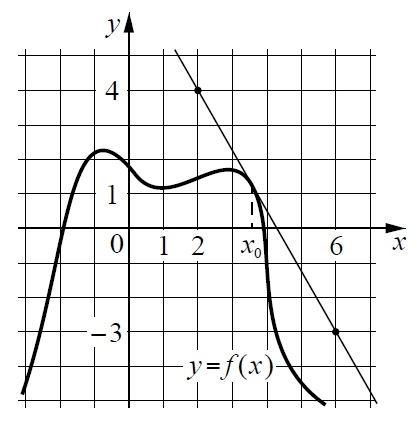
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x1, x2, … x9.
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
ИЛИ
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
Задание 8.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
v=ccdot frac{f–f_{0}}{f+f_{0}},
где с = 1500 м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Задание 9.
Весной катер идёт против течения реки в 1frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Задание 10.
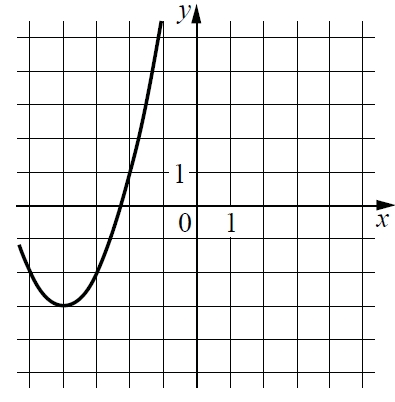
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−12).
Задание 11.
Найдите наименьшее значение функции
y = 9x – 9ln(x + 11) + 7
на отрезке [–10,5 ; 0].
ИЛИ
Найдите точку максимума функции y = (x + 
ИЛИ
Найдите точку минимума функции y=–frac{x}{x^{2}+256}.
Задание 12.
а) Решите уравнение 2sin(x+frac{pi}{2})+cos2x=sqrt{3}cosx+1.
б) Укажите корни этого уравнения, принадлежащие отрезку [-3pi;-frac{3pi}{2}].
Задание 13.
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N – середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Задание 14.
Решите неравенство log_{11}(8x^{2}+7)-log_{11}(x^{2}+x+1)ge log_{11}(frac{x}{x+5}+7).
Задание 15.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задание 16.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Задание 17.
Найдите все положительные значения a, при каждом из которых система
begin{cases} (|x|-5)^{2}+(y-4)^{2}=9, \ (x+2)^{2}+y^{2}=a^{2} end{cases}
имеет единственное решение.
Задание 18.
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Пробники ЕГЭ ↓
Математика,
Физика,
Информатика,
Химия,
Русский,
Обществознание,
Литература,
История,
Иностранные языки,
География,
Биология
1 ноября 2022
В закладки
Обсудить
Жалоба
Пять пробных вариантов ЕГЭ по профильной математике + видеоразбор + конспект.
Разбор пробного варианта ЕГЭ по профильной математике №1
Файл с вариантом: probnyi-variant-1.pdf
Разбор пробного варианта ЕГЭ по профильной математике №2
Файл с вариантом: probnik-2.pdf
Конспект с разбором: konspekt-variant-2.pdf
Разбор пробного варианта ЕГЭ по профильной математике №3
Файл с вариантом: probnik-3.pdf
Конспект с разбором: konspekt-variant-3.pdf
Разбор пробного варианта ЕГЭ по профильной математике №4
Файл с вариантом: probnik-4.pdf
Конспект с разбором: konspekt-razbora-4.pdf
Разбор пробного варианта ЕГЭ по профильной математике №5
Файл с вариантом: probnik_5.pdf
Конспект с разбором: 5_konspekt-s-razborom.pdf
Автор: Марсель Нуртдинов.
Источник: vk.com/marsel_tutor
24 августа вышла демоверсия ЕГЭ 2023 по профильной математике. Для тех, кто пока не готов вникать в тему основательно, успокоительный спойлер: почти ничего не изменилось, принципиально новых заданий нет. Всё в порядке.
А для тех, кто давно был на низком старте и ждал разбор демо ЕГЭ, математик Эйджей провёл стрим с решением заданий из демоверсии ЕГЭ 2023 по профильной математике. В этой статье собраны резюме по заданиям экзамена, которые составители ЕГЭ представили в демоверсии.
https://youtu.be/RFQwP8DW8sA
Что изменилось в ЕГЭ 2023 по профильной математике
По сути, никаких критически важных изменений в демоверсии ЕГЭ 2023 нет, о чём составители написали прямо: «Изменения в содержании КИМ отсутствуют». Но есть момент: все задания из первой части, кроме 11, изменили свои номера.
Будем искать позитивные моменты: если в 2022 году вы не смогли запомнить номера заданий в тесте — ничего страшного, запомните новые в 2023 году.
Главное, что новых заданий не появилось.
Важный момент в самостоятельной подготовке к ЕГЭ по профильной математике — выбор качественных сборников задач. Делимся лучшими ресурсами для повторения теории и отработки практики.
1, 2 задания
В демоверсии ЕГЭ 2023 по профильной математике всё начинается с простой геометрии и стереометрии. Составители хотят, чтобы геометрические задачи научились решать как можно больше ребят, поэтому поместили эти задания вперёд как одни из самых простых, чтобы поднять решаемость.






3, 4 задания
Задания 3–4 посвящены теории вероятности.
Задание 3 — обычная задача наподобие задачи из ОГЭ, а задание 4 — задача про монеты и проценты из КИМа 2022 года.




5, 6 задания
После вероятностей составители ЕГЭ 2023 по профильной математике решили поставить уравнения и выражения. Уравнения ожидаются не супер лёгкие, но вполне решаемые: будут корни, логарифмы и степени. В выражениях в демоверсии ЕГЭ встретилась тригонометрия и степени.






7 задание
Ура, 7 задание осталось на своём месте: это задание с графиком и производными. Почему-то его не объединили в общий блок с 11 заданием, тоже посвящённым производным.

Далее в разборе демоверсии ЕГЭ 2023 по профильной математике выпускников ждут две задачи.
8 задание
8 задача на подстановку: нужно подставить в формулу известные числа и вычислить какую-либо величину. Ничего сложного, главное внимательность.
9 задание
Ещё одна текстовая задача. Здесь могут встретиться темы «Движение по прямой», «Движение по окружности», «Движение по реке» и «Сплавы, смеси, растворы». Такие задачи считаются не самыми простыми. Вместе с Эйджеем разберём этот номер в Телеграме.



10 задание
10 задание в демо ЕГЭ 2023 — «новое старое задание». Этот тип заданий с графиком впервые появился в 2022 году, и в КИМ 2023 попал без изменений. Возможно, стоит ждать усложнения этого задания.
11 задание
Традиционное задание с производными и точками минимума и максимума, которое почему-то не объединили в блок с другим заданием на производные.
Итак, обобщим всё, что мы узнали про первую часть демоверсии ЕГЭ по математике: в 2023 году в экзамене не появились ни вектора, ни комплексные числа. Можно немного расслабиться! Осталось выучить новую нумерацию, и всё будет хорошо.
Нумерация второй части в демоверсии ЕГЭ 2023 осталась без изменений, и это радует: не придётся переучивать номера и переживать. Посмотрим, что приготовили составители в этом году.
12 задание
Традиционно в разборе демоверсии ЕГЭ 2023 по профильной математике в 12 задании выпускников ждёт тригонометрическое уравнение.
13 задание
В 13 задании осталась стереометрия: в демоверсии представлена треугольная призма.
14 задание
В 14 задании всё по плану, там остались неравенства с логарифмами, ничего нового.
Это задание вместе с 12-ым составляет «джентльменский набор» из второй части — их под силу решить каждому, и этому нужно обязательно научиться, чтобы набрать 70+ баллов за ЕГЭ по профильной математике.
15 задание
15 задание также считается вполне решаемым. В демоверсии это экономическая задача про человека, который взял кредит в банке и рассчитывает выплаты и проценты.
16 задание
В задании 16 демоверсии ЕГЭ 2023 представлена планиметрическая задача про две окружности.
17 задание
Задача на параметр. Как показывает практика прошлых лет, параметр — самое решаемое задание из сложных заданий ЕГЭ.

18 задание
Задача на целые числа. Из трёх пунктов, А и Б решить может каждый, если хорошо подготовиться.
Чтобы получить 80+ баллов по профильной математике, нужно без ошибок решить первую часть и выполнить 12, 14, 15 и 18аб задания. А планиметрия, стереометрия, параметр и 18 задание полностью помогут получить заветную сотку. Как повысить свои шансы на успешную сдачу ЕГЭ по математике, рассказали в нашей статье.
Мы разобрали демоверсию ЕГЭ 2023 по математике, и теперь вы знаете, что приготовили для вас составители экзамена. Можно смело начинать подготовку! Эйджей уже составил план занятий и ждёт вас на курсе «Основа». Это возможность разобраться во всех темах и набить руку в решении заданий в компании единомышленников и с личным наставником.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Задание 1
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Скрыть
Задание 2
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Скрыть
Задание 3
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Скрыть
Задание 4
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Ответ: 0,89
Скрыть
Задание 5
Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$
Ответ: -0,2
Скрыть
Задание 6
Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$
Ответ: 0,5
Скрыть
Задание 7
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.
Ответ: 5
Скрыть
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.
Ответ: 5,832
Скрыть
Задание 9
Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Скрыть
Задание 10
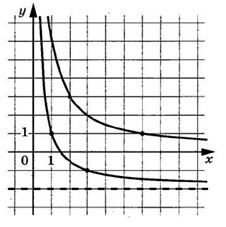
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$
Ответ: -2910
Скрыть
Задание 12
а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$
Скрыть
Задание 13
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.
б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.
Ответ: 24
Скрыть
Задание 14
Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$
Ответ: $$(-infty;1];[log_{4} 28;2,5)$$
Скрыть
Задание 15
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— платежи в 2028 и 2029 годах должны быть равными;
— к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
Ответ: 400 тыс. руб.
Скрыть
Задание 16
В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.
а) Докажите, что $$AL:AC=AB:BC$$.
б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.
Ответ: 14,2
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.
Ответ: (-4;-3);(-3;-1);(-1;0)
Скрыть
Задание 18
Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Ответ: а)да б)нет в)195
Скрыть