Решение заданий по алгебре по егэ

В данном разделе мы занимаемся подготовкой к ЕГЭ по математике как базового, профильного уровня — у нас представлены разборы задач, тесты, описание экзамена и полезные рекомендации. Пользуясь нашим ресурсом, вы как минимум разберетесь в решении задач и сможете успешно сдать ЕГЭ по математике в 2020 году. Начинаем!

ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида — базовый и профильный. В данном разделе я приведен разбор каждого вида заданий с подробным объяснением для двух вариантов. Задания ЕГЭ строго тематические, поэтому для каждого номера можно дать точные рекомендации и привести теорию, необходимую именно для решения данного вида задания. Ниже вы найдете ссылки на задания, перейдя по которым можно изучить теорию и разобрать примеры. Примеры постоянно пополняются и актуализируются.

---

Структура базового уровня ЕГЭ по математике

---

Экзаменационная работа по математике базового уровня состоит из одной части, включающей 20 заданий с кратким ответом. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Ответом к каждому из заданий 1–20 является целое число, конечная десятичная дробь, или последовательность цифр.

Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.

---

Разбор заданий ЕГЭ по математике (база)

---

Сдай ЕГЭ! Бесплатные материалы для
подготовки каждую неделю!

null

Нажимая на кнопку, вы даете согласие на обработку своих персональных
данных согласно 152-ФЗ. Подробнее

Материалы для подготовки к ЕГЭ по математике базового и профильного уровня

Полный спектр материалов для подготовки к ЕГЭ по математике + решение задач по всем темам ЕГЭ. В каждой теме и каждой задаче есть свои секреты. О них вам может рассказать только очень хороший учитель или репетитор. Такой, как мы. Читайте, изучайте, скачивайте то, чего не найдёте в учебниках! Вы можете скачать весь курс бесплатно сразу или найти то, что ищете, на этой странице.

Справочник для подготовки к ЕГЭ Анны Малковой
Актуальные видео по математике

к оглавлению ▴

Полный курс для подготовки к ЕГЭ по математике

• ^New

  ЕГЭ-2022, математика. Все задачи с решениями

• ^New

  Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения

• ^New

  Тренировочная работа от 28.09.2021, Статград. Задача №18 (Числа и их свойства)

• ^New

  Новые задачи по теории вероятностей из Открытого Банка заданий ЕГЭ, 2021-2022 год

• ^New

  Комплексные числа на ЕГЭ по математике

• ^New

  ЕГЭ-2021, Математика. Все задачи

• ^New

  Тренировочная работа № 3. Задачи 13-19

• ^New

  Задача с секретом о пиратах и дукатах из сборника И. В. Ященко

• Стрим 20 августа 2020 года. Лучшие задачи ЕГЭ-2020

• ЕГЭ-2020 по математике. Сложные задачи, неравноценные варианты и одно неравенство для всей страны

• Тренировочная работа 18 декабря 2019 года. Задача 19
• Учителю и репетитору: Методика, программы подготовки к ЕГЭ, поурочные планы
• Тесты и варианты ЕГЭ с решениями и ответами
• Алгебра – основные понятия и формулы
• Теория вероятностей
• Текстовые задачи
• Решение уравнений
• Решение неравенств
• Тригонометрия
• Планиметрия
• Стереометрия
• Функции и графики. Производная и первообразная
• «Экономические» задачи на ЕГЭ по математике
• Задачи с параметрами
• Нестандартные задачи на числа и их свойства
• Советы и рекомендации для подготовки к ЕГЭ по математике

к оглавлению ▴

Профильный ЕГЭ по математике. Все задачи

• Задание 1. Планиметрия
• Задание 2. Стереометрия
• Задание 3. Теория вероятностей. Основные понятия
• Задание 4. Теория вероятностей, повышенный уровень сложности
• Задание 5. Простейшие уравнения
• Задание 6. Вычисления и преобразования
• Задание 7. Производная и первообразная
• Задание 8. Задачи с прикладным содержанием
• Задание 9. Текстовые задачи
• Задание 10. Функции и графики
• Задание 11. Исследование функций
• Задание 12. Уравнения на ЕГЭ по математике
• Задание 13. Стереометрия на ЕГЭ по математике
• Задание 14. Неравенства на ЕГЭ по математике
• Задание 15. «Экономические» задачи на ЕГЭ по математике
• Задание 16. Планиметрия на ЕГЭ по математике
• Задание 17. Задачи с параметрами на ЕГЭ по математике
• Задание 18. Задачи на числа и их свойства на ЕГЭ по математике Нестандартные задачи
• Таблица перевода баллов ЕГЭ, Профильный уровень

Как решалась задача №17 на ЕГЭ-2018?

к оглавлению ▴

Варианты Статград

^New

Тренировочная работа № 3. Задачи 13-19

Тренировочная работа 29.01.20. Вариант Восток

Тренировочная работа 29.01.20. Вариант Запад

Тренировочная работа 25.09.19. Вариант Запад

Тренировочная работа 25.09.19. Вариант Восток

Тренировочная работа 24.01.19. Вариант Запад

Тренировочная работа 24.01.19. Вариант Восток

Тренировочная работа 18.12.19 Вариант Запад

Тренировочная работа 30.09.20

Диагностическая работа 16.12.20

Досрочный ЕГЭ 2020 года, Профильная математика

Новая задача 18 Профильного ЕГЭ по математике (числа и их свойства), январь, восток

Новая задача 18 Профильного ЕГЭ по математике, Параметры, 24 января 2019, запад

Новая задача 16 Профильного ЕГЭ по математике, Геометрия, январь, запад

к оглавлению ▴

Задачи из сборника И. В. Ященко, 2021 год

• Вариант 1, Задача 13
• Вариант 6, Задача 13
• Вариант 11, Задача 13
• Вариант 17, Задача 13
• Вариант 22, Задача 13
• Вариант 28, Задача 13
• Вариант 1, Задача 15
• Вариант 3, Задача 15
• Вариант 5, Задача 15
• Вариант 12, Задача 15
• Вариант 17, Задача 15
• Вариант 24, Задача 15
• Задача 18. Пираты и дукаты

к оглавлению ▴

Задачи из сборника И. В. Ященко, 2020 год

• Вариант 6, задача 14
• Вариант 8, задача 15
• Вариант 32, задача 15
• Вариант 36, задача 15
• Вариант 2, задача 16
• Вариант 4, задача 16
• Вариант 6, задача 16
• Вариант 8, задача 16
• Вариант 12, задача 16
• Вариант 1, задача 17
• Вариант 5, задача 17
• Вариант 11, задача 17
• Вариант 26, задача 17
• Вариант 36, задача 17
• Вариант 27, задача 19

к оглавлению ▴

Новые варианты для подготовки к ЕГЭ и ОГЭ с ответами и решениями:

к оглавлению ▴

Выберите раздел:

к оглавлению ▴

Необходимый минимум

• • Задача 1. Решается всегда!
  • Задача 2. Чтение графика функции

• Теория вероятностей. Основные понятия.

• ^{Видео бесплатно!}

  Теория вероятностей на ЕГЭ по математике. Полный курс.

• Текстовые задачи. Движение и работа
• Текстовые задачи. Проценты, сплавы, растворы…
• ЕГЭ без ошибок. Вычисляем без калькулятора

к оглавлению ▴

Планиметрия

• Геометрия. Формулы площадей фигур.
• Программа по геометрии. Список необходимых фактов и теорем.
• Синус, косинус и тангенс острого угла прямоугольного треугольника
• Тригонометрический круг: вся тригонометрия на одном рисунке
• Внешний угол треугольника. Синус и косинус внешнего угла
• Высота в прямоугольном треугольнике
• Сумма углов треугольника
• Углы при параллельных прямых и секущей
• Высоты, медианы, биссектрисы треугольника
• Четырёхугольники
• Параллелограмм
• Прямоугольник
• Ромб
• Квадрат
• Трапеция
• Окружность. Центральный и вписанный угол
• Касательная к окружности
• Вписанные и описанные треугольники. Теорема синусов
• Вписанные и описанные четырёхугольники
• Правильный треугольник
• Правильный шестиугольник
• Векторы и операции над ними
• Геометрия в школе: засада для абитуриента
• Геометрический парадокс: Прямой угол равен тупому
• Геометрический парадокс: Катет равен гипотенузе

к оглавлению ▴

Алгебра

• Числовые множества
• Степени и корни.
• Что такое функция?
• Чтение графика функции
• Парабола и квадратные неравенства.
• Степенная функция
• Показательная функция
• Показательные уравнения
• Логарифмы
• Логарифмическая функция
• Элементарные функции и их графики
• Показательные и логарифмические неравенства. 1
• Показательные и логарифмические неравенства. 2
• Число e

• ^{Видео бесплатно!}

  Производная функции. Геометрический смысл производной

• Таблица производных и правила дифференцирования
• Модуль числа
• Уравнения и неравенства с модулем
• Метод интервалов

к оглавлению ▴

Тригонометрия

• Тригонометрический круг: вся тригонометрия на одном рисунке
• Тригонометрические формулы. Необходимый минимум

• ^{Видео бесплатно!}

  Формулы приведения

• Тригонометрические формулы. Сводка для части 1
• Тригонометрические формулы. Сводка для части 2
• Тригонометрические функции
• Простейшие тригонометрические уравнения, 1
• Простейшие тригонометрические уравнения, 2
• Тригонометрические уравнения

к оглавлению ▴

Стереометрия

• Многогранники: формулы объема и площади поверхности
• Тела вращения: формулы объема и площади поверхности
• Задачи по стереометрии часть 1: Просто применяем формулы
• Задачи по стереометрии часть 2: Приемы и секреты
• Задача 14 (часть 2 ЕГЭ по математике). Программа по стереометрии
• Плоскость в пространстве. Взаимное расположение плоскостей
• Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые
• Параллельность прямой и плоскости
• Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости
• Параллельность плоскостей
• Угол между плоскостями. Перпендикулярность плоскостей
• Угол и расстояние между скрещивающимися прямыми. Расстояние от точки до плоскости
• Теорема о трёх перпендикулярах
• Параллельное проецирование
• Как строить чертежи в задачах по стереометрии
• Векторы и метод координат в задаче 14, часть 2 ЕГЭ по математике
• В.М. Мамаева. «Перпендикулярность. Книга для учащихся»
• В.М. Мамаева. «Перпендикулярность. Книга для учителя»
• В.М. Мамаева. «Тела вращения. Книга для учащихся»
• В.М. Мамаева. «Тела вращения. Книга для учителя»

к оглавлению ▴

Часть 2 (задачи 13 — 19) на ЕГЭ по математике.

^Видео

Задача 13: Уравнения на ЕГЭ по математике. Полный курс.

^Видео

Задача 14: Стереометрия на ЕГЭ по математике. Полный курс. Оба метода — классика и векторы. Более 3 часов видео.

^Видео

Задача 15: Неравенства на ЕГЭ по математике. Полный курс в двух частях.

^Видео

Задача 16: Геометрия на ЕГЭ по математике. Полный курс. Более 5 часов видео.

^Видео

Задачи по математике с экономическим содержанием. Задача 17 на ЕГЭ по математике и задачи олимпиад по экономике.

^{Видео бесплатно!}

Задача 18: Параметры на ЕГЭ по математике. Графический метод.

^Видео

Задача 18: Параметры на ЕГЭ по математике. Полный курс. Более 5 часов видео.
Задача 19 на числа и их свойства на ЕГЭ по математике.

Задача 19 на ЕГЭ по математике 2016 года. Решение.
Задача 19 на ЕГЭ по математике 2017 года. Решение.

^Видео

Впервые! Видеокурс «Ключ к С6». Нестандартные задачи на ЕГЭ по математике.

к оглавлению ▴

Советы и рекомендации по подготовке к экзамену

• Справочники для подготовки к ЕГЭ по математике
• Методика подготовки к ЕГЭ по математике Анны Малковой
• ЕГЭ по математике – советы и рекомендации
• Репетитор по математике
• Подготовиться к ЕГЭ самостоятельно и бесплатно
• Математика и жизнь. Из воспоминаний бывалого студента.
• Книги и учебники для подготовки к ЕГЭ по Математике
• Как подготовиться к ЕГЭ по математике?
• Как распределить время на ЕГЭ по математике
• Подготовка к ЕГЭ по Математике с нуля
• Самостоятельная подготовка к ЕГЭ по математике

к оглавлению ▴

Об этом сайте:

• Каждый год на этом сайте готовятся к ЕГЭ сотни тысяч учащихся. Нас рекомендуют учителя и репетиторы. Автор сайта, на котором вы находитесь, — репетитор-профессионал, ведущая курсов подготовки к ЕГЭ на высшие баллы, руководитель компании «ЕГЭ-Студия» Анна Георгиевна Малкова.
  Также вы можете выбрать базовый уровень подготовки к ЕГЭ по математике онлайн

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут). 

Минимальный порог — 27 баллов.

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий. 

Определяющим признаком каждой части работы является форма заданий:

• часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
• часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).

---

Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:  

«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».

---

Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.

Пример 1.

В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м  холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.

Решение:

1)    Найдем количество потраченной воды за месяц:

177 — 172 = 5 (куб м)

2)    Найдем сколько денег заплатят за потраченную воду:

34,17 · 5 = 170,85 (руб)

Ответ: 170,85.

---

---

Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами  и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.

#ADVERTISING_INSERT#

Задание №  2 проверяет умение читать диаграммы.

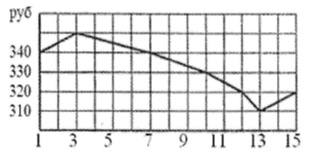
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?

Решение: 

1)    340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.

2)    1000 · 3/4 = 750 (акций) — составляют  3/4 от всех купленных акций.

3)    330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.

4)    1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.

5)    310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.

6)    247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.

7)    340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.

Ответ: 15000.

---

Задание № 3 — является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.

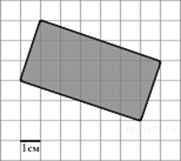
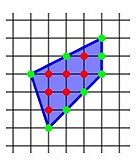
Пример 3. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение: Для вычисления площади данной фигуры можно воспользоваться формулой Пика:

На рисунке справа B = 7 (красные точки), Г = 8 (зелёные точки),  Для вычисления площади данного прямоугольника воспользуемся формулой Пика:  где В = 10, Г = 6, поэтому Ответ: 20.

---

Читайте также: ЕГЭ по физике: решение задач о колебаниях

---

Задание № 4 — задача курса «Теория вероятностей и статистика». Проверяется умение вычислять вероятность события в простейшей ситуации.

Пример 4. На окружности отмечены 5 красных и 1 синяя точка. Определите, каких многоугольников больше: тех, у которых все вершины красные, или тех, у которых одна из вершин синяя. В ответе укажите, на сколько одних больше, чем других.

Решение: 1) Воспользуемся формулой числа сочетаний из n элементов по k:

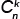=	n!	.
k!(n – k)!

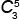=	5!	=	3! · 4 · 5	=	4 · 5	= 10 треугольников,
3!(5 – 3)!	3!2!	1 · 2

у которых все вершины красные.

2)

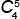=	5!	=	4! · 5	= 5 треугольников,
4!(5 – 4)!	4!1!

у которых все вершины красные.

3) Один пятиугольник, у которого все вершины красные.

4) 10 + 5 + 1 = 16 многоугольников, у которых все вершины красные.

5)

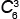=	6!	=	3! · 4 · 5 · 6	=	4 · 5 · 6	= 20 треугольников,
3!(6 – 3)!	3!3!	1 · 2 · 3

у которых вершины красные или с одной синей вершиной.

6)

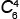=	6!	=	4! · 5 · 6	=	5 · 6	= 15 четырёхуголников,
4!(6 – 4)!	4!2!	1 · 2

у которых вершины красные или с одной синей вершиной.

7)

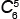=	6!	=	5! · 6	= 6 пятиугольников,
5!(6 – 5)!	5!1!

у которых вершины красные или с одной синей вершиной.

Один шестиуголник, у которого вершины красные с одной синей вершиной.

9) 20 + 15 + 6 + 1 = 42 многоуголника, у которых все вершины красные или с одной синей вершиной.

10) 42 – 16 = 26 многоугольников, в которых используется синяя точка.

11) 26 – 16 = 10 многоугольников – на сколько многоугольников, у которых одна из вершин — синяя точка, больше, чем многоугольников, у которых все вершины только красные.

Ответ: 10.

---

Задание № 5 — базового уровня первой части проверяет умения решать простейшие уравнения (иррациональные, показательные, тригонометрические, логарифмические).

Пример 5. Решите уравнение 2^3 + x = 0,4 · 5^3 + x.

Решение. Разделим обе части данного уравнения на 5^3 + х ≠ 0, получим

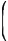
23 + x	= 0,4 или		2		3 + х	=	2	,
53 + х	5		5

откуда следует, что 3 + x = 1, x = –2.

Ответ: –2.

---

Задание № 6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.

Пример 6. Площадь треугольника ABC равна 129. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

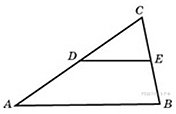
Решение. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол СDE равен углу CAB как соответственные углы при DE || AB секущей AC. Так как DE – средняя линия треугольника по условию, то по свойству средней линии | DE = (1/2)AB. Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому

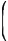
SΔCDE	=		2		2	; SΔCDE  =	1	· 129 = 32,25.
SΔCAB	5		4

Следовательно, S_ABED = S_ΔABC – S_ΔCDE = 129 – 32,25 = 96,75. 

Ответ: 96,75.

---

Смотреть вебинары по алгебре

---

Задание № 7 — проверяет применение производной к исследованию функции. Для успешного выполнения необходимо содержательное, не формальное владение понятием производной.

Пример 7. К графику функции y = f(x) в точке с абсциссой x₀ проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; –1) этого графика. Найдите f′(x₀).

Решение. 1) Воспользуемся уравнением прямой, проходящей через две заданные точки и найдём уравнение прямой, проходящей через точки (4; 3) и (3; –1).

(y – y₁)(x₂ – x₁) = (x – x₁)(y₂ – y₁)

(y – 3)(3 – 4) = (x – 4)(–1 – 3)

(y – 3)(–1) = (x – 4)(–4)

–y + 3 = –4x + 16| · (–1)

y – 3 = 4x – 16

y = 4x – 13, где k₁ = 4.

2) Найдём угловой коэффициент касательной k₂, которая перпендикулярна прямой y = 4x – 13, где k₁ = 4, по формуле:

k1 · k2 = –1, k2 =	–1	–0,25.
4

3) Угловой коэффициент касательной – производная функции в точке касания. Значит, f′(x₀) = k₂ = –0,25.

Ответ: –0,25.

---

Задание № 8 — проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов   фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.

Пример 8. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

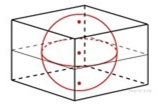
Решение. 1) V_куба = a³ (где а – длина ребра куба), поэтому

а³ = 216

а = ³√216

a = 6.

2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = a, d = 6, d = 2R, R = 6 : 2 = 3.

Ответ: 3.

---

Приемы подготовки к профильному ЕГЭ по математике

---

Задание № 9 — требует от выпускника навыков преобразования и упрощения алгебраических выражений. Задание № 9 повышенного уровня сложности с кратким ответом. Задания из раздела «Вычисления и преобразования» в ЕГЭ подразделяются на несколько видов:

1. преобразования числовых рациональных выражений;

2. преобразования алгебраических выражений и дробей;

3. преобразования числовых/буквенных иррациональных выражений;

4. действия со степенями;

5. преобразование логарифмических выражений;

6. преобразования числовых/буквенных тригонометрических выражений.

Пример 9. Вычислите tgα, если известно, что cos2α  = 0,6 и

Решение. 1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos²α – 1 и найдём

cos2α =	cos2α + 1	=	0,6 + 1	=	1,6	= 0,8.
2	2	2

2) Воспользуемся формулой тригонометрических функций одного угла:

и найдём

tg2α =	1	– 1 =	1	– 1 =	10	– 1 =	5	– 1 = 1	1	– 1 =	1	= 0,25.
cos2α	0,8	8	4	4	4

Значит, tg²α = ± 0,5.

3) По условию

значит, α – угол II четверти и tgα < 0, поэтому tgα = –0,5.

Ответ: –0,5.

---

#ADVERTISING_INSERT#

---

Задание № 10 — проверяет у учащихся умение использовать приобретенные раннее знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен получиться в виде целого числа или конечной десятичной дроби.

Пример 10. Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q = mv²sin²α. Под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение. Для решения задачи нам необходимо решить неравенство Q ≥ 50,  на  интервале 2α ∈ (0°; 180°). 

mv²sin²α ≥ 50

2· 10²sin²α ≥ 50

200 · sin²α ≥ 50

Решением данного неравенства являются два неравенства:

sinα ≥	1	и sinα ≤ –	1	.
2	2

Так как α ∈ (0°; 90°), то будем решать только

 Неравенство

 мы не рассматриваем, так как α для него будет более 180°. Итак:

Изобразим решение неравенства графически:

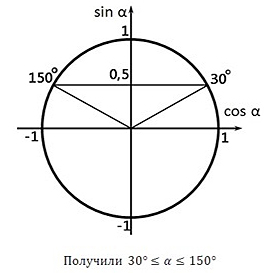
Так как по условию α ∈ (0°; 90°), значит 30° ≤ α < 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.

Ответ: 60.

---

Скачать бесплатно рабочие программы по алгебре

---

Задание № 11 — является типовым, но оказывается непростым для учащихся. Главным источником затруднений является построение математической модели (составление уравнения). Задание № 11 проверяет умение решать текстовые задачи.

Пример 11. На весенних каникулах 11-классник Вася должен был решить 560 тренировочных задач для подготовки к ЕГЭ. 18 марта в последний учебный день Вася решил 5 задач. Далее ежедневно он решал на одно и то же количество задач больше по сравнению с предыдущим днём. Определите, сколько задач Вася решил 2 апреля в последний день каникул.

Решение:

Обозначим a₁ = 5 – количество задач, которые Вася решил 18 марта, d – ежедневное количество задач, решаемых Васей, n = 16 – количество дней с 18 марта по 2 апреля включительно, S₁₆ = 560 – общее количество задач, a₁₆ – количество задач, которые Вася решил 2 апреля. Зная, что ежедневно Вася решал на одно и то же количество задач больше по сравнению с предыдущим днём, то можно использовать формулы нахождения суммы арифметической прогрессии:

560 = (5 + a₁₆) · 8,

5 + a₁₆ = 560 : 8,

5 + a₁₆ = 70,

a₁₆ = 70 – 5

a₁₆ = 65.

Значит, Вася решил 2 апреля 65 задач.

Ответ: 65.

---

Задание № 12 — проверяют у учащихся умение выполнять действия с функциями, уметь применять производную к исследованию функции.

Пример 12. Найти точку максимума функции y = 10ln(x + 9) – 10x + 1.

Решение: 1) Найдем область определения функции: x + 9 > 0, x > –9,  то есть x ∈ (–9; ∞).

2) Найдем производную функции:

3) Найдем нули производной:

y′= 0,	10	– 10 = 0, x = –8.
x + 9

4) Найденная точка принадлежит промежутку (–9; ∞). Определим знаки производной функции и изобразим на рисунке поведение функции:

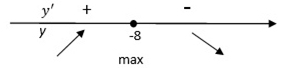
Искомая точка максимума  x = –8.

Ответ: –8.

---

Скачать бесплатно рабочую программу по математике к УМК Мерзляка А.Г. 5-11 класс

Скачать бесплатно рабочую программу по математике к линии УМК Г.К. Муравина, К.С. Муравина, О.В. Муравиной 10-11

---

---

Скачать бесплатно методические пособия по алгебре

---

 
Задание № 13 — повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.

Пример 13. а) Решите уравнение  2log₃²(2cosx) – 5log₃(2cosx) + 2 = 0

б) Найдите все корни этого уравнения, принадлежащие отрезку .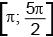

Решение: а) Пусть log₃(2cosx) = t, тогда 2t² – 5t + 2 = 0,

откуда  t = 2 или t =	1	.
2

	log3(2cosx)  =	2	⇔		2cosx = 9	⇔		cosx =	4,5	⇔  т.к.  |cosx| ≤ 1,
log3(2cosx)  =	1	2cosx = √3	cosx =	√3
2	2

	x  =	π	+ 2πk
6
x  = –	π	+ 2πk, k ∈ Z
6

б) Найдём корни, лежащие на отрезке .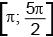

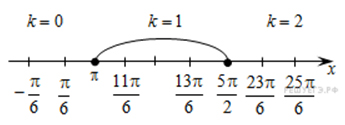
Из рисунка видно, что заданному отрезку принадлежат корни

Ответ: а)	π	+ 2πk; –	π	+ 2πk, k ∈ Z; б)	11π	;	13π	.
6	6	6	6

---

Задание № 14 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить. 

Пример 14. Диаметр окружности основания цилиндра равен  20, образующая цилиндра равна  28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.

а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

Решение: а)  Хорда длиной 12 находится на расстоянии 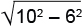 = 8  от центра окружности основания, а хорда длиной 16, аналогично, – на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14,  либо 8 − 6 = 2. 

Тогда расстояние между хордами составляет либо

 =  = √980 =  = 2√245 

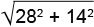
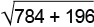
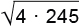
либо

 =  = √788 =  = 2√197.

По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.

б) Обозначим центры оснований  за О₁ и О₂. Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей  A и проекцию  A на второе основание — H (H ∈ β). Тогда  AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.

Значит, искомый угол равен

∠ABH = arctg	AH	= arctg	28	= arctg14.
BH	8 – 6

Ответ: arctg 14.

---

Подготовка к ОГЭ и ЕГЭ для учителей по алгебре

---

Задание № 15 — повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.

Пример 15. Решите неравенство |x² – 3x| · log₂(x + 1) ≤ 3x – x².

Решение: Областью определения данного неравенства является интервал (–1; +∞). Рассмотри отдельно три случая:

1) Пусть x² – 3x = 0, т.е. х = 0 или х = 3. В этом случае данное неравенство превращается в верное, следовательно, эти значения входят в решение.

2) Пусть теперь x² – 3x > 0, т.е. x ∈ (–1; 0) ∪ (3; +∞). При этом данное неравенство можно переписать в виде (x² – 3x) · log₂(x + 1) ≤ 3x – x² и разделить на положительное выражение x² – 3x. Получим log₂(x + 1) ≤ –1, x + 1 ≤ 2^–1, x ≤ 0,5 –1 или x ≤ –0,5. Учитывая область определения, имеем x ∈ (–1; –0,5].

3) Наконец, рассмотрим x² – 3x < 0, при этом x ∈ (0; 3). При этом исходное неравенство перепишется в виде (3x – x²) · log₂(x + 1) ≤ 3x – x². После деления на положительное выражение 3x – x², получим log₂(x + 1) ≤ 1, x + 1 ≤ 2, x ≤ 1. Учитывая область, имеем x ∈ (0; 1].

Объединяя полученные решения, получаем x ∈ (–1; –0.5] ∪ [0; 1] ∪ {3}.

Ответ: (–1; –0.5] ∪ [0; 1] ∪ {3}.

---

Задание № 16 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить. 

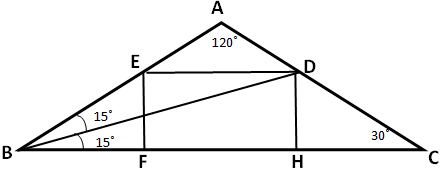
Пример 16. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.

Решение: а)

1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = 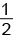 BE по свойству катета, лежащего против угла 30°.

2) Пусть EF = DH = x, тогда BE = 2x, BF = x√3 по теореме Пифагора.

3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.

BD – биссектриса ∠B, значит   ∠ABD  =  ∠DBC = 15˚.

4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.

tg 15° = tg(45° – 30°) =	3 – √3	,
3 + √3

3 – √3	,	x
3 + √3	x√3 + FH

(x√3 + FH)(3 – √3) = x(3 + √3)

2√3x – 6x = √3FH – 3FH

2x(√3 – 3) = FH(√3 – 3)

FH = 2x

FH = 2DH

Что требовалось доказать.

б) 1) ΔAED ∼ ΔABC по двум углам, так как ∠B – общий, ∠AED = ∠ABC как соответственные при ED || BC секущей AB. Из подобия треугольников следует:

 √3 – 1 = 2 – x

x = 3 – √3

EF = 3 – √3

2) S_DEFH = ED · EF = (3 – √3) · 2(3 – √3)

S_DEFH = 24 – 12√3.

Ответ: 24 – 12√3.

---

Задание № 17 — задание с развернутым ответом, это задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Это задание — текстовая задача с экономическим содержанием.

Пример 17. Вклад в размере 20 млн  рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10%  по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн. рублей, где х — целое число. Найдите наибольшее значение  х, при котором банк за четыре года начислит на вклад меньше 17 млн рублей.

Решение: В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн рублей, а в конце второго – 22 + 22 · 0,1 = 24,2 млн рублей. В начале третьего года вклад (в млн рублей) составит  (24,2 + х), а в конце — (24,2 + х) + (24,2 + х) · 0,1 = (26,62 + 1,1х). В начале четвёртого года вклад составит (26,62 + 2,1х),  а в конце — (26,62 + 2,1х) + (26,62 + 2,1х) · 0,1 = (29,282 + 2,31х). По условию, нужно найти наибольшее целое х, для которого выполнено неравенство 

(29,282 + 2,31x) – 20 – 2x < 17

29,282 + 2,31x – 20 – 2x < 17

0,31x < 17 + 20 – 29,282

0,31x < 7,718

Наибольшее целое решение этого неравенства — число 24. 

Ответ: 24.

---

Задание № 18 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 18 необходим, кроме прочных математических знаний, также высокий уровень математической культуры.

Пример 18. При каких a система неравенств

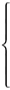	x2 + y2 ≤ 2ay – a2 + 1
y + a ≤ |x| – a

имеет ровно два решения?

Решение: Данную систему можно переписать в виде

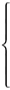	x2 + (y – a)2 ≤ 1
y ≤ |x| – a

Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y = |x| – a,причём последний есть график функции
y = |x|, сдвинутый вниз на а. Решение данной системы есть пересечение множеств решений каждого из неравенств.

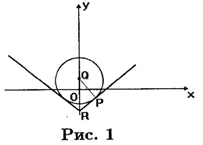
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.

Точки касания круга с прямыми и будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит, треугольник PQR – прямоугольный равнобедренный. Точка Q имеет координаты (0, а), а точка R – координаты (0, –а). Кроме того, отрезки PR и PQ равны радиусу окружности, равному 1. Значит,

---

Перейти в каталог продукции по алгебре

---

Задание № 19 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 19 необходимо уметь осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы.

Пример 19. Пусть Sn сумма п членов арифметической прогрессии (а_п). Известно, что S_{n + 1} = 2n² – 21n – 23.

а) Укажите формулу п-го члена этой прогрессии.

б) Найдите наименьшую по модулю сумму S_n.

в) Найдите наименьшее п, при котором S_n будет квадратом целого числа.

Решение: а) Очевидно, что a_n = S_n – S_{n – 1}. Используя данную формулу, получаем:

S_n = S_{(n – 1) + 1} = 2(n – 1)² – 21(n – 1) – 23 = 2n² – 25n,

S_{n – 1} = S_{(n – 2) + 1} = 2(n – 1)² – 21(n – 2) – 23 = 2n² – 25n + 27

значит, a_n = 2n² – 25n – (2n² – 29n + 27) = 4n – 27.

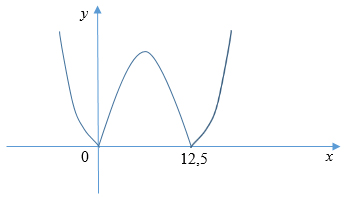
б) Так как S_n = 2n² – 25n, то рассмотрим функцию S(x) = |2x² – 25x|. Ее график можно увидеть на рисунке.

Очевидно, что наименьшее значение достигается в целочисленных точках, расположенных наиболее близко к нулям функции. Очевидно, что это точки х = 1, х = 12 и х = 13. Поскольку, S(1) = |S₁| = |2 – 25| = 23, S(12) = |S₁₂| = |2 · 144 – 25 · 12| = 12, S(13) = |S₁₃| = |2 · 169 – 25 · 13| = 13, то наименьшее значение равно 12.

в) Из предыдущего пункта вытекает, что Sn положительно, начиная с n = 13. Так как S_n = 2n² – 25n = n(2n – 25), то очевидный случай, когда данное выражение является полным квадратом, реализуется при n = 2n – 25, то есть при п = 25.

Осталось проверить значения с 13 до 25:

S₁₃ = 13 · 1, S₁₄ = 14 · 3, S₁₅ = 15 · 5, S₁₆ = 16 · 7, S₁₇ = 17 · 9, S₁₈ = 18 · 11, S₁₉ = 19 · 13, S₂₀ = 20 · 13, S₂₁ = 21 · 17, S₂₂ = 22 · 19, S₂₃ = 23 · 21, S₂₄ = 24 · 23.

Получается, что при меньших значениях п полный квадрат не достигается.

Ответ: а) a_n = 4n – 27; б) 12; в) 25.

Фото: nn.ucheba.ru

________________

*С мая 2017 года объединенная издательская группа «ДРОФА-ВЕНТАНА» входит в корпорацию «Российский учебник». В корпорацию также вошли издательство «Астрель» и цифровая образовательная платформа «LECTA». Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства «ДРОФА» в сфере цифрового образования (электронные формы учебников, «Российская электронная школа», цифровая образовательная платформа LECTA). До прихода в издательство «ДРОФА» занимал позицию вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». Сегодня издательская корпорация «Российский учебник» обладает самым крупным портфелем учебников, включенных в Федеральный перечень — 485 наименований (примерно 40%, без учета учебников для коррекционной школы). Издательствам корпорации принадлежат наиболее востребованные российскими школами комплекты учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые нужны для развития производственного потенциала страны. В портфель корпорации входят учебники и учебные пособия для начальной школы, удостоенные Премии Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.

© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.

Задания ЕГЭ по математике

• 
  21.02.2019

  Задачи о кредитном контракте ЕГЭ по математике

  
  (14032)
  

• 
  10.10.2018

  Решение задания 1 ЕГЭ 2021 по математике

  
  (55532)
  

• 
  10.10.2018

  Решение задания 2 ЕГЭ 2021 по математике

  
  (17527)
  

• 
  10.10.2018

  Решение задания 3 ЕГЭ 2021 по математике

  
  (37054)
  

• 
  10.10.2018

  Решение задания 4 ЕГЭ 2021 по математике

  
  (35535)
  

• 
  10.10.2018

  Решение задания 5 ЕГЭ 2021 по математике

  
  (27963)
  

• 
  10.10.2018

  Решение задания 6 ЕГЭ 2021 по математике

  
  (35957)
  

• 
  10.10.2018

  Решение задания 7 ЕГЭ 2021 по математике

  
  (35885)
  

• 
  10.10.2018

  Решение задания 8 ЕГЭ 2021 по математике

  
  (29352)
  

• 
  10.10.2018

  Решение задания 9 ЕГЭ 2021 по математике

  
  (32088)
  

• 
  10.10.2018

  Решение задания 10 ЕГЭ 2021 по математике

  
  (24669)
  

• 
  10.10.2018

  Решение задания 11 ЕГЭ 2021 по математике

  
  (29330)
  

• 
  10.10.2018

  Решение задания 12 ЕГЭ по математике

  
  (29860)
  

• 
  10.10.2018

  Решение задания 13 ЕГЭ 2021 по математике

  
  (47162)
  

• 
  10.10.2018

  Решение задания 14 ЕГЭ 2021 по математике

  
  (29180)
  

• 
  10.10.2018

  Решение задания 15 ЕГЭ 2021 по математике

  
  (51173)
  

• 
  10.10.2018

  Решение задания 16 ЕГЭ 2021 по математике

  
  (19521)
  

• 
  10.10.2018

  Решение задания 17 ЕГЭ 2021 по математике

  
  (41908)
  

• 
  10.10.2018

  Решение задания 18 ЕГЭ 2021 по математике

  
  (28448)
  

• 
  10.10.2018

  Решение задания 19 ЕГЭ 2021 по математике

  
  (19452)
  

• 
  20.11.2017

  Банковские задачи в ЕГЭ: подробное решение

  
  (10457)
  

• 
  20.11.2017

  Задания по планиметрии для ЕГЭ по математике

  
  (5778)
  

• 
  27.04.2017

  Нестандартные задания ЕГЭ 2017 по математике

  
  (6869)
  

• 
  21.02.2017

  Прототипы задач с пирамидой из ЕГЭ по математике

  
  (6678)
  

• 
  05.02.2017

  Прототипы заданий по теории вероятности

  
  (8123)
  

• 
  03.02.2017

  Прототипы задания 13 ЕГЭ по математике

  
  (26058)
  

• 
  11.04.2016

  Сборник тригонометрических уравнений с показательной функцией для ЕГЭ по математике

  
  (7894)
  

• 
  11.04.2016

  Сборник тригонометрических уравнений с логарифмами для ЕГЭ по математике

  
  (11150)
  

• 
  11.04.2016

  Сборник тригонометрических уравнений с дробями для ЕГЭ по математике

  
  (5803)
  

• 
  14.03.2016

  15 заданий по теории вероятности, ЕГЭ по математике

  
  (8349)
  

• 
  14.03.2016

  Тренировочная работа по заданиям 13-17 ЕГЭ по математике

  
  (8646)
  

• 
  14.03.2016

  Сборник текстовых задач ЕГЭ по математике (с ответами)

  
  (8444)
  

• 
  24.01.2016

  Задания по теории вероятности для ЕГЭ по математике

  
  (22979)
  

• 
  24.01.2016

  «Логарифмические уравнения»: тренировочные тесты ЕГЭ по математике

  
  (12716)
  

• 
  14.01.2016

  Тренажёр ЕГЭ по математике (профильный уровень)

  
  (18005)
  

• 
  02.01.2016

  Задания по производной, ЕГЭ по математике

  
  (10079)
  

• 
  02.01.2016

  Сборник задач с параметрами для ЕГЭ по математике

  
  (6314)
  

• 
  02.01.2016

  Сборник задач по тригонометрии для ЕГЭ по математике

  
  (6551)
  

• 
  02.01.2016

  Сборник задач по планиметрии для ЕГЭ по математике

  
  (15590)
  

• 
  02.01.2016

  Сборник задач по экономике для ЕГЭ по математике

  
  (7362)
  

• 
  02.01.2016

  Сборник заданий 13 ЕГЭ 2016 по математике с ответами

  
  (8309)
  

• 
  27.11.2015

  Задачник ЕГЭ по тригонометрии (с ответами и решениями)

  
  (23495)
  

• 
  09.11.2015

  Графики и диаграммы, ЕГЭ по математике

  
  (4998)
  

• 
  09.11.2015

  Задачи на координатной плоскости, ЕГЭ по математике

  
  (4291)
  

• 
  09.11.2015

  Наименьшее и наибольшее значения функции, точки экстремума, ЕГЭ по математике

  
  (5389)
  

• 
  09.11.2015

  Комбинации фигур (планиметрия) — ЕГЭ по математике

  
  (4424)
  

• 
  09.11.2015

  Задачи по планиметрии — ЕГЭ по математике

  
  (5071)
  

• 
  09.11.2015

  Трапеция, параллелограмм, ромб — ЕГЭ по математике

  
  (4678)
  

• 
  09.11.2015

  Треугольник, квадрат, прямоугольник — ЕГЭ по математике

  
  (4046)
  

• 
  09.11.2015

  Площадь круга — ЕГЭ по математике

  
  (3836)
  

• 
  09.11.2015

  Найти площадь фигуры — ЕГЭ по математике

  
  (4561)
  

• 
  09.11.2015

  Преобразование выражений — ЕГЭ по математике

  
  (4352)
  

• 
  09.11.2015

  Прикладные задачи — ЕГЭ по математике

  
  (4078)
  

• 
  09.11.2015

  Прогрессия — ЕГЭ по математике

  
  (3904)
  

• 
  09.11.2015

  Производная и первообразная — ЕГЭ по математике

  
  (6504)
  

• 
  09.11.2015

  Простые вычисления — ЕГЭ по математике

  
  (3950)
  

• 
  09.11.2015

  Задачи на проценты с округлением — ЕГЭ по математике

  
  (3588)
  

• 
  09.11.2015

  Округление с недостатком — ЕГЭ по математике

  
  (3205)
  

• 
  09.11.2015

  Округление с избытком — ЕГЭ по математике

  
  (3404)
  

• 
  09.11.2015

  Задачи на проценты — ЕГЭ по математике

  
  (5177)
  

• 
  09.11.2015

  Прямоугольный треугольник — ЕГЭ по математике

  
  (3634)
  

• 
  09.11.2015

  Задачи на смеси, сплавы, растворы — ЕГЭ по математике

  
  (5796)
  

• 
  09.11.2015

  Комбинации тел (стереометрия) — ЕГЭ по математике

  
  (12013)
  

• 
  09.11.2015

  Конус и цилиндр (стереометрия) — ЕГЭ по математике

  
  (6155)
  

• 
  09.11.2015

  Многогранники (стереометрия) — ЕГЭ по математике

  
  (12503)
  

• 
  09.11.2015

  Параллелепипед и куб (стереометрия) — ЕГЭ по математике

  
  (4516)
  

• 
  09.11.2015

  Пирамиды (стереометрия) — ЕГЭ по математике

  
  (4204)
  

• 
  09.11.2015

  Призма (стереометрия) — ЕГЭ по математике

  
  (4527)
  

• 
  09.11.2015

  Шар (стереометрия) — ЕГЭ по математике

  
  (4263)
  

• 
  09.11.2015

  Теория вероятности — ЕГЭ по математике

  
  (7477)
  

• 
  09.11.2015

  Треугольники — ЕГЭ по математике

  
  (5180)
  

• 
  09.11.2015

  Угол на листе в клетку — ЕГЭ по математике

  
  (3510)
  

• 
  09.11.2015

  Вписанный угол — ЕГЭ по математике

  
  (3397)
  

• 
  09.11.2015

  Выбор оптимального варианта — ЕГЭ по математике

  
  (3795)
  

• 
  09.11.2015

  Задачи на движение — ЕГЭ по математике

  
  (4917)
  

• 
  09.11.2015

  Задачи на работу — ЕГЭ по математике

  
  (3625)
  

• 
  09.11.2015

  Задачи с векторами — ЕГЭ по математике

  
  (7188)
  

• 
  12.07.2015

  Типовые задания 19 ЕГЭ 2015 по математике с ответами

  
  (4703)
  

• 
  17.05.2015

  Ве задачи №19 (экономические) с ответами и решениями, ЕГЭ 2015 по математике

  
  (7053)
  

• 
  02.05.2015

  Сборник заданий 15, 16, 17, 18 ЕГЭ 2015 по математике (с ответами)

  
  (5891)
  

• 
  02.05.2015

  Задание 14 ЕГЭ 2015 по математика: задания с ответами

  
  (5400)
  

• 
  02.05.2015

  Задание 8 ЕГЭ 2015 по математика: задания с ответами

  
  (4059)
  

• 
  02.05.2015

  Тренировочные задания 1-14 ЕГЭ по математике с решениями и ответами

  
  (5607)
  

• 
  01.04.2015

  Прототипы заданий ЕГЭ по математике базового уровня

  
  (19576)
  

• 
  31.03.2015

  Прототипы заданий ЕГЭ по математике с ответами и решниями

  
  (22786)
  

• 
  31.03.2015

  Задание 7 ЕГЭ по математике (с ответами)

  
  (4088)
  

• 
  29.01.2015

  Задание 10 ЕГЭ по математике с решениями и ответами

  
  (4506)
  

• 
  12.09.2014

  Задание 20 ЕГЭ 2015 по математике

  
  (6292)
  

• 
  09.09.2014

  Задание 18 ЕГЭ 2015 по математике

  
  (6135)
  

• 
  05.08.2014

  Алгебра — задания ЕГЭ по математике

  
  (7188)
  

• 
  05.08.2014

  Функции — задания ЕГЭ по математике

  
  (4851)
  

• 
  05.08.2014

  Геометрия — задания ЕГЭ по математике

  
  (8939)
  

• 
  05.08.2014

  Элементы комбинаторики и теории вероятностей — задания ЕГЭ по математике

  
  (7789)
  

• 
  05.08.2014

  Математический анализ — задания ЕГЭ по математике

  
  (5321)
  

• 
  05.08.2014

  Уравнения и неравенства — задания ЕГЭ по математике

  
  (6608)
  

• 
  15.05.2014

  Решение и ответы заданий В5 ЕГЭ по математике — площади многоугольников

  
  (5124)
  

• 
  15.05.2014

  Решение заданий В5 ЕГЭ по математике — площади частей круга

  
  (5033)
  

• 
  15.05.2014

  Решение заданий В1, В2 из ЕГЭ по математике 2014 год

  
  (5939)
  

• 
  15.05.2014

  Решение всех типов задания С3 из ЕГЭ 2013 по математике

  
  (5732)
  

• 
  15.05.2014

  Решение всех типов задания С2 из ЕГЭ 2012 по математике

  
  (5560)