Смещение груза пружинного маятника от положения равновесия меняется с течением времени по закону где период Т = 1 с. Через какое минимальное время начиная с момента t = 0 потенциальная энергия маятника вернётся к своему исходному значению? Ответ выразите в секундах.
Спрятать решение
Решение.
Потенциальная энергия пружинного маятника зависит от квадрата смещения груза
В нулевой момент времени смещение груза Через
смещение груза будет равно
и потенциальная энергия вернется к своему исходному значению.
Ответ: 0,5.
Источник: ЕГЭ по физике. Вариант 114, ЕГЭ по физике 2022. Досрочная волна. Вариант 2
Версия для печати и копирования в MS Word
1
Период колебаний потенциальной энергии горизонтального пружинного маятника 1 с. Каким будет период ее колебаний, если массу груза маятника увеличить в 2 раза, а жесткость пружины вдвое уменьшить? (Ответ дайте в секундах.)
Ответ:
2
Период колебаний потенциальной энергии пружинного маятника 1 с. Каким будет период ее колебаний, если массу груза маятника и жесткость пружины увеличить в 4 раза? (Ответ дайте в секундах.)
Ответ:
3
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова полная механическая энергия маятника в момент времени, соответствующий на графике точке D? (Ответ дайте в джоулях.)
Ответ:
4
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова кинетическая энергия маятника в момент времени
? (Ответ дайте в джоулях.)
Ответ:
5
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова кинетическая энергия маятника в момент времени
? (Ответ дайте в джоулях.)
Ответ:
6
На рисунке дан график зависимости координаты материальной точки от времени. Какова частота колебаний? (Ответ дайте в герцах.)
Ответ:
7
Скорость тела, совершающего гармонические колебания меняется с течением времени в соответствии с уравнением где все величины выражены в СИ. Какова амплитуда колебаний скорости? (Ответ дайте в метрах в секунду.)
Ответ:
8
Колебательное движение тела задано уравнением:
где
Чему равна амплитуда колебаний? (Ответ дайте в сантиметрах.)
Ответ:
9
Груз, подвешенный на пружине жёсткостью совершает свободные гармонические колебания. Какой должна быть жёсткость пружины, чтобы частота колебаний этого груза увеличилась в 2 раза? (Ответ дайте в ньютонах на метр.)
Ответ:
10
На рисунке изображена зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Какова амплитуда колебаний этого маятника при резонансе? (Ответ дайте в сантиметрах.)
Ответ:
11
На графиках представлена зависимость координаты х центров масс тела а и тела б от времени t при гармонических колебаниях вдоль оси Ox.
На каком расстоянии друг от друга находятся центры масс тел а и б в момент времени 0 с? (Ответ дайте в сантиметрах.)
Ответ:
12
На рисунке представлены графики зависимости координаты х центров масс тела а и тела б от времени t при гармонических колебаниях вдоль оси Ox.
На каком расстоянии друг от друга находятся центры масс тел а и б в момент времени ? (Ответ дайте в сантиметрах.)
Ответ:
13
На рисунке представлены графики зависимости координаты х центров масс тела а и тела б от времени t при гармонических колебаниях вдоль оси Ox.
В какой момент времени между 0 и 4 с тело б двигалось в том же направлении и с такой же скоростью, которую имело тело а в момент времени ? (Ответ дайте в секундах.)
Ответ:
14
Гиря массой 4 кг, подвешенная на стальной пружине, совершает свободные колебания с периодом 2 с. С каким периодом будет совершать свободные колебания гиря массой 1 кг, подвешенная на этой пружине? (Ответ дайте в секундах.)
Ответ:
15
При свободных колебаниях груза на нити математического маятника его кинетическая энергия изменяется от 0 Дж до 50 Дж, максимальное значение потенциальной энергии 50 Дж. Чему равна полная механическая энергия груза при таких колебаниях? (Ответ выразите в джоулях.)
Ответ:
16
В таблице представлены данные о положении шарика, гармонически колеблющегося вдоль оси Ox в различные моменты времени.
| t, с | 0,0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| х, мм | 0 | 2 | 5 | 10 | 13 | 15 | 13 | 10 | 5 | 2 | 0 | –2 | –5 | –10 | –13 | –15 | –13 |
Какова амплитуда колебаний шарика? (Ответ дайте в миллиметрах.)
Ответ:
17
Груз массой 50 г, прикреплённый к лёгкой пружине, совершает свободные колебания. График зависимости координаты x этого груза от времени t показан на рисунке. Чему равна жёсткость пружины?
Ответ:
18
Маленький грузик, закреплённый на пружине жёсткостью 80 Н/м, совершает гармонические колебания. График зависимости координаты x этого грузика от времени t изображён на рисунке. Какова масса грузика? (Ответ дайте в граммах.)
Ответ:
19
Частота собственных малых вертикальных колебаний пружинного маятника равна 6 Гц. Какой станет частота таких колебаний, если массу груза пружинного маятника увеличить в 4 раза? Ответ приведите в герцах.
Ответ:
20
Груз на длинной лёгкой пружине совершает колебания с частотой 0,5 Гц. Пружину разрезали на 4 равные части и прикрепили к одной из частей тот же груз. Чему стал равен период колебаний получившегося пружинного маятника? (Ответ дайте в секундах.)
Ответ:
21
Груз подвешен на лёгкой вертикальной пружине и совершает на ней колебания с частотой ω = 10 рад/с, двигаясь по вертикали. На какую длину растянется эта пружина, если аккуратно подвесить к ней тот же груз, не возбуждая колебаний? (Ответ дайте в сантиметрах.) Ускорение свободного падения принять равным 10 м/с2.
Ответ:
22
На рисунке изображена зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Частота вынуждающей силы вначале была равна 0,5 Гц, а затем стала равна 1,0 Гц.
Во сколько раз изменилась при этом амплитуда установившихся вынужденных колебаний маятника?
Ответ:
23
Гиря массой 2 кг подвешена на стальной пружине и совершает свободные колебания вдоль вертикально направленной оси Ox, координата x центра масс гири, выраженная в метрах, изменяется со временем по закону Чему равна кинетическая энергия гири в начальный момент времени? (Ответ выразите в джоулях.)
Ответ:
24
Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили без начальной скорости (см. рис.). Через какое время (в долях периода) после этого кинетическая энергия маятника в первый раз достигнет минимума? Сопротивлением воздуха пренебречь.
Ответ:
25
Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили с начальной скоростью, равной нулю (см. рисунок). Через какое время (в долях периода) после этого потенциальная энергия маятника в первый раз вновь достигнет максимума? Сопротивлением воздуха пренебречь.
Ответ:
26
Математический маятник с периодом колебаний Т отклонили на небольшой угол от положения равновесия и отпустили с начальной скоростью равной нулю (см. рисунок). Через какое время (в долях периода) после этого кинетическая энергия маятника во второй раз достигнет максимума? Сопротивлением воздуха пренебречь.
Ответ:
27
Точечное тело совершает гармонические колебания, двигаясь вдоль прямой линии. Школьник построил график зависимости координаты x этого тела от времени t (показан на рисунке). Чему равна максимальная скорость движения тела? Ответ выразите в метрах в секунду.
Ответ:
28
Груз, закреплённый на лёгкой пружине жёсткостью 200 Н/м, совершает вертикальные колебания. На рисунке изображены графики зависимости смещения x груза от времени t и проекции Vx скорости груза от времени. Определите, чему равна масса груза. Ответ выразите в килограммах.
Ответ:
29
Математический маятник, колеблющийся с циклической частотой ω = 3 с−1, в нижней точке траектории имеет ускорение, равное по модулю a = 1 м/с2. Масса груза маятника m = 900 г. Чему равен запас механической энергии маятника?
Ответ:
30
Длина нити математического маятника при проведении первого опыта была равна 40 см, а при проведении второго опыта — 10 см. Во сколько раз увеличилась частота колебаний математического маятника при проведении второго опыта?
Ответ:
31
Груз, подвешенный на пружине жесткости 400 Н/м, совершает вертикальные свободные гармонические колебания. Какой должна быть жесткость пружины, чтобы частота колебаний этого же груза была в 2 раза меньше.
Ответ:
32
Смещение груза пружинного маятника от положения равновесия меняется с течением времени по закону где период Т = 1 с. Через какое минимальное время начиная с момента t = 0 потенциальная энергия маятника вернётся к своему исходному значению? Ответ выразите в секундах.
Ответ:
33
Период свободных колебаний пружинного маятника равен 0,5 с. Каким станет период свободных колебаний этого маятника, если массу груза маятника увеличить в 2 раза, а жёсткость пружины вдвое уменьшить? Ответ дайте в секундах.
Ответ:
34
Шарик массой 0,4 кг, подвешенный на пружине, совершает свободные гармонические колебания вдоль вертикальной прямой. Какой должна быть масса шарика, чтобы период его свободных вертикальных гармонических колебаний на этой же пружине был в 2 раза меньше?
Ответ:
35
Груз, подвешенный на лёгкой пружине жёсткостью 400 Н/м, совершает свободные вертикальные гармонические колебания. Пружину какой жёсткости надо взять вместо первой пружины, чтобы период свободных колебаний этого груза стал в 2 раза меньше? Ответ приведите в ньютонах на метр.
Ответ:
36
Груз массой 0,16 кг, подвешенный на пружине, совершает свободные вертикальные гармонические колебания. Груз какой массой нужно подвесить вместо первого груза, чтобы частота свободных колебаний уменьшилась в 2 раза? Ответ приведите в килограммах.
Ответ:
37
Первый математический маятник совершает 30 колебаний за 20 с, а второй математический маятник совершает 60 колебаний за 80 с. Во сколько раз длина второго маятника больше длины первого? Ответ:_______________________ раз(-а).
Ответ:
38
Изменение координаты при движении маятника имеет вид Период колебаний маятника равен Т = 2 с. Через какое время кинетическая энергия маятника впервые примет минимальное значение? Ответ дайте в секундах.
Ответ:
39
Во сколько раз уменьшится частота малых свободных колебаний математического маятника, если длину нити увеличить в 4 раза, а массу груза уменьшить в 5 раз?
Ответ:
40
Школьник проводил опыты с двумя разными пружинами. К первой пружине он подвесил гирьку массой 200 г, а ко второй пружине — гирьку массой 100 г. Оказалось, что обе пружины растянулись на одинаковую величину. Найдите, чему равно отношение периода колебаний первого груза на первой пружине к периоду колебаний второго груза на второй пружине. Трение отсутствует.
Ответ:
41
В научном институте стоит в шкафу математический маятник. Представим себе, что учёные сначала измерили период T1 колебаний этого маятника на Земле, а затем — период T2 колебаний этого же маятника на Луне.
Чему равно отношение Ускорение свободного падения на Луне равно 1,6 м/с2, сопротивлением воздуха на Земле можно пренебречь.
Ответ:
42
Смещение груза пружинного маятника меняется с течением времени где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, кинетическая энергия маятника достигнет минимального значения?
Ответ выразите в секундах.
Ответ:
43
Какую длину должен иметь математический маятник для того, чтобы период его колебаний был таким же, как у пружинного маятника с грузом массой 0,2 кг, подвешенного на пружине жёсткостью 20 Н/м? Ответ дайте в сантиметрах.
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
Фото: СеверПост / Анна Шепеткова
«Спуститься» в подземный рудник и «прогуляться» по карьеру. Узнать, как правильно презентовать себя, не промахнуться с выбором специальности и попасть в компанию мечты. Ответы на эти вопросы получили заполярные школьники, а также их родители в рамках «Дня с ФосАгро». Подробности — в репортаже СеверПост.
Из «научки» — в рудник
Выездной день открытых дверей компании «ФосАгро» и апатитского филиала Мурманского Арктического государственного университета (МАГУ) состоялся 11 марта в областной научной библиотеке.
В профориентационном мероприятии «День с ФосАгро» участвовало более 300 старшеклассников из столицы Заполярья, Колы и Североморска, их родителей и педагогов.
Задача — познакомить школьников с ключевым партнёром вуза — компанией «ФосАгро», помочь определиться со специальностью и грамотно выстроить свою личную траекторию успеха.
Школьники с энтузиазмом откликнулись на приглашение. Благодаря этому на четыре часа главное книгохранилище региона превратилось в гудящий улей.
«Подарите обнимашки трём людям», — с такого задания от активистов волонтёрского движения «Команда» филиала МАГУ в г. Апатиты начался день.
А далее последовала экскурсия по залам и закрытой части книгохранилища научной библиотеки.
«Помимо миллиона книг и документов, позволяющих готовиться к ЕГЭ, наша библиотека — это место, где можно отдохнуть. Вы знали, что в зале искусств есть огромное количество бесплатных настольных игр и игровая пристаавка? Слышали, что в декабре у нас открылся новый зал развития, где проходят мастер-классы по каллиграфии и встречаются члены клуба разговорного английского языка?» — сыпал вопросами гид.
Дальше было столько активностей, что обойдёмся кратким списком.
Старшеклассники играли в дженгу, участвовали в квесте, квизах, тренингах по самопрезентации. Подростки пробовали себя в других формах интерактивного взаимодействия, а также узнали, как стать частью команды Кировского филиала АО «Апатит», получив высшее образование в филиале МАГУ в Апатитах.
Без внимания не остался никто из присутствующих. Небольшая очередь выстроилась у аудитории с табличкой «In ФосАгро», где гостям было предложена виртуальная прогулка по Кировскому, Расвумчоррскому или Восточному рудникам.
Из Сирии за мечтой
С каждым годом апатитский филиал МАГУ становится всё более манящим «центром притяжения». В настоящее время в кузнице кадров для горно-обогатительного производства обучаются студенты со всего Кольского полуострова, но есть гости и издалека.
Молодой человек Алаа Хурия прибыл в Апатиты из Дамаска — второго по величине города в Сирии.
Вместе со своими однокурсниками он принял участие в круглом столе на тему «Быть студентом: инструкция по выживанию». Там в форме оживлённого диалога с абитуриентами и родителями юноша дал исчерпывающую информацию по всем волнующим их вопросам.
Алаа Хурия рассказал, что на Кольский полуостров приехал минувшей осенью и предварительно год учил «великий и могучий» на подготовительных курсах.
Сравнивая Россию и Сирию, он говорит, что в его стране снег бывает 3-4 дня за год и что к холоду невозможно привыкнуть, но тепло и радушие северян не позволяют ему замёрзнуть.
«Ещё в школе я мечтал изучать информационные системы, поэтому выбрал специальность «Информационные системы и технологии», — поведал молодой человек.
Ему нравится Апатиты. По его словам, это красивый город с хорошими людьми. За время учёбы у него появилось много приятелей. Кроме того, иностранец по достоинству оценил русский борщ и оливье.
«Я чувствую себя здесь, как дома. Здесь мне даже лучше, чем в Москве, где я жил у своего родственника и изучал русский язык на подготовительных курсах. Я хочу здесь работать, потому в будущем рассматриваю для трудоустройства компанию «ФосАгро», так как она предоставляет большие возможности для построения карьеры», — «миксует» русские слова с английскими Алаа.
Как зачётка может приносить деньги
Разобраться в направлениях, ознакомиться с правилами поступления и поощрения прилежных студентов будущим абитуриентам помогали работники приёмной комиссии университета.
Так, в рамках презентации «МАГУ-Апатиты» специалист приёмной комиссии Семён Ставцев поделился со школьниками лайфхаками, как превратить пятёрки в зачётке в 10, 40 и даже в 100 тысяч рублей.
«До первой сессии все первокурсники получают 6 000 рублей, по итогам сессии, если сдал без троек, то 8 000, отличники — 12 000 рублей. Кроме того, есть стипендия за особые достижения — 14 000. Стипендия «ФосАгро» — это ещё 10 000, стипендия старост составляет от 2 до 10 000. Плюс ещё существует социальная стипендия — 10 000 — обычная, 14 000 — повышенная. Суммы суммируются. Чем больше результатов в науке, спорте или общественной жизни, тем выше конечная сумма стипендии. В среднем я получал, обучаясь в вузе, 40 000. Под Новый год моя стипендия составила 100 000, и это реально», — сообщил Семён.
При этом, как подчёркивают в приёмной комиссии, вуз постоянно совершенствует образовательный процесс, расширяя список специальностей и направлений.
«Особое внимание заслуживает направление подготовки «Ядерная энергетика и теплофизика», ведь наш факультет один из немногих в стране, где выделены бюджетные места на это направление», — говорит Ставцев.
При этом члены приёмной комиссии акцентируют внимание на том, что поступление на бюджет апатитского филиала МАГУ — это не миф, набор проводится ежегодно.
Добавим, что в апатитском филиале вуза студенты не только бесплатно осваивают востребованные профессии, но и обеспечиваются общежитием на территории вуза, плата за которое составляет 690 рублей в месяц. Кроме того, они проходят оплачиваемую практику.
«За нашими выпускниками выстраивается очередь»
«Поступить к нам не так сложно, как в столичные вузы. При этом инженерные кадры сейчас очень востребованы. Кадровый голод испытывают все ведущие предприятия Мурманской области. За нашими выпускниками буквально очередь выстраивается уже на старших курсах, и мы способствуем трудоустройству студентов 3-4 курсов. Построить карьеру в апатитском филиале МАГУ можно по двум векторам: производственному или академическому», — рассказал начальник отдела карьерного сопровождения филиала МАГУ г. Апатиты Илья Балымов.
Как отметил Балымов, среди студентов филиала немало выдающихся личностей — обладателей всевозможных престижных «трофеев», а также стипендий губернатора и президента.
Так, студент апатитского филиала МАГУ по направлению подготовки «Информационные системы и технологии» Роман Воронин собрал все самые престижные стипендии, а за победу на национальном водном конкурсе, где он представил свою научную работу, два года назад он отправился в поездку на Северный полюс на атомном ледоколе «50 лет Победы».
Студенты признаются: не только учёбой интересен их филиал.
«Наш университет не только даёт профессию, но и всесторонне развивает молодёжь. Совет поступающим могу дать только один: выбирайте сердцем, ведь это решение во многом предопределяет развитие не только карьеры, но и судьбы человека», — рассказал студент-второкурсник направления «Физические процессы горного и нефтегазового производства» Василий.
Будущие студенты, в свою очередь, были готовы тотчас приступить к учёбе.
«Спасибо организаторам за эту встречу. Сегодня я задумался о том, чтобы поступить учиться в апатитский филиал МАГУ, ведь, как оказалось, чтобы получить компетентные знания и навыки по интересующей меня геологии, совсем не нужно покидать родной регион. Впечатлили меня и социальные гарантии работникам «ФосАгро»», — поделился впечатлениями десятиклассник мурманской гимназии №7 Михаил Сухов.
Добавим несколько деталей. Руководство компании подчёркивает: их коллективный договор является одним из лучших по Северо-Западу.
«Нашим работникам мы предоставляем «подъемные», большие отпуска — от 52 до 90 дней, раз в два года сотрудникам и членам семьи оплачивается проезд к месту отдыха и обратно, в том числе и за границу. Иногородним специалистам компенсируется аренда жилья. Кроме того, регулярно предоставляются путёвки в дома отдыха и санатории, а также детские лагеря. Помимо этого, предусмотрены выплаты к рождению детей, к заключению брака и другие», — рассказала о социальных гарантиях руководитель проекта «Кадры для ФосАгро» Мария Заречённая.
По словам Марии, компания предоставляет беспрецедентные возможности для раннего трудоустройства и комфортных условий труда своих сотрудников. Человеческий капитал для «ФосАгро» — в приоритете.
Механика. Изменение физических величин в процессах
В. З. Шапиро
В этом задании нужно определить, как меняются физические величины в различных ситуациях. Темы могут варьироваться по всем разделам механики.
1. Подвешенный на пружине груз совершает свободные вертикальные гармонические колебания. Пружину заменили на другую, жёсткость которой меньше, оставив массу груза и амплитуду колебаний неизменными. Как при этом изменятся частота свободных колебаний груза и его максимальная скорость?
Для каждой величины определите соответствующий характер изменения
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Частота свободных колебаний груза | Максимальная скорость груза |
Период свободных колебаний пружинного маятника определяется по формуле Замена пружины на пружину с меньшей жёсткостью приведёт к росту периода. Так как
то частота колебаний уменьшится. Максимальная скорость груза определяется из закона сохранения и превращения механической энергии.
Скорость уменьшится.
Ответ: 22.
Форма вопросов в заданиях может быть различной. Но правильные ответы базируются на умении определять, как изменятся одни физические величины при изменении других.
- Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом потенциальная энергия спутника в поле тяжести Земли и его период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Потенциальная энергия |
Период обращения спутника вокруг Земли |
Эту задачу можно решить, используя простые рассуждения. Так как при переходе на другую орбиту скорость спутника уменьшилась, то его притяжение к Земле стало также меньше. Следовательно, он отдалился от поверхности Земли на большее расстояние. Радиус новой орбиты больше, поэтому потенциальная энергия увеличивается. Обращение вокруг Земли стало медленнее, поэтому период также возрастает.
Ответ: 11.
Секрет решения: Движение ИСЗ (искусственного спутника Земли) связано с притяжением Земли. В этой теме много сложных для запоминания формул. Выводы большинства этих формул основываются на знаниях закона всемирного тяготения и понятия центростремительной силы. Равенство силы всемирного тяготения и центростремительной силы позволяет упростить запоминание «тяжелых» формул.
3. На поверхности воды плавает брусок из древесины плотностью 500 кг/м3. Брусок заменили на другой брусок той же массы и с той же площадью основания, но изготовленный из древесины плотностью 700 кг/м3. Как при этом изменились глубина погружения бруска и действующая на него сила Архимеда?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Глубина погружения бруска |
Сила Архимеда |
Ключевым моментом в подобных задачах является равенство силы тяжести и силы Архимеда. При выполнении этого условия тела плавают на поверхности жидкости. Так как в обоих случаях масса не изменилась, то сила тяжести и сила Архимеда также не изменились.
Глубину погружения можно выразить из формулы для силы Архимеда.
Из последней формулы видно, что все физические величины остались без изменения. Поэтому глубина погружения не изменилась.
Ответ: 33.
Секрет решения: При рассмотрении задач на плавание тел надо приравнивать силу Архимеда и силу тяжести. Надо помнить, что в формуле для выталкивающей силы используется плотность жидкости (а не тела) и объем погруженной части тела (а не весь объем тела).
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 6 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 67.9%
Ответом к заданию 4 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
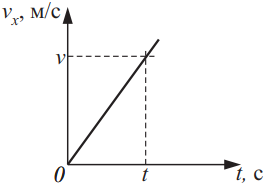
На рисунке изображён график зависимости проекции скорости тела массой m от времени (t). На основании графика выберите два верных утверждения из приведённого ниже списка для момента времени t. Укажите их номера.
- Движущаяся сила вычисляется по формуле F = m · v · t.
- Работу силы можно найти по формуле $A = {m· v}/{2t}$.
- Движущаяся сила вычисляется по формуле $F = {mv}/{t}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2t^2}$.
Решение
3) Движущаяся сила $F=ma$, где $a={υ-υ_0}/{y}={υ}/{t}$, поскольку $υ_0=0$, что видно графика. Тогда $F=ma={mυ}/{t}$.
4) Работа силы равна изменению кинетической энергии, т.е. $A=∆E_к={mυ^2}/{2}-{mυ_0^2}/{2}$, поскольку $υ_0=0$, то $A={mυ^2}/{2}-0={mυ^2}/{2}$.
Ответ: 34
Задача 2
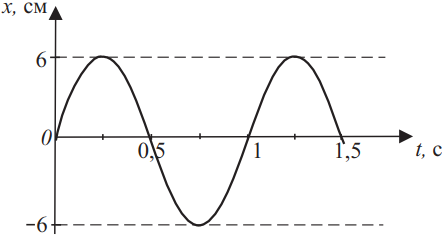
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
- Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
- Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение
1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{1}=2π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin({2π}/{T}·t)$. Подставим наши данные, имеем: $x=6·sin({2πt}/{1})=6·sin(2π·t)$. Координата колебания подчиняется закону синуса, следовательно, в момент времени, равный 10 периодам колебаний, тело находится в точке с координатой $х=0$ см.
Ответ: 35
Задача 3
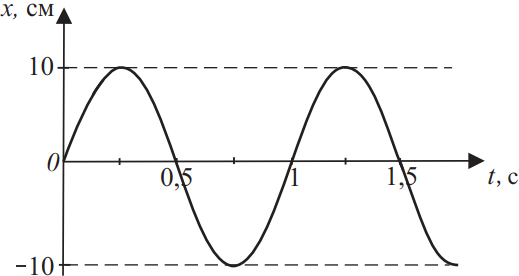
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- Период колебаний тела равен 1 с.
- Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
- Тело совершает колебания с периодом 0,1 с.
- Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).
Решение
1) Из графика видно, что период колебаний тела равен 1с.
4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см — амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.
Ответ: 14
Задача 4
Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, м | 0 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 |
- Коэффициент упругости пружины равен 2,5 Н/м.
- При увеличении массы груза растяжение пружины уменьшается.
- Потенциальная энергия пружины пропорциональна растяжению пружины.
- Потенциальная энергия пружины при её растяжении на 0,08 м равна 0,08 Дж.
- При подвешенном к пружине грузе массой 100 г её удлинение составит 4 см.
Решение
Исходя из теории упругости и результатов опыта, определим $E_n={kx^2}/{2}={25·0.08^2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
Ответ: 45
Задача 5
Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
| t, c | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| x, см | 6 | 3 | 0 | 3 | 6 | 3 | 0 | 3 |
- Максимальная скорость грузика равна 0,15 м/с.
- Период колебаний шарика равен 0,4 с.
- В момент времени 0,1 с кинетическая энергия шарика максимальна.
- Полная механическая энергия шарика остаётся неизменной.
- Амплитуда колебаний шарика равна 6 мм.
Решение
Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 — верно).
Период колебании — время за которое происходит одно полное колебание — 0,4 с (2 — верно)
Максимальная скорость шарика связана с амплитудой ( $υ_{max}=А ω ={А2π}/{T}= {0,03* 2*3.14}/{0,4}=0,471$м/с. (1 — неверно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 — верно)
Амплитуда колебания — это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 — неверно)
Ответ: 234
Задача 6
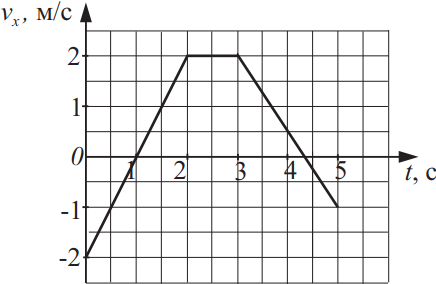
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.
- В течение первых двух секунд перемещение тела равно 2 м.
- Модуль ускорения тела в промежутке времени от 1 с до 2 с на 25% больше модуля ускорения тела в промежутке времени от 3 с до 4 с.
- В течение первой секунды кинетическая энергия тела увеличилась на 30 Дж.
- В промежутке времени от 1 с до 2 с импульс тела увеличился в 2 раза.
- В момент времени 4 с модуль равнодействующей сил, действующих на тело, равен 22,5 Н.
Решение
Из теории кинематики и данного графика можно сказать, что модуль ускорения тела с 1 до 2 на 25% больше 3-4, т.е. $a_{1-2}=2м/с^2; a_{3-4}=1.5м/с^2$. В момент времени 4с модуль равнодействующих сил, $F=22.5H$, т.к. $a_4=1.5м/с^2$, $F_p=ma_4=15·1.5=22.5H$
Ответ: 25
Задача 7
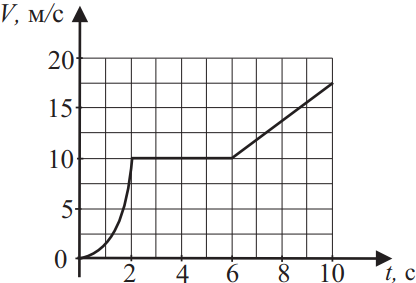
На рисунке представлен график зависимости скорости V от времени t для тела, движущегося прямолинейно. Используя данные графика, выберите из приведённого ниже списка все верные утверждения и укажите их номера.
- Первые две секунды тело двигалось равноускоренно.
- Со 2-й по 6-ю секунду тело переместилось на 40 м.
- Со 2-й по 6-ю секунду тело переместилось на меньшее расстояние, чем за первые две секунды.
- Средняя скорость тела во время движения со 2-й по 10-ю секунду равна 12,5 м/с.
- С 6-й по 10-ю секунду тело двигалось равноускоренно.
Решение
1) Неверно, так как равноускоренному движению соответствует линейный график: $v(t)=v_0+at$.
2)Верно. Из данного рисунка видно, что с 2 по 6 сек, тело прошло 40 м (площадь под графиком)
3) Неверно. Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.
4)Чтобы найти среднюю скорость, нужно разделить весь путь со 2-й по 10-ю секунду на всё соответствующее время, т.е. на 8 с. При этом путь определяем как площадь под графиком, так как у нас есть график в координатах v(t):
$S=S_1+S_2=8·10+{4·7,5}/2=110$ м.
Тогда $v_{ср}={110}/8=13,75$. Утверждение 4 — неверно.
5) Верно. С 6 по 10 сек, тело двигалось равноускоренно, т.к. за равные промежутки времени скорость увеличивается на одну ту же величину (линейная зависимость v(t)).
Ответ: 25
Задача 8

Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.
- За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
- При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
- В точке О кинетическая энергия маятника максимальна.
- Расстояние АБ соответствует амплитуде колебаний координаты.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
- За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ — «туда и обратно». 1 — неверно.
- При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 — неверно
- В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью — верно
- Амплитуда колебаний координаты — это половина расстояния АБ — отклонение от положения равновесия. 4 — неверно.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 — верно.
В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.
Ответ: 35
Задача 9
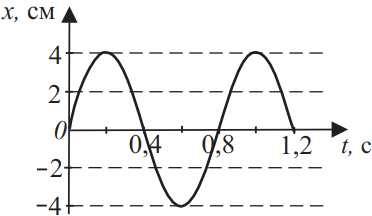
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Период колебаний тела равен 1 с.
- Амплитуда колебаний равна 8 см.
- Частота колебаний равна 1,25 Гц.
- Амплитуда колебаний равна 4 см.
- Период колебаний тела равен 0,4 с.
Решение
Из данного графика очевидно, что $A=4$см (2 — неверно, 4 — верно), период колебаний T=0.8 c (1, 5 — неверно), а частота $v={1}/{T}={1}/{0.8}=1.25$Гц.(3 — верно)
Ответ: 34
Задача 10
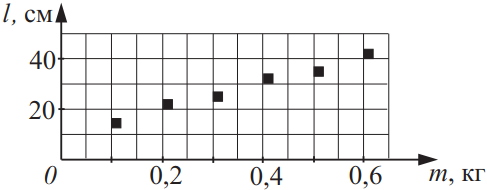
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.
- Коэффициент упругости пружины примерно равен 20 Н/м.
- Коэффициент упругости пружины примерно равен 30 Н/м.
- Коэффициент упругости пружины примерно равен 50 Н/м.
- Коэффициент упругости пружины примерно равен 10 Н/м.
- Для данного эксперимента выполняется закон Гука.
Решение
$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/м
Ответ: 15
Задача 11
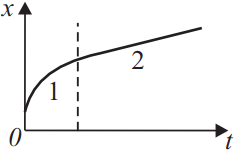
Бусинка скользит по неподвижной горизонтальной спице. На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
- На участке 1 проекция ускорения ax бусинки отрицательна.
- На участке 1 модуль скорости остаётся неизменным, а на участке 2 — уменьшается.
- На участке 1 модуль скорости увеличивается, а на участке 2 — уменьшается.
- На участке 1 модуль скорости уменьшается, а на участке 2 — остаётся неизменным.
- В процессе движения вектор скорости бусинки менял направление на противоположное.
Решение
Скорость — это производная координаты по времени. Графически это $tgα$ наклонной графика зависимости координаты от времени. Заметим, что координата все время растет, но на участке 1 — скорость уменьшается, следовательно, проекция ускорения отрицательна. На участке 2, скорость неизменна, а координата растет, тело не меняет направление движения.
Ответ: 14
Задача 12
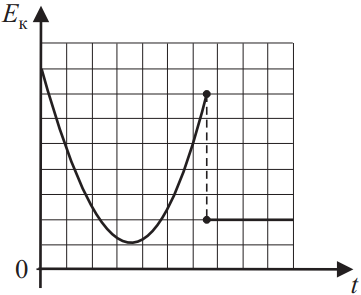
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
- В конце наблюдения кинетическая энергия тела равна нулю.
- Кинетическая энергия тела в течение всего времени наблюдения увеличивается.
- Кинетическая энергия тела в начальный момент времени максимальна.
- Тело брошено вертикально вверх с балкона и упало на Землю.
- В конце наблюдения скорость тела не равна нулю.
Решение
1) В конце наблюдения $E_к=0$, неверно, т.к. при $t=t_к⇒E_к≠0$, если $E_к=0$, то график должен проходить через ось ординат.
2) $E_к$, в течении всего времени увеличивается, неверно, т.к. при $t={t_к}/{2}$ $E_к=min$, в середине пути кинетическая энергия минимальна.
3) Исходя из графика $E_к$ максимальная в момент (верно) $t=0$.
4) Неверно, т.к. график вертикально брошенного тела, выглядит иначе.
5) При $t_к=t; E_к≠0$ (верно), т.к. $υ≠0⇔E_к≠0$.
Ответ: 35
Задача 13
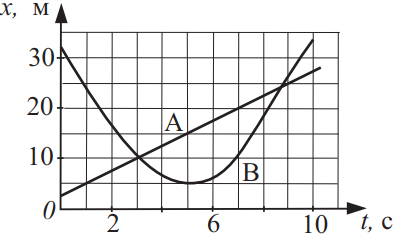
На рисунке приведены графики зависимости координаты от времени для двух тел A и B, движущихся по прямой, вдоль которой и направлена ось Ox. Из приведённого ниже списка выберите два верных утверждения о характере движения тел и укажите их номера.
- Тело A движется равномерно.
- Тело A движется с постоянным ускорением, равным 5 м/с2.
- Первый раз тела A и B встретились в момент времени, равный 3 с.
- Вторично тела A и B встретились в момент времени, равный 7 с.
- В момент времени t = 5 с тело B достигло максимальной скорости движения.
Решение
1) Тело А движется равномерно, т.к. равномерное движение — это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).
2) Ускорение тела А равно нулю, т.к. оно движется с постоянной скоростью $υ={20-10}/{7-3}=2.5м/с$ (не подходит).
3) Графики зависимости координаты от времени для двух тел А и В пересекаются в момент времени $t=3c$, значит, первый раз тела А и В встретились в момент времени, равный 3с (подходит).
Ответ: 13
Задача 14
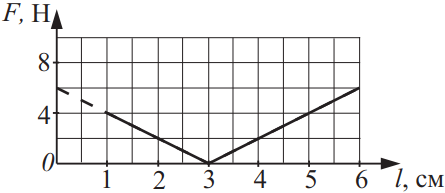
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.
- Длина пружины в недеформированном состоянии равна 6 см.
- Длина пружины в недеформированном состоянии равна 3 см.
- При действии силы 2 Н деформация пружины равна 2 см.
- При действии силы 4 Н деформация пружины равна 2 см.
- Коэффициент жёсткости пружины равен 50 Н/м.
Решение
1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).
2) Длина пружины в не деформированном состоянии равна 3 см (подходит).
3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).
4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).
Ответ: 24
Задача 15
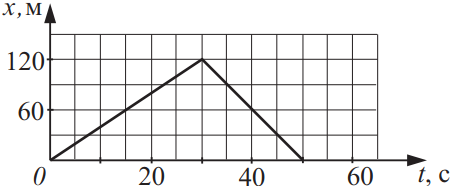
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения
- Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.
- Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
- Максимальная скорость движения на всём пути равна 2,4 м/с.
- За всё время движения тело прошло путь 120 м.
- За всё время движения тело прошло путь 240 м.
Решение
1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6м/с$. Знак «минус» говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2м/с$(подходит).
2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).
3) Максимальная скорость на всем пути равна 6м/с (не подходит).
4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).
5) За все время движения тело прошло путь 240м (подходит).
Ответ: 15
Задача 16
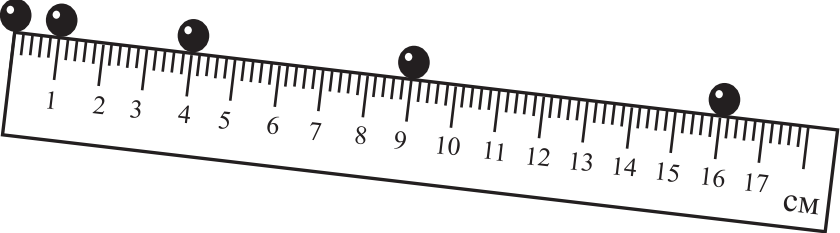
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Движение шарика равномерное.
- Скорость шарика увеличивается.
- Шарик движется под действием переменной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с, то его ускорение равно 0,5 см/с2.
- Импульс шарика в процессе движения остаётся постоянным.
Решение
1) Шарик за одинаковые промежутки времени проходит разные расстояния, значит, его движение неравномерное (не подходит).
2) Движение шарика равноускоренное, значит, скорость шарика увеличивается (подходит).
3) Шарик движется под действием постоянной силы $F↖{→}=ma↖{→}$ (не подходит).
4) $S=0.16м; t=4·2=8c; υ_0=0м/с; a=0.005м/с^2$. При равноускоренном движении перемещение равно: $S=υ_0е+{at^2}/{2}=0·8+{0.005·(8)^2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
Ответ: 24
Задача 17
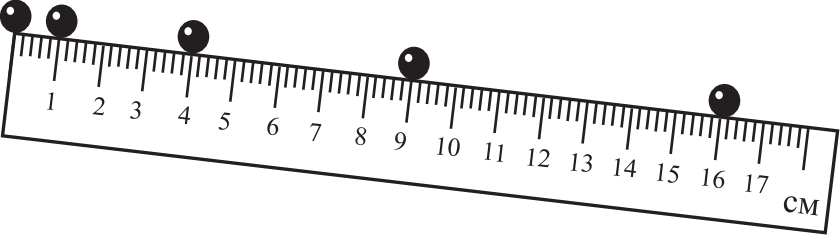
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Шарик движется с переменным ускорением.
- Скорость шарика уменьшается.
- Шарик движется под действием постоянной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с и он начинал движение из состояния покоя, то его скорость в точке с координатой 9 см равна 3 см/с.
- Импульс шарика в процессе движения уменьшается.
Решение
1) Шарик движется с постоянным ускорением (не подходит).
2) Скорость шарика увеличивается, т.к. за равные промежутки времени он проходит все больше расстояния (не подходит).
3) Шарик движется под действием постоянной силы $F=m·a$ (подходит).
4) $υ_k=υ_0+at$(1), т.к. $υ_0=0$м/с, поскольку начинает движение из состояния покоя, то $υ_k=at$(2). Перемещение $S={at^2}/{2}⇒a={2·S}/{t^2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).
Ответ: 34
Задача 18
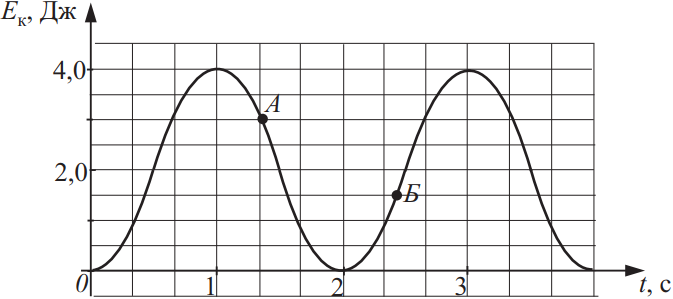
На рисунке приведён график зависимости кинетической энергии тела от времени t. Выберите все верные утверждения на основании анализа представленного графика.
- Тело движется под действием постоянной силы.
- Потенциальная энергия тела в точке Б равна 1,5 Дж.
- Период колебаний тела равен 4 с.
- Максимальное значение потенциальной энергии равно значению потенциальной энергии в точке А.
- Полная механическая энергия тела равна 4 Дж.
Решение
1. Из графика видно, что время одного полного колебания равно 4с, т.к. в течение одного полного колебания тело проходит три максимальных значения (или три минимальных значения) кинетической энергии, т.е. период колебаний тела равен 4с (верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{к,max}=E_{к,max}=E_к+Е_п$(1), а максимальная кинетическая энергия тела равна 4 Дж, то полная механическая энергия тела равна 4 Дж (верно).
Ответ: 35
Задача 19
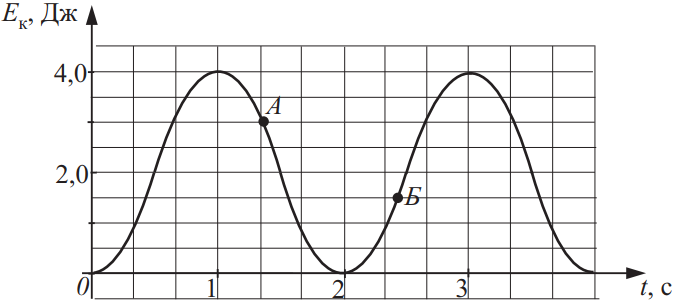
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает гармонические колебания.
- Потенциальная энергия тела в точке A равна 1 Дж.
- Период колебаний тела равен 2 с.
- Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
- Частота колебаний тела равна 4 Гц.
Решение
1. Тело совершает гармонические колебания, т.к. гармонические колебания — это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 — верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ — кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ — потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 — верно)
3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 — неверно)
4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 — неверно)
5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 — неверно)
Ответ: 12
Задача 20
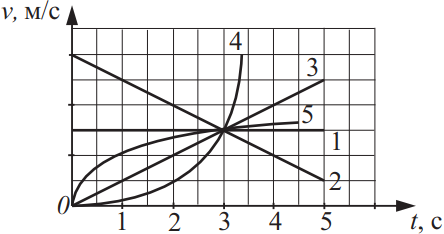
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленных графиков и укажите их номера.
- Наибольшей начальной скоростью обладало второе тело.
- Первое тело покоится.
- Наименьший путь за первые три секунды прошло второе тело.
- Третье тело движется равноускоренно.
- Пятое тело совершает равнопеременное движение.
Решение
Из графика видно, что в момент времени t=0с наибольшей начальной скоростью обладает тело 2.
Третье тело движется равноускоренно, т.к. график скорости напрвлен вверх.
Ответ: 14
Рекомендуемые курсы подготовки
- 14.02.2022
Третья тренировочная работа по физике от составителей работ СтатГрада. Работа составлена и проведена по аналогии с ЕГЭ по демоверсии ЕГЭ 2022 по физике. Включая все изменения 2022 года
Работа проводилась 11 февраля 2022 года для выпускников 11 классов, которые сдают ЕГЭ по физике.
- Другие тренировочные работы по физике
На видео мы разбираем каждое задание этой тренировочной работы, способ решение и правильный ответ.
- Другие работы ЕГЭ Статград 2022 года.
Смотрите, задавайте комментарии ниже, обсуждайте эту работу и ее детальный видеоразбор.
Вариант №1
Вариант №2
Вариант №3
Часть №1 варианта №4
Часть №2 варианта №4
Вариант №5
Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
$p↖{→}=mυ↖{→}$
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$
где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$
Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
$∆p↖{→}=F↖{→}∆t$
Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+…$
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
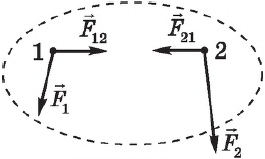
Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$
Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.
Следовательно,
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:
${∆p_{сист}}↖{→}=F↖{→}∆t$
где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:
$m_{p}υ_p=m_{газ}·υ_{газ}$
Отсюда следует, что скорость ракеты
$υ_p=({m_{газ}}/{m_p})·υ_{газ}$
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
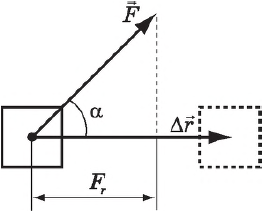
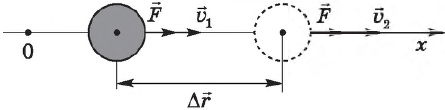
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
$A=F|∆r↖{→}|cosα$
где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.
Работа — величина скалярная. Если $α < 90°$, то $А > 0$, а если $90° < α < 180°$, то $A < 0$; если же $α = 90°$, то $А = 0$. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. Также при движении спутника по круговой орбите сила тяготения не совершает работу.
При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.
Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.
Работа силы тяжести
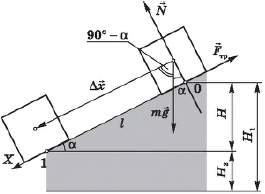
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.
Выразим $∆x$ через $H$ и $α$:
$∆x={H}/{sinα}$
Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° — α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:
$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
- работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
- при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.
Работа силы трения
Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:
$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$
Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то
$A_{тр}=μmgHctgα$
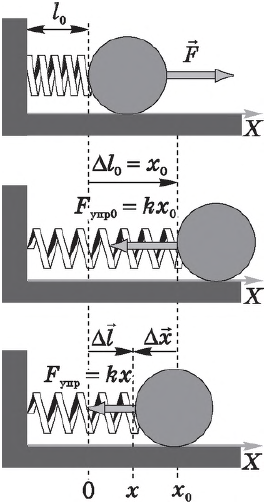
Работа силы упругости
Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:
$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$
Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:
$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$
Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.
Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.
Мощность силы
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).
Мощность определяется формулой:
$N={A}/{∆t}$
где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.
Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:
$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.
Кинетическая энергия. Закон изменения кинетической энергии
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.
Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.
Энергия, которой обладает тело вследствие движения, называется кинетической энергией.
Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.
Найдем кинетическую энергию тела массой $m$, движущегося со скоростью $υ$. Поскольку кинетическая энергия — это энергия, обусловленная движением, нулевым состоянием для нее является то состояние, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем его кинетическую энергию.
Для этого подсчитаем работу на участке перемещения $∆r↖{→}$ при совпадении направлений векторов силы $F↖{→}$ и перемещения $∆r↖{→}$. В этом случае работа равна
$A=F·∆x,$
где $∆x=∆r$
Для движения точки с ускорением $α=const$ выражение для перемещения имеет вид:
$∆x=υ_1t+{at^2}/{2},$
где $υ_1$ — начальная скорость.
Подставив в уравнение $A=F·∆x$ выражение для $∆x$ из $∆x=υ_1t+{at^2}/{2}$ и воспользовавшись вторым законом Ньютона $F=ma$, получим:
$A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$
Выразив ускорение через начальную $υ_1$ и конечную $υ_2$ скорости $a={υ_2-υ_1}/{t}$ и подставив в $A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$ имеем:
$A={m(υ_2-υ_1)}/{2}·(2υ_1+υ_2-υ_1)$
или
$A={mυ_2^2}/{2}-{mυ_1^2}/{2}$
Приравняв теперь начальную скорость к нулю: $υ_1=0$, получим выражение для кинетической энергии:
$E_K={mυ}/{2}={p^2}/{2m}$
Таким образом, движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую необходимо совершить, чтобы увеличить скорость тела от нуля до значения $υ$.
Из $E_K={mυ}/{2}={p^2}/{2m}$ следует, что работа силы по перемещению тела из одного положения в другое равна изменению кинетической энергии:
$A=E_{K_2}-E_{K_1}=∆E_K$
Равенство $A=E_{K_2}-E_{K_1}=∆E_K$ выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за это время силой, действующей на тело.
Потенциальная энергия
Потенциальной энергией называется энергия, определяемая взаимным расположением взаимодействующих тел или частей одного и того же тела.
Поскольку энергия определяется как способность тела совершать работу, то потенциальную энергию, естественно, определяют как работу силы, зависящую только от взаимного расположения тел. Таковой является работа силы тяжести $A=mgh_1-mgh_2=mgH$ и работа силы упругости:
$A={kx_0^2}/{2}-{kx^2}/{2}$
Потенциальной энергией тела, взаимодействующего с Землей, называют величину, равную произведению массы $m$ этого тела на ускорение свободного падения $g$ и на высоту $h$ тела над поверхностью Земли:
$E_p=mgh$
Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости (жесткости) $k$ тела на квадрат деформации $∆l$:
$E_p={1}/{2}k∆l^2$
Работа консервативных сил (тяжести и упругости) с учетом $E_p=mgh$ и $E_p={1}/{2}k∆l^2$ выражается следующим образом:
$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.
Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.
Закон изменения и сохранения механической энергии
Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:
$E=E_k+E_p$
Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).
Согласно теореме о кинетической энергии,
$E_k-E_{k_1}=A_p+A_{пр},$
где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.
В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:
$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$
где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.
Итак, закон изменения механической энергии гласит:
Изменение механической энергии системы равно работе всех непотенциальных сил.
Механическая система, в которой действуют только потенциальные силы, называется консервативной.
В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:
В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):
$E_k+E_p=E_{k_1}+E_{p_1}$
Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).
Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.
Закон сохранения механической энергии является следствием однородности времени.
Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.
Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.
В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.
Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.
В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.
Вот как в современной физике формулируется понятие энергии:
Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
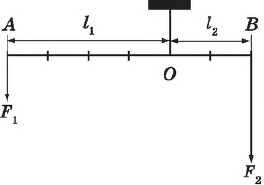
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Неподвижный блок
Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:
$F_1=F_2$
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок
Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:
$F_1={F_2}/{2}$
где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
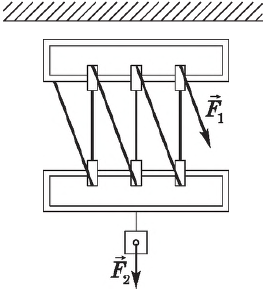
Полиспаст (система блоков)
Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:
$F_1={F_2}/{2n}$
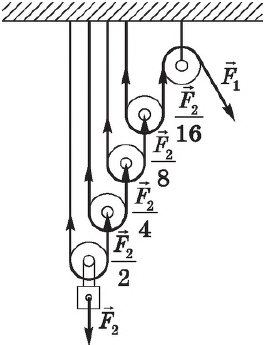
Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:
$F_1={F_2}/{2^n}$
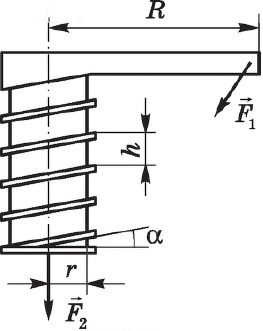
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
Условие равновесия сил, действующих на винт, имеет вид:
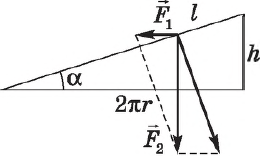
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
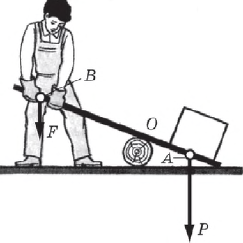
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Столкновение тел. Упругий и неупругий удары
Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.
Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$
Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).
Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.
Для абсолютно упругого удара справедливы уравнения
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ’_1}↖{→}+m_2{υ’_2}↖{→};$
${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ’_1)^2}/{2}+{m_2(υ’_2)^2}/{2}$
где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ’_1, υ’_2$ —скорости шаров после удара.