Решу егэ 10316 - Помощь в подготовке к экзаменам и поступлению

Задание 1 № 10316

В кодировке КОИ-8 каждый символ кодируется 8 битами. Лена написала текст (в нём нет лишних пробелов):

«Ява, Куба, Лусон, Маражо, Суматра, Сулавеси, Эспаньола — острова».

Ученица вычеркнула из списка название одного из островов. Заодно она вычеркнула ставшие лишними запятые и пробелы — два пробела не должны идти подряд.

При этом размер нового предложения в данной кодировке оказался на 9 байтов меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название острова.

2. Задание 2 № 1121

От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе:

• • — • • • — • — — • — • • • • —

При передаче радиограммы было потеряно разбиение на буквы, но известно, что в радиограмме использовались только следующие буквы:

Т	А	У	Ж	Х
—	• —	• • —	• • • —	• • • •

Определите текст радиограммы.

3. Задание 3 № 18424

Напишите наименьшее число X, для которого истинно высказывание:

(X 16) И НЕ (X нечётное).

4. Задание 4 № 18187

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых в (километрах) приведена в таблице.

	A	B	C	D	E	F
A		3	5			15
B	3		1	4
C	5	1		2		9
D		4	2		3	6
E				3		4
F	15		9	6	4

Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт С. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

5. Задание 5 № 16013

У исполнителя Квадратор две команды. которым присвоены номера:

1. возведи в квадрат

2. прибавь 3

Первая из них возводит число на экране во вторую степень, вторая увеличивает его на 3.

Составьте алгоритм получения из числа 1 числа 25, содержащий не более 5 команд. В ответе запишите только номера команд.

(Например, 12221 — это алгоритм:

возведи в квадрат

прибавь 3

возведи в квадрат,

который преобразует число 2 в 169.)

Если таких алгоритмов более одного, то запишите любой из них.

6. Задание 6 № 10465

Ниже приведена программа, записанная на пяти языках программирования.

Бейсик	Python
DIM s, t AS INTEGER INPUT s INPUT t IF s     PRINT ‘YES’ ELSE     PRINT ‘NO’ ENDIF	s = int(input()) t = int(input()) if s     print(«YES») else:     print(«NO»)
Паскаль	Алгоритмический язык
var s, t: integer; begin     readln(s);     readln(t);     if (s         then writeln(‘YES’)         else writeln(‘NO’) end.	алг нач цел s, t ввод s ввод t если s     то вывод «YES»     иначе вывод «NO» все кон
С++
#include using namespace std; int main() {     int s, t;     cin s;     cin t;     if (s         cout     else         cout return 0; }

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(6, 4); (7, 8); (8, 5); (5, 6); (11, 10); (–5, 7); (–2, 2); (4, 5); (8, 6).

Сколько было запусков, при которых программа напечатала «YES»?

7. Задание 7 № 337

Доступ к файлу hello.jpg, находящемуся на сервере home.info, осуществляется по протоколу ftp. Фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

А) info

Б) ://

В) home.

Г) /

Д) hello

Е) ftp

Ж) .jpg

8. Задание 8 № 10480

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер \| Линкор	4700
Крейсер & Линкор	600
Крейсер	2500

Какое количество страниц (в тысячах) будет найдено по запросу Линкор?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

9. Задание 9 № 10251

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город И, проходящих через город В?

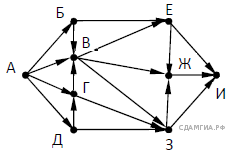
10. Задание 10 № 10331

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

20₁₆, 36₈, 11100₂.

11. Задание 11 № 10536

В одном из произведений А. С. Пушкина, текст которого приведён в подкаталоге Пушкин каталога Проза, присутствует персонаж с именем Владимир. С помощью поисковых средств операционной системы и текстового редактора выясните фамилию этого персонажа.

Выполните задание, распаковав архив на своём компьютере.

DEMO-12.rar

12. Задание 12 № 10510

Сколько файлов с расширением .htm содержится в подкаталогах каталога Проза? В ответе укажите только число.

Выполните задание, распаковав архив на своём компьютере.

DEMO-12.rar

13. Задание 13 № 10589

13.1 Используя информацию и иллюстративный материал, содержащийся в каталоге «Кенгуру», создайте презентацию из трёх слайдов на тему «Кенгуру». В презентации должны содержаться краткие иллюстрированные сведения о внешнем виде, об ареале обитания, образе жизни и рационе кенгуру. Все слайды должны быть выполнены в едином стиле, каждый слайд должен быть озаглавлен.

Кенгуру.rar

13.2 Создайте в текстовом редакторе документ и напишите в нём следующий текст, точно воспроизведя всё оформление текста, имеющееся в образце.

Данный текст должен быть написан шрифтом размером 14 пунктов. Основной текст выровнен по ширине, и первая строка абзаца имеет отступ в 1 см. В тексте есть слова, выделенные жирным шрифтом, курсивом и подчеркиванием.

При этом допустимо, чтобы ширина Вашего текста отличалась от ширины текста в примере, поскольку ширина текста зависит от размера страницы и полей. В этом случае разбиение текста на строки должно соответствовать стандартной ширине абзаца.

14. Задание 14 № 11051

В электронную таблицу занесли данные наблюдения за погодой в течение одного года. Ниже приведены первые пять строк таблицы.

	А	B	C	D	E	F
1	Дата	Температура	Осадки	Давление	Ветер	Скорость ветра
2	1 января	0,7	15,2	748	ЮВ	4,2
3	2 января	0,4	4,6	751	В	4,7
4	3 января	–1,9	1,4	747	C	2,4
5	4 января	–7,7	0,2	752	З	4,7

В столбце A записана дата наблюдения, в столбце B – среднесуточная температура воздуха для указанной даты, в столбце C – количество выпавших осадков (в миллиметрах) для указанной даты, в столбце D – среднесуточное атмосферное давление (в миллиметрах ртутного столба). В столбце E записано направление ветра для указанной даты – одно из восьми возможных значений «СЗ», «С», «СВ», «В», «ЮВ», «Ю», «ЮЗ», «З». В столбце F записана среднесуточная скорость ветра (в метрах в секунду). Всего в электронную таблицу были занесены данные по всем 365 дням года в хронологическом порядке.

Выполните задание.

Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса и постройте диаграмму:

1. Какой была средняя температура воздуха в весенние месяцы (март, апрель, май)? Ответ на этот вопрос запишите в ячейку H2 таблицы с точностью до сотых.

2. Какое среднее количество осадков выпадало за сутки в те дни года, когда дул южный (Ю) ветер? Ответ на этот вопрос запишите в ячейку H3 таблицы с точностью до сотых.

Ответы должны быть вычислены с точностью не менее двух знаков после запятой.

3. Постройте круговую диаграмму, отображающую соотношение направлений ветров «ЮВ», «Ю», «ЮЗ». Левый верхний угол диаграммы разместите вблизи ячейки G6.

task 14.xls

15. Задание 15 № 581

Выберите ОДНО из предложенных ниже заданий: 15.1 или 15.2.

15.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:

вверх вниз влево вправо

При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.

Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:

сверху свободно  снизу свободно  слева свободно  справа свободно

Эти команды можно использовать вместе с условием «если», имеющим следующий вид:

если условие то

последовательность команд

все

Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:

если справа свободно то

вправо

закрасить

все

В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:

если (справа свободно) и (не снизу свободно) то

вправо

все

Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:

нц пока условие

последовательность команд

кц

Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:

нц пока справа свободно

вправо

кц

Выполните задание.

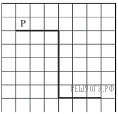
На бесконечном поле имеется стена, длины отрезков стены неизвестны. Стена состоит из 3 последовательных отрезков: вправо, вниз, вправо, все отрезки неизвестной длины. Робот находится в клетке, расположенной над левым концом первого отрезка. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные над первым отрезком и справа от второго. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.

15.2 Напишите программу, которая в последовательности натуральных чисел определяет количество всех чётных чисел, кратных 9. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 — признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число: количество всех чётных чисел, кратных 9.

Пример работы программы:

Входные данные	Выходные данные
27 24 18 22 36 0	2

Источник

Установление соответствия

Задание 10316

Установите соответствие между событиями и годами: к каждой
позиции первого столбца подберите соответствующую позицию из второго столбца.

	СОБЫТИЯ		ГОДЫ
А)	созыв первого Земского собора	1)	1185 г.
Б)	издание манифеста о вольности дворянской	2)	1549 г.
В)	поход новгород-северского князя Игоря Святославича против половцев	3)	1613 г.
Г)	I Съезд народных депутатов СССР	4)	1762 г.
		5)	1918 г.
		6)	1989 г.

Решение:

2416

ЕГЭ
Справочник

youtube

Источник

Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.

Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.

Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.

Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.

Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.

Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.

Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.

Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.

Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.

Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .

Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.

Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?

Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле F_A = ρgl³, где l – длина ребра куба в метрах, ρ = 1000 кг/м³ – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.

Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

Задание 10.
На рисунке изображён график функции f(x) = ax² + bx + c. Найдите значение f(−1).

Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.

Задание 11.
Найдите точку минимума функции y = x³ − 27x²+ 13.

Задание 12.
а) Решите уравнение 2cos³x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]

Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.

Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.

Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Задание 16.
В треугольнике ABC медианы AA₁, BB₁ и CC₁ пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 22.

Задание 17.
Найдите все значения a, при каждом из которых система уравнений

begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 \ 3x-4y=2a+3 end{cases}

не имеет решений.

Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?

Источник варианта: СтатГрад/statgrad.org.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 3

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.admin2023-03-05T19:16:30+03:00

Источник

Физика решу егэ 10316

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 12 № 10316

На PV-диаграмме показан циклический процесс, состоящий из двух изохор и двух адиабат. В качестве рабочего вещества используется одноатомный идеальный газ.

Из приведённого ниже списка выберите все правильные утверждения.

1) Данный цикл соответствует циклу идеальной тепловой машины (циклу Карно).

2) В процессе 4–1 газ получил количество теплоты 450 Дж.

3) В процессе 2–3 газ отдал в 4 раза большее количество теплоты, чем получил в процессе 4–1.

4) Внутренняя энергия газа в процессе 1–2 уменьшается.

5) В процессах 1–2 и 3–4 газ не совершает работы.

Проверим правильность утверждений.

1) Цикл Карно состоит из двух изотерм и двух адиабат. Утверждение 1 — неверно.

2) Согласно первому началу термодинамики, переданное газу тепло идёт на изменение его внутренней энергии и на совершение работы против внешних сил: Процесс 4–1 является изохорный, а значит, работа газа в нём равна нулю. Газ получил

Утверждение 2 — верно.

3) В процессе 2–3 объём газа в 4 раза больше, а вот давление изменяется меньше, чем в процессе 4–1. Утверждение 3 — неверно.

4)По первому закону термодинамики при адиабатном процессе изменение внутренней энергии равно минус работа газа. Газ расширяется, совершая положительную работу, следовательно, в процессе 1–2 внутренняя энергия уменьшилась. Утверждение 4 — верно.

5) Объём газа в процессах 1–2 и 3–4 изменяется, а значит, газом или над газом совершается работа. Утверждение 5 — неверно.

Задание 12 № 10316

—>

Газ получил.

Phys-ege. sdamgia. ru

19.09.2019 13:12:42

2019-09-19 13:12:42

Источники:

Http://phys-ege. sdamgia. ru/problem? id=10316

Тренировочные варианты ЕГЭ 2022 по физике » /> » /> .keyword { color: red; } Физика решу егэ 10316

Тренировочные варианты ЕГЭ 2022 по физике

Подборка тренировочных вариантов ЕГЭ 2022 по физике для 11 класса с ответами из различных источников.

Easy-physic. ru
Вариант 101	Ответы
Вариант 102	Ответы
Вариант 103	Ответы
Вариант 104	Ответы
Вариант 105	Ответы
Вариант 106	Ответы
Вариант 107	Ответы
Вариант 108	Ответы
Вариант 109	Ответы
СтатГрад
Тренировочная работа в формате ЕГЭ 2022	Ответы
ЕГЭ 100 баллов (с ответами)
Вариант 2	Скачать
Вариант 3	Скачать
Вариант 5	Скачать
Вариант 6	Скачать
Вариант 7	Скачать
Вариант 10	Скачать
Вариант 12	Скачать
Вариант 13	Скачать
→ купить сборник тренировочных вариантов ЕГЭ по физике

Структура варианта КИМ ЕГЭ 2022 по физике

Каждый вариант экзаменационной работы состоит из двух частей и включает в себя 30 заданий, различающихся формой и уровнем сложности.

Часть 1 содержит 23 задания с кратким ответом, из них 11 заданий с записью ответа в виде числа или двух чисел и 12 заданий на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр.

Часть 2 содержит 7 заданий с развёрнутым ответом, в которых необходимо представить решение задачи или ответ в виде объяснения с опорой на изученные явления или законы.

При разработке содержания КИМ учитывается необходимость проверки усвоения элементов знаний, представленных в разделе 2 кодификатора.

Продолжительность ЕГЭ по физике

На выполнение всей экзаменационной работы отводится 235 минут. Примерное время на выполнение заданий экзаменационной работы составляет:

− для каждого задания с кратким ответом – 2–5 минут;

− для каждого задания с развёрнутым ответом – от 5 до 20 минут.

Дополнительные материалы и оборудование

Перечень дополнительных устройств и материалов, пользование которыми разрешено на ЕГЭ, утверждён приказом Минпросвещения России и Рособрнадзора. Используется непрограммируемый калькулятор (на каждого участника экзамена) с возможностью вычисления тригонометрических функций (cos, sin, tg) и линейка

Дополнительные материалы и оборудование.

Vpr-ege. ru

27.06.2020 0:09:55

2020-06-27 00:09:55

Источники:

Http://vpr-ege. ru/ege/fizika/1428-trenirovochnye-varianty-ege-2022-po-fizike

Решу егэ физика тесты. Подготовка к ЕГЭ по физике: примеры, решения, объяснения » /> » /> .keyword { color: red; } Физика решу егэ 10316

Решу егэ физика тесты. Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Лебедева Алевтина Сергеевна, учитель физики, стаж работы 27 лет. Почетная грамота Министерства образования Московской области (2013 год), Благодарность Главы Воскресенского муниципального района (2015 год), Грамота Президента Ассоциации учителей математики и физики Московской области (2015 год).

В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т. е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.

На рисунке представлен график зависимости модуля скорости от времени T . Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость V = 10 м/с, т. е.

S =	(30 + 20) С	10 м/с = 250 м.
2

Ответ. 250 м.

Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени T . Определите модуль силы натяжения троса в течение подъема.

Решение. По графику зависимости проекции скорости V груза на ось, направленную вертикально вверх, от времени T , можно определить проекцию ускорения груза

A =	∆V	=	(8 – 2) м/с	= 2 м/с 2 .
∆T	3 с

На груз действуют: сила тяжести, направленная вертикально вниз и сила натяжения троса, направленная вдоль троса вертикально вверх смотри рис. 2. Запишем основное уравнение динамики. Воспользуемся вторым законом Ньютона. Геометрическая сумма сил действующих на тело равна произведению массы тела на сообщаемое ему ускорение.

Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем

T – Mg = Ma (2);

Из формулы (2) модуль силы натяжения

Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.

Ответ . 1200 Н.

Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью модуль которой равен 1, 5 м/с, прикладывая к нему силу так, как показано на рисунке (1). При этом модуль действующей на тело силы трения скольжения равен 16 Н. Чему равна мощность, развиваемая силой F ?

Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.

Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения тр. и сила, с которой тело тащат. Проекция силы трения отрицательная, так как вектор силы не совпадает с направлением оси Х . Проекция силы F положительная. Напоминаем, для нахождения проекции опускаем перпендикуляр из начала и конца вектора на выбранную ось. С учетом этого имеем: F cosα – F тр = 0; (1) выразим проекцию силы F , это F cosα = F тр = 16 Н; (2) тогда мощность, развиваемая силой, будет равна N = F cosα V (3) Сделаем замену, учитывая уравнение (2), и подставим соответствующие данные в уравнение (3):

N = 16 Н · 1,5 м/с = 24 Вт.

Ответ. 24 Вт.

Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения X груза от времени T . Определите, чему равна масса груза. Ответ округлите до целого числа.

Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза Х от времени T , определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π выразим массу M груза.

=	T	;	M	=	T 2	; M = K	T 2	; M = 200 H/м	(4 с) 2	= 81,14 кг ≈ 81 кг.
2π	K	4π 2	4π 2	39,438

Ответ: 81 кг.

На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите Два верных утверждения и укажите в ответе их номера.

Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н. Изображенная на рисунке система блоков не дает выигрыша в силе. H , нужно вытянуть участок веревки длиной 3H . Для того чтобы медленно поднять груз на высоту HH .

Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:

Для того чтобы медленно поднять груз на высоту H , нужно вытянуть участок веревки длиной 2H . Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.

В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?

Увеличивается; Уменьшается; Не изменяется.

Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити F упр, направленная вдоль нити вверх; сила тяжести, направленная вертикально вниз; архимедова сила A , действующая со стороны жидкости на погруженное тело и направленная вверх. По условию задачи масса грузов одинакова, следовательно, модуль действующей на груз силы тяжести не меняется. Так как плотность грузов разная, то объем тоже будет разный

Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж Разбираем задания ЕГЭ по физике (Вариант С) с учителем.

S =	(30 + 20) С	10 м/с = 250 м.
2

Ответ. 250 м.

A =	∆V	=	(8 – 2) м/с	= 2 м/с 2 .
∆T	3 с

T – Mg = Ma (2);

Из формулы (2) модуль силы натяжения

Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.

Ответ . 1200 Н.

N = 16 Н · 1,5 м/с = 24 Вт.

Ответ. 24 Вт.

=	T	;	M	=	T 2	; M = K	T 2	; M = 200 H/м	(4 с) 2	= 81,14 кг ≈ 81 кг.
2π	K	4π 2	4π 2	39,438

Ответ: 81 кг.

Увеличивается; Уменьшается; Не изменяется.

Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН ПО ФИЗИКЕ ДЛИТСЯ 235 мин

2) СТРУКТУРА КИМов — 2018 и 2019 по сравнению с 2017г. несколько ИЗМЕНИЛАСЬ: Вариант экзаменационной работы будет состоять из двух частей и включит в себя 32 задания. Часть 1 будет содержать 24 задания с кратким ответом, в том числе задания с самостоятельной записью ответа в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр. Часть 2 будет содержать 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (25–27) и 5 заданий (28–32), для которых необходимо привести развернутый ответ. В работу будут включены задания трех уровней сложности. Задания базового уровня включены в часть 1 работы (18 заданий, из которых 13 заданий с записью ответа в виде числа, двух чисел или слова и 5 заданий на соответствие и множественный выбор). Задания повышенного уровня распределены между частями 1 и 2 экзаменационной работы: 5 заданий с кратким ответом в части 1, 3 задания с кратким ответом и 1 задание с развернутым ответом в части 2. Последние четыре задачи части 2 являются заданиями высокого уровня сложности. Часть 1 экзаменационной работы будет включать два блока заданий: первый проверяет освоение понятийного аппарата школьного курса физики, а второй – овладение методологическими умениями. Первый блок включает 21 задание, которые группируются, исходя из тематической принадлежности: 7 заданий по механике, 5 заданий по МКТ и термодинамике, 6 заданий по электродинамике и 3 по квантовой физике.

Новым заданием базового уровня сложности является последнее задание первой части (24 позиция), приуроченное к возвращению курса астрономии в школьную программу. Задание имеет характеристику типа «выбор 2 суждений из 5». Задание 24, как и другие аналогичные задания в экзаменационной работе, оценивается максимально в 2 балла, если верно указаны оба элемента ответа, и в 1 балл, если в одном из элементов допущена ошибка. Порядок записи цифр в ответе значения не имеет. Как правило, задания будут иметь контекстный характер, т. е. часть данных, необходимых для выполнения задания будут приводиться в виде таблицы, схемы или графика.

В соответствии с этим заданием в кодификаторе добавился подраздел «Элементы астрофизики» раздела «Квантовая физика и элементы астрофизики», включающий следующие пункты:

· Солнечная система: планеты земной группы и планеты-гиганты, малые тела Солнечной системы.

· Звёзды: разнообразие звездных характеристик и их закономерности. Источники энергии звезд.

· Современные представления о происхождении и эволюции Солнца и звёзд. Наша галактика. Другие галактики. Пространственные масштабы наблюдаемой Вселенной.

· Современные взгляды на строение и эволюцию Вселенной.

Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М. Ю. Демидовой https://www. youtube. com/watch? v=JXeB6OzLokU либо в документе, приведенном ниже.

Изменений в заданиях ЕГЭ по физике на 2019 Год нет.

Структура заданий ЕГЭ по физике-2019

Экзаменационная работа состоит из двух частей, включающих в себя 32 задания .

Часть 1 содержит 27 заданий.

В заданиях 1–4, 8–10, 14, 15, 20, 25–27 ответом является целое число или конечная десятичная дробь. Ответом к заданиям 5–7, 11, 12, 16–18, 21, 23 и 24 является последовательность двух цифр. Ответом к заданиям 19 и 22 являются два числа.

Часть 2 содержит 5 заданий. Ответ к заданиям 28–32 включает в себя подробное описание всего хода выполнения задания. Вторая часть заданий (с развёрнутым ответом) оцениваются экспертной комиссией на основе.

Темы ЕГЭ по физике, которые будут в экзаменационной работе

Механика (кинематика, динамика, статика, законы сохранения в механике, механические колебания и волны). Молекулярная физика (молекулярно-кинетическая теория, термодинамика). Электродинамика и основы СТО (электрическое поле, постоянный ток, магнитное поле, электромагнитная индукция, электромагнитные колебания и волны, оптика, основы СТО). Квантовая физика и элементы астрофизики (корпускулярноволновой дуализм, физика атома, физика атомного ядра, элементы астрофизики).

Продолжительность ЕГЭ по физике

На выполнение всей экзаменационной работы отводится 235 минут .

Примерное время на выполнение заданий различных частей работы составляет:

для каждого задания с кратким ответом – 3–5 минут; для каждого задания с развернутым ответом – 15–20 минут.

Что можно брать на экзамен:

Используется непрограммируемый калькулятор (на каждого ученика) с возможностью вычисления тригонометрических функций (cos, sin, tg) и линейка. Перечень дополнительных устройств и, использование которых разрешено на ЕГЭ, утверждается Рособрнадзором.

Важно. не стоит рассчитывать на шпаргалки, подсказки и использование технических средств (телефонов, планшетов) на экзамене. Видеонаблюдение на ЕГЭ-2019 усилят дополнительными камерами.

Баллы ЕГЭ по физике

1 балл — за 1-4, 8, 9, 10, 13, 14, 15, 19, 20, 22, 23, 25, 26, 27 задания. 2 балла — 5, 6, 7, 11, 12, 16, 17, 18, 21, 24. З балла — 28, 29, 30, 31, 32.

Всего: 52 баллов (максимальный первичный балл).

Что необходимо знать при подготовки заданий в ЕГЭ:

Знать/понимать смысл физических понятий, величин, законов, принципов, постулатов. Уметь описывать и объяснять физические явления и свойства тел (включая космические объекты), результаты экспериментов… приводить примеры практического использования физических знаний Отличать гипотезы от научной теории, делать выводы на основе эксперимента и т. д. Уметь применять полученные знания при решении физических задач. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

С чего начать подготовку к ЕГЭ по физике:

Изучать теорию, необходимую для каждого заданий. Тренироваться в тестовых заданиях по физике, разработанные на основе ЕГЭ. На нашем сайте задания и варианты по физике будут пополняться. Правильно распределяй время.

Желаем успеха!

ЕГЭ по физике – экзамен, который не входит в перечень испытаний обязательных для сдачи всеми выпускниками. Физику выбирают потенциальные студенты инженерных специальностей. Причем, каждый ВУЗ устанавливает свою планку – в престижных учебных заведениях она может быть очень высокой. Это должен понимать выпускник, начиная подготовку к экзамену. Цель экзамена – проверка уровня знаний и умений, полученных в ходе школьного обучения, на соответствие нормам и стандартам, указанным в программе.

На экзамен отводится практически 4 часа – 235 минут, это время необходимо правильно распределить между заданиями, чтобы успешно справиться со всеми, не теряя ни одной минуты. Разрешается брать с собой калькулятор, поскольку для выполнения заданий требуется множество сложных расчетов. Также можно взять линейку. Работа состоит из трех частей, каждая имеет свои особенности, состоит из заданий разного уровня сложности.

Физика относится к сложным предметам, приблизительно каждый 15-1 сдает этот экзамен ежегодно, чтобы поступить в технический ВУЗ. Предполагается, что выпускник с такими целями не будет учить предмет «с нуля», чтобы подготовиться к ЕГЭ.
Чтобы удачно пройти испытание, необходимо:

Всего 52 баллов максимальный первичный балл.

Liardi. ru

25.02.2019 13:35:55

2019-02-25 13:35:55

Источники:

Http://liardi. ru/sprains/reshu-ege-fizika-testy-podgotovka-k-ege-po-fizike-primery-resheniya. html

Источник