Найдите наибольшее значение функции на отрезке
Спрятать решение
Решение.
Найдем производную заданной функции:
Уравнение не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 5.
Задания
Версия для печати и копирования в MS Word
Задания Д18 № 132367
Найдите наибольшее значение функции на отрезке
Спрятать решение
Решение.
Найдем производную заданной функции:
Уравнение не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 5.
Аналоги к заданию № 77497: 132367 132319 132321 132323 132325 132327 132329 132331 132333 132335 … Все
Спрятать решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-21

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Натуральное вещественное
число 132367
.
Произведение и сумма цифр числа: 756, 22.
У числа 2 делителя: 1, 132367.
132368 — сумма делителей.
132367 и 0.000007554753072895813 — это обратные числа.
Это число можно представить произведением: 1 * 132367.
Перевод числа 132367 в другие системы счисления:
двоичная система: 100000010100001111, троичная: 20201120111, восьмеричная: 402417, шестнадцатеричная: 2050F.
Число 132367 в байтах это 129 килобайтов 271 байт .
В виде кода азбуки Морзе: .—- …— ..— …— -…. —…
Число — не число Фибоначчи.
Синус 132367: -0.7610, косинус 132367: 0.6487, тангенс 132367: -1.1731.
Натуральный логарифм равен 11.7933.
Логарифм десятичный числа: 5.1218.
363.8228 — квадратный корень из числа 132367, 50.9636 — корень кубический.
Возведение числа в квадрат: 1.7521e+10.
Перевод из числа секунд — 1 день 12 часов 46 минут 7 секунд .
В нумерологии число 132367 означает цифру 4.
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2023 с ответами и критериями оценивания.
Изменений относительно 2022 года нет, потому актуальны и варианты прошлого года.
Тренировочные варианты ОГЭ 2023 по математике
| alexlarin.net | уровень 1 | уровень 2 |
| вариант 327 | larin22-oge-327-1 | larin22-oge-327 |
| вариант 328 | larin22-oge-328-1 | larin22-oge-328 |
| вариант 329 | larin23-oge-329-1 | larin23-oge-329 |
| вариант 330 | larin23-oge-330-1 | larin23-oge-330 |
| вариант 331 | larin23-oge-331-1 | larin23-oge-331 |
| вариант 332 | larin23-oge-332-1 | larin23-oge-332 |
| вариант 333 | larin23-oge-333-1 | larin23-oge-333 |
| вариант 334 | larin23-oge-334-1 | larin23-oge-334 |
| вариант 335 | larin23-oge-335-1 | larin23-oge-335 |
| вариант 336 | larin23-oge-336-1 | larin23-oge-336 |
| вариант 337 | larin23-oge-337-1 | larin23-oge-337 |
| вариант 338 | larin23-oge-338-1 | larin23-oge-338 |
| вариант 339 | larin23-oge-339-1 | larin23-oge-339 |
| вариант 340 | larin23-oge-340-1 | larin23-oge-340 |
| вариант 341 | larin23-oge-341-1 | larin23-oge-341 |
| вариант 342 | larin23-oge-342-1 | larin23-oge-342 |
| вариант 343 | larin23-oge-343-1 | larin23-oge-343 |
| вариант 344 | larin23-oge-344-1 | larin23-oge-344 |
| вариант 345 | larin23-oge-345-1 | larin23-oge-345 |
| вариант 346 | larin23-oge-346-1 | larin23-oge-346 |
| вариант 347 | larin23-oge-347-1 | larin23-oge-347 |
| вариант 348 | larin23-oge-348-1 | larin23-oge-348 |
| вариант 349 | larin23-oge-349-1 | larin23-oge-349 |
| вариант 350 | larin23-oge-350-1 | larin23-oge-350 |
| вариант 351 | larin23-oge-351-1 | larin23-oge-351 |
| вариант 352 | larin23-oge-352-1 | larin23-oge-352 |
| math100.ru | |
| Вариант 54 | math100-oge-54 |
| Вариант 55 | math100-oge-55 |
| Вариант 56 | math100-oge-56 |
| Вариант 57 | math100-oge-57 |
| Вариант 58 | math100-oge-58 |
| Вариант 59 | math100-oge-59 |
| Вариант 60 | math100-oge-60 |
| Вариант 61 | math100-oge-61 |
| Вариант 62 | math100-oge-62 |
| Вариант 63 | math100-oge-63 |
| Вариант 64 | math100-oge-64 |
| Вариант 65 | math100-oge-65 |
| Вариант 66 | math100-oge-66 |
| Вариант 67 | math100-oge-67 |
| Вариант 68 | math100-oge-68 |
| Вариант 69 | math100-oge-69 |
| Вариант 70 | math100-oge-70 |
| Вариант 71 | math100-oge-71 |
| Вариант 72 | math100-oge-72 |
| Вариант 73 | math100-oge-73 |
| Вариант 74 | math100-oge-74 |
| Вариант 75 | math100-oge-75 |
| Вариант 76 | math100-oge-76 |
| Вариант 77 | math100-oge-77 |
| Вариант 78 | math100-oge-78 |
| Вариант 79 | math100-oge-79 |
| Вариант 80 | math100-oge-80 |
| time4math.ru | |
| Варианты 1-2 | ответы |
| Варианты 3-4 | ответы |
| Варианты 5-6 | ответы |
| Варианты 7-8 | ответы |
| Варианты 9-10 | ответы |
| Варианты 11-12 | ответы |
| Варианты 13-14 | ответы |
| Варианты 15-16 | ответы |
| vk.com/pezhirovschool | |
| Вариант 1 (с решением) | скачать |
| Вариант 2 (с решением) | скачать |
| Вариант 3 (с решением) | скачать |
| Вариант 4 (с решением) | скачать |
| Вариант 5 (с ответами) | скачать |
| Вариант 6 | скачать |
| vk.com/oge100ballov | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| variant 4 | скачать |
| yagubov.ru | |
| вариант 33 (сентябрь) | скачать |
| вариант 34 (октябрь) | скачать |
| вариант 35 (ноябрь) | скачать |
| вариант 36 (декабрь) | скачать |
| вариант 37 (январь) | скачать |
| вариант 38 (февраль) | скачать |
| вариант 39 (март) | скачать |
| vk.com/math.studying | |
| вариант 1 | ответы |
| вариант 2 | ответы |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
Характеристика структуры и содержания КИМ ОГЭ 2023 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом. При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики.
Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Связанные страницы:
Задание 1
В треугольнике $$ABC$$ известно, что $$AC=BC$$, высота $$AH$$ равна $$6sqrt{6}$$, $$BH=3$$ Найдите $$cos BAC$$.
Ответ: 0,2
Скрыть
Задание 2
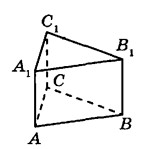
Найдите объём многогранника, вершинами которого являются точки $$B$$, $$C$$, $$A_1$$, $$C_1$$ правильной треугольной призмы $$ABCA_1B_1C_1$$ площадь основания которой равна 5, а боковое ребро равно 6.
Ответ: 10
Скрыть
Задание 3
В группе туристов 25 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист 3. полетит третьим рейсом вертолёта.
Ответ: 0,2
Скрыть
Номер рейса в этой задаче не имеет значения. Важно, что за один рейс перевозятся 5 человек. То есть, вероятность попасть туристу З. на какой-либо рейс (в том числе и 3-й), равна:
$$P=frac{m}{n}=frac{5}{25}=frac{1}{5}=0,2$$
Задание 4
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 5. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,56
Скрыть
Задание 5
Найдите корень уравнения $$(frac{1}{4})^{x+2}=256^{x}$$
Ответ: -0,4
Скрыть
Задание 6
Найдите значение выражения $$log_{2,5}6cdot log_{6} 0,4$$
Ответ: -1
Скрыть
Задание 7
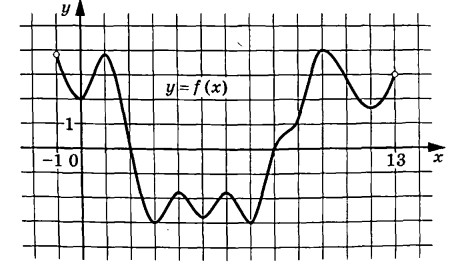
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-1; 13)$$. Найдите количество точек, в которых касательная к графику функции $$y=f(x)$$ параллельна прямой $$y=-2$$.
Ответ: 9
Скрыть
Задание 8
Высота над землёй подброшенного вверх мяча меняется по закону $$y=1,4+11t-5t^2$$, где $$h$$ — высота в метрах, $$t$$ — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 0,6
Скрыть
Задание 9
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси? Сколько секунд мяч будет находиться на высоте не менее 7 метров?
Ответ: 55
Скрыть
Задание 10
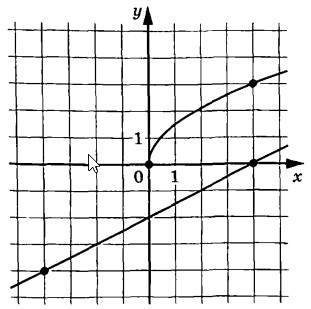
На рисунке изображены графики функций $$f(x)=asqrt{x}$$ и $$g(x)=kx+b$$, которые пересекаются в точке $$A(x_0; y_0)$$. Найдите $$y_0$$.
Ответ: 6
Скрыть
Задание 11
Найдите точку максимума функции промежутку $$y=(2x-1)cos x-2sin x+9$$, принадлежащую промежутку $$(0;frac{pi}{2})$$
Ответ: 0,5
Скрыть
Задание 12
а) Решите уравнение $$log^{2}_{2}(4x^{2})+3log_{0,5}(8x)=1$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[0,15;1,5]$$
Ответ: а)$$0,25;sqrt[4]{8}$$ б)$$0,25$$
Скрыть
Задание 13
Сторона основания правильной четырёхугольной пирамиды $$SABCD$$ относится к боковому ребру как $$1:sqrt{2}$$. Через вершину $$D$$ проведена плоскость $$alpha$$, перпендикулярная боковому ребру $$SB$$ и пересекающая его в точке $$M$$.
а) Докажите, что $$M$$ — середина $$SB$$.
б) Найдите расстояние между прямыми $$AC$$ и $$DM$$, если высота пирамиды равна $$6sqrt{3}$$.
Ответ: 3
Скрыть
Задание 14
Решите неравенство $$frac{sqrt{x+4}(8-3^{2+x^{2}})}{4^{x-1}-3}leq 0$$
Ответ: $$-4;(log_{4}12;+infty)$$
Скрыть
Задание 15
15 июня 2025 года Сергей Данилович планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
— в январе каждого года действия кредита долг увеличивается на 15 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
— в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.
Ответ: 8 млн. руб.
Скрыть
Задание 16
Окружность с центром в точке $$C$$ касается гипотенузы $$AB$$ прямоугольного треугольника $$ABC$$ и пересекает его катеты $$AC$$ и $$BC$$ в точках $$E$$ и $$F$$. Точка $$D$$ — основание высоты, опущенной из вершины $$C$$. $$I$$ и $$J$$ — центры окружностей, вписанных в треугольники $$BCD$$ и $$ACD$$.
а) Докажите, что $$I$$ и $$J$$ лежат на отрезке $$EF$$.
б) Найдите расстояние от точки $$C$$ до прямой $$IJ$$, если $$AC=15$$, $$BC = 20$$.
Ответ: $$6sqrt{2}$$
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых оба уравнения $$a+frac{x}{2}=|x|$$ и $$asqrt{2}+x=sqrt{2asqrt{2}-x^{2}+12}$$ имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.
Ответ: $$[sqrt{2};frac{3sqrt{6}}{sqrt{13}})$$
Скрыть
Задание 18
Трёхзначное число, меньшее 910, поделили на сумму его цифр и получили натуральное число $$n$$.
а) Может ли $$n$$ равняться 68?
б) Может ли $$n$$ равняться 86?
в) Какое наибольшее значение может принимать $$n$$, если все цифры ненулевые?
Ответ: а)да б)нет в)79
Скрыть