Задания
Версия для печати и копирования в MS Word
Тип 14 № 13600
Сколько единиц содержится в двоичной записи значения выражения: 4255 + 2255 − 255?
Спрятать решение
Решение.
Преобразуем выражение: 4255 + 2255 − 255 = 2510 + 2255 − 28 + 1.
Двоичная запись числа 2k — 2m это k — m единиц и m нулей
Поэтому у 2510 + 2255 − 28 + 1 есть 1 + 1 +(255-8) = 249 единиц.
Ответ: 249.
Приведём другое решение на языке Python.
x = 4**255 + 2**255 — 255
s = »
while x != 0:
s += str(x % 2)
x //= 2
s = s[::-1]
print(s.count(«1»))
Раздел кодификатора ФИПИ: 1.4.1 Позиционные системы счисления
Спрятать решение
·
·
Сообщить об ошибке · Помощь
Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
Видеокурс — это то, с чего лучше всего начать подготовку к ЕГЭ по информатике.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Задание 11
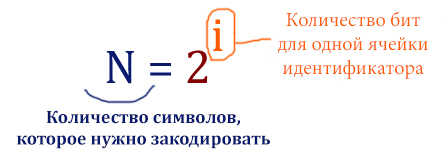
При регистрации в компьютерной системе каждому объекту присваивается
идентификатор, состоящий из 250 символов и содержащий только
десятичные цифры и символы из 1650-символьного специального алфавита.
В базе данных для хранения каждого идентификатора отведено одинаковое
и минимально возможное целое число байт. При этом используется
посимвольное кодирование идентификаторов, все символы кодируются
одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536
идентификаторов. В ответе запишите только целое число – количество
Кбайт.
Решение:
Воспользуемся формулой для 11-ого задания из ЕГЭ по информатике.
Вместо N подставляем число 1650 + 10 = 1660 (1650 символов плюс 10 цифр). Тогда
1660 < 211
Т.е. 11 бит точно хватит, чтобы закодировать 1650 символов.
В идетификаторе всего 250 ячейки. Найдём сколько будет «весить» один идетификатор: 250 * 11 = 2750 бит. Узнаем, сколько байт потребуется для одного идентификатора 2772 / 8 = 344 байт (округлили в большую сторону, чтобы точно хватило).
У нас всего 65536 идентификаторов. Тогда нам потребуется 65536 * 344 = 22544384 байт. Переведём в Кб: 22544384 / 1024 = 22016 Кб.
Ответ: 22016
Задание 12
Исполнитель Редактор получает на вход строку цифр и преобразовывает её.
Редактор может выполнять две команды, в обеих командах v и w обозначают
цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на
цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя
Редактор. Если она встречается, то команда возвращает логическое значение
«истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие
ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся
с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2»,
расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений
цифр строки, получившейся в результате выполнения программы, является
простым числом.
Решение:
Есть отличный разбор 12 задания в видеокурсе по подготовке к ЕГЭ по информатике.
Единица превращается в две двойки. Двойка преходим в саму себя. Ноль превращается в 1.
Изначально было 39 нулей. Значит, 39 единиц уже точно будет в строке, после выполнения программы. Так же там будет 39 двоек. Т.е., если не брать во внимание n единиц, сумма в результате будет 39 + 39 * 2 = 117.
Нужно прибавить некоторое количество чевёрок, чтобы получилось ближайшее простое число.
117 + 4*5 = 137.
Получается 5 единиц.
Ответ: 5
Задание 13
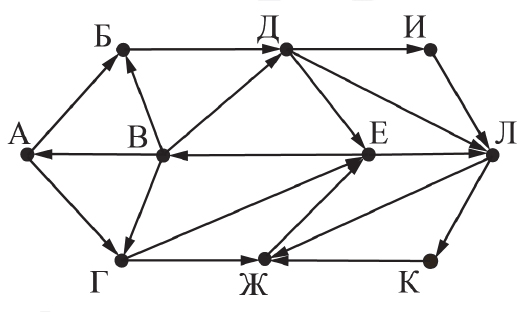
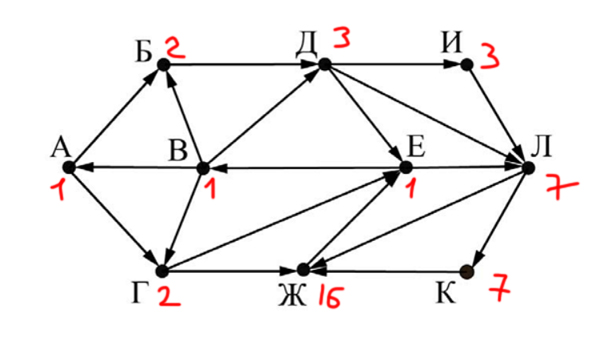
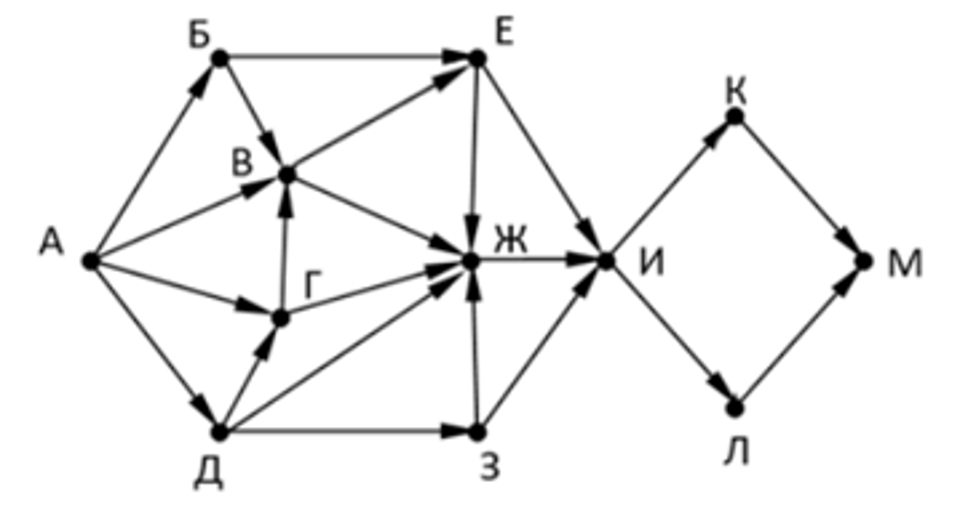
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении,
указанном стрелкой.
Определите количество различных путей ненулевой длины, которые
начинаются и заканчиваются в городе Е, не содержат этот город в качестве
промежуточного пункта и проходят через промежуточные города не более
одного раза.
Решение:
Решать будем примерно так же, как и классическую задачу. Основные идеи ни чем не отличаются.
В город Е входят города с числами: 16, 2 и 3. Значит, ответ получается 16 + 2 + 3 = 21.
Ответ: 21
Задание 14
Операнды арифметического выражения записаны в системе счисления
с основанием 15.
123×515 + 1×23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита
15-ричной системы счисления. Определите наименьшее значение x, при
котором значение данного арифметического выражения кратно 14. Для
найденного значения x вычислите частное от деления значения
арифметического выражения на 14 и укажите его в ответе в десятичной
системе счисления. Основание системы счисления в ответе указывать
не нужно.
Решение:
Решим с помощью программирования на языке Python.
for x in '0123456789ABCDE': r = int('123' + x + '5', 15) + int('1' + x + '233', 15) if r%14==0: print(r//14) break
Перебираем для переменной x все цифры в пятнадцатиричной системе. Вычисляем значение выражение. Функция int может перевести строку, записанную в пятнадцатиричной системе, в число.
Остаётся только найти нужное значение и остановить цикл с помощью break.
Ответ: 8767
Задание 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A >= 100)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x ?
Решение:
Применим шаблон из видокурса ЕГЭ по информатике.
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 10000): if (not(D(x, 2)) or not(D(x, 3))) or (x + A >= 100): k=k+1 if k==9999: print(A)
Здесь в начале пишем функцию D, которая олицетворяет функцию ДЕЛ. Потом перебираем различные натуральные значения A. Если функция для какого-то значения сработает 9999 раз, то будем считать, что такое значение A нам подходит.
Самое маленькое значение получается 74.
Ответ: 94
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
В решении к заданию 11 вы пишите: «У нас всего 4096 идетификаторов». Пожалуй, надо исправить на «65 536 идентификаторов»…
1
Задание 1. Однозначное соотнесение графа и таблицы
Между населёнными пунктами П1, П2, П3, П4, П5, П6, П7 построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами П1 и П7, проходящего через пункт П6, минуя пункт П2 (при условии, что передвигаться можно только по построенным дорогам).
2
Задание 2. Заполнение таблицы истинности
Логическая функция F задается выражением ((x→w) ≡ (y→z)) / ¬ (w≡y) / ¬ (k→z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F,содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w, k.
| ? | ? | ? | ? | F | |
| 1 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 |
В ответе напишите буквы x, y, z, w, k в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3
Задание 3. Фильтры и таблицы
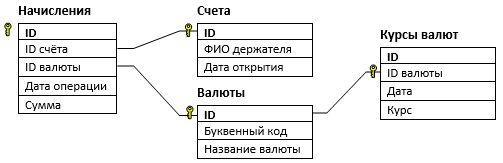
В файле 3-dv.xls приведён фрагмент базы данных «Инвестиционные счета». Таблица «Счета» содержит информацию о владельце счёта и дате его открытия. Таблица «Валюты» содержит информацию о наименованиях валют, которые могут храниться на счетах. Таблица «Курс валют» содержит информацию о курсах валют по отношению к рублю курс валют за период с 24 по 30 декабря 2021 года. Таблица «Начисления» содержит информацию о всех операциях со счетом: код счёта, код валюты, дату операции и сумму начисления (она может быть отрицательной). На рисунке приведена схема указанной базы данных.
Даня и Ваня решили подзаработать, чтобы купить курсы по информатике в лучшей школе 99 баллов. Для этого они хотят найти валюту, которая больше всего прибавила в цене в период с 24 по 30 декабря. Используя информацию из приведённой базы данных, определите буквенное обозначение валюты, которая больше всего прибавила в цене с 24 по 30 декабря. В ответе укажите только 3 заглавные буквы.
4
Задание 4. Минимальная длина кода
По каналу связи передаются сообщения, содержащие девять букв: Х, Д, Б, Р, А, С, Ю, Е, З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Х — 011, Б-000, Р-111, Ю — 010, З — 001, Е — 110. Какое наименьшее количество символов потребуется, чтобы закодировать сообщение ХАРДБАСС?
5
Задание 5. Двоичные алгоритмы
Автомат получает на вход натуральное число N и строит по нему новое число R по следующему алгоритму:
1) Исходное число переводится в двоичную систему счисления
2) Подсчитывается количество значащих 0. Если их кол-во чётно — из числа убирается последняя цифра, иначе справа дописывается ‘1’.
3) Второй шаг повторяется еще один раз
4) Результат переводится в десятичную систему счисления.
Укажите сколько получится различных R, которые можно получить при исходном N на отрезке [200, 300].
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a,b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x+a, y+b). Если числа a, b положительные, то значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2,-3) переместит Чертёжника в точку (6,-1). Запись
Повтори k раз
Команда1 Команда2 Команда3
конец
означает, что последовательность Команда1 Команда2 Команда3 повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 10 раз
Сместиться на (4, 6)
Сместиться на (-4, 6)
Сместиться на (-4, -6)
Сместиться на (4, -6)
конец
Найдите площадь полученной фигуры.
7
Задание 7. Кодирование изображений
Danny Golds делает фотоснимки размером 1920×2550 пикселей. На хранение одного кадра отводится 15600 Кбайт. Определите максимальную глубину цвета (в битах на пиксель), которую можно использовать при фотосъёмке.
8
Задание 8. Составление комбинаций
Вероника составляет 13-буквенные слова из букв М, А, Й, К, О, В, выбирая такие, в которых содержится комбинация МАЙКОВА. Сколько слов сможет составить Вероника?
Откройте файл электронной таблицы 9-107.xls, содержащий в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов прямоугольного треугольника, выраженных в градусах. В ответе запишите только число.
С помощью текстового редактора определите, сколько различных чисел встречается в тексте рассказа Валентина Распутина «Уроки французского» (10-d1.docx). Одинаковые числа повторно не считать. В ответе укажите только количество чисел.
11
Задание 11. Пароли с дополнительной информацией
Датчик считывает значения интенсивности поступающего света, которые округляются до одного из 2000 возможных. Каждое считанное значение кодируется одинаковым минимально возможным количеством бит. Известно, что значения считываются сериями по 50 измерений, все серии сохраняются в одном файле. Каждая серия занимает целое количество байт. Если последняя серия содержит меньше 50 значений, она сохраняется в файле с помощью минимально возможного целого количества байт. За время своей работы датчик считал 12312 значений. Какое минимальное целое количество килобайт нужно выделить для хранения файла?
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 223>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 11>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 30 цифр 1, 20 цифр 2 и 10 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
13
Задание 13. Поиск числа путей
Ваня спешит на пересдачу из общежития (Пункт А) в Иннополис (Пункт М). Чтобы он смог выбрать самый оптимальный маршрут и успеть вовремя, ему нужно знать все возможные варианты добраться до ВУЗа. На рисунке представлена схема дорог, связывающих здания А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из общежития до Иннополиса и не проходящих через военкомат (Пункт В)?
14
Задание 14. Системы счисления (прямое сложение)
Сколько различных цифр в шестнадцатеричной записи числа 2^51 + 2^45 + 2^30 + 4^7 – 2^5
15
Задание 15. Поразрядная коъюнкция
Определите количество натуральных чисел A из интервала [80, 300] таких, что выражение
((X & 55 ≠ 0) (X & 23 ≠ 0)) → (X & A ≠ 0)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?
16
Задание 16. Рекурсивные алгоритмы
Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:
F(0) = 1
F(n) = F(n–1) + F(n–2), при чётном n > 0
F(n) = 1,5*F(n–1), при нечётном n > 0
Сколько различных цифр встречается в целой части значения функции F(35)?
17
Задание 17. Числовая последовательность
В файле 17-d5.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 1000. Определите сначала количество пар, в которых оба элемента больше, чем сумма всех цифр «3» в шестеричной записи всех чисел в файле, кратных 15, а затем максимальную из сумм таких пар. Под парой подразумевается два идущих подряд элемента последовательности.
18
Задание 18. Двумерное динамическое программирование
Квадрат разлинован на N×N клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трёх команд: вправо, вверх или вправо-вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю, а по команде вправо-вверх – на одну клетку вправо и вверх по диагонали. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записана величина вознаграждения от 1 до 100. Попав в клетку после хода вправо или вверх, Робот получает указанное в ней вознаграждение, а если он попал в клетку после выполнения команды вправо-вверх, вознаграждение удваивается. Это также относится к начальной и конечной клетке маршрута Робота. Определите максимальное и минимальное вознаграждение, которое может получить Робот, пройдя из левой нижней клетки в правую верхнюю. В ответе укажите два числа без пробелов – сначала максимальное вознаграждение, затем минимальное. Исходные данные записаны в файле 18-5.xls в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата.
19
Задание 19. Теория игр (Задания 19)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20
Задание 20. Теория игр (Задания 20)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21
Задание 21. Теория игр (Задания 21)
13. Теория игр. Две кучи Excel
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 40. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 40 или больше камней. В начальный момент в первой куче было 9 камней, во второй куче – S камней, 1 ≤ S ≤ 30. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
13. Сколько существует значений S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22
Задание 22. Параллельные процессы
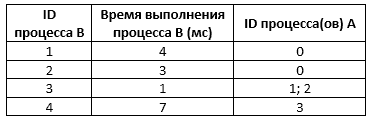
В файле 22d-3 содержится информация о вычислительных процессов проектов P1 и P2, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Найдите время завершения процессов 5 из проектов P1 и P2. В ответ укажите их сумму.
Типовой пример организации данных в файле:
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23
Задание 23. Одномерное динамическое программирование
Исполнитель Шахматный Король преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавь 2
2. Прибавь 3
3. Умножь на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 20 и при этом не содержат двух команд умножения подряд?
24
Задание 24. строковая обработка
Текстовый файл 24-d12.txt содержит заглавные латинские буквы и телефонные номера, всего не более чем 106 символов. Телефонный номер – это последовательность цифр, расположенных между буквами. В некоторой стране Z номер телефона состоит из 11 цифр, начинается на 8 и при этом его вторая слева цифра равна предпоследней. Определите количество телефонных номеров страны Z, содержащихся в файле.
25
Задание 25. Поиск делителей
Найдите наименьшее натуральное число, которое имеет ровно 1024 делителя. В ответе запишите сначала само число и затем его наибольший простой делитель. Подсказка: используйте основную теорему арифметики.
26
Задание 26. Сортировки
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 640 на 480 точек. При попадании очередной частицы на экран в файл записываются координаты чувствительного элемента: номер строки (целое число от 1 до 640) и номер позиции в строке (целое число от 1 до 480). Точка экрана, в которую попала хотя бы одна частица, считается светлой, точка, в которую ни одна частица не попала, – тёмной.
Вам нужно определить наибольшую длину цепочки в одной строке, состоящей только из светлых точек, и строку, в котором она находится. Если таких строк несколько, укажите максимальный из их номеров.
Входные данные представлены в файле 26-73.txt следующим образом. В первой строке входного файла записано целое число N – количество частиц, попавших на экран. В каждой из следующих N строк записаны по два числа, разделённые пробелом: номер строки и номер позиции в строке.
Запишите в ответе два числа: сначала наибольшую длину цепочки из светлых точек, затем – номер строки, в которой находится эта цепочка (если таких строк несколько, запишите максимальный из их номеров).
Пример входного файла:
7
1 2
2 3
3 6
2 4
1 3
2 5
2 4
При таких исходных данных имеется три цепочки светлых точек: в позициях 2 и 3 строки 1, в позициях 4, 5 и 6 строки 2 (это самая длинная цепочка!) и точка в позиции 6 строки 3. Ответ: 3 2.
27
Задание 27. Кратность произведения пары
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов не кратно 10 и 7.
Отличная работа!
Так держать!
Если остались вопросы, напиши своему куратору.
Нужно авторизоваться
Нужно авторизоваться
Введите больше 6 символов
На почту 12345@mail.ru отправлена ссылка для сброса пароля.
Пожалуйста, подтвердите ваш номер телефона
Курс заблокирован
К сожалению, данный курс заблокирован. Необходимо внести доплату
Вывод
средств
Ваше задание
подтверждено!
успешно
Теперь вы можете приступить
к следующему уроку
курса по математике
Перейти к уроку
Подтверждение
замены
Для смены номера телефона
мы отправили Вам код по СМС,
введите его в поле ниже.
Подтвердить
Ты включаешь автопродление — 25-го числа каждого месяца доступ к купленным курсам будет автоматически продлеваться. Деньги будут списываться с одной из привязанных к учетной записи банковских карт. Управлять автопродлением можно из раздела «Финансы»
Для активации регулярного платежа мы спишем небольшую сумму с карты и сразу её вернем
Вы дествительно хотите отменить автопродление?
Благодарим за покупку!
В ближайшее время курс будет доступен в разделе Моё обучение
Материалы будут доступны за сутки до начала урока
Чат будет доступен после выдачи домашнего задания
Укажите вашу электронную почту
Вариант заданий с реального ЕГЭ 2022 по информатике 11 класс, которые попались 20 и 21 июня на экзамене. Вариант составлен для ознакомления по заданиям, которые были (либо были похожие) на экзамене по информатике.
Скачать вариант ЕГЭ 2022 по информатике
Скачать файлы к варианту
Вариант с реального ЕГЭ 2022 по информатике 11 класс
егэ2022_информатика_реальный_вариант
Видео решения варианта
1)На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта A в пункт D и из пункта G в пункт C. В ответе запишите целое число.
Ответ: 66
2)Миша заполнял таблицу истинности логической функции F ¬(w → z) / (x → y) / ¬x, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Ответ: wzyx
3)Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид. Используя информацию из приведённой базы данных, определите, на сколько увеличилось количество упаковок всех видов макарон производителя «Макаронная фабрика», имеющихся в наличии в магазинах Первомайского района, за период с 1 по 8 июня включительно.
Ответ: 1610
4)По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Ответ: 14
5)На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1. Строится двоичная запись числа N. 2. Далее эта запись обрабатывается по следующему правилу: а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10; б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11. Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее, чем 16. В ответе запишите это число в десятичной системе счисления.
Ответ: 8
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 8. Для Вашего удобства программа представлена на четырёх языках программирования.
Ответ: 81
7)Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кбайт памяти без учёта размера заголовка файла. Файл оригинального изображения больше сжатого на 35%. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Ответ: 2048
8)Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.
Ответ: 2961
9)Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: – наибольшее из четырёх чисел меньше суммы трёх других; – четыре числа можно разбить на две пары чисел с равными суммами. В ответе запишите только число.
Ответ: 391
10)Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «солдаты» со строчной буквы. Другие формы этого слова учитывать не следует. В ответе запишите только число.
Ответ: 26
11)При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Ответ: 1388
12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить(v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить(111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить(v, w) не меняет эту строку. Б) нашлось(v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Ответ: 299
13)На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Ответ: 21
14)Значение арифметического выражения 4 · 6251920 + 4 · 1251930 – 4 · 251940 – 3 · 51950 – 1960 записали в системе счисления с основанием 5. Определите количество значащих нулей в записи этого числа.
Ответ: 1891
15)Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) / (x + A ≥ 80) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
Ответ: 74
16)Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n < 3; F(n) = F(n − 1) + n − 1, если n > 2 и при этом n чётно; F(n) = F(n − 2) + 2 × n − 2, если n > 2 и при этом n нечётно. Чему равно значение функции F(34)?
Ответ: 574
17)В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых остаток от деления хотя бы одного из элементов на 117 равен минимальному элементу последовательности. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
18)Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 259. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 259 или больше камней. В начальный момент в первой куче было 17 камней, во второй куче – S камней; 1 ≤ S ≤ 241. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20)Для игры, описанной в предыдущем задании, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: − Петя не может выиграть за один ход; − Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 8, а потом 21.
23)Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Вычти 1 2. Найди целую часть от деления на 2 Первая из них уменьшает число на экране на 1, вторая заменяет число на экране на целую часть от деления числа на 2. Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 30 результатом является число 1, и при этом траектория вычислений содержит число 12? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 122 при исходном числе 10 траектория состоит из чисел 9, 4, 2.
24)Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполнения этого задания следует написать программу.
25)Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: – символ «?» означает ровно одну произвольную цифру; – символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность. Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 108 , найдите все числа, соответствующие маске 1234*7, делящиеся на 141 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 141. Количество строк в таблице для ответа избыточно.
26)В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
27)У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Посмотрите:
- Новая шкала перевода баллов ЕГЭ 2022 по всем предметам
- Тренировочные варианты ЕГЭ 2022 по информатике
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тип 1 № 14218
i
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 | |
| П1 | 37 | 23 | ||||||
| П2 | 25 | 44 | 46 | |||||
| П3 | 25 | |||||||
| П4 | 37 | 34 | 42 | |||||
| П5 | 34 | 24 | 28 | |||||
| П6 | 44 | 24 | 29 | |||||
| П7 | 42 | 28 | 29 | 31 | ||||
| П8 | 23 | 46 | 31 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Г. В ответе запишите целое число.
ВНИМАНИЕ. Длины отрезков на схеме не отражают длины дорог.
Ответ:
2
Тип 2 № 35976
i
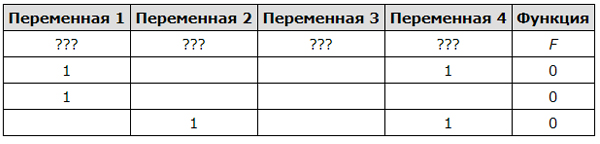
Логическая функция F задаётся выражением ((x ∧ ¬y) ≡ (z ∨ ¬w)) → (x ∧ z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | ||
| 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Ответ:
3
Тип 3 № 37489
i
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите, сколько литров молока безлактозного было продано в магазинах Октябрьского района за период с 1 по 10 июня включительно.
В ответе запишите только число.
Ответ:
4
Тип 4 № 39233
i
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: М — 11, Л — 10, У — 001. Какое наименьшее количество двоичных знаков может содержать код слова МОЛОКО?
Ответ:
5
Тип 5 № 26949
i
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается справа два нуля, если число четное, или две единицы в противном случае
Укажите максимальное число N, после обработки которого с помощью этого алгоритма получается число менее 94. В ответе это число запишите в десятичной системе.
Ответ:
6
Тип 6 № 47314
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 7 Направо 90 Вперёд 4 Направо 90]
Определите количество точек с целочисленными координатами, лежащих внутри или на границе области, которую ограничивает заданная алгоритмом линия.
Ответ:
7
Тип 7 № 16384
i
Автоматическая фотокамера производит растровые изображения размером 512 на 300 пикселей. При этом объём файла с изображением не может превышать 150 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?
Ответ:
8
Тип 8 № 13540
i
Пётр составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Пётр использует все пятибуквенные слова в алфавите {A, B, C, D, E, F}, удовлетворяющие такому условию: кодовое слово не может начинаться с буквы F и заканчиваться буквой A. Сколько различных кодовых слов может использовать Пётр?
Ответ:
9
Тип 9 № 45243
i
Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел.
9.xlsx
Определите количество строк таблицы, в которых квадрат суммы максимального и минимального чисел в строке больше суммы квадратов трёх оставшихся.
Ответ:
10
Тип 10 № 33512
i
Определите, сколько раз в тексте произведения Н. В. Гоголя «Нос» встречается слово «полный» в любом числе и падеже.
Задание 10
Ответ:
11
Тип 11 № 4970
i
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы Е, Г, Э, 2, 0, 1, 3. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объем памяти, отводимый этой программой для записи 25 паролей. (Ответ дайте в байтах.)
Ответ:
12
Тип 12 № 26957
i
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно).
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>3)
ТО заменить (>3, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 26 цифр 1, 10 цифр 2 и 14 цифр 3, расположенных в произвольном порядке.
Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
Ответ:
13
Тип 13 № 18591
i
На рисунке — схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П.
Сколько существует различных путей из пункта А в пункт П, проходящих через пункт Е?
Ответ:
14
Тип 14 № 48391
Операнды арифметического выражения записаны в системах счисления с основаниями 12 и 14:
yAAx12 + x02y14
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 80. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 80 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Ответ:
15
Тип 15 № 33485
i
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
ДЕЛ(120, A) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 18) → ¬ДЕЛ(x, 24)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Ответ:
16
Тип 16 № 6306
i
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = n при n ≤ 2;
F(n) = F(n − 1) × F(n − 2) при n> 2.
Чему равно значение функции F(7)? В ответе запишите только натуральное число.
Ответ:
17
Тип 17 № 37370
i
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых разность элементов кратна 60 и хотя бы один из элементов кратен 15, затем максимальную из разностей элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.
17.txt
Ответ:
18
Тип 18 № 27666
i
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
Ответ:
19
Тип 19 № 47016
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите наименьшее значение S, при котором Петя не может выиграть за один ход, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом.
Ответ:
20
Тип 20 № 47017
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
В ответе запишите найденные значения в порядке возрастания: сначала меньшее, затем большее.
Ответ:
21
Тип 21 № 47018
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Найдите наибольшее значение S, при котором у Пети есть выигрышная стратегия, позволяющая ему выиграть третьим ходом при любой игре Вани, но у Пети нет стратегии, которая позволяла бы ему гарантированно выиграть первым или вторым ходом.
Ответ:
22
Тип 22 № 47601
В файле 22_20.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
Ответ:
23
Тип 23 № 27307
i
Исполнитель РазДва преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя РазДва — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 62, и при этом траектория вычислений содержит число 14 и не содержит числа 59?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 4 траектория будет состоять из чисел 8, 9, 18.
Ответ:
24
Тип 24 № 33494
i
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы E.
Например, в тексте EBCEEBEDDD после буквы E два раза стоит B, по одному разу — E и D. Для этого текста ответом будет B.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
Ответ:
25
Тип 25 № 36880
i
Найдите все натуральные числа N, принадлежащие отрезку [400 000 000; 600 000 000], которые можно представить в виде N = 2m · 3n, где m — чётное число, n — нечётное число. В ответе запишите все найденные числа в порядке возрастания.
Ответ:
26
Тип 26 № 45260
i
В лесничестве саженцы сосны высадили параллельными рядами, которые пронумерованы идущими подряд натуральными числами. Растения в каждом ряду пронумерованы натуральными числами начиная с единицы.
По данным аэрофотосъёмки известно, в каких рядах и на каких местах растения не прижились. Найдите ряд с наибольшим номером, в котором есть ровно 13 идущих подряд свободных мест для посадки новых сосен, таких, что непосредственно слева и справа от них в том же ряду растут сосны. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: наибольший номер ряда и наименьший номер места для посадки из числа найденных в этом ряду подходящих последовательностей из 13 свободных мест.
Входные данные.
26.txt
В первой строке входного файла находится число N — количество прижившихся саженцев сосны (натуральное число, не превышающее 20 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 100 000: номер ряда и номер места в этом ряду, на котором растёт деревце.
Выходные данные
Два целых неотрицательных числа: наибольший номер ряда и наименьший номер места в выбранной последовательности из 13 мест, подходящих для посадки новых сосен.
Типовой пример организации входных данных
7
40 3
40 7
60 33
50 125
50 129
50 68
50 72
Для приведённого примера, при условии, что необходимо 3 свободных места, ответом является пара чисел: 50; 69.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Ответ:
27
Тип 27 № 37162
i
На вход программы поступает последовательность из целых положительных чисел. Необходимо выбрать такую подпоследовательность подряд идущих чисел, чтобы их сумма была максимальной и делилась на 89, а также её длину. Если таких подпоследовательностей несколько, выбрать такую, у которой длина меньше.
Входные данные.
Файл A
Файл B
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 68000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10000. Программа должна вывести длину найденной последовательности.
Пример входного файла:
8
2
3
4
93
42
34
5
95
Для делителя 50 при указанных входных данных значением искомой суммы должно быть число 100 (3 + 4 + 93 или 5 + 95). Следовательно, ответ на задачу — 2. В ответе укажите два числа: сначала значение искомой длины для файла A, затем для файла B.
Ответ:
Просмотр содержимого документа
«ЕГЭ 2023 Март Информатика Вариант 13»
Подборка вариантов ЕГЭ 2022 по информатике для 11 класса с ответами.
| vk.com/info_ege_academiaa | ||
| вариант 1 | ответы | доп. файлы |
| вариант 2 | ответы | доп. файлы |
| вариант 3 | ответы | доп. файлы |
| вариант 4 | ответы | доп. файлы |
| вариант 5 | ответы | доп. файлы |
| вариант 6 | ответы | доп. файлы |
| вариант 7 | ответы | доп. файлы |
| вариант 8 | ответы | доп. файлы |
| вариант 9 | ответы | доп. файлы |
| вариант 10 | ответы | доп. файлы |
| вариант 11 | ответы | доп. файлы |
| вариант 12 от 11.03.22 | ответы | доп. файлы |
| vk.com/inform_web | ||
| вариант 1 | разбор | файлы |
| вариант 2 | разбор | |
| vk.com/ege100ballov | ||
| Вариант 1 | доп. файлы |
Инструкция по выполнению работы
Экзаменационная работа состоит из 27 заданий с кратким ответом, выполняемых с помощью компьютера.
На выполнение экзаменационной работы по информатике отводится 3 часа 55 минут (235 минут).
Экзаменационная работа выполняется с помощью специализированного программного обеспечения, предназначенного для проведения экзамена в компьютерной форме.
При выполнении заданий Вам будут доступны на протяжении всего экзамена текстовый редактор, редактор электронных таблиц, системы программирования.
Расположение указанного программного обеспечения на компьютере и каталог для создания электронных файлов при выполнении заданий Вам укажет организатор в аудитории.
На протяжении сдачи экзамена доступ к сети Интернет запрещён.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Связанные страницы:
Задание 11 ЕГЭ по информатике
Задание №5 ЕГЭ по информатике — практика
Открытый вариант ЕГЭ по информатике 2021 от ФИПИ
Задание №2 ЕГЭ по информатике — практика
Разбор задания № 17 ЕГЭ по информатике — проверка делимости чисел
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
- () — операции в скобках
- ¬ — логическое отрицание
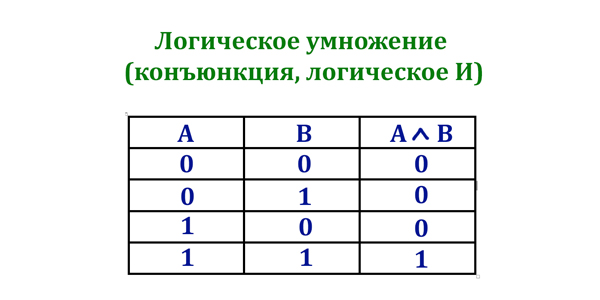
- ∧ — логическое умножение
- ∨ — логическое сложение
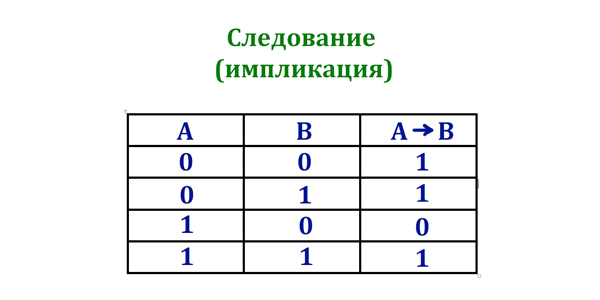
- ⟶ — следование
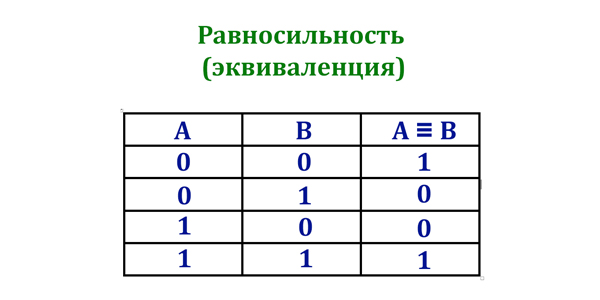
- ≡ — равнозначность
Ещё соотношения:
Передём к решению задач из ЕГЭ по информатике
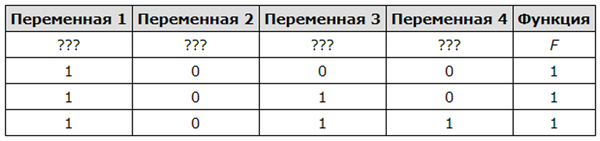
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Задача 2 (средний уровень)
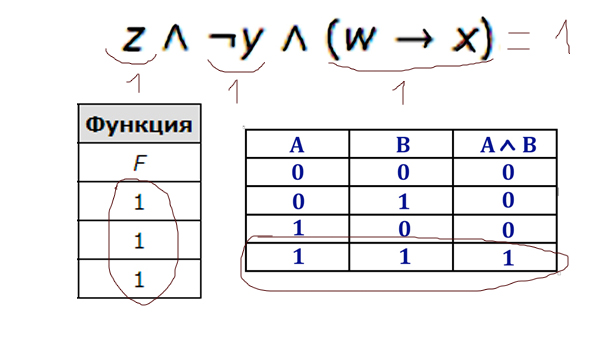
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2 4 ).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Строки с пропущенными значениями 2 задание егэ информатика как решать
Тип 2 № 14688
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| . | . | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ∨ y) → (z ≡ x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной x, и в первом столбце первой строки стоит 1.
Второй столбец таблицы может соответствовать только переменной z, поскольку переменная y принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной y.
Тип 2 № 15097
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет единицы, значит, переменная x находится в третьем столбце. Тогда первая строка имеет вид 0 0 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Второй вариант не удовлетворяет системе (*), а первый удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ z ) ∨ (x → (y ∧ z)) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, третий столбец — это переменная x. Вторая строка соответствует набору (1, 1, 0), в котором единичное значение принимает также переменная y, следовательно, первый столбец — это переменная у, тогда второй столбец — это переменная z.
Тип 2 № 15124
Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет нуля, значит, переменная x находится в первом столбце. Тогда первая строка имеет вид 0 1 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 0 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ y ) ∨ ((y ∨ z) → x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы: (0, 1, 0), (0, 1, 1).
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
В обоих наборах переменная x принимает значение 0, значит, ей может соответствовать только первый столбец таблицы. Переменная z принимает значение 1 только в одном наборе, значит, ей может соответствовать только второй столбец таблицы, тогда третий столбец соответствует переменной у.
Тип 2 № 15618
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 |
|---|---|---|---|
| . | . | . | . |
| 0 | |||
| 1 | 0 | 0 | |
| 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Рассмотрим данное выражение. Преобразуем логическое выражение (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w и получим систему, при которой оно ложно:
Cразу видно, что первый столбец это w, поскольку w всегда должна равняться единице. Также, ясно, что x это переменная 4, так как . Из первого выражения x ∧ ¬y и последней строчке таблицы видно, что переменная 3 это y, а вторая переменная это z.
Рассмотрим, как будет выглядеть полная таблица истинности. Переменная w всегда должна принимать значение 1, поэтому в первом столбце во всех строках будет стоять единица. Исходя из условия можно заключить, что во втором столбце в последней строке будет стоять единица, и в первых двух строках третьего столбца тоже будут стоять единицы. В первой четвёртого столбца должна стоять единица, поскольку строки в таблице истинности должны быть разными.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 |
|---|---|---|---|
| . | . | . | . |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Вариант wyzx не подходит, поскольку в первой строке функция F окажется истинной.
Приведем другое решение.
Составим таблицу истинности функции F и выпишем наборы переменных, при которых функция ложна. Для удобства обозначим эти наборы буквами:
А: (х=0, y=0, z=1, w=1)
Б: (х=0, y=1, z=0, w=1)
В: (х=1, y=1, z=0, w=1)
Заметим, что переменная w всегда должна быть равна 1, поэтому ей соответствует первый столбец заданной таблицы.
Заметим, что вторая и третья строки заданной таблицы, содержащие по два нуля, соответствуют наборам переменных А или Б, тогда первая строка соответствует набору В. Значит, в первой строке z=0, а все остальные переменные равны 1, и переменной z соответствует второй столбец заданной таблицы.
Тогда вторая строка заданной таблицы, в которой переменная z также равна 0, соответствует набору Б, в котором х=0, а остальные переменные равны 1, поэтому переменной х соответствует четвертый столбец таблицы.
Строки с пропущенными значениями 2 задание егэ информатика как решать
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | Функция |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
Логическая функция F задается выражением
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (y ≡ z) ∨ w,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| ? | ? | ? | ? | (¬x∧¬y)∨(y≡z)∨w |
|---|---|---|---|---|
| 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Логическая функция F задается выражением
¬(z ∨ (y ∧ ¬x))
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Видеоразбор
Логическая функция F задается выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.