Решение.
Найдем производную заданной функции: Уравнение
не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 32.
К источнику тока с ЭДС 4 В и внутренним сопротивлением подсоединили нагрузочное сопротивление. Чему оно должно быть равно, чтобы КПД источника был равен 50%? (Ответ дайте в омах.)
Спрятать решение
Решение.
КПД источника определяется как отношение полезной работы (тепла, выделяющегося на нагрузке) к работе, совершаемой ЭДС: Обе эти работы пропорциональны времени, в течение которого пропускается ток, поэтому отношение работ заменим на отношение соответствующих мощностей:
По закону Ома для полной цепи, сила тока в цепи будет равна
Мощность источника равна тогда
напряжение, приходящееся на нагрузку, по закону Ома для участка цепи, равно
Следовательно, полезная мощность:
Таким образом, для того, чтобы КПД был равен 50% необходимо, чтобы выполнялось равенство
Ответ: 5.
Решение.
Найдем производную заданной функции: Уравнение
не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 32.
Незнайка → ОГЭ → География → Вариант 14 → Задание 13
Задание № 23107
Исток реки Волга находится на высоте 300 м, а устье — (—28 м). Длина реки составляет 3531 км. Определите уклон реки. Ответ округлите до сотовых и запишите в виде числа.
Ответ: ____
Решать другие задания по теме: Решение практических задач на основе базового географического материала
Показать ответ
Комментарий:
(300 — -(28) / 3531 = 328 / 3531 = 0,09
Ответ: 0,09
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Задание 1
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Скрыть
Задание 2
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Скрыть
Задание 3
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Скрыть
Задание 4
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Ответ: 0,89
Скрыть
Задание 5
Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$
Ответ: -0,2
Скрыть
Задание 6
Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$
Ответ: 0,5
Скрыть
Задание 7
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.
Ответ: 5
Скрыть
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.
Ответ: 5,832
Скрыть
Задание 9
Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Скрыть
Задание 10
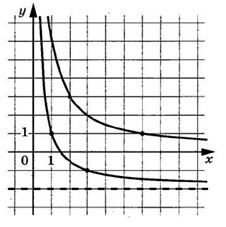
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$
Ответ: -2910
Скрыть
Задание 12
а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$
Скрыть
Задание 13
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.
б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.
Ответ: 24
Скрыть
Задание 14
Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$
Ответ: $$(-infty;1];[log_{4} 28;2,5)$$
Скрыть
Задание 15
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— платежи в 2028 и 2029 годах должны быть равными;
— к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
Ответ: 400 тыс. руб.
Скрыть
Задание 16
В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.
а) Докажите, что $$AL:AC=AB:BC$$.
б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.
Ответ: 14,2
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.
Ответ: (-4;-3);(-3;-1);(-1;0)
Скрыть
Задание 18
Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Ответ: а)да б)нет в)195
Скрыть