Задания
Версия для печати и копирования в MS Word
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Спрятать решение
Решение.
а) Преобразуем уравнение:
Значит, либо откуда
либо
откуда
б) Отберем с помощью единичной окружности корни уравнения, принадлежащие заданному промежутку. Получим числа:
Ответ: а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 507595
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Аналоги к заданию № 507595: 500917 501709 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 12 № 510018
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 12 № 504543
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 504543: 504564 507292 510671 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 12 № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 500366: 500587 501482 514505 Все
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
4 комментария · Сообщить об ошибке · Помощь
5
Тип 12 № 509579
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Аналоги к заданию № 509579: 509926 509947 509968 515762 519665 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Skip to content
ЕГЭ Профиль №12. Тригонометрические уравнения
ЕГЭ Профиль №12. Тригонометрические уравненияadmin2022-08-08T15:32:31+03:00
Используйте LaTeX для набора формулы
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
Тригонометрические уравнения и преобразования
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | $<π>/<6>$ | $<π>/<4>$ | $<π>/<3>$ | $<π>/<2>$ | $π$ |
| $sinα$ | $ 0$ | $ <1>/<2>$ | $ <√2>/<2>$ | $ <√3>/<2>$ | $ 1$ | $ 0$ |
| $cosα$ | $ 1$ | $ <√3>/<2>$ | $ <√2>/<2>$ | $ <1>/<2>$ | $ 0$ | $ -1$ |
| $tgα$ | $ 0$ | $ <√3>/<3>$ | $ 1$ | $ √3$ | $ -$ | $ 0$ |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ <√3>/<3>$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ ($<π>/<2>$ и $<3π>/<2>$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα=/$
- $ctgα=/$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = <5>/ <13>; t ∈(<3π>/<2>;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(<3π>/<2>;2π)$ -это четвертая четверть, то синус в ней имеет знак минус
источники:
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
http://examer.ru/ege_po_matematike/teoriya/trigonometricheskie_vyrageniya
урок 5. Математика ЕГЭ
Тригонометрические уравнения
Тригонометрия – одна из самых важных тем на ЕГЭ по профильной математике. Она может встретиться в №1 (простейшие уравнения), №4 (преобразование выражений, в том числе тригонометрических), знание свойств тригонометрических функций может пригодится в №9, №11 (производные) и в задании из второй части №12 (тригонометрические уравнения).
Как видите, потенциально хорошие знания по тригонометрии могут принести вам до 6 первичных баллов на ЕГЭ. Конечно, вряд ли тригонометрия будет сразу во всех перечисленных номерах, но без нее написать хорошо профильную математику будет сложно.
Самой сложной темой из тригонометрии являются тригонометрические уравнения. Здесь вам понадобятся все ваши умения по работе с тригонометрической окружностью, знание тригонометрических формул, умение работать с тригонометрическими выражениями и переводить градусы в радианы и наоборот. Тригонометрические уравнения почти всегда попадаются в 12-м номере ЕГЭ, а это уже вторая часть, и за это задание дают целых два первичных балла.
Что такое тригонометрические уравнения?
Итак, если в уравнении переменная (x) (или какое-то выражение от (x)) содержится внутри функций синуса, косинуса, тангенса или котангенса, то такое уравнение называется тригонометрическим. Например:
$$3sin(2x)-2cos(x)^2=0;$$
Но будьте внимательными, если уравнения имеет вид:
$$cos(x)+2x=3;$$
То такое уравнение уже будет называться смешанным, так как в нем есть и тригонометрическая функция ((cos(x))), и линейная ((2x)). Такое уравнение уже значительно сложнее, и в ЕГЭ они если и встречаются, то очень редко. Здесь смешанные уравнения мы рассматривать не будем.
Но начинать изучение мы будем с простейших тригонометрических уравнений. Это фундамент, на котором строится все остальное. Простейшие уравнения имеют такой вид:
$$sin(f(x))=a;$$
$$cos(f(x))=a;$$
$$tg(f(x))=a;$$
$$ctg(f(x))=a;$$
где (a) — некоторое число, а (f(x)) – некоторое выражение, зависящее от (x);
Примеры простейших тригонометрических уравнений:
$$sin(x)=frac{1}{2};$$
$$cos(3x)=-1;$$
Как решать тригонометрические уравнения?
Существует два основных метода решения:
- При помощи единичной окружности;
- С использованием готовых формул;
Лично я сторонник решения при помощи единичной окружности. С использованием формул решать, на мой взгляд, не очень удобно, потому что нужно их учить и теряется, как и при любой зубрежке, элемент понимания того, что ты делаешь. Но мы разберем оба способа.
Решение тригонометрического уравнения с синусом на окружности
Здесь необходимо идеальное знание тригонометрической окружности. Если его нет (а без нее в тригонометрии, в любом случае, делать нечего), то рекомендую почитать про нее по ссылке, либо же переходите сразу к методу решения через формулы.
Будем учиться на примере простейшего тригонометрического уравнения:
Пример 1
$$sin(x)=frac{1}{2};$$
Что такое решить уравнение? Значит найти такие значения углов (x), синус от которых будет равен (frac{1}{2}).
Чтобы найти эти самые углы, нарисуем тригонометрическую окружность. (Рис.1)
Рис.1. Тригонометрические уравнения с синусом
На оси синусов (вертикальная ось) отметим значение (frac{1}{2}), обозначим эту точку за (K).
Для того, чтобы понять, какие углы соответствуют этому значению, необходимо провести перпендикуляр (прямая (a)) к оси синусов через точку (K).
Этот перпендикуляр пересечет нашу единичную окружность в двух точках (M) и (N).
Эти точки как раз и будут соответствовать углам, синус от которых будет равен (frac{1}{2}).
На рисунке 1 эти углы отмечены как (angle{MOA}) и (angle{NOA}).
Понятное дело, что мы с вами не можем точно понять по рисунку, что это за углы. Для этого нам понадобится очень точный рисунок на миллиметровке. В нашем случае рисунок показывает нам, что оказывается, есть как минимум два угла (angle{MOA}) и (angle{NOA}), синус от которых будет (frac{1}{2}).
А чтобы найти эти самые углы, мы воспользуемся таблицей значений тригонометрических функций. Видим, что синус равен (frac{1}{2}) от угла в (30^o) или, если в радианах,(frac{pi}{6}).
Рис.2. Таблица значений тригонометрических функций
Но в таблице дан только один угол, синус от которого (frac{1}{2}). И этот угол, если вспомнить, что все положительные углы на единичной окружности отсчитываются от отрезка (OA) против часовой стрелки, судя по всему, соответствует углу (angle{MOA}).
$$x_{1}=frac{pi}{6};$$
А где же взять значение второго угла (angle{NOA})?
И тут нам опять поможет единичная окружность. Посмотрите на рисунок 1: он абсолютно симметричен относительно оси синусов, его можно сложить, как открытку, и правая часть окружности полностью совпадет с левой. Это значит, что углы (angle{MOA}) и (angle{KOC}) равны геометрически:
$$angle{MOA}=angle{KOC}=30^o=frac{pi}{6};$$
Этот интуитивный факт можно строго доказать из равенства треугольников (triangle{MKO}) и (triangle{NKO}).
Итак, из равенства (angle{MOA}=angle{KOC}) можно легко найти угол (angle{NOA}):
$$angle{NOA}=180-angle{KOC}=180-30=150^o;$$
Или в радианах:
$$angle{NOA}=pi-angle{KOC}=pi-frac{pi}{6}=frac{6pi-pi}{6}=frac{5pi}{6};$$
Мы нашли значения обоих углов. Получается, что теперь можем записать значения искомого в уравнении (x):
$$x_{1}=30^o=frac{pi}{6};$$
$$x_{2}=150^o=frac{5pi}{6};$$
Но, к сожалению, ответ пока записывать рано. Потому что есть еще один очень важный момент!
Если вы внимательно изучали предыдущие темы по тригонометрии, то должны знать, что если прибавить к углам (angle{MOA}) и (angle{NOA}) полный оборот ((360^p) или (2pi)), то мы получим новые углы равные соответственно (30^o+360^o=390^o) и (150^o+360^o=510^o), значение синуса которых тоже будет (frac{1}{2})! Так как эти углы тоже соответствуют точкам (M) и (N).
Кроме того, я могу прибавить не один оборот, а хоть миллион оборотов, и опять попаду в те же самые точки (M) и (N), соответствующие синусу (frac{1}{2}). А углы еще бывают отрицательные, и еще можно вычитать полные обороты и опять попадать в эти точки.
Другими словами, у функции синуса есть период, равный ((360^o=2pi)), то есть каждый полный оборот значение синуса будет повторяться.
Для нас это все означает, что существует БЕСКОНЕЧНОЕ количество углов, синус от которых будет (frac{1}{2}) c периодом (360^o=2pi)).
И вот теперь мы можем записать ответ. Он записывается в виде правила, которое описывает это бесконечное количество решений нашего уравнения (правил у нас будет два, каждое соответствует точкам (M) и (N)). И запишу я ответ в радианах, так как в градусах его никто не пишет:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Обратите внимание, что к нашим первоначальным корням (x_{1}=30^o=frac{pi}{6}) и (x_{2}=150^o=frac{5pi}{6}) теперь прибавляется слагаемое (2pi*n), где (n) — это некоторое целое число. Подставляя вместо (n) различные целые числа, вы будете получать углы, удовлетворяющие нашему уравнению. Например, при (n=3) получим корни:
$$x_{1}=frac{pi}{6}+2pi*3=frac{pi}{6}+6pi=frac{37pi}{6};$$
$$x_{2}=frac{5pi}{6}+2pi*3=frac{5pi}{6}+6pi=frac{41pi}{6};$$
А при (n=-2) корни:
$$x_{1}=frac{pi}{6}+2pi*(-2)=frac{pi}{6}-4pi=-frac{23pi}{6};$$
$$x_{2}=frac{5pi}{6}+2pi*(-2)=frac{5pi}{6}-4pi=-frac{19pi}{6};$$
И так можно подставлять абсолютно любые (n) и получать корни.
Таким образом, тригонометрические уравнения обычно имеют бесконечное количество решений, которые записываются в виде некоторых правил, как в нашем примере. Запомните это, почему-то немногие это понимают.
Ответ:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z.$$
Пример 2
$$sin(x)=-frac{sqrt{2}}{2};$$
Этот пример так подробно, как предыдущий, разбирать не будем, а только распишем алгоритм решения:
- Рисуем тригонометрическую окружность;
- Отмечаем примерное значение (-frac{sqrt{2}}{2}approx-frac{1,4}{2}=-0,7) на оси синусов в точке (P);
- Проводим перпендикуляр к оси синусов через точку (P);
- Получили две точки пересечения с единичной окружностью (F) и (T);
- Согласно построению, углы (angle{AOF}) и (angle{AOT}) искомые (показаны на рис. 3 синим цветом): синус от них будет равен (-frac{sqrt{2}}{2}). Не забываем отсчитывать углы от отрезка (OA) ПРОТИВ часовой стрелки, здесь углы будут тупыми, как показано на рисунке;
- Выяснили при помощи окружности, что нас устраивает как минимум два значения (x) (угол (angle{AOF}) и (angle{AOT}));
- Внимание! Осталось найти значения этих углов. И вот тут у нас загвоздка, так как значение синуса у нас отрицательное, и его нет в таблице стандартных углов. Как же найти углы?
Но зато в таблице есть значение (frac{sqrt{2}}{2})! (См.Рис. 2)
Проделаем и отметим на окружности все предыдущие шаги, как будто мы решаем уравнение (sin(x)=frac{sqrt{2}}{2}). Теперь все происходит в верхней половине окружности. Обозначим углы, синус от которых (frac{sqrt{2}}{2}) за (angle{MOA}) и (angle{NOA}). Эти углы мы найти можем, так как значение синуса (frac{sqrt{2}}{2}) есть в таблице стандартных углов:
$$angle{MOA}=45^o=frac{pi}{4};$$
Аналогично примеру №1 находим:
$$angle{NOA}=180^o-angle{NOC}=180^o-45^o=135^o=frac{3pi}{4};$$Получилась абсолютно симметричная картина относительно горизонтальной оси (оси косинусов). (См. Рис. 3). Если согнуть рисунок по горизонтальной оси, то верхняя половина единичной окружности точно совпадет с нижней. Это значит, что (angle{MOA}=angle{FOA}) и (angle{TOA}=angle{NOA}) (углы показаны на рис.3. зелёным цветом).
Тогда согласно рис.3 мы можем выразить искомые углы:
$$angle{AOF}=360^o-angle{FOA}=360^o-angle{MOA}=360^o-45^o=315^o=2pi-frac{pi}{4}=frac{7pi}{4};$$
$$angle{AOT}=360^o-angle{TOA} =360^o-angle{NOA}=360^o-135^o=225^o=2pi-frac{3pi}{4}=frac{5pi}{4};$$ - Углы найдены, добавляем к каждому период (2pi*n) и записываем ответ.
Ответ:
$$x_{1}=frac{5pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=frac{7pi}{4}+2pi*n, quad n in Z;$$
Важное замечание!Напоминаю, что углы на тригонометрической окружности можно отсчитывать от отрезка (OA) и ПО часовой стрелке, только тогда они будут со знаком минус. А для нас это прекрасная новость, ведь тогда:
$$angle{FOA}=-angle{MOA}=-45^o=-frac{pi}{4};$$
$$angle{TOA}=-angle{NOA}=-135^o=-frac{3pi}{4};$$
И ответ на пример №2 можно записать в другом виде через углы (angle{FOA}) и (angle{TOA}), отсчитанным против часовой стрелки:
Ответ:
$$x_{1}=-frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
Абсолютно без разницы в каком виде записать ответ в примере №2, по сути, первый и второй вариант ответа это одно и то же. Напоминаю, что ответы в тригонометрии мы записываем в виде правила, которому подчиняются бесконечное количество углов. Правило одно и то же, и задает одни и те же углы, только разная точка отсчета, к которой прибавляется период (2pi*n.) Попробуйте на бумаге поподставлять различные значения (n) и туда, и туда. Убедитесь сами, что корни будут получаться одинаковые.
Я бы использовал второй вариант написания ответа, на мой взгляд, он легче.
Пример 3
$$sin(x)=1;$$
Решим вот такое интересное тригонометрическое уравнение.
- Рисуем единичную окружность;
- На оси синусов отмечаем значение (1);
- Проводим перпендикуляр к оси синусов через (1);
- Наш перпендикуляр пересечет окружность только в одной точке! На Рис.4. эта точка отмечена как (B);
- Раз у нас всего лишь одна точка, значит и угол будет один. Точка (B) соответствует углу (90^o=frac{3pi}{2});
- Записываем ответ, не забывая про период;
Ответ:(x=frac{3pi}{2}+2pi*n, quad n in Z;)
Пример 4
$$sin(x)=5;$$
Это пример-ловушка. Дело в том, что (sin(x)) – это функция ограниченная. Синус не может принимать значения большие (1) и меньшие (-1):
$$sin(x)in[-1;1];$$
Этот факт следует из определения синуса. Его нужно запомнить и быть внимательным.
Арксинус. Обратная тригонометрическая функция синусу
И разберем последнее типовое тригонометрическое уравнение с синусом:
Пример 5
$$sin(x)=frac{1}{3};$$
Алгоритм решения здесь такой же. Не будем четвертый раз повторяться.
Но здесь есть большая проблема. Дело в том, что значение синуса (frac{1}{3}) не табличное, его нет в таблице стандартных углов! Как же тогда искать углы, синус от которых будет (frac{1}{3})?
Чтобы было возможно решать такие тригонометрические уравнения без калькулятора, люди придумали дополнительную функцию, которую назвали арксинус.
(arcsin(frac{1}{3})) – это обозначение такого угла, синус от которого равен (frac{1}{3}).
$$sin(arcsinleft(frac{1}{3}right))=frac{1}{3};$$
В общем случае (arcsin(a)) – это угол, синус от которого равен (a). Где (ain[-1;1]), так как значения синуса принадлежат промежутку ([-1;1].)
$$sin(arcsin(a))=a;$$
Кстати, для арксинуса справедлива очень важная формула:
$$mathbf{arcsin(-a)=-arcsin(a);}$$
Запомните ее, мы еще с ней встретимся.
В общем, арксинус – это просто обозначение угла. Но так как в предыдущих примерах мы выяснили, что практически любому значению синуса соответствует как минимум два угла, то какой из этих углов это арксинус?
Посмотрите выше на рис. 5. Значению (frac{1}{3}) соответствует два угла (angle{MOA}) и (angle{NOA}), какой именно угол из этих двух будет равен (arcsin(frac{1}{3}))?
Для того, чтобы не было такой неопределённости, и чтобы арксинусу (frac{1}{3}) однозначно соответствовал ровно один угол, придумали ограничения, накладываемые на функцию арксинуса:
$$arcsin(a)in[-frac{pi}{2};frac{pi}{2}];$$
То есть арксинусы – это углы, обязательно лежащие в промежутке ([-frac{pi}{2};frac{pi}{2}].). На рисунке промежуток показан фиолетовым цветом.
Тогда в нашем примере:
$$angle{MOA}=arcsin(frac{1}{3});$$
Для того, чтобы найти (angle{NOA}), нужно просто из геометрических соображений из угла (180^o=pi) вычесть угол (angle{NOB}=angle{MOA}=arcsin(frac{1}{3})):
$$angle{NOA}=pi-arcsin(frac{1}{3});$$
Добавляем к получившимся углам период и получаем:
Ответ:
$$angle{MOA}=arcsin(frac{1}{3})+2pi*n, quad n in Z;$$
$$angle{NOA}=pi-arcsin(frac{1}{3})+2pi*n, quad n in Z.$$
Решение тригонометрического уравнения с косинусом на окружности
На самом деле, уравнения с косинусом мало чем отличаются от уравнений с синусом. Рассмотрим алгоритм решения на примере:
Пример 6
$$cos(x)=frac{1}{2};$$
- Рисуем единичную окружность;
- Отмечаем на линии косинусов (горизонтальная линия) значение (frac{1}{2}) в точке (P);
- Проводим перпендикуляр (a) к линии косинусов через точку (P);
- Перпендикуляр (a) пересечет окружность в точках (K) и (L);
- Точки (K) и (L) соответствуют углам (angle{KOA}) и (angle{LOA});
- Косинус от углов (angle{KOA}) и (angle{LOA}) будет равен (frac{1}{2}) по построению;
- Осталось найти значение этих углов. Смотрим в таблицу стандартных значений и находим, что косинус от угла (60^o=frac{pi}{3}) будет как раз равен (frac{1}{2});
- Тогда, держа в голове, что углы отсчитываются ПРОТИВ часовой стрелки от отрезка (OA) делаем вывод, что (angle{KOA}=60^o=frac{pi}{3};)
- Угол (angle{LOA}) находим из соображения симметрии картинки относительно горизонтальной оси косинусов: (angle{LOA}=-angle{KOA}=-60^o=-frac{pi}{3}.) Знак минус появляется потому что (angle{LOA}) мы отсчитываем от отрезка (OA) ПО часовой стрелке.
- Мы нашли углы, косинус от которых будет равен (frac{1}{2}), добавляем период (2pi*n) и записываем ответ;
Ответ:
$$x_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Тригонометрические уравнения с косинусом легче, чем с синусом: находишь один угол, а второй просто записываешь со знаком минус из горизонтальной симметрии.
Пример 7
$$cos(x)=- frac{sqrt{3}}{2};$$
- Рисуем тригонометрическую окружность;
- Отмечаем на линии косинусов примерное значение (-frac{sqrt{3}}{2}approx-frac{1,7}{2}=-0,85) в точке (F);
- Проводим перпендикуляр к линии косинусов через точку (F);
- Обозначим точки пересечения с окружностью за (M) и (N);
- Точки (M) и (N) соответствуют углам (angle{MOA}) и (angle{NOA});
- Осталось найти значение этих углов. Но у нас опять небольшая проблема: в таблице стандартных углов нет значения (-frac{sqrt{3}}{2}). Зато там есть (frac{sqrt{3}}{2}).
Отметим на той же окружности решение уравнения (cos(x)=frac{sqrt{3}}{2}) (см. Рис. 7), оно будет в правой части окружности, а углы (angle{EOA}) и (angle{TOA}) будут решениями. Из таблицы стандартных углов находим, что косинус от угла (30^o=frac{pi}{6}) будет равен (frac{sqrt{3}}{2}). Значит (angle{EOA}=frac{pi}{6}), а (angle{TOA}=-frac{pi}{6}), если его отсчитать по часовой стрелке.
Обратите внимание, что рисунок симметричен относительно вертикальной оси синусов, что нам дает равенство углов (angle{MOC}=angle{EOA}=30^o=frac{pi}{6}). Теперь можем найти (angle{MOA}):
$$angle{MOA}=180^o-angle{MOC}=180^o-30^o=150^o=pi-frac{pi}{6}=frac{5pi}{6};$$
А угол (angle{NOA}) из геометрических соображений равен (angle{MOA}), но отсчитываем мы его ПО часовой стрелке:
$$angle{NOA}=-angle{MOA}=-frac{5pi}{6};$$ - Мы нашли углы, косинус от которых будет равен (-frac{sqrt{3}}{2}), добавляем период (2pi*n) и записываем ответ;
Ответ:
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{3}+2pi*n, quad n in Z.$$
Пример 8
$$cos(x)=0;$$
- Как обычно, рисуем окружность;
- На оси косинусов отмечаем значение (0), оно лежит прямо в пересечении осей синуса и косинуса;
- Проводим перпендикуляр к оси косинусов через точку (0). Будьте внимательны, этот перпендикуляр полностью совпадет с осью синусов и пересечет окружность в точках (B) и (D;)
- Углы (angle{BOA}) и (angle{DOA}) искомые;
- Точки (B) и (D) соответствуют на окружности углам (90^o=frac{pi}{2}) и (-90^o=-frac{3pi}{2}.)
- Учитывая период, записываем ответ:
Ответ:
$$x_{1}=frac{pi}{2}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{2}+2pi*n, quad n in Z;$$
Арккосинус. Обратная тригонометрическая функция косинусу
По аналогии с арксинусом существует функция обратная косинусу. Каждый раз, когда вам встречается не табличное значение, придется использовать арккосинус. Познакомимся с ним на примере:
Пример 9
$$cos(x)=frac{1}{5};$$
Как обычно, отметим на оси косинусов (frac{1}{5}) и нарисуем соответствующие этому значению углы (angle{KOA}) и (angle{LOA}).
В таблице значения (frac{1}{5}) нет. И чтобы этот пример можно было решить, люди придумали функцию арккосинуса, при помощи которой обозначают нестандартные углы.
(arccos(frac{1}{5})) – это обозначение угла, косинус от которого будет равен (frac{1}{5}).
$$cos(arccosleft(frac{1}{5}right))=frac{1}{5};$$
В общем виде (arccos(a)) – это угол, косинус от которого будет равен (a), где (ain[-1;1]), ведь значения косинуса лежат в промежутке ([-1;1].)
Так как почти любому значению косинуса соответствует минимум две точки (два угла) на окружности, то для того, чтобы понять, какой именно угол из этих двух будет арккосинусом, на функцию арккосинус накладываются определенные ограничения:
$$arccos(a)in[0;pi];$$
То есть, арккосинус – это углы, лежащие в верхней половине единичной окружности в промежутке ([0;pi].)
Кстати, для арккосинуса справедлива формула:
$$mathbf{arccos(-a)=pi-arccos(a);}$$
Возвращаясь к нашему примеру:
$$angle{KOA}=arccos(frac{1}{5});$$
А для того, чтобы найти второй угол (angle{LOA}), нужно заметить, что:
$$angle{LOA}=-angle{KOA}=-arccos(frac{1}{5});$$
Если считать угол по часовой стрелке.
Не забываем про период и записываем ответ:
Ответ:
$$angle{KOA}=arccos(frac{1}{5})+2pi*n, quad n in Z;$$
$$angle{LOA}=-arccos(frac{1}{5}+2pi*n, quad n in Z;$$
Важно! Значения косинуса, так же, как и синуса, принадлежат промежутку ([-1;1]). Если вы встретите уравнение по типу (cos(x)=3), то оно не будет иметь решений.
Тригонометрическое уравнение с тангенсом на окружности
Тангенс и котангенс на единичной окружности ведут себя несколько иначе, чем синус и косинус. Кто не помнит, как тангенс и котангенс отображаются на окружности и какими свойствами обладают, рекомендую повторить.
Как обычно, будем учиться на примерах:
Пример 10
$$tg(x)=1;$$
- На тригонометрической окружности необходимо нарисовать ось тангенсов. Напоминаю, что она параллельна оси синусов и проходит через точку (A);
- На оси тангенсов отмечаем значение (1), обозначим эту точку за (K);
- Соединим точку (K) с центром окружности и продлим до пересечения с окружностью;
- Получим две точки на окружности (M) и (N);
- Они соответствуют углам (angle{MOA}) и (angle{NOA}), тангенс от которых будет равен (1);
- По таблице стандартных углов находим, что тангенс равен (1) от угла (45^o=frac{pi}{4}), судя по рисунку №10, это будет угол (angle{MOA});
- Угол (angle{NOA}) можно найти по формуле:
$$angle{NOA}=180^o+angle{MOA}=pi+angle{MOA}=pi+frac{pi}{4}=frac{5pi}{4};$$
Это следует из окружности, посмотрите на Рис.10. Наши два угла отличаются ровно на (180^o=pi) градусов. Это важный момент, который дает нам возможность записывать ответ в одну строчку, а не в две, как у синуса и косинуса:
$$x=frac{pi}{4}+pi*n, quad n in Z;$$
Это весь ответ, больше ничего писать не нужно. Обратите внимание на период, здесь он у нас (pi*n), а не (2pi*n), как было у синуса и косинуса. Подставляя различные значения (n), вы будет прибавлять к (frac{pi}{4}):
$$n=1 qquad x_{1}=frac{pi}{4}+pi;$$
Смотрите, прибавив (pi) при (n=1) вы из точки (M) попали в точку (N).
$$n=2 qquad x_{2}=frac{pi}{4}+2pi;$$
При (n=2) мы опять вернулись из точки (N) в точку (M).
$$n=3 qquad x_{1}=frac{pi}{4}+3pi;$$
При (n=3) попадаем из (M) в точку (N).
Другими словами, период (pi*n) означает, что ваши корни лежат на окружности с периодом в половину окружности, а правило (x=frac{pi}{4}+pi*n, quad n in Z;) покрывает обе точки и (M), и (N).
Главный вывод в том, что у простейшего уравнения с тангенсом записывается в ответ только одна точка (любая) и прибавляется период (pi*n). Этот факт можно просто запомнить.
Ответ: (x=frac{pi}{4}+pi*n, quad n in Z.)
Арктангенс. Обратная тригонометрическая функция тангенсу
По аналогии с арксинусом и арккосинусом существует и арктангенс – функция, обратная тангенсу. Она необходима, когда перед вами нестандартные (не табличные) значения тангенса.
В общем виде арктангенс от некоторого числа (a) – это угол, тангенс от которого равен (a):
$$tg(arctg(a))=a; qquad ain(-infty;+infty); $$
$$arctg(a)in(-frac{pi}{2};frac{pi}{2}).$$
Обратите внимание, что значения арктангенса всегда по определению лежат в промежутке ((-frac{pi}{2};frac{pi}{2})): в правой полуокружности.
Кстати, для арктангенса справедлива формула:
$$mathbf{arctg(-a)=-arctg(a)};$$
Пример 11
$$tg(x)=3;$$
- Рисуем единичную окружность;
- Отмечаем на оси тангенсов значение (3), обозначим за точку (K);
- Через точку (K) и центр окружности проводим прямую, которая пересечет окружность в двух точках (M) и (N);
- В таблице стандартных углов тангенс, равный (3), вы не найдете. И тут нам пригодится арктангенс. Арктангенсом мы будем называть угол, тангенс от которого равен 3-м. Поэтому угол (angle{MOA}=arctg(3),) согласно определению арктангенса;
- Угол (angle{NOA}) можно найти по формуле:
$$angle{NOA}=angle{MOA}+180^0=angle{MOA}+pi=arctg(3)+pi;$$ - Но на самом деле, оба угла (angle{MOA}) и (angle{MOA}) для ответа нам не нужны. В ответ мы можем записать любой из них и указать период (pi*n), который покроет оба угла;
Ответ: (x=arctg(3)+pi*n, quad n in Z.)
Тригонометрическое уравнение с котангенсом
Уравнения с котангенсом очень похожи на уравнения с тангенсом с одним исключением: ось котангенсов на единичной окружности параллельна горизонтальной оси косинусов, полностью ее дублирует и проходит через точку (B).
Пример 12
$$ctg(x)=sqrt{3};$$
- Рисуем единичную окружность;
- Проводим через точку (B) ось котангенсов параллельно горизонтальной оси;
- На оси котангенсов отмечаем значение (sqrt{3}approx1,7), обозначим за точку (P);
- Соединяем точку (P) с центром окружности и продляем до пересечения с ней в двух точках: (L) и (F);
- Котангенс от углов (angle{LOA}) и (angle{FOA}) и будет равен (sqrt{3});
- В таблице стандартных углов находим, что (ctg(frac{pi}{6})=sqrt{3};)
- Согласно рисунку (angle{LOA}=frac{pi}{6}), а угол (angle{FOA}=frac{pi}{6}+pi=frac{7pi}{6};)
- Как и с тангенсом, оба угла нам не нужно, достаточно в ответе указать одну точку с периодом (pi*n);
Ответ: (x=frac{pi}{6}+pi*n, quad n in Z.)
В простейших уравнениях с котангенсом в ответе мы указываем любой из двух получившихся углов, при этом не забываем про период (pi*n).
Разберем еще уравнение с отрицательной правой частью:
Пример 13
$$ctg(x)=-1;$$
Отметим на тригонометрической окружности ось котангенсов и на ней значение (-1). Так подробно расписывать решение, как в прошлых примерах, мы не будем, идея уже должна быть давно понятна.
На рисунке искомыми углами будут (angle{MOA}) и (angle{NOA}). Мы не можем воспользоваться таблицей стандартных углов, так как там нет значения котангенса (-1), но зато есть значение (1.)
Решим на этой же самой окружности уравнение (ctg(x)=1). Котангенс от углов (angle{KOA}) и (angle{LOA}) будет равен (1). Из таблицы стандартных углов делаем вывод, что (angle{KOA}=frac{pi}{4}).
Так как получившийся рисунок симметричен относительно вертикальной оси синусов, то из геометрических соображений:
$$angle{KOA}=angle{MOC};$$
Тогда:
$$angle{MOA}=pi-angle{MOC}=pi-angle{KOA}=pi-frac{pi}{4}=frac{3pi}{4};$$
Кроме того, наш рисунок симметричен относительно горизонтальной оси косинусов. Из чего легко сделать вывод:
$$angle{NOA}=-angle{KOA}=-frac{pi}{4};$$
Знак минус возникает из-за того, что мы отсчитываем угол (angle{NOA}) ПО часовой стрелке.
Записываем ответ, указывая любой из углов (angle{MOA}) или (angle{NOA}) с учетом периода (pi*n).
Ответ: (x=-frac{pi}{4}+pi*n, quad n in Z.)
Арккотангенс. Обратная тригонометрическая функция котангенсу
И нам осталось обсудить последнюю тригонометрическую функцию в школьной программе: арккотангенс.
Как и другие обратные функции, арккотангенс от некоторого числа (a) – это угол, котангенс от которого будет равен (a):
$$tg(arcctg(a))=a; qquad ain(-infty;+infty); $$
$$arcctg(a)in(0;pi).$$
Обратите внимание на ограничения, которые по определению накладываются на арккотангенс: его значения принадлежат промежутку ((0;pi)), то есть это углы, лежащие в верхней половине окружности. Эти ограничения необходимы для однозначности функции арккотангенса, так как любому значению котангенса всегда соответствует две точки на окружности, а значит минимум два угла (в верхней и нижней полуокружностях).
Кстати, для арккотангенса справедлива формула:
$$mathbf{arcctg(-a)=pi-arcctg(a);}$$
Арккотангенс используется, когда в уравнении встречаются нестандартные значения:
Пример 14
$$ctg(x)=5;$$
Отметим все на окружности. Искомыми углами будут (angle{MOA}) и (angle{KOA}).
Так как значение (5) нестандартное, то нам придется воспользоваться функцией арккотангенса: (arcctg(5)).
На нашей окружности (angle{MOA}=arcctg(5)) так как именно он лежит в верхней половине окружности.
Второй угол, как и во всех уравнениях с тангенсом и котангенсом искать совсем не обязательно, но для тренировки сделаем это:
$$angle{KOA}=pi+arcctg(5);$$
И записываем в ответ любой из этих углов с периодом (pi*n).
Ответ: (x=arcctg(5)+pi*n, quad n in Z.)
Формулы для решения тригонометрических уравнений
Мы разобрали решения всех основные типы простейших тригонометрических уравнений при помощи единичной окружности. Я бы рекомендовал всегда решать именно при помощи окружности, это очень полезно для понимания.
А сейчас мы запишем формулы, при помощи которых можно решать уравнения без единичной окружности.
Пусть у нас есть простейшие тригонометрические уравнения:
$$mathbf{sin(x)=a;}$$
где (a) некоторое число, удовлетворяющее условию (ain[-1;1]);
Тогда решением этого уравнения будет:
$$mathbf{x=(-1)^n*arcsin(a)+pi*n, quad n in Z;}$$
$$mathbf{cos(x)=a;}$$
где (a) некоторое число, удовлетворяющее условию (ain[-1;1]);
Тогда решением этого уравнения будет:
$$mathbf{x=pmarccos(a)+2pi*n, quad n in Z;}$$
$$mathbf{tg(x)=a;}$$
где (a) некоторое число, удовлетворяющее условию (ain(-infty;+infty));
Тогда решением этого уравнения будет:
$$mathbf{x=arctg(a)+pi*n, quad n in Z;}$$
$$mathbf{ctg(x)=a;}$$
где (a) некоторое число, удовлетворяющее условию (ain(-infty;+infty));
Тогда решением этого уравнения будет:
$$mathbf{x=arcctg(a)+pi*n, quad n in Z;}$$
Можно просто запомнить формулы и решать уравнения с их помощью.
И полезно помнить формулы, которые мы вводили, когда давали определение обратных функций:
$$mathbf{arcsin(-a)=-arcsin(a);}$$
$$mathbf{arccos(-a)=pi-arccos(a);}$$
$$mathbf{arctg(-a)=-arctg(a);}$$
$$mathbf{arcctg(-a)=pi-arcctg(a).}$$
Рассмотрим примеры:
Пример 15
$$sin(x)=frac{1}{2};$$
Сразу выпишем общую формулу ответа:
$$x=(-1)^n*arcsin(a)+pi*n, quad n in Z;$$
где (a=frac{1}{2});
$$x=(-1)^n*arcsin(frac{1}{2})+pi*n, quad n in Z;$$
В таком виде лучше не оставлять. Если вы можете посчитать, чему равен арксинус, то это обязательно нужно сделать.
Арксинус от (frac{1}{2}), согласно определению, это угол, синус от которого равен (frac{1}{2}). По таблице стандартных углов мы видим, что синус равен (frac{1}{2}) от угла (frac{pi}{6}):
$$arcsin(frac{1}{2})=frac{pi}{6};$$
$$x=(-1)^n*frac{pi}{6}+pi*n, quad n in Z;$$
В таком виде уже можно записывать ответ:
Ответ: (x=(-1)^n*frac{pi}{6}+pi*n, quad n in Z.)
Пример 16
$$cos(x)=-frac{sqrt{2}}{2};$$
Общий вид решения:
$$x=pmarccos(a)+2pi*n, quad n in Z;$$
где (a=-frac{sqrt{2}}{2});
$$x=pmarccos(-frac{sqrt{2}}{2})+2pi*n, quad n in Z;$$
Арккосинус от (-frac{sqrt{2}}{2}) это угол, косинус от которого будет равен (-frac{sqrt{2}}{2}). Но в таблице нет значения (-frac{sqrt{2}}{2}), зато есть (frac{sqrt{2}}{2}).
Используя свойство арккосинуса:
$$arccos(-a)=pi-arccos(a);$$
Можно записать:
$$x=pm(pi-arccos(frac{sqrt{2}}{2}))+2pi*n, quad n in Z;$$
Учитывая:
$$arccos(frac{sqrt{2}}{2})=frac{pi}{4};$$
Подставляем:
$$x=pm(pi-frac{pi}{4})+2pi*n, quad n in Z;$$
$$x=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Ответ: (x=pmfrac{3pi}{4}+2pi*n, quad n in Z.)
Пример 17
$$tg(x)=-sqrt{3};$$
Общий вид решения:
$$x=arctg(a)+pi*n, quad n in Z;$$
где (a=-sqrt{3});
$$x=arctg(-sqrt{3})+pi*n, quad n in Z;$$
Арктангенс от (-sqrt{3}) это угол, тангенс от которого равен (-sqrt{3}). В таблице опять нет такого значения (-sqrt{3}), но есть положительное (sqrt{3}), арктангенс от которого можно посчитать:
$$arctg(sqrt{3})=frac{pi}{3};$$
Учитывая свойство арктангенса:
$$arctg(-a)=-arctg(a);$$
Подставляем в нашу формулу:
$$x=-arctg(sqrt{3})+pi*n, quad n in Z;$$
$$x=-frac{pi}{3}+pi*n, quad n in Z;$$
Ответ: (x=-frac{pi}{3}+pi*n, quad n in Z.)
Замена переменной в тригонометрических уравнениях
Замена выражения под тригонометрической функцией
Мы научились решать простейшие уравнения. И на этом строится решение всех остальных тригонометрических уравнений. Они все так или иначе сводятся к решению простейших. И один из способов – это введение замены переменной.
Вы должны были с этим регулярно сталкиваться в младших классах при решении, например, биквадратных уравнений. Все дальнейшие рассуждения предполагают, что вы знаете, что такое замена переменной. Итак, разберем пример:
Пример 18
$$sin(2x)=frac{sqrt{3}}{2};$$
Обратите внимание, что теперь у нас под синусом стоит не просто (x), а целое выражение. Давайте избавимся от него, убрав (2x) в замену: пусть (t=2x).
$$sin(t)=frac{sqrt{3}}{2};$$
Теперь наше уравнение превратилось в простейшее тригонометрическое. Решаем его относительно переменной (t) (вы можете решать при помощи единичной окружности или по готовым формулам, как вам удобнее. Я же буду просто выписывать ответ):
$$t_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$t_{2}=frac{2pi}{3}+2pi*n, quad n in Z;$$
На этом решение не заканчивается. Мы нашли значения (t), а нам надо найти (x). Делаем обратную замену, вспоминая, что (t=2x):
$$2x_{1}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$2x_{2}=frac{2pi}{3}+2pi*n, quad n in Z;$$
И просто выражаем из получившихся выражений (x), для этого разделим левую и правую часть равенства на (2):
$$frac{2x_{1}}{2}=frac{frac{pi}{3}+2pi*n}{2}, quad n in Z;$$
$$frac{2x_{2}}{2}=frac{frac{2pi}{3}+2pi*n}{2}, quad n in Z;$$
$$x_{1}=frac{1}{2}*frac{pi}{3}+pi*n, quad n in Z;$$
$$x_{2}=frac{1}{2}*frac{2pi}{3}+pi*n, quad n in Z;$$
Обратите внимание, что период тоже не забываем поделить на (2).
Ответ:
$$x_{1}=frac{pi}{6}+pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{3}+pi*n, quad n in Z.$$
Аналогичным образом можно решать тригонометрические уравнения с более сложным подтригонометрическим выражением:
Пример 19
$$tg(frac{2x+pi}{3})=1;$$
Под тангенсом тут стоит целая дробь, зависящая от (x). Засунем всю эту дробь в замену:
$$t=frac{2x+pi}{3};$$
Уравнение примет вид:
$$tg(t)=1;$$
Решением этого простейшего уравнения будет:
$$t=frac{pi}{4}+pi*n, quad n in Z;$$
Делаем обратную замену, вместо (t) подставляем (frac{2x+pi}{3}):
$$frac{2x+pi}{3}=frac{pi}{4}+pi*n, quad n in Z;$$
И выражаем отсюда (x). Домножим равенство на (3):
$$2x+pi=3*(frac{pi}{4}+pi*n), quad n in Z;$$
$$2x+pi=frac{3pi}{4}+3pi*n, quad n in Z;$$
Перенесем (pi) направо:
$$2x=-pi+frac{3pi}{4}+3pi*n, quad n in Z;$$
Приведем подобные слагаемые:
$$2x=-frac{pi}{4}+3pi*n, quad n in Z;$$
И разделим на (2):
$$x=-frac{pi}{8}+frac{3}{2}*pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{8}+frac{3}{2}*pi*n, quad n in Z;$$
Замена всей тригонометрической функции
Что делать с подтригонометрическим выражением, мы разобрались. Теперь решим пример на замену, при помощи которой тригонометрическое уравнение сводится к квадратному.
Пример 20
$$2*sin^2(x)+sin(x)-1=0;$$
Обращаем внимание на одинаковое выражение (sin(x)). Сделаем замену:
$$t=sin(x);$$
$$2t^2+t-1=0;$$
Получили обыкновенное квадратное уравнение, которое решается через дискриминант:
$$D=1-4*2*(-1)=9;$$
$$t_{1}=frac{-1+3}{4}=frac{1}{2};$$
$$t_{2}=frac{-1-3}{4}=-1;$$
Делаем обратную замену и получаем два простейших тригонометрических уравнения. Первое:
$$sin(x)=frac{1}{2};$$
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Второе:
$$sin(x)=-1;$$
$$x_{3}=frac{3pi}{2}+2pi*n, quad n in Z;$$
Записываем ответ из трех наборов решений.
Ответ:
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{3}=frac{3pi}{2}+2pi*n, quad n in Z;$$
Тригонометрические уравнения в ЕГЭ
В ЕГЭ в большинстве тригонометрических уравнений нужно уметь преобразовать исходное уравнение и сделать замену. Для того, чтобы правильно преобразовывать уравнение, необходимо хорошо знать тригонометрические формулы и помнить главное правило:
Стараться свести уравнение к виду, в котором все тригонометрические функции и выражения, от которых они берутся, одинаковы.
Другими словами, нужно сделать так, чтобы во всем уравнении везде был, например, только синус от (x).
Рассмотрим несложный реальный пример из ЕГЭ.
Пример 21
$$2cos^2(x)+sin(x)+1=0;$$
Смотрите, в уравнении сразу две тригонометрические функции и синус, и косинус. Это плохо. Нужно сделать так, чтобы была только одна из них. Тут нам поможет основное тригонометрическое тождество:
$$sin^2(x)+cos^2(x)=1;$$
$$cos^2(x)=1-sin^2(x);$$
И подставим в исходное уравнение:
$$1-sin^2(x)+sin(x)+1=0;$$
Приведем подобные слагаемые:
$$-sin^2(x)+sin(x)+2=0;$$
Теперь в уравнении везде (sin(x)), можно сделать замену:
$$t=sin(x);$$
Уравнение примет вид:
$$-t^2+t+2=0;$$
Находим корни квадратного уравнения:
$$D=9;$$
$$t_{1}=frac{-1+3}{-2}=-1;$$
$$t_{2}=frac{-1-3}{-2}=2;$$
Обратная замена:
$$sin(x)=-1;$$
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
И второе уравнение:
$$sin(x)=2;$$
Оно не имеет решений, так как синус может принимать значения только из промежутка ([-1;1]).
Ответ:
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
Пример 22
$$2*sin^2(pi+x)-5*cos(frac{pi}{2}+x)+2=0;$$
Этот пример уже сложнее: во-первых, под тригонометрическими функциями стоят какие-то непонятные, да еще и разные, выражения; во-вторых, в уравнении у нас и синус, и косинус, а должно быть что-то одно.
Читатель, который знаком с формулами приведения, обязательно должен был заметить, что под синусом и косинусом стоят не просто какие-то выражения, а это формулы приведения. Выпишем их отдельно и преобразуем:
$$sin(pi+x)=-sin(x);$$
$$cos(frac{pi}{2}+x)=-sin(x);$$
Подставим преобразования в исходное уравнение.
Внимание! Когда мы будем подставлять (-sin(x)) вместо (sin(pi+x)), то знак минус сгорит, так как у нас (sin(pi+x)) под квадратом. Это очень частая ошибка.
$$2*(-sin(x))^2-5*(-sin(x))+2=0;$$
$$2*sin^2(x)+5*sin(x)+2=0;$$
Применив формулы привидения, у нас чудесным образом получилось уравнение, в котором можно сделать замену:
$$t=sin(x);$$
$$2*t^2+5*t+2=0;$$
$$D=9;$$
$$t_{1}=frac{-5+3}{4}=-frac{1}{2};$$
$$t_{2}=frac{-5-3}{4}=-2;$$
Обратная замена:
$$sin(x)=-frac{1}{2};$$
$$x_{1}=-frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
И второе уравнение:
$$sin(x)=-2;$$
Решений не имеет, так как (sin(x)in[-1;1]) по определению.
Ответ:
$$x_{1}=-frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Однородные тригонометрические уравнения
Мы выяснили, что для того, чтобы решить уравнение, необходимо привести все к одинаковым тригонометрическим функциям от одинаковых аргументов. Но иногда сделать это затруднительно. Например, как вы будете решать вот такое уравнение:
Пример 23
$$sin(x)+cos(x)=0;$$
Нет такой удобной формулы, по которой можно превратить синус в косинус или наоборот. Хотя, конечно, можно воспользоваться основным тригонометрическим тождеством и выразить оттуда синус через косинус:
$$sin^2(x)+cos^2(x)=1;$$
$$sin^2(x)=1-cos^2(x);$$
$$sin(x)=pmsqrt{1-cos^2(x)};$$
Подставив это выражение вместо синуса в исходное уравнение, мы получим в уравнении одни косинусы, но уравнение станет иррациональным (то есть с корнем). Его можно решить, но это достаточно сложно. И так никто не делает.
Оптимальным решением здесь будет поделить исходное уравнение на синус или косинус, давайте поделим на косинус:
$$frac{sin(x)+cos(x)}{cos(x)}=frac{0}{cos(x)};$$
$$frac{sin(x)}{cos(x)}+frac{cos(x)}{cos(x)}=0;$$
$$tg(x)+1=0;$$
$$tg(x)=-1;$$
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Рассмотрим еще один пример:
Пример 24
$$sin(x)+sqrt{3}*cos(x)=0;$$
Аналогично предыдущему примеру поделим все уравнение на (sin(x)):
$$1+sqrt{3}*frac{cos(x)}{sin(x)}=0;$$
$$1+sqrt{3}*ctg(x)=0;$$
$$sqrt{3}*ctg(x)=-1;$$
$$ctg(x)=-frac{1}{sqrt{3}};$$
$$x=frac{pi}{3}+pi*n, quad n in Z;$$
Ответ:
$$x=frac{pi}{3}+pi*n, quad n in Z;$$
Мы рассмотрели два примера так называемых однородных уравнений первой степени. Рассмотрим пример на однородное уравнение второй степени.
Пример 25
$$3sin^2(x)+sin(x)*cos(x)=2cos^2(x);$$
Здесь тоже будем применять деление, только в этот раз будем делить каждое слагаемое на (cos^2(x)) (можно поделить и на (sin^2(x)), это не имеет значения):
$$3frac{sin^2(x)}{cos^2(x)}+frac{sin(x)*cos(x)}{sin^2(x)}=frac{2cos^2(x)}{cos^2(x)};$$
$$3tg^2(x)+tg(x)=2;$$
Теперь можно сделать замену (t=tg(x)):
$$3t^2+t=2;$$
$$3t^2+t-2=0;$$
$$D=1+24=25;$$
$$t_{1}=frac{-1-5}{6}=-1;$$
$$t_{2}=frac{-1+5}{6}=frac{2}{3};$$
Обратная замена:
Первое уравнение:
$$tg(x)=-1;$$
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
Второе уравнение:
$$tg(x)=frac{2}{3};$$
$$x=arctg(frac{2}{3})+pi*n, quad n in Z;$$
Ответ:
$$x=-frac{pi}{4}+pi*n, quad n in Z;$$
$$x=arctg(frac{2}{3})+pi*n, quad n in Z;$$
Есть нюанс, на котором школьники часто сыпятся. Освоив метод деления, ученик начинает пытаться решить тригонометрические уравнения только через него и на экзамене, решив вроде все правильно, получает 0 баллов.
Оказывается, что не всякое уравнение можно разделить на выражение зависящее от (x). Посмотрите пример №26, это убережет вас от подобных ошибок на экзамене.
Пример 26
$$sin^2(x)+sin(x)=0;$$
Разделим уравнение на (sin(x)):
$$sin(x)+1=0;$$
$$sin(x)=-1;$$
$$x=frac{3pi}{2}+2pi*n, quad n in Z;$$
И тут, кажется, можно записывать ответ, но это неверное решение уравнения, так решать нельзя. Достаточно легко заметить, что (sin(x)=0) тоже будет являться решением исходного уравнения. Подставьте вместо (sin(x)) ноль и получите верное равенство. А в нашем решении такого ответа нет, значит где-то по дороге мы потеряли корни. А потеряли мы их именно в тот момент, когда сделали деление.
Запомните важное правило! Делить уравнение можно только тогда, когда выражение, на которое вы делите, равное нулю не будет корнем исходного уравнения.
В нашем случае мы делим на (sin(x)), но (sin(x)=0) является решением, поэтому делить нельзя.
Чтобы все-таки решить это уравнение правильно, нужно воспользоваться вынесением общего множителя за скобки.
Вынесение общего множителя в тригонометрических уравнениях
Еще один распространенный на ЕГЭ тип тригонометрических уравнений, в которых необходимо вынести общий множитель.
Пример 27
$$sin(2x)-2sin^2(x)=0;$$
В этом уравнении только одна тригонометрическая функция — (sin(x)). Но под синусами стоят разные выражения. Поэтому избавимся от двойного угла под синусом при помощи формулы синуса двойного угла:
$$sin(2x)=2sin(x)*cos(x);$$
Уравнение примет вид:
$$2sin(x)*cos(x)-2sin^2(x)=0;$$
Замечаем общий множитель (2*sin(x)), вынесем его за скобки:
$$2*sin(x)*(cos(x)-sin(x))=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Уравнение разбивается на два:
Либо:
$$2sin(x)=0;$$
$$sin(x)=0;$$
$$x_{1}=0+2pi*n=2pi*n, quad n in Z;$$
$$x_{2}=pi+2pi*n, quad n in Z;$$
(Кстати, эти два решения можно объединить в одно: (x=0+pi*n=pi*n, quad n in Z;))
Либо второе уравнение:
$$cos(x)-sin(x)=0;$$
Это уравнение решается при помощи деления. Разделим левую и правую часть уравнения на (cos(x)):
$$frac{cos(x)-sin(x)}{cos(x)}=frac{0}{cos(x)};$$
$$1-frac{sin(x)}{cos(x)}=0;$$
$$1-tg(x)=0;$$
$$tg(x)=1;$$
$$x=frac{pi}{4}+pi*n, quad n in Z;$$
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{4}+pi*n, quad n in Z;$$
Пример 28
$$2cos(frac{pi}{2}-x)=tg(x);$$
Сразу замечаем формулу приведения под косинусом:
$$cos(frac{pi}{2}-x)=sin(x);$$
Подставляем в исходное уравнение
$$2sin(x)=tg(x);$$
Распишем тангенс по определению:
$$tg(x)=frac{sin(x)}{cos(x)};$$
$$2sin(x)=frac{sin(x)}{cos(x)};$$
$$2sin(x)-frac{sin(x)}{cos(x)}=0;$$
И здесь тоже будет общий множитель (sin(x)):
$$sin(x)*(2-frac{1}{cos(x)})=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
Первый множитель:
$$sin(x)=0;$$
$$x_{1}=0+pi*n=pi*n, quad n in Z;$$
Второй множитель:
$$2-frac{1}{cos(x)}=0;$$
Приведем к общему знаменателю:
$$frac{2cos(x)}{cos(x)}-frac{1}{cos(x)}=0;$$
$$frac{2cos(x)-1}{cos(x)}=0;$$
Дробь равна нулю, когда числитель равен нулю – избавляемся от знаменателя:
$$2cos(x)-1=0;$$
$$2cos(x)=1;$$
$$cos(x)=frac{1}{2};$$
$$x_{2}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{3}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{2}=frac{pi}{3}+2pi*n, quad n in Z;$$
$$x_{3}=-frac{pi}{3}+2pi*n, quad n in Z;$$
Метод группировки в тригонометрических уравнениях
Рассмотрим еще уравнение, которое было на ЕГЭ 2015 года на метод группировки. Тоже нужно обязательно это знать. Сам метод, если кто не знает, сводится, по сути, к вынесению общего множителя за скобки, только немного сложнее.
Пример 29
$$sin(2x)+sqrt{2}sin(x)=2cos(x)+sqrt{2};$$
Избавляемся от двойного угла:
$$2*sin(x)cos(x)+sqrt{2}sin(x)=2cos(x)+sqrt{2};$$
И перенесем все в левую часть:
$$2*sin(x)cos(x)+sqrt{2}sin(x)-2cos(x)-sqrt{2}=0;$$
У нас 4 слагаемых, сгруппируем их попарно: 1-е со 2-м, а 3-е с 4-м, и вынесем в каждой паре общий множитель:
$$sin(x)(2cos(x)+sqrt{2})-1(2cos(x)+sqrt{2})=0;$$
У 3-го и 4-го слагаемых я вынес за скобки (-1).
Теперь обратите внимание, что в скобках получились идентичные выражения, то есть эти скобки абсолютно одинаковые. Вынесем эту общую скобку за скобку!
$$(2cos(x)+sqrt{2})(sin(x)-1)=0;$$
Вот мы и сгруппировали, теперь приравниваем каждый множитель к нулю:
Первый множитель:
$$2cos(x)+sqrt{2}=0;$$
$$cos(x)=frac{-sqrt{2}}{2};$$
$$x_{1}=frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
Второй множитель:
$$sin(x)-1=0;$$
$$sin(x)=1;$$
$$x_{3}=frac{pi}{2}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1}=frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{3pi}{4}+2pi*n, quad n in Z;$$
$$x_{3}=frac{pi}{2}+2pi*n, quad n in Z;$$
ОДЗ в тригонометрических уравнениях
С областью допустимых значений мы сталкиваемся в уравнениях и неравенствах, в которых есть знаменатели, корни и логарифмы.
Тригонометрические уравнения не исключение, в них тоже встречается все вышеперечисленное. И в этом случае мы вынуждены не забывать про ограничения и выписывать ОДЗ перед тем, как решать.
Пример 30
$$frac{2sin^2(x)-sin(x)}{2cos(x)-sqrt{3}}=0;$$
В этом уравнении есть знаменатель, при некоторых значениях (x) он может быть равен (0), а тогда у нас будет деление на 0, что запрещено правилами математики. Поэтому надо исключить такие значения (x). Посмотрим, при каких (x) знаменатель равен (0):
$$2cos(x)-sqrt{3}=0;$$
$$cos(x)=frac{sqrt{3}}{2};$$
$$x_{1}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{6}+2pi*n, quad n in Z;$$
Мы получили значения, которые (x) не может принимать, так как возникает деление на (0). Другими словами, мы нашли ОДЗ.
Теперь решим исходное уравнение:
$$frac{2sin^2(x)-sin(x)}{2cos(x)-sqrt{3}}=0;$$
Дробь равна (0), когда числитель равен (0). Избавляемся от знаменателя и приравниваем числитель к (0):
$$2sin^2(x)-sin(x)=0;$$
Вынесем общий множитель:
$$sin(x)(2sin(x)-1)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
Первый:
$$sin(x)=0;$$
$$x_{1}==pi*n, quad n in Z;$$
Второй множитель:
$$2sin(x)-1=0;$$
$$sin(x)=frac{1}{2};$$
$$x_{2}=frac{pi}{6}+2pi*n, quad n in Z;$$
$$x_{3}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Получилось три набора решений, но не все они подходят. Вспоминаем про ОДЗ и видим, что решение (x_{2}=frac{pi}{6}+2pi*n, quad n in Z;) не удовлетворяет ОДЗ, так как при этих значениях (x) возникает деление на (0). Исключаем его из ответа.
Ответ:
$$x_{1}=pi*n, quad n in Z;$$
$$x_{3}=frac{5pi}{6}+2pi*n, quad n in Z;$$
Пример 31
$$frac{sin(2x)}{cos(frac{pi}{2}+x)}=sqrt{3};$$
Найдем ОДЗ:
$$cos(frac{pi}{2}+x)=0;$$
Сделаем замену, пусть (t=frac{pi}{2}+x):
$$cos(t)=0;$$
$$t=frac{pi}{2}+pi*n, quad n in Z;$$
Обратная замена:
$$frac{pi}{2}+x=frac{pi}{2}+pi*n, quad n in Z;$$
$$x=pi*n, quad n in Z;$$
Это и будет наше ОДЗ, (x) не может принимать значения (pi*n, quad n in Z), так как при этих (x) будет деление на (0).
А теперь приступим непосредственно к решению исходного уравнения:
$$frac{sin(2x)}{cos(frac{pi}{2}+x)}=sqrt{3};$$
Используем формулы приведения, чтобы упростить знаменатель. И формулу двойного угла в числителе:
$$frac{2sin(x)*cos(x)}{-sin(x)}=sqrt{3};$$
$$-2cos(x)=sqrt{3};$$
$$cos(x)=-frac{sqrt{3}}{2};$$
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Смотрим на ОДЗ и видим, что оба набора решения нам подходят, пересечения с ОДЗ не случилось. Записываем ответ:
Ответ:
$$x_{1}=frac{5pi}{6}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{5pi}{6}+2pi*n, quad n in Z;$$
Пример 32
$$(tg^2(x)-1)*sqrt{13cos(x)}=0;$$
В этом уравнении есть квадратный корень, а значит подкоренное выражение не может быть меньше нуля, невозможно взять корень из отрицательного числа. ОДЗ будет выглядеть:
$$13cos(x)ge0;$$
$$cos(x)ge0;$$
Получили тригонометрическое неравенство, которое мы решать еще не умеем. Более того, в школах часто совсем не проходят тему тригонометрических неравенств. Поэтому постараемся решить исходя из логики при помощи единичной окружности.
Если посмотреть на рисунок, то видно, что косинус будет положительным от углов, лежащих в правой половине окружности. Закрашенная часть круга удовлетворяет ОДЗ, а не закрашенная – нет. Запомним это и начнем решать исходное уравнение:
$$(tg^2(x)-1)*sqrt{13cos(x)}=0;$$
Из произведения двух множителей получаем два уравнения. Первое:
$$tg^2(x)-1=0;$$
$$tg(x)=pm1;$$
Обратите внимание на (pm), из-за квадрата будет два решения. Будьте осторожны!
$$tg(x)=1;$$
$$x_{1}=frac{pi}{4}+pi*n, quad n in Z;$$
$$tg(x)=-1;$$
$$x_{2}=-frac{pi}{4}+pi*n, quad n in Z;$$
Второе уравнение:
$$sqrt{13cos(x)}=0;$$
$$13cos(x)=0;$$
$$cos(x)=0;$$
$$x_{3}=frac{pi}{2}+pi*n, quad n in Z;$$
Помним, что нам еще как-то надо проверить, подходят ли получившиеся корни под ОДЗ. На старом рисунке отметим наши корни. Все точки, которые попадают в левую часть окружности, не удовлетворяют ОДЗ, а в правой части – удовлетворяют.
Ответ:
$$x_{1}=frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{2}=-frac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{3}=frac{pi}{2}+pi*n, quad n in Z;$$
Обратите внимание, что в ответе период стал (2pi*n), а не (pi*n), как у нас получалось при решении. Это связано с тем, что период (pi*n) покрывает на окружности две точки: из левой полуокружности, которая нам не подходит по ОДЗ, и из правой, которая подходит. А раз нам подходит только одна правая точка, то период будет (2pi*n).
Разные типы тригонометрических уравнений
Подведем важные итоги. Существует три основных метода решения тригонометрических уравнений: замена переменной, вынесение общего множителя (группировка), и деление (однородные уравнения).
Во избежание ошибок, я бы всегда стремился решать либо через замену, либо через вынесение общего множителя. А деление использовать, когда у вас не получается решить другими способами. Это убережет от ошибок, описанных в конце главы про однородные уравнения.
Порешаем разные полезные нестандартные уравнения, которые могут встретиться на ЕГЭ.
Пример 32
$$4cos^4(x)-4cos^2(x)+1=0;$$
Уравнение с четвертой степенью, но пугаться не надо. Это биквадратное уравнение, которое мы решим при помощи простой замены:
$$t=cos^2(x);$$
$$4t^2-4t+1=0;$$
Перед вами формула сокращенного умножения – полный квадрат:
$$(2t-1)^2=0;$$
$$t=frac{1}{2};$$
Обратная замена:
$$cos^2(x)=frac{1}{2};$$
Перед нами еще одно квадратное уравнение. Чтобы такое решить, перенесем все в левую часть и разложим по формуле разности квадратов:
$$cos^2(x)-frac{1}{2}=0;$$
$$(cos(x)-sqrt{frac{1}{2}})(cos(x)-sqrt{frac{1}{2}})=0;$$
Произведение равно нулю, когда один из множителей равен нулю. Первый множитель:
$$cos(x)-sqrt{frac{1}{2}}=0;$$
$$cos(x)=sqrt{frac{1}{2}};$$
$$cos(x)=frac{1}{sqrt{2}};$$
$$x_{1,2}=pmfrac{pi}{4}+2pi*n, quad n in Z;$$
Второй множитель:
$$cos(x)+sqrt{frac{1}{2}}=0;$$
$$cos(x)=-sqrt{frac{1}{2}};$$
$$cos(x)=-frac{1}{sqrt{2}};$$
$$x_{3,4}=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Ответ:
$$x_{1,2}=pmfrac{pi}{4}+2pi*n, quad n in Z;$$
$$x_{3,4}=pmfrac{3pi}{4}+2pi*n, quad n in Z;$$
Пример 33
$$sqrt{3}sin(2x)+3cos(2x)=0;$$
Обратите внимание, что тут обе тригонометрические функции берутся от (2x). В предыдущих примерах мы всегда избавлялись от (2x) и старались преобразовать так, чтоб аргумент был просто (x).
Но, оказывается, так делать необязательно. Так как тут аргумент везде (2x), то будем решать с ним. Нам, на самом деле, не важно, какой у вас аргумент, главное, чтобы он был одинаковый у всех тригонометрических функций, входящих в уравнение.
Разделим исходное уравнение на (cos(2x)), при этом убедимся, что (cos(2x)=0) не будет являться решением. Так как (sin(2x)) и (cos(2x)) одновременно при одинаковых значениях (x) не могут равняться нулю, то (cos(2x)=0) не является решением уравнения и можно спокойно делить:
$$sqrt{3}tg(2x)+3=0;$$
$$tg(2x)=frac{-3}{sqrt{3}};$$
$$tg(2x)=-sqrt{3};$$
$$2x=-frac{pi}{3}+pi*n, quad n in Z;$$
$$x=-frac{pi}{6}+frac{pi*n}{2}, quad n in Z;$$
Ответ:
$$x=-frac{pi}{6}+frac{pi*n}{2}, quad n in Z;$$
Как пользоваться формулами приведения? Правило лошади, единичная окружность и формулы суммы и разности для нахождения формул приведения.
Как пользоваться тригонометрической окружностью? Синус, косинус, тангнес и котангнес на единичной окружности. Свойства симметрии. Перевод градусов в радианы.
Разбираем тригонометрию с нуля. Синус, косинус, тангенс и котангенс в прямоугольном треугольнике. Таблица стандартных углов и свойства тригонометрических функций.
Как решать показательные неравенства. Общий алгоритм решения. Замена переменной. Однородные степенные неравенства.
Как решать неравенства с логарифмами. Общий алгоритм решения. Замена переменной. Переменное основание в логарифмических неравенствах. Сужение ОДЗ.
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Как решать уравнения со степенями. Разбираем основные методы и способы решения простейших показательных уравнений.
Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.
Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.
Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.
- Главная
- Учебники
- Алгебра, 11 класс
- ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
Алгоритм: Решение уравнений с ограничениями: .
-
Надо выписать ОДЗ — условия: условия существования выражений в уравнении. Решить получившиеся неравенства.
-
На тригонометрической окружности Е.Т.О. отметить области, промежутки точек, выполняющих условия ОДЗ.
-
Решить уравнение, отметить точки на Е.Т.О. , соответствующие полученным сериям решений.
-
Выбрать те точки, которые «попали» в допустимые промежутки, области. Какие числа-углы соответствуют этим точкам?
-
Написать серии для этих точек — эти серии и будут корнями нашего уравнения.
-
Выписать несколько конкретных корней. Перебрать разные $n$, $m$ целые числа, игнорируя заведомо не попадающие в ограничения.
-
Проверить каждый кандидат — корень: удовлетворяет ли условиям ограничения, входит ли в требуемый промежуток?
Задача 1: а) Решите уравнение $left(sin^2frac{x}{2}+frac{3cdot cos x}{2}right)left(sqrt{3}ctg x+1right)sqrt{-7sin x}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;-frac{pi}{2}right]$ .
- ОДЗ: под радикалом $-7sin xge0$ ; Условие на существование котангенса $xnepi n$ — тоже самое, что $sin xne0$;
- Итоговое ОДЗ: $sin x<0$ — корнями могуть быть углы из 3-ей и 4-ой четверти, в нижней части Е.Т.О окружности.
- Решаем уравнение: здесь произведение нескольких множителей равно 0. Значит, распад на случаи — каждый множитель = 0.
- Факт: «Произведение сравнить с нулем можно свести к сравнению с нулем каждого множителя»:
- Уравнение: $Acdot Bcdot C=0$ $Rightarrow$ I случай $A=0$ , II случай $B=0$ , III случай $C=0$
- Последнее $sqrt{-7sin x}=0$ незачем решать т.к. мы уже установили при ОДЗ, что $sin xne0$ из-за присутствия котангенса.
- I случай: $sin^2frac{x}{2}+frac{3cdot cos x}{2}=0$ .
- Какие здесь углы? $frac{x}{2}$ и $x$ . Значит, можем свести к одному углу!
- По формуле удвоенного угла $cos x=1-2sin^2frac{x}{2}$ сможем прийти к замене $y=sinfrac{x}{2}$. Но, решим по-другому …
- по формуле понижения степени — половинного угла: $frac{1-cos x}{2}+frac{3cdot cos x}{2}=0$ придем к простому
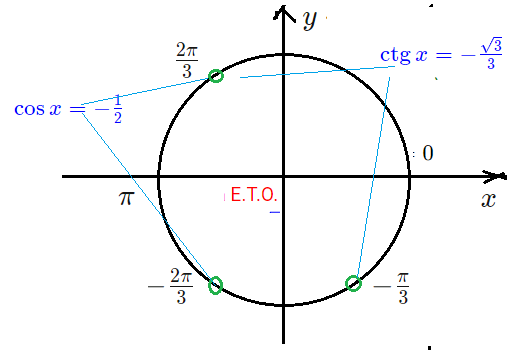
- $1+2cos x=0$ $Rightarrow$ $cos x=-frac{1}{2}$ его корни: $x=frac{2pi}{3}+2pi n$ $x=-frac{2pi}{3}+2pi m$
- Смотрим на Е.Т.О. — из этих двух точек-серий по ОДЗ нас устраивает только из 3-ей четверти: $x=-frac{2pi}{3}+2pi m$
- II случай: $sqrt{3}ctg x+1=0$ «если в уравнении лишь одна функция, ее следует выразить …»:
- $ctg x=-frac{sqrt{3}}{3}$ корни: 2 точки-серии $x=-frac{pi}{3}+pi k$. Устраивает по ОДЗ: $x=-frac{pi}{3}+2pi k$
- ответ a): $x=-frac{2pi}{3}+2pi m$ $x=-frac{pi}{3}+2pi k$ . (Две точки из нижней части Е.Т.О.).
- Пункт б): Ищем корни из требуемого промежутка $left[-4pi;-frac{pi}{2}right]$. Выпишем несколько возможных кандидатов для каждой серии:
- Из I серии: $-frac{2pi}{3}+2pi$, $-frac{2pi}{3}$, $-frac{2pi}{3}-2pi=-frac{8pi}{3}$, $-frac{2pi}{3}-4pi$. Входит: 2-ой и 3-ий.
- Из II серии: $-frac{pi}{3}+2pi$, $-frac{pi}{3}$, $-frac{pi}{3}-2pi=-frac{7pi}{3}$, $-frac{pi}{3}-4pi$. Попал лишь 3-ий.
- Требуемому ограничению удовлетворяют корни, ответ б): $-frac{2pi}{3}$, $-frac{7pi}{3}$, $-frac{8pi}{3}$,
Задача 2: а) Решите уравнение $frac{3cos^2 4x-7left(sin 4x+1right)}{sqrt{2sin x-1}}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;frac{2pi}{3}right]$ .
- ОДЗ — условия: знаменатель не ноль, под радикалом неотрицательно: $2sin x-1>0$
- Надо понять какие точки удовлетворяют ОДЗ на тригонометрической окружности Е.Т.О. Реши неравенство.
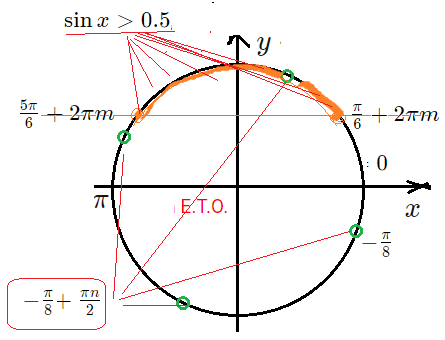
- Но пока уравнение: $2sin x-1=0$ $sin x=0.5$ $x=frac{pi}{6}+2pi m$ $x=frac{5pi}{6}+2pi m$
- Отметим эти точки-серии на Е.Т.О. Решение неравенства — это точки, в которых $sin x>0.5$ , значит точки с $y$ — координатой выше $>0.5$ .
- Значит, неравенство и ОДЗ выполняется в точках дуги , верхней части окружности между точками $frac{pi}{6}$ и $frac{5pi}{6}$.
- Теперь решаем само уравнение: «Дробь = 0 $Rightarrow$ числитель дроби = 0″. Алгоритм: $frac{A}{B}=0$ $Rightarrow$ $A=0$
- Итак: $3cos^24x-7left(sin4x+1right)=0$ У нас 2 функции, 1 аргумент. Выразим первую через вторую:
- $3cos^24x=1-sin^24x$ — Основное тождество, $3left(1-sin^24xright)-7left(sin4x+1right)=0$ .
- Упростим: $3sin^24x+7sin4x+4=0$ 1 функция, 1 аргумент — все готово к методу замены:
- замена $y=sin4x$ подстановка: $3y^2+7y+4=0$ корни: $y=-1$ $y=-frac{4}{3}$
- $y=-1$ возвратное: $sin4x=-1$ $Rightarrow$ $4x=-frac{pi}{2}+2pi n$ $Rightarrow$ $x=-frac{pi}{8}+frac{pi n}{2}$
- $y=-frac{4}{3}$ возвратное: $sin4x=-frac{4}{3}$ — нет решениий, т.к $-frac{4}{3}<-1$ , а синус не может стать меньше $<-1$
- Отметим серию $x=-frac{pi}{8}+frac{pi n}{2}$ — это точки, получающиеся от точки $-frac{pi}{8}$ прокруткой четверть оборотов $frac{pi}{2}$.
- Получаются четыре точки на Е.Т.О.: $-frac{pi}{8}$, $frac{3pi}{8}$, $7frac{pi}{8}$, $-5frac{pi}{8}$.
- Из этих 4-х точек в интервале ОДЗ $left(frac{pi}{6};frac{5pi}{6}right)$ находится только точка $frac{3pi}{8}$ .
- ОДЗ удволетворяют углы: $frac{3pi}{8}$ и его $2pi$ — прокуртки. ответ а): $frac{3pi}{8}+2pi n$
- Пункт б): Ищем корни из требуемого промежутка . Выпишем несколько возможных кандидатов из серии $frac{3pi}{8}+2pi n$:
- кандидаты: $frac{19pi}{8}$ $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$ $-frac{45pi}{8}$ . Какие из них попадают в интервал $left[-4pi;frac{2pi}{3}right]$
- Проверка принадлежности промежутку ограничения: ответ б): $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$,
Послесловие: Какие навыки, умения, смыслы, понятия надо знать?
- Е.Т.О — связь углов, точек на окружности, серии углов, прокрутки в пол-оборота, полный оборот, части.
- Формулы решения простейших тригонометрических уравнений, интерпретация в виде точек на Е.Т.О.
- Решение неравенств, изображение решений на Е.Т.О. Перевод точек на серии углов и наоборот.
- Анализ ОДЗ: радикалы, знаменатели, тангенс-котангенс. Анализ условий ограничений. Интерпретация на Е.Т.О.
- Методы решения тригонометрических уравнений: простейших, метод замены, разложение на множители, понижение степени, однородные.
Интерактивная Доска
Упражнения
- ЕГЭ по математике профиль
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
Связанные страницы:
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Перейти к содержанию
Подборка заданий для подготовки к ЕГЭ по биологии. Задания с рисунками.
На чтение 1 мин Просмотров 9 Опубликовано 12 марта, 2023
Подборка заданий для подготовки к ЕГЭ по биологии. Задания с рисунками. Решение и ответы на задачи на официальном сайте источника онлайн.
В КИМах по биологии достаточное количество заданий с рисунками. Работа с ними часто вызывает затруднения у выпускников. Надеюсь, подборка материала (с сайта «Решу ЕГЭ» и открытого банка заданий ФИПИ) поможет ученикам качественно поготовиться к итоговой аттестации.
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/biologiya/library/2016/09/03/podborka-zadaniy-dlya-podgotovki-k-ege-po-biologii-zadaniya-s
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
Положительное целое
шестизначное
нечетное
число 500917
– составное число.
Произведение всех цифр: 0.
У числа 8 делителей.
Обратным числом является 0.000001996338714797062.
Данное число представляется произведением: 23 * 29 * 751.
Системы счисления:
двоичная система: 1111010010010110101, троичная система: 221110010111, восьмеричная система: 1722265, шестнадцатеричная система: 7A4B5.
Число байт 500917 это 489 килобайтов 181 байт .
Кодирование азбукой Морзе: ….. —— —— —-. .—- —…
Число 500917 не является числом Фибоначчи.
Косинус числа 500917: -0.8659, синус числа 500917: 0.5002, тангенс числа 500917: -0.5777.
Логарифм натуральный числа 500917: 13.1242.
Логарифм десятичный числа 500917 равен 5.6998.
707.7549 — квадратный корень, 79.4185 — кубический.
Возведение числа в квадрат: 2.5092e+11.
Конвертация из числа секунд это 5 дней 19 часов 8 минут 37 секунд .
Нумерологическое значение числа 500917 – цифра 4.
Курс-помощник в подготовке к ЕГЭ по русскому языку. Позволяет детально разобрать задания формата ЕГЭ, но не направлен на монотонное прорабатывание вариантов. Для тех, кто хочет понимать, что происходит, и не надеется на удачу.
About this course
Это копия курса «Соточка по русскому» (ссылка), созданная для размещения в каталоге Stepik. Можно приобрести любой из курсов — внутри они совершенно одинаковые.
Перед вами курс «Соточка по русскому».
На курсе мы разбираем не отдельные задания ЕГЭ, а систему языка в целом, плавно подходя к заданиям формата ЕГЭ.
Это не значит, что курс содержит лишнюю информацию — нет, просто мы будем идти от простого к сложному, придерживаясь строгой логики. Так, например, начнём мы аж с грамматической основы.
Русский язык — больше не хаос, а прямая линия к цели.
Курс предназначен для подготовки к тестовой части ЕГЭ по русскому языку.
В курсе есть:
- теория, которая даётся СИСТЕМНО
- общий КОНСПЕКТ, который можно распечатать и учить (вся теория в одном файле)
- лёгкие задания на проверку усвоения теории;
- настоящие задания ЕГЭ прошлых лет
- система повторений (сложные случаи встретятся вам не раз и не два, это касается слов с ПРЕ/ПРИ, паронимов, слов с проблемным ударением и т.д.)
- ПРЕПОДАВАТЕЛЬ, который обязательно ответит на все вопросы в течение суток, но обычно это случается гораздо раньше
- дополнительный модуль с теорией по 27 заданию (СОЧИНЕНИЕ)
- дополнительный модуль с теорией по итоговому сочинению
ВНИМАНИЕ!
- У курса нет даты старта — вы можете начинать его прохождение в ЛЮБОЙ МОМЕНТ (так как теория дается в формате видео, которые уже записаны)
- Курс можно проходить сколько угодно: можно растянуть его на год, можно пройти за две недели, цена курса при этом не изменится. У нас нет подписок по месяцам: после покупки курс ваш навсегда.
- Курс — это система видео (от 2-х до 10-и минут), после которых нужно выполнить ряд заданий на закрепление материала. Так вы лучше усвоите информацию, чем при просмотре огромных вебинаров на курсах онлайн-школ.
- Теория в формате видео гарантирует отсутствие «воды» в материале. Время слишком ценно при подготовке, поверьте.
- На курсе более 2000 заданий, это и есть ваша «домашняя работа». Задания проверяются автоматически — не нужно будет ждать проверки преподавателем.
- Если вы чего-то не понимаете в материале — задавайте вопросы в комментариях, преподаватель отвечает на них каждый день: он приведёт более подробное объяснение, больше примеров — вы точно всё поймёте. Главное — не стесняться!
- Если вы всё-таки очень стесняетесь — ученики курса и преподаватель общаются между собой в беседе во Вконтакте (ссылка на беседу внутри курса). Здесь можно делиться всем, а не только обсуждать материал. Взаимная мотивация и дух товарищества не дадут вам забросить подготовку =)
На курсе 22 часа видео и более 2000 заданий (на их прохождение в среднем уходит 46 часов). То есть в целом прохождение курса занимает 68 часов.
Отзывы о курсе можно почитать здесь: ссылка
Последние обновления на курсе:
09.09.2022 — обновление блока, посвященного итоговому сочинению (2022-2023 учебный год)
15.09.2022 — обновление урока, посвященного 9-му заданию ЕГЭ
20.09.2022 — обновление цветного конспекта курса согласно демоверсии ЕГЭ 2023 года
22.09.2022 — обновление ч/б конспекта курса согласно демоверсии ЕГЭ 2023 года
2.10.2022 — добавление новых слов в порции слов с проблемным ударением
3.10.2022 — полностью обновлён модуль, посвященный сочинению ЕГЭ 2023 (включая конспект)
7.10.2022 — обновление урока, посвященного 3-му заданию ЕГЭ
7.10.2022 — добавление новых слов в порции паронимов
9.11.2022 — добавление урока, посвященного орфограммам О/Ё после шипящих, И/Ы после Ц в корне
24.11.2022 — добавление дополнительного урока, посвященного типам сказуемого (бонусный урок в блоке «Не для ЕГЭ»)
14.12.2022 — обновление урока, посвящённого теме «Приложение»
15.12.2022 — добавление дополнительного модуля, посвященного повторению паронимов (см. Бонусный модуль 2)
29.01.2023 — добавление урока «Однородные и неоднородные определения: закрепление»
07.02.2023 — обновление модуля, посвященного 14-му заданию
21.02.2023 — добавление урока «Обособление междометий»
КУРС ПОЛНОСТЬЮ СООТВЕТСТВУЕТ ФОРМАТУ ЕГЭ 2023
Whom this course is for
11-классники и все желающие сдавать ЕГЭ по русскому языку в 2023 году
Meet the Instructors
Course content
Certificate
Stepik certificate
Price
FAQ
Share this course
https://stepik.org/course/92015/promo






.png)























































































































































