Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 189 человек. Голоса между кандидатами распределились в отношении 2:7. Сколько голосов получил победитель?
Спрятать решение
Решение.
Найдём количество голосов в одной части:
Найдём количество человек проголосовавших за победителя:
Ответ: 147.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 153692.
Каталог заданий
Версия для печати и копирования в MS Word
1
Тип 15 № 506736
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 189 человек. Голоса между кандидатами распределились в отношении 2:7. Сколько голосов получил победитель?
Аналоги к заданию № 506736: 514610 514630 Все
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 153692.
Раздел кодификатора ФИПИ: Проценты, округление
Решение
·
·
Сообщить об ошибке · Помощь
Задания
Версия для печати и копирования в MS Word
Тип 2 № 506736
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 189 человек. Голоса между кандидатами распределились в отношении 2:7. Сколько голосов получил победитель?
Спрятать решение
Решение.
Найдём количество голосов в одной части:
Найдём количество человек проголосовавших за победителя:
Ответ: 147.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-11

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Тренировочный вариант №15 и вариант №16 в формате решу ЕГЭ 2023 по математике 11 класс профильный уровень от 10 января 2023 года с ответами и решением по новой демоверсии ЕГЭ 2023 года для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
- Скачать вариант №15 с ответами
- Скачать вариант №16 с ответами
- Скачать решение заданий варианта №15
- Скачать решение заданий варианта №16
ege2023-var15-prof
1. В треугольнике 𝐴𝐵𝐶 𝐴𝐶 = 𝐵𝐶, 𝐴𝐵 = 20, высота 𝐴𝐻 равна 8. Найдите синус угла 𝐵𝐴𝐶.
2. Дана правильная треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1, площадь основания которой равна 8, а боковое ребро равно 6. Найдите объём многогранника, вершинами которого являются точки 𝐴, 𝐶, 𝐴1, 𝐵1, 𝐶1.
3. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 3 сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
4. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
5. Найдите корень уравнения 7 −6−𝑥 = 343.
7. На рисунке изображён график 𝑦 = 𝑓 ′(𝑥) − производной функции 𝑓(𝑥). На оси абсцисс отмечены девять точек: 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5, 𝑥6, 𝑥7, 𝑥8, 𝑥9 . Сколько из этих точек лежит на промежутках убывания функции 𝑓(𝑥)?
8. Перед отправкой тепловоз издал гудок с частотой 𝑓0 = 192 Гц. Чуть позже гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка 𝑓 (в Гц) больше первого: она зависит от скорости тепловоза 𝜈 (в м/с) по закону 𝑓(𝜈) = 𝑓0 1− 𝜈 𝑐 (Гц), где 𝑐 — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 8 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 𝑐 = 300 м/с. Ответ дайте в м/с.
9. На изготовлении 60 деталей первый рабочий тратит на 4 часа меньше, чем второй рабочий на изготовление 80 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
13. В треугольной пирамиде 𝑆𝐴𝐵𝐶 известны боковые рёбра: 𝑆𝐴 = 𝑆𝐵 = 7, 𝑆𝐶 = 5. Основанием высоты этой пирамиды является середина медианы 𝐶𝑀 треугольника 𝐴𝐵𝐶. Эта высота равна 4. а) Докажите, что треугольник 𝐴𝐵𝐶 равнобедренный. б) Найдите объём пирамиды 𝑆𝐴𝐵𝐶.
15. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на 𝑟% по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите 𝑟.
18. Имеется 10 карточек. На них записывают по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11. После этого числа на каждой карточке складывают, а полученные десять сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Вариант №16 ЕГЭ 2023 профильный уровень
ege2023-var16-prof
1. В треугольнике 𝐴𝐵𝐶 угол 𝐶 равен 90°, 𝐵𝐶 = 6, 𝐴𝐵 = 10. Найдите sin 𝐵.
2. Площадь поверхности шара равна 12. Найдите площадь большого круга шара.
3. В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
4. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
5. Найдите корень уравнения 3 log9(4𝑥+1) = 9.
7. На рисунке изображён график 𝑦 = 𝑓 ′(𝑥) − производной функции 𝑓(𝑥), определённой на интервале (−11; 6). Найдите количество точек минимума функции 𝑓(𝑥), принадлежащих отрезку [−6; 4].
9. Два велосипедиста одновременно отправились в 160-километровый пробег. Первый ехал со скоростью, на 6 км/ч большей, чем скорость второго, и прибыл к финишу на 6 часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
10. На рисунке изображён график функции вида 𝑓(𝑥) = 𝑎 𝑥 . Найдите значение 𝑓(4).
11. Найдите точку минимума функции 𝑦 = (𝑥 2 − 17𝑥 + 17) ∙ 𝑒 7−𝑥 .
13. В основании четырёхугольной пирамиды 𝑆𝐴𝐵𝐶𝐷 лежит прямоугольник 𝐴𝐵𝐶𝐷 со сторонами 𝐴𝐵 = 8 и 𝐵𝐶 = 6. Длины боковых рёбер пирамиды 𝑆𝐴 = √21, 𝑆𝐵 = √85, 𝑆𝐷 = √57. а) Докажите, что 𝑆𝐴 − высота пирамиды. б) Найдите угол между прямыми 𝑆𝐶 и 𝐵𝐷.
15. В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы: – в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года; – в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года; – к июлю 2033 года кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?
16. К окружности, вписанной в квадрат 𝐴𝐵𝐶𝐷, проведена касательная, пересекающая стороны 𝐴𝐵 и 𝐴𝐷 в точках 𝑀 и 𝑁 соответственно. а) Докажите, что периметр треугольника 𝐴𝑀𝑁 равен стороне квадрата. б) Прямая 𝑀𝑁 пересекает прямую 𝐶𝐷 в точке 𝑃. В каком отношении делит сторону 𝐵𝐶 прямая, проходящая через точку 𝑃 и центр окружности, если 𝐴𝑀: 𝑀𝐵 = 1: 3?
17. Найдите все значения 𝑎, при каждом из которых уравнение ln(6𝑎 − 𝑥) ln(2𝑥 + 2𝑎 − 2) = ln(6𝑎 − 𝑥) ln(𝑥 − 𝑎) имеет ровно один корень на отрезке [0; 1].
18. На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Среднее арифметическое написанных чисел равнялось 7. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 1, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 14?
б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13?
в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
- Статград математика 11 класс ЕГЭ 2023 варианты и ответы
- Варианты статград МА2210209-МА2210212 и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Эта статья посвящена задачам из реального экзамена ЕГЭ по информатике 2022, которые были в этом году.
Посмотрим на сколько новый видеокурс по подготовке к ЕГЭ по информатике покрывает задачи из реального экзамена, а так же соответсвует последним веяньям моды.
Все задачи взяты с сайта: https://kompege.ru/variant?kim=25012688
Разбор задач с 19 по 27 задание.
Задание 1
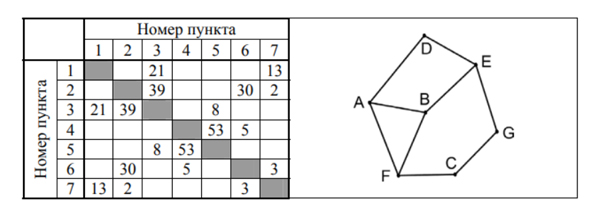
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта A в пункт D и из пункта G в пункта С. В ответе запишите целое число.
Решение:
Легко найти пункты G и С. Это две двойные точки и они связаны друг с другом. Получаем номера 4 и 5 (Здесь порядок может быть наооборот). Значит, мы знаем расстояние между G и С, оно равно 53.
Найдём точку В, она тройная и связана с тремя тройными точками. Это точка 2. От этой точки пойдём и найдём две тройные, связанные между собой. Это точки 6 и 7. Значит, это буквы A и Б (порядок может быть другим). Посмотрим, кто из них связан с точкой 4 или 5. Это точка 6. Значит точка 6 — это F. Точка 7 — это A. Седьмая точка связана с двойной точкой D. Точка D получается 1. Расстояние между семёркой и единицей равно 13.
Ответ получается 53 + 13 = 66.
Ответ: 66
Задание 2
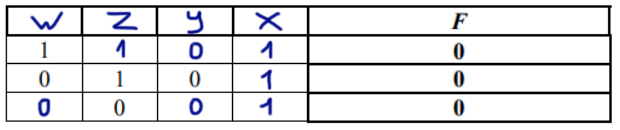
Миша заполнял таблицу истинности логической функции F
¬(w → z) ∨ (x → y) ∨ ¬x
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
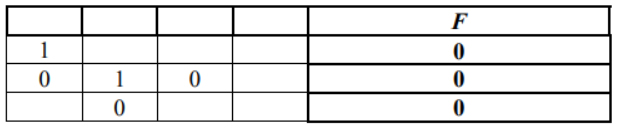
Пример. Функция F задана выражением ¬x / y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Напишем шаблон, о котором было рассказано в видеокурсе по подготовке к ЕГЭ по информатике.
print('x', 'y', 'z', 'w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( not((not(w) or z)) or (not(x) or y) or not(x) ): print(x, y, z, w)
Получается такая таблица истинности:
x y z w
1 0 0 0
1 0 1 0
1 0 1 1
Каждый столбец имеет хотя бы один ноль, кроме последнего, поэтому последний столбец уходит переменной x, там все единицы.
Тогда все нули идут в предпоследний столбец, там будет переменная y.
У нас есть срочка с тремя нулями и одной единицей. Это может быть только последняя строчка, т.к. в первых двух строчках уже по две единицы. Значит, в первом столбце в последней ячейке ставим ноль. Получается w идёт в первый столбец, а переменная z во второй.
Ответ: wzyx
Задание 3
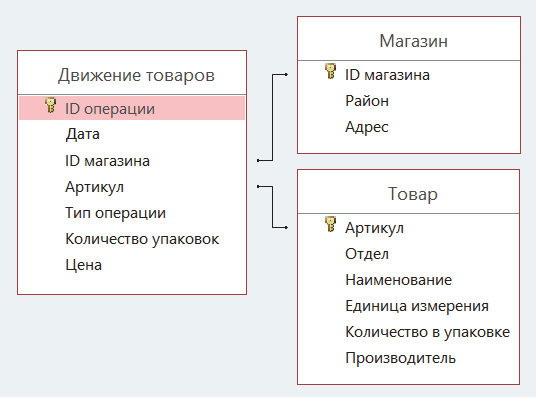
В файле приведён фрагмент базы данных «Продукты» о поставках товаров
в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию
о проданных товарах. Поле Тип операции содержит значение Поступление
или Продажа, а в соответствующее поле Количество упаковок, шт.
занесена информация о том, сколько упаковок товара поступило в магазин
или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции |
Дата | ID магазина |
Артикул | Тип операции |
Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках
каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. |
Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов.
Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, опредилите, на сколько увеличилось количество упаковок всех видов макарон производителя «Макаронная фабрика», имеющихся в наличии в магазинах Первомайского района, за период с 1 по 8 июня включительно.
В ответе запишите только число.
Решение:
Найдём артиклы всех макаронных изделий «Макаронной фабрики».
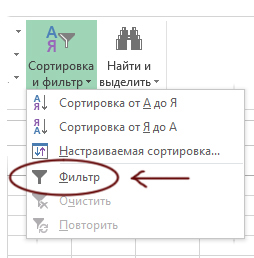
Открываем вкладку «Товар», кликаем в ячейку F1, выбираем кнопку на вкалдке «Главная» -> Сортировка и фильтр -> Фильтр.
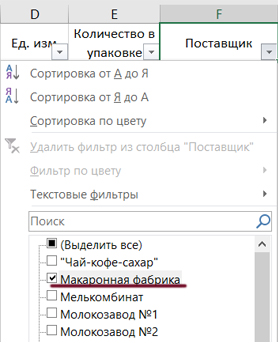
Кнопка Фильтр может находится и на главной панеле. Теперь можно отфильровать товары только «Макаронной фабрики».
Получаются номера артиклов: 24, 25, 26, 27.
Аналогично отфильтровываем магазины Первомайского района. Получаются номера ID: M2, M4, M7, M8, M12, M13, M16.
После этого, переходим на вкладку «Движение товаров». Так же включаем фильтры и оставляем только нужные артиклы макаронных изделий и нужные ID магазинов.
Если мы ещё отфильтруем товары по типу «поступления», мы узнаем сколько макаронных изделий пришло в нужные нам магазины. После фильтрации остаётся только первое июня, значит, про дату пока не нужно думать.
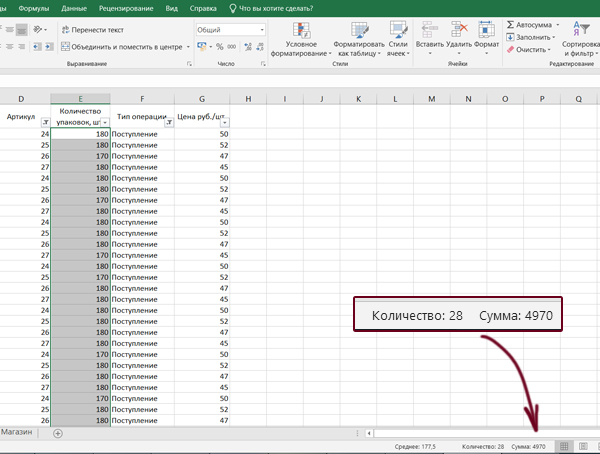
Выделяем ячейки столбца Количество упаковок и внизу смотрим сумму этих ячеек. Получается 4970 упаковок.
Здесь нельзя пользоваться стандартной функцией СУММ, потому что она суммируем ещё и скрытые ячейки. А так мы получаем сумму выделенных ячеек.
Аналогично находим, сколько товаров было продано. В столбце «Тип операции» отфильтровываем по типу «Продажа».
Дата опять осталась только одна (1 июня). Получается, продали 3360 упаковок.
Следовательно, увеличилось на 4970 — 3360 = 1610 упаковок всех макаронных изделий в указанных магазинах за период с 1 по 8 июня включительно.
Ответ: 1610
Задание 4
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н — 1111, З — 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков постребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков.
Решение:
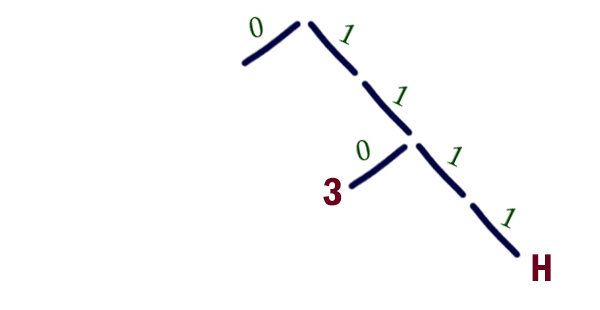
Расположим уже известные буквы на дереве Фано.
У нас остались три свободных места, если не продливать дерево: 0, 10, 1110.
Буква А встречается в слове КАЗАЧКА аж 3 раза. Значит, букве А присвоим код 0. Буква К встречается один раз, значит, ей код присвоим чуть побольше 10. Букве Ч достаётся код 1110. Это самый оптимальный способ распределить коды между оставшимися буквами.
Всего минимальная длина закодированного слова будет: 2 (К) + 1 (А) + 3 (З) + 1 (А) + 4 (Ч) + 2 (К) + 1 (А) = 14.
Ответ: 14
Задание 5
На вход алгоритма подаётся натуральное число N.
Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
a) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее, чем 16.
В ответе запишите это число в десятичной системе счисления.
Решение:
for n in range(1, 1000): s=format(n, 'b') if s.count('1')%2==0: s = s + '0' s = '10' + s[2:] else: s = s + '1' s = '11' + s[2:] r=int(s, 2) if r>=16: print(n)
Здесь мы пишем программу, как было написано в уроке видеокурса ЕГЭ по информатике. Но, действительно, встречается и новый приём. Нужно изменить левые символы нашей строки s. Это можно сделать с помощью такой конструкции s[2:]. Таким образом, мы берём всю строку, кроме двух первых символов. Например, s=’football’, то s[2:] будет обозначать ‘otball’.
Повторим основные идеи такого подхода при решении пятого задания из ЕГЭ по информатике с помощью программирования. Перебираем числа от 1 до 999 с помощью цикла for. В этом диапазоне надеямся найти наш ответ. С помощью команды format() превращаем число в строку уже в двоичной системе. Сумма цифр в строке зависит только от количества единиц. Нули ничего не дают в сумму. Поэтому применяем функцию .count. Дальше всё делаем, как написано в условии задачи. Команда int(s, 2) превращает строку в двоичной системе в число опять в десятичной системе счисления.
Ответ: 8
Задание 6
Определите, при каком наименьшем введённом значении переменной s программа выведет число 8. Для Вашего удобства программа представлена на четырёх языках.
*На данном сайте программа будет приведена на двух языках.
Решение:
Решать будем привычным способом — перебором. Здесь не нужно задействовать дополнительных особенных приёмов.
for i in range(-1000, 1000): s=i s = (s - 21) // 10 n = 1 while s>= 0: n = n * 2 s = s - n if n==8: print(i)
Ответ: 81
Задание 7
Для хранения сжатого произвольного растрового изображения размером 640 на 256 пикселей отведено 170 Кб памяти без учёта размера заголовка файла. Файл оригинального изображения больше сжатого на 35%. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении ?
Решение:
Пусть i — это количество бит в одном пикселе. Тогда i * 640 * 256 = 170Кб * 1,35. Находим i.
i = 170Кб * 1,35 / (640 * 256) = 11,475 бит.
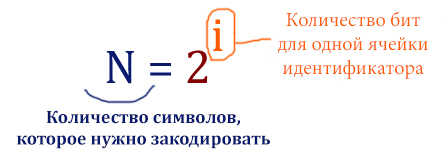
Здесь округляем в меньшую сторону, потому что, если округлим в большую сторону не уместимся в 170 кб. Далее действуем по формуле:
N = 2 i = 2 11 = 2048 цветов.
Ответ: 2048
Задание 8
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.
Решение:
Решим с помощью программы. Об этом мы говорили в видеокурсе ЕГЭ по информатике.
k=0 for x1 in '1234567': for x2 in '01234567': for x3 in '01234567': for x4 in '01234567': for x5 in '01234567': s = x1 + x2 + x3 + x4 + x5 if s.count('6')==1: if s.count('16')==0 and s.count('61')==0 and s.count('36')==0 and s.count('63')==0 and s.count('56')==0 and s.count('65')==0 and s.count('76')==0 and s.count('67')==0: k=k+1 print(k)
Ответ: 2961
Задание 9
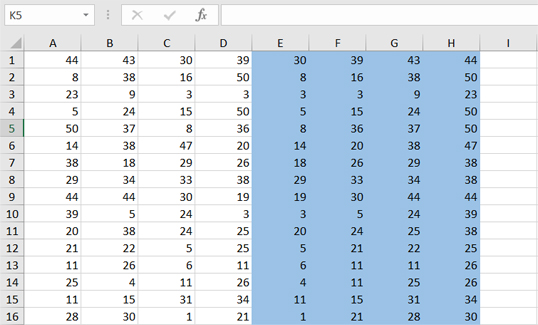
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа.
Определите количество строк таблицы, содержащих числа, для которых выполнены два условия:
— наибольшее из четырёх чисел меньше суммы трёх других;
— четыре числа можно разбить на две пары чисел с равными суммами.
В ответе запишите только число.
Решение:
В столбцах E, F, G, H мы хотим видеть отсортированные числа из нашей строки. Для этого воспользуемся функцией НАИМЕНЬШИЙ().
В ячейку E1 напишем формулу =НАИМЕНЬШИЙ(A1:D1; 1). В начале пишем диапазон, где мы рассматриваем числа, второй аргумент говорит, что мы хотим выбрать самый маленький элемент. Для ячейки F1 пишем =НАИМЕНЬШИЙ(A1:D1; 2). Т.e. выбираем второй по минимальности элемент. И так далее делаем для четырёх чисел.
Распространяем новые столбцы на всё пространство (как это делать, можете посмотреть в видеоуроке по 9 заданию в видеокурсе). Так же можно подсветить каким-нибудь цветом новые столбцы.
Здесь достаточно проверить одну комбинацию: максимальное число + минимальное число = сумма двух средних чисел. По другому нельзя получить одинаковые суммы пар чисел, если все числа не одинаковые в четвёрке. Но у нас нет такой строчки, где все четыре числа одинаковых (это можно отдельно проверить с помощью команды ЕСЛИ).
В столбце I расставим единицы напротив тех строчек, которые подходят под условие задачи, иначе, поставим 0. В ячейке I1 напишем формулу:
=ЕСЛИ(И(H1 < E1 + F1 + G1; E1 + H1 = F1 + G1); 1; 0)
Затем распространяем эту формулу на весь столбец и подсчитаем количество единиц в этом столбце.
Получается 104 строчки.
Ответ: 104
Задание 10
Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «солдаты» со строчной буквы. Другие формы этого слова учитывать не следует. В ответе запишите только число.
Решение:
Открываем соответствующий файл в программе Word. На вкладке «Главная» находится кнопка «Найти«. Кликаем по чёрному треугольнику возле этой кнопки и выбираем «Расширенный поиск«.
На вкладке «Главная» находится кнопка «Найти«. Кликаем по чёрному треугольнику возле этой кнопки и выбираем «Расширенный поиск«.
Далее, нажимаем кнопку «Больше>>«.
Теперь у нас есть все инструменты, чтобы решить 10 задание из ЕГЭ по информатике 2022.
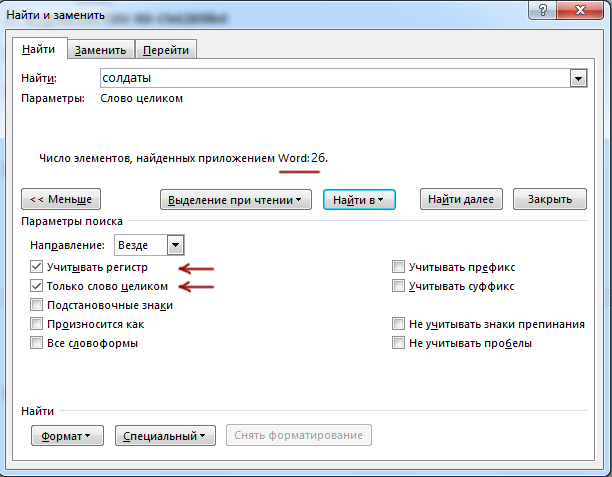
В поле «Найти» пишем наше слово «солдаты«. Галочку «Учитывать регистр» ставим, т.к. слово может быть только с маленькой буквы. Ставим галочку «Только слово целом«.
Нажимаем Найти в -> «Основной документ».
Получаем ответ 1.
Ответы: 26
Задание 11
При регистрации в компьютерной системе каждому объекту присваиватся идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого индетификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число — количество Кбайт.
Решение:
Воспользуемся формулой для 11-ого задания из ЕГЭ по информатике.
Вместо N подставляем число 1700 + 10 = 1710 (1700 символов плюс 10 цифр). Тогда
1710 < 211
Т.е. 11 бит точно хватит, чтобы закодировать 1710 символов.
В идетификаторе всего 252 ячейки. Найдём сколько будет «весить» один идетификатор: 252 * 11 = 2772 бит. Узнаем, сколько байт потребуется для одного идентификатора 2772 / 8 = 347 байт (округлили в большую сторону, чтобы точно хватило).
У нас всего 4096 идетификаторов. Тогда нам потребуется 4096 * 347 = 1421312 байт. Переведём в Кб: 1421312 / 1024 = 1388 Кб.
Ответ: 1388
Задание 12
Исполнитель Редактор получает на вход строку цифр и преобразовывает её.
Редактор может выполнять две команды, в обеих командах v и w обозначают
цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на
цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя
Редактор. Если она встречается, то команда возвращает логическое значение
«истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие
ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 96 идущих подряд цифр 9? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось(22222) ИЛИ нашлось(9999)
ЕСЛИ нашлось(22222) ТО заменить(22222, 99)
ИНАЧЕ заменить(9999, 2)
КОНЕЦ ЕСЛИ
КОЕНЦ ПОКА
КОНЕЦ
Решение:
Решать будем, как было показано в видеокурсе.
s='9'*96 while '22222' in s or '9999' in s: if '22222' in s: s = s.replace('22222', '99', 1) else: s = s.replace('9999', '2', 1) print(s)
Ответ: 299
Задание 13
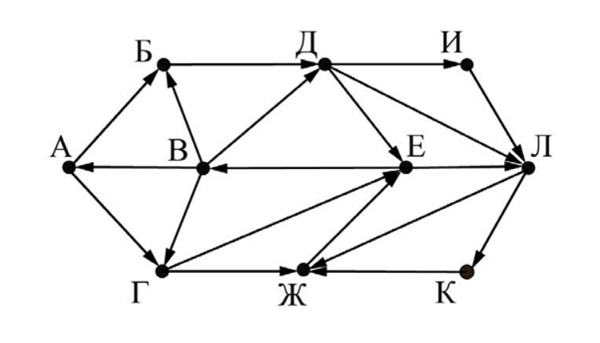
На рисунке представлена схема дороог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Решение:
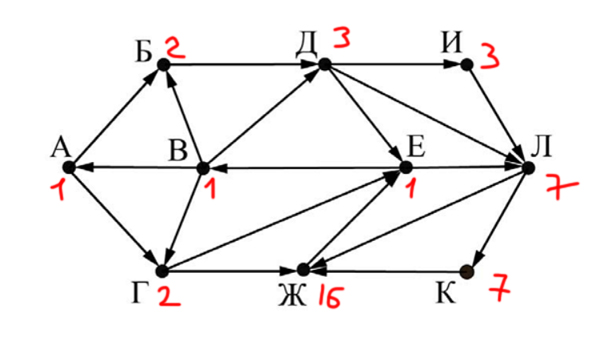
Решать будем примерно так же, как и классическую задачу. Основные идеи ни чем не отличаются.
В город Е входят города с числами: 16, 2 и 3. Значит, ответ получается 16 + 2 + 3 = 21.
Ответ: 21
Задание 14
Значение арифметического выражения
4*6251920 + 4*1251930 — 4*251940 — 3*51950 — 1960
записали в системе счисления с основанием 5. Определите количество значащих нулей в записи этого числа.
Решение:
Решаем классическим способом с помощью программирования.
f=4*625**1920 + 4*125**1930 - 4*25**1940 - 3*5**1950 - 1960 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('0'))
Ответ: 1891
Задание 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A >= 80)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x ?
Решение:
Применим шаблон из видокурса ЕГЭ по информатике.
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 10000): if (not(D(x, 2)) or not(D(x, 3))) or (x + A >= 80): k=k+1 if k==9999: print(A)
Здесь в начале пишем функцию D, которая олицетворяет функцию ДЕЛ. Потом перебираем различные натуральные значения A. Если функция для какого-то значения сработает 9999 раз, то будем считать, что такое значение A нам подходит.
Самое маленькое значение получается 74.
Ответ: 74
Задание 16
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 1 при n < 3;
F(n) = F(n — 1) + n — 1, если n>2 и при этом n чётное;
F(n) = F(n — 2) + 2n — 2, если n>2 и при этом n нечётное.
Чему равно значение функции F(34) ?
Решение:
Здесь достаточно просто запрограммировать этот алгоритм.
def F(n): if n<3: return 1 if n>2 and n%2==0: return F(n-1) + n - 1 if n>2 and n%2!=0: return F(n-2) + 2*n - 2 print(F(34))
Ответ: 578
Задание 17
В файле содержится последовательность натуральных чисел. Элементы последовательности могут принимать целые значения от 1 до 100 000 включительно. Определите количество пар последовательности, в которых остаток от деления хотя бы одного из элементов на 117 равен минимальному элементу последовательности. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумивается два идущих подряд элемента последовательности.
Решение:
В начале найдём самый маленький элемент последовательности.
f=open('17.txt') mn=10**9 for s in f.readlines(): x = int(s) mn=min(mn, x) print(mn)
Получается минимальное число равно 8.
f=open('17.txt') k=0 mx=0 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if n1%117==8 or n2%117==8: k=k+1 mx = max(mx, n1+n2) n1=n2 print(k, mx)
Ответ:
Задание 18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел
Решение:
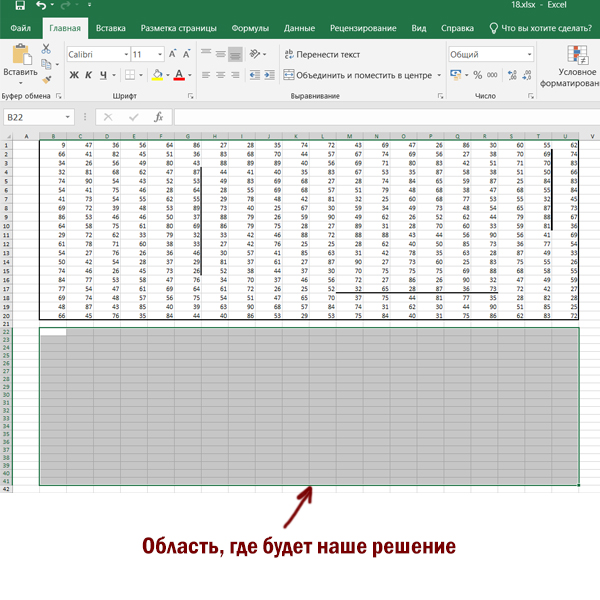
Открываем файл в программе Excel.
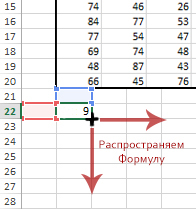
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
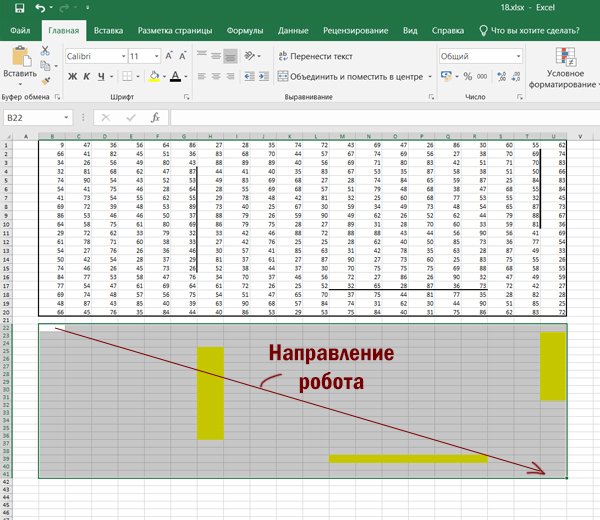
Распространим формулу на всё пространство, не трогая закрашенные клетки.
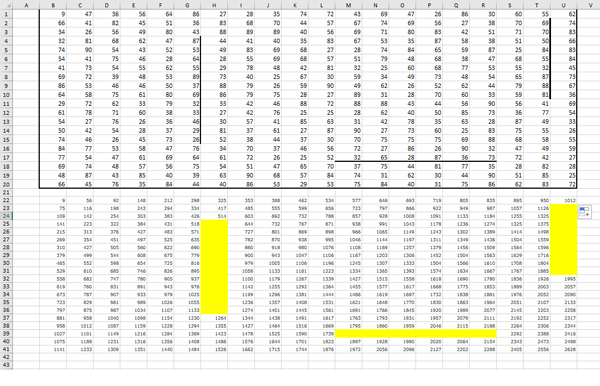
Получается такая картина:
В ячейки для первой закрашенной области, Робот может попасть только сверху! Поэтому пишем формулу для ячейки H25:
=H24+H4
Распространяем формулу по всему закрашенному столбцу.
В ячейки для второй закрашенной области, Робот может попасть только слева! Поэтому пишем формулу для ячейки М39:
=L39+M18
Распространяем формулу по всей закрашенной строчке.
В ячейке U23 напишем формулу:
=U22+U2
И тоже распространим формулу на закрашенную часть.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 2628.
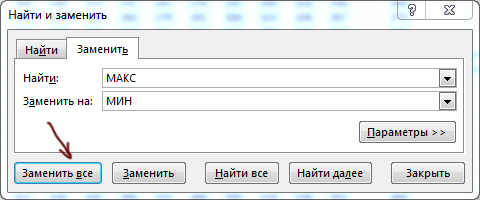
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 1659.
Ответ:
Разбор задач с 19 по 27 задание.
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html