Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила сумма, уплаченная Сергеем банку сверх кредита?
Спрятать решение
Решение.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму, без учета процентов, возвращал равными долями.
Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.
В первом месяце эта часть заплаченной суммы составляла во втором —
в третьем —
в восьмом —
наконец, в последнем —
Всего за 9 месяцев:
Искомое процентное отношение есть 60
Ответ: 60.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник: Интеллект-центр. Репетиционные варианты ЕГЭ 2015.
№1. Задание 19 № 507890. Оля хочет взять в кредит 100 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 24000 рублей?
Решение.
Пусть сумма кредита равна S, а годовые составляют a %. Тогда в последний день каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a Составим таблицу выплат.
|
Год |
Долг банку (руб.) |
Остаток доли после выплаты (руб.) |
|
0 |
100000 |
– |
|
1 |
110000 |
86000 |
|
2 |
94600 |
70600 |
|
3 |
77660 |
53660 |
|
4 |
59026 |
35026 |
|
5 |
38528,6 |
14528,6 |
|
6 |
15981,46 |
0 |
Значит, Оля погасит кредит за 6 лет.
Ответ: 6.
№2. Задание 19 № 507212. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Пусть сумма кредита равна а годовые составляют
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент
После первой выплаты сумма долга составит
После второй выплаты сумма долга составит
После третьей выплаты сумма оставшегося долга равна
После четвертой выплаты сумма оставшегося долга равна
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
При и
получаем:
и
Ответ: 2 296 350.
ВТОРОЙ СПОСОБ
Пусть x — один из четырех разовых (равных) платежей.Тогда можно составить линейное уравнение:
(((((((6902000 * 1,125 ) – x ) * 1,125 ) – x ) * 1,125) – x ) * 1,125 ) –x = 0.
Выполнив все вычисления, получим:
11055669, 43359375 = 4,814453125x
x = 11055669,43359375/4,814453125
x = 2296350
Ответ: 2296350.
№3.Задание 19 № 506956. Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?
Решение.
Первый способ (близкий к арифметическому решению).
Пусть первый брокер купил акций, а второй —
акций. Тогда первый продал
акций, второй —
акций.
То, что сумма от продажи акций, полученных вторым брокером, на 140% превысила сумму, полученную первым брокером, означает: сумма, полученная вторым брокером, больше суммы, полученной первым, в 2,4 раза:
Так как цена одной акции у обоих брокеров одинакова, а полученные суммы прямо пропорциональны количеству акций, проданных каждым брокером, то
Если — коэффициент пропорциональности количества акций, купленных брокерами, то ими приобретено
акций на сумму 3640 р. Следовательно, на тот момент цена каждой акции составляла:
р.
Первый брокер продал акций, второй
акций. Всего было продано
акций. К моменту продажи цена одной акции стала
(р), т.е. на (р) выше.
Значит, цена одной акции возросла на 37,5%
Второй способ (преобладает алгебраический подход).
Пусть р. — первоначальная цена одной акции,
— количество акций, купленных первым брокером,
— количество акций, купленных вторым брокером. И пусть цена одной акции возросла на
%. Тогда: (1)
Со временем цена одной акции выросла до рублей.
Первый брокер продал акций на сумму рублей, а второй брокер — на рублей.
Согласно условию задачи имеем: т.е.
(2)
Так как сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером, то
Подставив полученное значение в уравнение (1), будем иметь:
Подставим то же значение в уравнение (2):
А значение нами найдено выше.
Следовательно,
Ответ: 37,5.
№4.Задание 19 № 506090. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение.
Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1 + 0,01k. После первой выплаты сумма долга составит: a1 = am − x. После второй выплаты сумма долга составит:
После третьей выплаты сумма оставшегося долга:
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому откуда При a = 9 930 000 и k = 10, получаем: m = 1,1 и
Ответ: 3 993 000 рублей.
Второй способ
Пусть — один из трёх разовых платежей. Тогда сумма долга после оплаты в первом году составит: После внесения второго платежа сумма долга станет равной Сумма долга после третьего платежа: Третьим платежом Сергей должен погасить долг, то есть долг станет равным нулю:
Третий способ
В первый год ему начислят 993000 и сумма долга составит 10923000 минус ежегодный платеж (х) и получаем следующее 10923000-х
На второй год опять проценты и минус ежегодный платеж:
(10923000-х)*1,1-х
На третий год та же история:
((10923000-х)*1,1-х)*1,1-х=0 (так как он закрыл долг тремя равными платежами).
Дальше нехитрые вычисления уровня средней школы и приходим к выражению:
3,31х=13216830
Отсюда находим, что х=3993000.
№ 5. Задание 19 № 506950. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?
Решение.
Общая сумма, причитающаяся вкладчику, включая дополнительные вклады в течение четырех лет и все процентные начисления, к концу пятого года хранения денег составляет 825 (100+725) процентов от первоначального (3900 тыс. руб.). Эта сумма равна:
(тыс.руб.)
Некоторая часть найденной суммы образована хранением первоначально вложенной суммы (3900 тыс.руб.) Вычислим эту часть. Поскольку процентная надбавка начислялась в размере 50% годовых, то за 5 лет хранения этой части вклада вложенная сумма увеличилась в раза. То есть стала:
(тыс. руб.)
Теперь найдем другую часть образованной суммы с учетом дополнительных вкладов в течение четырех лет, а также процентных начислений на эту сумму. Эта часть равна разности двух сумм, вычисленных выше.
(тыс. руб.)
Это — с одной стороны. С другой же стороны эта сумма образовалась так:
Пусть вкладчик в конце года и в течение 4 лет вносил дополнительный вклад в сумме тыс. руб.
В конце первого года хранения этой суммы она выросла до тыс. руб.
Вкладчик дополнительно внес еще тыс. руб. На начало следующего календарного года эта часть суммы стала:
(тыс.руб.)
Через год эта сумма выросла до:
(тыс.руб.)
Но вкладчик внес на счет еще тыс.руб. Сумма стала:
(тыс. руб.)
Через год эта сумма выросла до:
(тыс. руб.)
Вкладчик вновь внес на счет тыс. руб. Часть вклада становится равной:
(тыс.руб.)
К концу последнего года хранения всего вклада эта часть вырастает до:
(тыс. руб.)
Теперь решим уравнение:
Итак, искомая сумма равна 210 тыс. руб.
Ответ: 210 000.
№6.Задание 19 № 506948. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на Определите срок хранения вклада.
Решение.
Известно:
1. Проценты на вклад начислялись ежемесячно.
2. Каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.
Если первоначальная сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась месяцев, то вклад ежемесячно увеличивался в раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.
При изменении процентной надбавки с 5% на 12% (ставка 12% продержалась месяцев) первоначальная сумма вклада за
месяцев увеличится в раз.
Предположим, что процентная ставка продержалась
месяцев, а процентная ставка
продержалась
месяцев. Тогда соответствующие коэффициенты повышения составят:
и
Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке составит:
Это — с одной стороны. Но с другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на т.е. в
( раз).
Значит,
Согласно основной теореме арифметики каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования. В таком случае:
Решим эту систему относительно натуральных и
Из последнего уравнения системы имеем: При этих значениях
и
система примет вид:
Итак, вклад в банке на хранении был 7 месяцев. При найденных значениях и
действительно равно нулю.
Ответ: 7.
№7.Задание 19 № 506954. В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объема закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив ее на закупку нефти?
Решение.
Пусть сумма, которой первоначально располагала администрация края, составляла у.е., а цена барреля сырой нефти
у.е. Тогда первоначально возможный объем закупок составлял
баррелей. Этот объем примем за 100 процентов. За 2 месяца хранения в банке положенная сумм выросла до
у.е., а цена барреля сырой нефти за это же время убыла до у.е. Следовательно, 1 ноября 2001 г. руководство края на эту сумму могла закупить баррелей сырой нефти. Процентное отношение этого объема к первоначально возможному объему закупок составит:
% то есть % =
%.
Значит, руководство края смогло пополнить 1 ноября 2001 г. нефтяные запасы края на 96% больше, чем 1 сентября того же года.
Ответ: 96.
№8.Задание 19 № 506957. Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?
Решение.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму возвращал равными долями.
Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.
В первом месяце эта часть заплаченной суммы составляла , во втором — в третьем — в восьмом — наконец, в последнем —
Всего за 9 месяцев:
Искомое процентное отношение есть 60
Ответ: 60.
№9.Задание 19 № 507913. Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?
Решение.
Пусть сумма кредита равна S, а годовые составляют a %. Тогда в последний день каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a Составим таблицу выплат.
|
Год |
Долг банку (руб.) |
Остаток доли после выплаты (руб.) |
|
0 |
1200000 |
– |
|
1 |
1320000 |
1000000 |
|
2 |
1100000 |
780000 |
|
3 |
858000 |
538000 |
|
4 |
591800 |
271800 |
|
5 |
298980 |
0 |
Значит, Оля погасит кредит за 5 лет.
Ответ: 5.
Задание 19 № 506955. Транcнациональная компания Amako inc. решила провести недружественное поглощение компании First Aluminum Company (FAC) путем скупки акций миноритарных акционеров. Известно, что Amako inc. было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3, а общее количество приобретенных Amako inc. акций поглощаемой компании увеличивалась на 20%. Определите величину третьего предложения и общее количество скупленных акций First Aluminum Company, если начальное предложение составляло $27 за одну акцию, а количество акций, выкупленных по второй цене, 15 тысяч.
Решение.
|
Предложения |
Цена одной акции ($) |
Количество выкупленных акций |
|
|
При данном предложении |
Общее количество |
||
|
1 |
27 |
75000 |
75000 |
|
2 |
36 |
15000 |
90000 |
|
3 |
48 |
Для получения ответа вычисление не требуется |
108000 |
Ответ: третье предложение по цене $48 за одну акцию; общее количество выкупленных акций 108000.
№ 10.Задание 19 № 506951. Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Банк увеличил процент годовых на 40%. К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?
Решение.
Пусть банк первоначально вклад в размере у.е. принял под
годовых. Тогда к началу второго года сумма стала у.е.
После снятия четверти накопленной суммы на счету осталось у.е.
С момента увеличения банком процентной ставки на 40% к концу второго года хранения остатка вклада накопленная сумма стала
у.е.
По условию задачи эта сумма равна у.е.
Решим уравнение
;
Этот корень не подходит по смыслу задачи: Новые годовые составляют 20 + 40 = 60 %.
Ответ: 60.
№ 11.Задание 19 № 506958. Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Решение.
Пусть сумма кредита у.е., процентная ставка банка
%.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет:
(у.е.)
Общая сумма, выплаченная Антоном за 6 месяцев: (у.е.). А эта сумма по условию задачи равна у.е. Решим уравнение:
Ответ: 18.
№12.Задание 19 № 506953. В январе 2000 года ставка по депозитам в банке «Возрождение» составила х % годовых, тогда как в январе 2001 года — у % годовых, причем известно, что x + y = 30%. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной.
Решение.
Через лет на первом счёте будет сумма
В это же время на втором счёте будет сумма
Приравняем эти суммы и решим полученное уравнение:
Таким образом, суммы на счетах сравняются через 12 лет после открытия первого вклада.
Ответ: 12.
7
№1. Задание
17 № 507890. Оля хочет взять в кредит
100 000 рублей. Погашение кредита происходит раз в год равными суммами
(кроме, может быть, последней) после начисления процентов. Ставка процента
10 % годовых. На какое минимальное количество лет может Оля взять кредит,
чтобы ежегодные выплаты были не более 24000 рублей?
Решение.
Пусть сумма кредита
равна S, а годовые составляют a %. Тогда в последний
день каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a Составим
таблицу выплат.
|
Год |
Долг банку (руб.) |
Остаток доли после выплаты (руб.) |
|
0 |
100000 |
– |
|
1 |
110000 |
86000 |
|
2 |
94600 |
70600 |
|
3 |
77660 |
53660 |
|
4 |
59026 |
35026 |
|
5 |
38528,6 |
14528,6 |
|
6 |
15981,46 |
0 |
Значит, Оля погасит
кредит за 6 лет.
Ответ: 6.
№2.
Задание 17 № 507212. 31 декабря 2014 года
Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты
кредита следующая — 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на
12,5%), затем Алексей переводит в банк X рублей. Какой
должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными
платежами (то есть за четыре года)?
Решение.
Пусть сумма кредита
равна а
годовые составляют Тогда
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент После
первой выплаты сумма долга составит После
второй выплаты сумма долга составит
После третьей выплаты
сумма оставшегося долга равна
После четвертой выплаты
сумма оставшегося долга равна
По условию четырьмя
выплатами Алексей должен погасить кредит полностью, поэтому
При и
получаем:
и
Ответ: 2
296 350.
ВТОРОЙ СПОСОБ
Пусть x — один из четырех разовых (равных) платежей.Тогда
можно составить линейное уравнение:
(((((((6902000 * 1,125 ) – x ) * 1,125 ) –
x ) * 1,125) – x ) * 1,125 ) –x = 0.
Выполнив все вычисления, получим:
11055669, 43359375 = 4,814453125x
x = 11055669,43359375/4,814453125
x = 2296350
Ответ: 2296350.
№3.Задание 17 № 506956. Два брокера купили акции одного достоинства на сумму
3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму
3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом
сумма от продажи акций, полученная вторым брокером, на 140% превысила
сумму, полученную первым брокером. На сколько процентов возросла
цена одной акции?
Решение.
Первый способ (близкий
к арифметическому решению).
Пусть первый брокер
купил акций,
а второй — акций.
Тогда первый продал акций,
второй — акций.
То, что сумма от продажи
акций, полученных вторым брокером, на 140% превысила сумму, полученную
первым брокером, означает: сумма, полученная вторым брокером, больше
суммы, полученной первым, в 2,4 раза:
Так как цена одной
акции у обоих брокеров одинакова, а полученные суммы прямо пропорциональны
количеству акций, проданных каждым брокером, то
Если —
коэффициент пропорциональности количества акций, купленных брокерами,
то ими приобретено акций
на сумму 3640 р. Следовательно, на тот момент цена каждой акции составляла:
р.
Первый брокер продал акций,
второй акций.
Всего было продано акций.
К моменту продажи цена одной акции стала
(р),
т.е. на (р)
выше.
Значит, цена одной
акции возросла на 37,5%
Второй способ (преобладает алгебраический
подход).
Пусть р.
— первоначальная цена одной акции, —
количество акций, купленных первым брокером, —
количество акций, купленных вторым брокером. И пусть цена одной акции
возросла на %.
Тогда: (1)
Со временем цена
одной акции выросла до рублей.
Первый брокер продал
акций на сумму рублей,
а второй брокер — на рублей.
Согласно условию задачи
имеем: т.е.
(2)
Так как сумма от продажи
акций, полученная вторым брокером, на 140% превысила сумму, полученную
первым брокером, то
Подставив полученное
значение в
уравнение (1), будем иметь:
Подставим то же значение в
уравнение (2):
А значение нами
найдено выше.
Следовательно,
Ответ: 37,5.
№4.Задание
17 № 506090. 31 декабря 2013 года
Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%),
затем Сергей переводит в банк определённую сумму ежегодного платежа.
Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг
тремя равными ежегодными платежами?
Решение.
Пусть сумма кредита равна a,
ежегодный платеж равен x рублей, а годовые составляют k %.
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1
+ 0,01k. После первой выплаты сумма долга составит: a1 = am − x.
После второй выплаты сумма долга составит:
После третьей выплаты сумма оставшегося
долга:
По условию тремя выплатами Сергей должен
погасить кредит полностью, поэтому откуда
При a =
9 930 000 и k = 10, получаем: m = 1,1
и
Ответ: 3
993 000 рублей.
Второй способ
Пусть —
один из трёх разовых платежей. Тогда сумма долга после оплаты в первом
году составит: После
внесения второго платежа сумма долга станет равной Сумма
долга после третьего платежа: Третьим
платежом Сергей должен погасить долг, то есть долг станет равным нулю:
Третий
способ
В первый год ему начислят 993000 и сумма долга составит
10923000 минус ежегодный платеж (х) и получаем следующее 10923000-х
На второй год опять проценты и минус ежегодный платеж:
(10923000-х)*1,1-х
На третий год та же история:
((10923000-х)*1,1-х)*1,1-х=0 (так как он закрыл долг тремя равными
платежами).
Дальше нехитрые вычисления уровня средней школы и приходим
к выражению:
3,31х=13216830
Отсюда находим, что х=3993000.
№ 5.
Задание 17 № 506950. В банк помещена сумма
3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех
лет хранения после вычисления процентов вкладчик дополнительно вносил
на счет одну и ту же фиксированную сумму. К концу пятого года после начисления
процентов оказалось, что размер вклада увеличился по сравнению с первоначальным
на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?
Решение.
Общая сумма, причитающаяся
вкладчику, включая дополнительные вклады в течение четырех лет и
все процентные начисления, к концу пятого года хранения денег составляет
825 (100+725) процентов от первоначального (3900 тыс. руб.).
Эта сумма равна:
(тыс.руб.)
Некоторая часть найденной
суммы образована хранением первоначально вложенной суммы (3900
тыс.руб.) Вычислим эту часть. Поскольку процентная надбавка начислялась
в размере 50% годовых, то за 5 лет хранения этой части вклада вложенная
сумма увеличилась в раза.
То есть стала:
(тыс.
руб.)
Теперь найдем другую
часть образованной суммы с учетом дополнительных вкладов в течение
четырех лет, а также процентных начислений на эту сумму. Эта часть равна
разности двух сумм, вычисленных выше.
(тыс.
руб.)
Это — с одной стороны.
С другой же стороны эта сумма образовалась так:
Пусть вкладчик в конце
года и в течение 4 лет вносил дополнительный вклад в сумме тыс.
руб.
В конце первого года
хранения этой суммы она выросла до тыс.
руб.
Вкладчик дополнительно
внес еще тыс.
руб. На начало следующего календарного года эта часть суммы стала:
(тыс.руб.)
Через год эта сумма выросла
до:
(тыс.руб.)
Но вкладчик внес на
счет еще тыс.руб.
Сумма стала:
(тыс.
руб.)
Через год эта сумма выросла
до:
(тыс.
руб.)
Вкладчик вновь внес на
счет тыс.
руб. Часть вклада становится равной:
(тыс.руб.)
К концу последнего
года хранения всего вклада эта часть вырастает до:
(тыс.
руб.)
Теперь решим уравнение:
Итак, искомая сумма
равна 210 тыс. руб.
Ответ: 210
000.
№6.Задание 17 № 506948. За время хранения вклада в банке проценты по нему начислялись
ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. известно, что под действием
каждой новой процентной ставки вклад находился целое число месяцев, а
по истечении срока хранения первоначальная сумма увеличилась на Определите срок хранения вклада.
Решение.
Известно:
1. Проценты на вклад
начислялись ежемесячно.
2. Каждая последующая
процентная надбавка по истечении календарного месяца начислялась
с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.
Если первоначальная
сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась месяцев,
то вклад ежемесячно увеличивался в раз,
и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.
При изменении процентной
надбавки с 5% на 12% (ставка 12% продержалась месяцев)
первоначальная сумма вклада за месяцев
увеличится в раз.
Предположим, что процентная
ставка продержалась
месяцев,
а процентная ставка продержалась
месяцев.
Тогда соответствующие коэффициенты повышения составят:
и
Таким образом, коэффициент
повышения суммы вклада в целом за весь период хранения вклада в банке
составит:
Это — с одной стороны.
Но с другой стороны, согласно условию задачи первоначальная сумма
вклада за это же время увеличилась на т.е.
в
(
раз).
Значит,
Согласно основной
теореме арифметики каждое натуральное число, большее 1, можно представить
в виде произведения простых множителей, и это представление единственное
с точностью до порядка их следования. В таком случае:
Решим эту систему относительно
натуральных и
Из последнего уравнения
системы имеем: При
этих значениях и
система
примет вид:

Итак, вклад
в банке на хранении был 7 месяцев. При найденных значениях и
действительно
равно нулю.
Ответ: 7.
№7.Задание
17 № 506954. В конце августа 2001
года администрация Приморского края располагала некой суммой денег,
которую предполагалось направить на пополнение нефтяных запасов
края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив
закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно,
что сумма вклада в банке увеличивалась первого числа каждого месяца
на 26% по отношению к сумме на первое число предыдущего месяца, а цена
барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов
больше (от первоначального объема закупок) руководство края смогло
пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную
из банка вместе с процентами, и направив ее на закупку нефти?
Решение.
Пусть сумма, которой
первоначально располагала администрация края, составляла у.е.,
а цена барреля сырой нефти у.е.
Тогда первоначально возможный объем закупок составлял баррелей.
Этот объем примем за 100 процентов. За 2 месяца хранения в банке положенная
сумм выросла до у.е.,
а цена барреля сырой нефти за это же время убыла до у.е.
Следовательно, 1 ноября 2001 г. руководство края на эту сумму могла закупить баррелей
сырой нефти. Процентное отношение этого объема к первоначально возможному
объему закупок составит:
%
то есть %
= %.
Значит, руководство
края смогло пополнить 1 ноября 2001 г. нефтяные запасы края на 96%
больше, чем 1 сентября того же года.
Ответ: 96.
№8.Задание
17 № 506957. Сергей взял кредит в
банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося
долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную
Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются
так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно,
то есть на одну и ту же величину.
Сколько процентов от
суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх
кредита)?
Решение.
Предложение «Суммы,
выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате
сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же
величину» означает: Сергей взятую сумму возвращал равными долями.
Общая сумма, уплаченная
Сергеем банку сверх кредита, обусловлена только применением процентной
ставки.
В первом месяце эта
часть заплаченной суммы составляла , во
втором — в
третьем — в
восьмом — наконец,
в последнем —
Всего за 9 месяцев:
Искомое процентное
отношение есть 60
Ответ: 60.
№9.Задание
17 № 507913. Оля хочет взять в кредит
1 200 000 рублей. Погашение кредита происходит раз в год равными суммами
(кроме, может быть, последней) после начисления процентов. Ставка процента
10 % годовых. На какое минимальное количество лет может Оля взять кредит,
чтобы ежегодные выплаты были не более 320 000 рублей?
Решение.
Пусть сумма кредита
равна S, а годовые составляют a %. Тогда в последний
день каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a Составим
таблицу выплат.
|
Год |
Долг банку (руб.) |
Остаток доли после выплаты (руб.) |
|
0 |
1200000 |
– |
|
1 |
1320000 |
1000000 |
|
2 |
1100000 |
780000 |
|
3 |
858000 |
538000 |
|
4 |
591800 |
271800 |
|
5 |
298980 |
0 |
Значит, Оля погасит
кредит за 5 лет.
Ответ: 5.
Задание 17 № 506955. Транcнациональная
компания Amako inc. решила провести недружественное поглощение компании
First Aluminum Company (FAC) путем скупки акций миноритарных акционеров.
Известно, что Amako inc. было сделано три предложения владельцам акций
FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3, а
общее количество приобретенных Amako inc. акций поглощаемой компании
увеличивалась на 20%. Определите величину третьего предложения и
общее количество скупленных акций First Aluminum Company, если начальное
предложение составляло $27 за одну акцию, а количество акций, выкупленных
по второй цене, 15 тысяч.
Решение.
|
Предложения |
Цена одной акции ($) |
Количество выкупленных акций |
|
|
При данном предложении |
Общее количество |
||
|
1 |
27 |
75000 |
75000 |
|
2 |
36 |
15000 |
90000 |
|
3 |
48 |
Для получения ответа вычисление не требуется |
108000 |
Ответ:
третье предложение по цене $48 за одну акцию; общее количество выкупленных
акций 108000.
№ 10.Задание
17 № 506951. Банк под определенный
процент принял некоторую сумму. Через год четверть накопленной суммы
была снята со счета. Банк увеличил процент годовых на 40%. К концу следующего
года накопленная сумма в 1,44 раза превысила первоначальный вклад.
Каков процент новых годовых?
Решение.
Пусть банк первоначально
вклад в размере у.е.
принял под годовых.
Тогда к началу второго года сумма стала у.е.
После снятия четверти
накопленной суммы на счету осталось у.е.
С момента увеличения
банком процентной ставки на 40% к концу второго года хранения остатка
вклада накопленная сумма стала
у.е.
По условию задачи
эта сумма равна у.е.
Решим уравнение
;
Этот корень не подходит
по смыслу задачи: Новые
годовые составляют 20 + 40 = 60 %.
Ответ: 60.
№ 11.Задание
17 № 506958. Антон взял кредит в
банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося
долга увеличивается на одно и то же число процентов (месячную процентную
ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые
в конце каждого месяца, подбираются так, чтобы в результате сумма
долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную
процентную ставку.
Решение.
Пусть сумма кредита у.е.,
процентная ставка банка %.
Предложение «Суммы,
выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате
сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же
величину» означает: Антон взятую сумму возвращал в банк равными долями.
Сумма, образованная применением процентной ставки, составляет:
(у.е.)
Общая сумма, выплаченная
Антоном за 6 месяцев: (у.е.).
А эта сумма по условию задачи равна у.е.
Решим уравнение:
Ответ: 18.
№12.Задание
17 № 506953. В январе 2000 года
ставка по депозитам в банке «Возрождение» составила х %
годовых, тогда как в январе 2001 года — у % годовых, причем
известно, что x + y = 30%. В январе 2000
года вкладчик открыл счет в банке «Возрождение», положив на него некоторую
сумму. В январе 2001 года, по прошествии года с того момента, вкладчик
снял со счета пятую часть этой суммы. Укажите значение х при
котором сумма на счету вкладчика в январе 2002 года станет максимально
возможной.
Решение.
Через лет
на первом счёте будет сумма
В это же время на втором
счёте будет сумма
Приравняем эти суммы
и решим полученное уравнение:
Таким образом, суммы
на счетах сравняются через 12 лет после открытия первого вклада.
Ответ: 12.
Рациональное натуральное
число 506957
– составное.
Произведение и сумма цифр: 0, 32.
У числа 506957 8 делителей: 1, 11, 17, 187, 2711, 29821, 46087, 506957.
585792 — сумма делителей числа.
506957 и 0.00000197255388524076 являются взаимно обратными числами.
Число в других системах счисления:
двоичный вид числа: 1111011110001001101, троичный вид числа: 221202102012, восьмеричный вид числа: 1736115, шестнадцатеричный вид числа: 7BC4D.
Число байт 506957 – это 495 килобайтов 77 байтов .
Азбука Морзе для числа: ….. —— -…. —-. ….. —…
Число не является числом Фибоначчи.
Косинус 506957: -0.2335, тангенс 506957: 4.1636, синус 506957: -0.9723.
У числа есть натуральный логарифм: 13.1362.
Десятичный логарифм числа: 5.7050.
712.0091 — квадратный корень, 79.7365 — кубический.
Число 506957 в секундах это 5 дней 20 часов 49 минут 17 секунд .
В нумерологии число 506957 означает цифру 5.
Решение и ответы заданий Варианта №3 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.

Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
Площадь ромба равна 10. Одна из его диагоналей равна 8. Найдите другую диагональ.
Задание 2.
Длина окружности основания цилиндра равна 5, высота равна 6. Найдите площадь боковой поверхности цилиндра.
Задание 3.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,83. Вероятность того, что окажется меньше 10 пассажиров, равна 0,46. Найдите вероятность того, что число пассажиров будет от 10 до 20.
Задание 4.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Биолог» выиграет жребий ровно два раза.
Задание 5.
Найдите корень уравнения cosfrac{pi(2x–6)}{6}=frac{sqrt{3}}{2}. В ответе запишите наибольший отрицательный корень.
Задание 6.
Найдите значение выражения frac{4^{4,75}}{8^{2,5}}.
Задание 7.
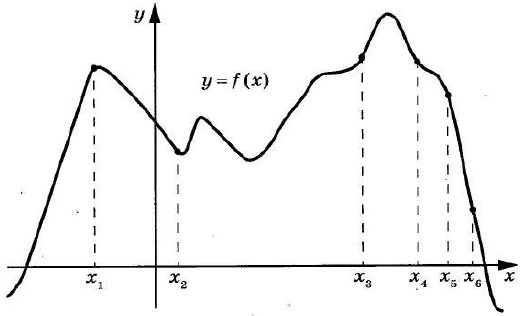
На рисунке изображён график функции y = f(x). На оси абсцисс отмечено шесть точек: x1, x2, x3, x4, x5, x6. В ответе укажите количество точек (из отмеченных) в которых производная функции f(x) положительна?
Задание 8.
Наблюдатель находится на высоте h, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле l=sqrt{frac{Rh}{500}}, где R = 6400 км – радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 25,6 километра? Ответ дайте в метрах.
Задание 9.
Заказ на изготовление 238 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 3 детали больше?
Задание 10.
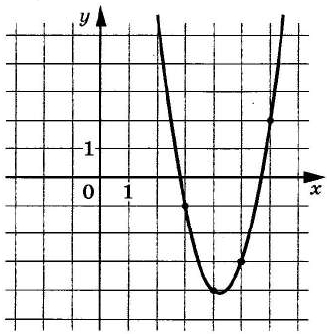
На рисунке изображён график функции f(x) = ax2 + bc + c. Найдите с.
Задание 11.
Найдите наибольшее значение функции y = ln(x + 18)12 − 12x на отрезке [−17,5;0].
Задание 12.
а) Решите уравнение 4^{x+sqrt{x}–1,5}+3cdot 4^{x–sqrt{x}+1,5}-4^{x+1}=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [2; 6].
Задание 13.
В прямой пятиугольной призме ABCDEA1B1C1D1E1, высота АА1, равна 3√5, BC = CD = 6, а четырехугольник ABDE прямоугольник со сторонами АВ = 5 и AE = 4√5.
а) Докажите, что плоскости СA1E1 и AED1 перпендикулярны.
б) Найдите объём многогранника CAED1B1.
Задание 14.
Решите неравенство logtg3,2 (log3 (9 – x2)) ≥ 0.
Задание 15.
В июле Максим планирует взять кредит в банке на некоторую сумму. Банк предложил Максиму два варианта кредитования.
1-й вариант:
– кредит предоставляется на 3 года;
– в январе каждого года действия кредита долг увеличивается на 20% от суммы долга на конец предыдущего года;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платеж должен погасить долг по кредиту полностью,
2-й вариант:
– кредит предоставляется на 2 года:
– в январе каждого года действия кредита долг увеличивается на 24 %;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Максим подсчитал, то выяснил, что по 1-му варианту кредитования ему придется выплачивать на 373 600 рублей больше, чем по 2-му варианту. Какую сумму Максим планирует взять в кредит?
Задание 16.
Четырёхугольник ABCD со сторонами ВС = 7 и AB = CD = 20 вписан в окружность радиусом R = 16.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
frac{log_{0,4}(6x^{2}–13x+5ax–6a^{2}–13a+6)}{sqrt{2x–3a+4}}=0
имеет единственный корень.
Задание 18.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 9177.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки. Ответами к заданиям 1–22 являются последовательность цифр, число или слово (словосочетание). Ответы запишите в поля ответов в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ № 1 справа от номеров соответствующих заданий, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Скачать тренировочный вариант ЕГЭ: Скачать
Скачать ответы на тренировочный вариант ЕГЭ: Скачать
Задания:
1. Рассмотрите таблицу «Методы биологических исследований» и заполните ячейку, вписав соответствующий термин. Применяется для выявления геномных мутаций.
2. Исследователь добавлял в стакан коровьего молока желудочный сок собаки. Как спустя час в стакане изменится содержание дисахарида лактозы и животных жиров? Для каждой величины определите соответствующий характер её изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
3. Площадь земель, покрытых лесом, в России составляет примерно 1200 млн га. Известно, что 12 га леса связывают 18 тонн диоксида углерода в год. Сколько млн тонн углекислого газа может быть связано за год за счет российских лесов?
4. Определите вероятность (в %) гибели от анемии ребенка, родившегося в браке гомозиготных по рецессивному аллелю родителей, если эта форма анемии наследуется как аутосомный доминантный признак. В ответ запишите только соответствующее число.
5. Каким номером на рисунке обозначена структура, образующая спираль в сперматозоидах млекопитающих?
6. Установите соответствие между характеристиками и структурами, обозначенными на рисунке цифрами 1, 2, 3, 4: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
7. Выберите три признака, которые соответствуют описаниям селекции. Запишите в таблицу цифры, под которыми они указаны.
1) выведение новых штаммов микроорганизмов
2) получение новых семейств растений
3) получение генномодифицированных растений
4) выведение тритикале при скрещивании пшеницы и ржи
5) получение рекомбинантной плазмиды
6) выведение пород животных и сортов растений
8. Установите последовательность этапов ферментативного катализа. Запишите в таблицу соответствующую последовательность цифр.
1) образование нестабильного комплекса фермент-продукт
2) сближение фермента и субстрата
3) начало распада комплекса фермент-продукт
4) формирование фермент-субстратного комплекса
5) высвобождение продукта и фермента
9. Какой цифрой на рисунке обозначена вторичная полость тела?
10. Установите соответствие между характеристиками и структурами тела дождевого червя, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
11. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Для растения, изображенного на рисунке, характерно:
1) гаметофит обоеполый — содержит архегонии и антеридии
2) дихотомическое ветвление
3) заросток сердцевидной формы
4) споры созревают в сорусах
5) споры образуются в спороносных колосках
6) гаметофит формирует вайи
12. Установите последовательность систематических групп, начиная с самого низкого ранга. Запишите в таблицу соответствующую последовательность цифр.
1) Эукариоты
2) Членистоногие
3) Ежемухи
4) Ежемуха свирепая
5) Двукрылые
6) Животные
13. Какой цифрой на рисунке указан тип научения, который изучал К. Лоренц?
14. Установите соответствие между характеристиками и типами научения, обозначенными на рисунке выше цифрами 1, 2, 3: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
15. Выберите три верно обозначенные подписи к рисунку «Строение уха». Запишите цифры, под которыми они указаны.
1) серная (церуминозная) железа
2) наружный слуховой проход
3) слуховая косточка
4) овальное окно
5) преддверно-улитковый нерв
6) улитка
16. Установите последовательность событий, происходящих при свертывании крови. Запишите в таблицу соответствующую последовательность цифр.
1) разрушение тромбоцитов у места повреждения
2) превращение протромбина в тромбин
3) уплотнение рыхлой пробки тромбоцитов фибриновыми нитями
4) превращение фибриногена в фибрин
5) выделение тромбопластина
6) образование тромба
17. Прочитайте текст. Выберите три предложения, в которых даны описания географического видообразования. Запишите цифры, под которыми они указаны. (1)Видообразование происходит в результате расширения ареала исходного вида или при попадании популяции в новые условия. (2)Такое видообразование называют аллопатрическим. (3)Примером видообразования служит формирование двух подвидов погремка большого на одном лугу. (4)Естественный отбор способствовал формированию двух рас севанской форели, нерестящихся в разное время. (5)Репродуктивная изоляция особей не является обязательным условием видообразования. (6)Результатом изоляции является формирование эндемичных островных видов животных.
18. Выберите три верных ответа из шести и запишите в таблицу цифры, под которыми они указаны. Примеры антропогенных факторов воздействия:
1) разрушение озонового слоя под действием фреонов
2) гибель сусликов из-за пандемии
3) нарушение режима рек под влиянием деятельности бобров
4) разрыхление почв дождевыми червями
5) эвтрофикация водоемов из-за смыва удобрений
6) металлизация атмосферы
19. Установите соответствие между типами взаимоотношений и организмами, между которыми они устанавливаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
20. Установите последовательность этапов эволюции животных, начиная с самых древних представителей. Запишите соответствующую последовательность цифр.
1) стегоцефал
2) зверозубый ящер
3) тушканчик
4) сеймурия
5) кистеперая рыба
21. Проанализируйте таблицу «Роль прокариотов в экосистемах». Заполните пустые ячейки таблицы, используя элементы, приведённые в списке. Для каждой ячейки, обозначенной буквой, выберите соответствующий элемент из предложенного списка. Список элементов:
1) Редуценты
2) Бактерии-хемосинтетики
3) Продуценты
4) Гетеротрофы
5) Бактерии-фотосинтетики
6) Денитрифицирующие
7) Автотрофы

22. Проанализируйте диаграмму, отражающую содержание холестерола ЛПНП (липопротеинов низкой плотности) в плазме крови обследованных в лаборатории людей. Выберите все утверждения, которые можно сформулировать на основании анализа представленных данных. Запишите в ответе цифры, под которыми указаны выбранные утверждения.
1) Пятеро из обследованных людей имеют значение содержания холестерола-ЛПНП в интервале от 200 до 249 мг/дл.
2) Более 60% пациентов имеют чрезвычайно высокий риск развития атеросклероза.
3) Значение содержания холестерола-ЛПНП более 300 мг/дл смертельно.
4) Более 50% обследованных людей имеют от 75 до 149 мг/дл холестеролЛПНП в плазме крови.
5) В плазме крови 4% людей содержание холестерола-ЛПНП находится в пределах от 50 до 74 мг/дл.
23. Какая переменная в этом эксперименте будет зависимой (изменяющейся), а какая — независимой (задаваемой)? Объясните, как в данном эксперименте можно поставить отрицательный контроль. С какой целью необходимо такой контроль ставить? * Отрицательный контроль – это экспериментальный контроль, при котором изучаемый объект не подвергается экспериментальному воздействию при сохранении всех остальных условий.
24. Предположите, почему для обработки кукурузных полей используют 2,4- Д. Каким веществом по результату действия на двудольные растения является 2,4-дихлорфеноксиуксусная кислота?
25. Рассмотрите рисунок. Какие пары комплементарных азотистых оснований ДНК отмечены буквами А и Б? При содержании большего количества каких пар азотистых оснований молекула ДНК будет медленнее подвергаться денатурации при воздействии повышенной температуры? Ответ поясните.
26. Некоторые виды лишайников являются трехкомпонентными, то есть включают клетки трех видов организмов: гриба, зеленой водоросли и цианобактерии. Какие функции могут выполнять цианобактерии в составе такого лишайника? Назовите не менее двух. Какие преимущества имеет гриб в составе трехкомпонентного лишайника по сравнению с двухкомпонентным?
27. У животных существует несколько типов брачных отношений, например, моногамия – образование стойких супружеских пар, полигамия – спаривание особи одного пола со множеством партнеров противоположного пола. Большинство видов гнездовых птиц практикуют моногамные отношения, а большинство видов млекопитающих — полигамные. Объясните, почему для гнездовых птиц стратегия моногамного поведения наиболее выгодна. По каким причинам птицы, как правило, не могут практиковать полигамию, как это делают млекопитающие? Ответ поясните.
28. Какой хромосомный набор (n) характерен для клеток мегаспорангия и мегаспоры цветкового растения? Объясните, из каких исходных клеток и в результате какого деления образуются клетки мегаспорангия и мегаспора.
29. Существует два вида наследственной слепоты, каждый из которых определяется рецессивными аллелями генов (а или b). Оба аллеля находятся в различных парах гомологичных хромосом. Какова вероятность рождения слепой внучки в семье, в которой бабушки по материнской и отцовской линиям хорошо видят (не имеют рецессивных генов), а оба дедушки дигомозиготны и страдают различными видами слепоты? Составьте схему решения задачи. Определите генотипы и фенотипы бабушек и дедушек, их детей и возможных внуков.
Вам будет интересно:
ЕГЭ по биологии 11 класс 2023. Новый тренировочный вариант №6 — №221121 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
Варианты заданий и ответы для вариантов РЯ (РУ) 2210501 и РЯ (РУ) 2210502 диагностическая работа №2 статград пробный ЕГЭ 2023 по русскому языку 11 класс в формате реального экзамена ЕГЭ 2023 года, которая прошла 16 февраля 2023 года.
Скачать тренировочные варианты
Скачать ответы для вариантов
2210501_2210502_русский_язык_егэ2023
Вариант РЯ2210501 с ответами
В книгу избранных сочинений А.М. Ремизова вошли произведения различных жанров и стилей. Стараясь расширить представления о творческой палитре писателя, мы включили в сборник ряд не переиздававшихся в наше время вещей. К ним относятся апокриф «Вéщица» (образец одной из «отречённых повестей», составляющих книгу «Лимонарь»), рассказы «Пожар» и «Занофа», отражающие характерную для раннего Ремизова символико-экспрессивную манеру, рассказ «Жертва», представляющий жанр неоготического, «страшного» рассказа. Сборник «Мартын Задека», также включённый в книгу, позволяет оценить стиль позднего Ремизова и знакомит читателя с уникальным литературным жанром – жанром снов.
<…> (кроме рассказа «Петушок») дореволюционные произведения публикуются по изданию: Ремизов А. Сочинения: [в 8 т.]. СПб: Шиповник, 1910–1912 (далее: Сочинения – с указанием соответствующего тома). Отказ от публикации этих текстов в поздних редакциях (то есть от соблюдения принципа последней авторской воли) связан со стремлением составителей достичь определённой стилевой цельности. Дело в том, что при переиздании своих произведений Ремизов каждый раз стремится включить их в единое целое новой книги или нового цикла, поэтому даже незначительная стилевая правка оказывается важной для текстов этого автора. (По М. Козьменко и И. Кашириной)
1. Самостоятельно подберите определительное местоимение, которое должно стоять на месте пропуска в первом (1) предложении последнего абзаца текста. Запишите это местоимение.
2. В тексте выделено пять слов. Укажите варианты ответов, в которых лексическое значение выделенного слова соответствует его значению в данном тексте. Запишите номера ответов.
- 1) СОЧИНЕНИЕ. Вид письменной школьной работы – изложение своих мыслей, знаний на заданную тему. Классное с.
- 2) ПРЕДСТАВЛЕНИЕ. Знание, понимание чего-нибудь. Не иметь никакого представления о чём-н. Составить себе п. о чём-нибудь. Книга даёт хорошее п. о предмете.
- 3) ВЕЩЬ. Нечто, обстоятельство, явление. Произошла непонятная в. Прекрасная в. – молодость!
- 4) ПОЗДНИЙ. Приходящий после обычного или нужного времени, запоздалый. П. гость. Позднее раскаяние.
- 5) ВОЛЯ. Желание, требование, хотение; сознательное стремление к осуществлению чего-либо. Исполнять волю народа.
3. Укажите варианты ответов, в которых даны верные характеристики фрагмента текста. Запишите номера ответов.
- 1) Язык приведённого фрагмента отличается эмоциональностью и экспрессивностью, использованием олицетворения (знакомит читателя с уникальным литературным жанром) и эпитетов («неоготического… рассказа», «стилевой цельности»), что указывает на субъективность излагаемой информации.
- 2) Использование отглагольных существительных (представления, соблюдение и др.), терминов (символико-экспрессивную манеру, рассказ, жанр, цикл), а также обособленных распространённых согласованных определений и вставных конструкций свидетельствует о принадлежности текста к научному стилю.
- 3) Ведущий тип речи в тексте – рассуждение, что характерно для репортажа – жанра, к которому относится данный фрагмент.
- 4) В представленном фрагменте авторы придерживаются норм официальноделового стиля, обращая внимание в первую очередь на фактическую сторону дела, чему способствует отсутствие местоимений 1-го и 2-го лица, употребление вместо них специальных обозначений (писатель, составители).
- 5) Текст адресован узкому кругу специалистов и написан терминологически точным языком.
4. Укажите варианты ответов, в которых верно выделена буква, обозначающая ударный гласный звук. Запишите номера ответов.
- 1) поднЯв
- 2) прИнятый
- 3) свеклА
- 4) стОляр
- 5) ворвалАсь
5. В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите подобранное слово. Тогда ещё доживали на ферме оставшиеся с прежних времён лошадитяжеловозы – красивые и благородные свидетели прежнего ЖИЗНЕННОГО уклада. От природы он был наделён дружеской сердечностью, крепкой памятью и ДЕЛОВОЙ хваткой. У меня есть ЖЕСТОКОЕ правило: никогда не делать того, что могут сделать мои подчинённые. ЛЕДОВАЯ разведка была проведена лётчиком М.С. Бабушкиным на самолёте, находившемся на борту «Челюскина». Я ожидал увидеть необычного человека, но в комнате появилось совершенно БЕЗЛИКОЕ существо, с водянистыми глазами и прозрачным лицом, на котором застыла презрительная маска равнодушия.
6. Отредактируйте предложение: исправьте лексическую ошибку, заменив неверно употреблённое слово. Запишите подобранное слово, соблюдая нормы современного русского литературного языка. Федя был не хрупкого десятка, но в его взгляде было то, от чего дрогнуло бы сердце самого равнодушного человека.
7. В одном из выделенных ниже слов допущена ошибка в образовании формы слова. Исправьте ошибку и запишите слово правильно.
- более СЛАБ физически
- к ДВЕ тысячи восьмому году
- КОЛЫШЕТСЯ на ветру
- сливочные КРЕМЫ
- отряд ПАРТИЗАНОВ
9. Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) ч..порный (вид), ш..лковый (ковёр), ч..рствый (хлеб)
- 2) оп..рившиеся (птенцы), вин..грет, накр..нённый (влево)
- 3) сброш..рованный (экземпляр), (новогодняя) миш..ра, биж..терия
- 4) облок..титься, ут..пический, (народное) оп..лчение
- 5) разм..нать, инж..нер, выт..реть (руки)
10. Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) без..мянные (герои), дез..нформация, вз..сканный (налог)
- 2) пр..словутый, пр..стижный, пр..подавать
- 3) из..ять, двух..ярусный, пред..явитель
- 4) и..жаленный (крапивой), обе..доленный, не..держанность
- 5) о..душина, по..текст, по..делывать (документ)
11. Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) навязч..вый, екатеринбурж..нка
- 2) нищ..нский, (чайное) сит..чко
- 3) коч..вой, потч..вать
- 4) вермишел..вый, масл..нистый
- 5) бельч..нок, пастуш..нок
12. Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) ве..щий (прохладой), (волны) трепл..т (лодку)
- 2) высто..шь (в борьбе), разгоня..шься
- 3) услыш..нный, корч..щийся (от боли)
- 4) заверт..шься, обанкрот..вшийся
- 5) распояс..вшись, (они) покрош..т (хлеб)
13. Определите предложение, в котором НЕ с выделенным словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. Иван был удивлён: помещение (НЕ)ЗАПЕРТО, внутри горит свет, а хозяев нет. И был зимой обильный снег, а на нём – заячьи следы, но на зайца (НЕ)ВСЯКИЙ мужик охотится. Отец за всё брался с жаром, а Вялов работал (НЕ)ХОТЯ, как бы из милости. Он полжизни отработал в цеху на подхвате, так и (НЕ)СТАВ мастером. Декоративный эффект верескового сада, зарослей рододендронов или соснового бора (НЕ)ХУЖЕ привычного садового ландшафта.
14. Определите предложение, в котором оба выделенных слова пишутся СЛИТНО. Раскройте скобки и выпишите эти два слова. С нашей стороны (НА)ВСТРЕЧУ с румынским парламентёром был (С)НОВА отправлен Иннокентьев. Кто-то из туристов забыл на привале сумку с консервами, и (ПО)ЭТОМУ провизии оставалось (В)ОБРЕЗ. Он сидел (С)БОКУ стола и (БЕЗ)УСТАЛИ названивал в бухгалтерию. Мастеровой удивлённо поднял глаза (В)ВЕРХ и (ТОТ)ЧАС поразился, обрадовался. (В)ТЕЧЕНИЕ всего семейного вечера сестра рассказывала, как (ВО)ВРЕМЯ войны дед привёл в дом беспризорника.
15. Укажите все цифры, на месте которых пишется одна буква Н. Головной убор, повяза(1)ый на лоб, – изыска(2)ое сочетание широкого, украше(3)ого зубцами венца с золочё(4)ой полотня(5)ой лентой – придавал своей обладательнице величестве(6)ость, превращая её в утончё(7)ую сказочную фею.
16. Расставьте недостающие знаки препинания. Укажите предложения, в которых нужно поставить ОДНУ запятую. Запишите номера этих предложений.
- 1) В комнате тихо играла джазовая музыка и жужжала назойливая муха.
- 2) На празднике в честь Дня защиты детей выступил замечательный семейный фольклорный ансамбль «Живица».
- 3) Инициатива была на стороне наших спортсменов и важно было её умело использовать и не обмануть ожидания болельщиков.
- 4) Духовный образ этого кроткого человека давно уже обрисован полно и верно и мои заметки о недолгом общении с ним могут лишь добавить мелкие штрихи к портрету.
- 5) Егоров производил впечатление обременённого жизненным опытом интеллигента и его влияние на учеников и коллег было благотворным.
17. Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложениях должна(-ы)стоять запятая(-ые). Дойдя до центрального парка (1) и остановившись перед украшенной мерцающими огнями аркой (2) Данила (3) одетый в лёгкий полушубок (4) и замёрзший до полусмерти (5) искал и не находил брата среди праздничной толпы (6) плотным потоком (7) двигавшейся через распахнутые ворота главного входа к сцене.
18. Расставьте все недостающие знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложениях должна(-ы) стоять запятая(-ые). Теоретически, вылетев со скоростью света в одном направлении, в конце концов прибудешь, как Магеллан, в отправную точку. Жаль, что не только сам ты за время это кончишься, но и вся вселенная. Так что подобный план (1) даже (2) в случае расцвета звездоплавания не пригодится. Браво (3) мудрый мой (4) астрофизик. Но посоветуй (5) всё-таки, как обнаружить его, четвёртое? Пролетает чёрная птица, вероятно скворец, над весенней улицей. Ночь в руках – гуттаперчевый шар, слюдяные блёстки, а днём стелется дым от сожжённой листвы по окрестным дачам. Пахнет корицею, мокрым снегом, терпким вином. Словом (6) всем, чего не храним, а потерявши – плачем. (По Б. Кенжееву)
19. Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Истинными обитателями дома были желтоватые и бурые настенные фотографии (1) каких-то людей (2) зыбкая семейная память (3) о которых (4) слабела с каждым поколением (5) и в скором времени могла исчезнуть бесследно.
20. Расставьте знаки препинания: укажите все цифры, на месте которых в предложении должны стоять запятые. Тут Клэр разразилась бурными рыданиями и попрёками (1) из которых следовало (2) что ей не доводилось ещё так бездарно проводить время (3) с тех пор как её заставляли часами играть гаммы (4) и повторять один и тот же пассаж (5) и (6) если вспоминать всё (7) на что она до сих пор обижена (8) то не хватит целой жизни.
21. Найдите предложения, в которых запятая(-ые) ставится(-ятся) в соответствии с одним и тем же правилом пунктуации. Запишите номера этих предложений. (1)Осенний период свадеб и гуляний молодёжи завершали Кузьминки – день бессребреников Косьмы и Дамиана, называемый «Курячьими именинами». (2)Образ Косьмы и Дамиана, святых врачей и чудотворцев, в русской традиции превратился в культ ремесленников Кузьмы и Демьяна, божьих кузнецов, которые работали не за вознаграждение и в народном сознании сливались в одно лицо. (3)День Кузьмы и Демьяна стал праздником кузнецов (по созвучию Кузьма – кузнец) и считался началом предзимья, когда, по народному поверью, божьи кузнецы сковывали «зимними цепями» земли и реки. (4)Кузьма и Демьян не только ковали зимние латы для рек и водоёмов, но и были «свадебными кузнецами» – выковывали свадебные венцы и брачные узы. (5)В этот день в Москве, в Толмачёвском переулке, женщины собирались вокруг церкви Космы и Дамиана с курами и после обедни служили молебны. (6)В сёлах крестьяне приходили на боярский двор и с челобитьем подносили кур своей боярыне «на красное житьё». (7)Девушки в продолжение трёх вечеров устраивали кузьминскую вечеринку – посиделки, обязательными обрядовыми блюдами на которых были куриная лапша и пиво. (8)Часто они продавали угощение парням за несколько копеек, а хозяйка вечерницы делила вырученные деньги между присутствующими.
22. Какие из высказываний не соответствуют содержанию текста? Укажите номера ответов.
- 1) Молодой человек искренне хотел помочь Анне Вячеславовне.
- 2) Поэт Симонов по просьбе Алёши оставил автограф в книге
- 3) Анна Вячеславовна долгие годы хранила драгоценную для неё книгу с автографом Симонова.
- 4) Став жертвой обмана, героиня особенно остро осознала, как дороги ей вещи, нажитые вместе с мужем.
- 5) Сын Анны Вячеславовны не хотел помогать ей деньгами.
23. Какие из перечисленных утверждений являются верными? Укажите номера ответов.
- 1) Предложение 3 содержит следствие того, о чём говорится в предложении 2.
- 2) Предложения 11–13 содержат повествование.
- 3) Предложение 28 содержит описание.
- 4) В предложениях 42–46 представлено описание.
- 5) В предложениях 77, 78 представлено рассуждение.
24. Из предложений 74–76 выпишите одно разговорное слово.
25. Среди предложений 39–45 найдите такое(-ие), которое(-ые) связано(-ы) с предыдущим при помощи форм(-ы) слов(-а). Напишите номер(-а) этого(-их) предложения(-ий).
26. «Пронзительная история одинокой пожилой женщины передана живым и в то же время простым языком. Автор использует такие тропы, как (А) (“словоохотливая владелица” в предложении 9, “статный Алёша” в предложении 28) и (Б) (“дала… телефон” в предложении 10, “голос… внушал доверие” в предложении 12, “любит Симонова” в предложении 49), чтобы создать яркие образы персонажей. В этом ему помогает и приём – (В) (предложения 76, 77). Речь героев насыщена таким лексическим средством, как (Г) (“не может быть и речи” в предложении 9, “на чёрный день” в предложении 20), что делает персонажей более близкими, понятными читателю».
27. Напишите сочинение по прочитанному тексту. Сформулируйте одну из проблем, поставленных автором текста. Прокомментируйте сформулированную проблему. Включите в комментарий два примера-иллюстрации из прочитанного текста, которые важны для понимания проблемы исходного текста (избегайте чрезмерного цитирования). Дайте пояснение к каждому примеру-иллюстрации. Проанализируйте смысловую связь между примерами-иллюстрациями.
Вариант РЯ2210502 с ответами
Корреспондент. Вы – русский поэт, пишущий сложные, философские стихи. Труднодоступные неподготовленному читателю. Я сейчас становлюсь на точку зрения массового читателя, которому и вообще не до стихов, а в эмиграции – и подавно. И.А. Бродский. Да, здесь больше пишущих, чем читающих. Корреспондент. Так вот, в этой обстановке читательской инертности, с одной стороны, и ожесточённой борьбы за русскоязычного читателя – с другой, вы одерживаете одну блестящую победу за другой. Как вы сами это объясняете? Каков механизм вашего успеха? И.А. Бродский. Никакого особенного механизма нет.
Просто, если это действительно, так сказать, успех, то всё объясняется простым фактом, а <…> тем, что мои сочинения, статьи, стихи печатаются в англоязычной прессе довольно широко. И, видимо, не кажутся непонятными. Многое значит хороший перевод. Мой учитель, поэт Давид Самойлов, говорил, что хороший перевод сохраняет семьдесят процентов подлинника. У меня хорошие переводчики, и я сам часто помогаю им. Конечно, в любом, даже самом совершенном переводе, вещь теряет. Корреспондент. Есть вообще поэты, не поддающиеся переводу. Пушкин например. И.А. Бродский. Последний из переводов «Евгения Онегина», перевод Джонстона, – отличный. Корреспондент. В рифму? И.А. Бродский. Да ещё в какую! Его можно в местной средней школе преподавать. Корреспондент.
Критики считают, что вы взорвали традиционный, классический русский стих, лишив его основного атрибута – строки как «единицы поэзии», и тем приблизили к прозе. Считаете ли вы это мнение правильным? И.А. Бродский. Ничего я русский стих не лишал и ничего в нём не взрывал. У каждого человека своя дикция, и у меня, видимо, тоже своя. Про приближение к прозе я ничего сказать не могу; единственно, к чему я более или менее всегда стремился, это к логичности – хотя бы чисто внешней – поэтической речи, к договариванию вещей до конца.
1. Самостоятельно подберите уточняющую частицу, которая должна стоять на месте пропуска в четвёртом (4) абзаце текста. Запишите эту частицу.
2. В тексте выделено пять слов. Укажите варианты ответов, в которых лексическое значение выделенного слова соответствует его значению в данном тексте. Запишите номера ответов.
- 1) СЛОЖНЫЙ. Представляющий затруднения для понимания, решения, осуществления и т.п.; трудный. С. текст. Сложная проблема.
- 2) МАССОВЫЙ. Производимый в большом количестве, распространяющийся на множество, многих. Массовое производство.
- 3) ОБСТАНОВКА. Положение, обстоятельства, условия существования кого-чего-нибудь. Международная о. В обстановке гласности.
- 4) ПОМОГАТЬ. (1 и 2 л. не употр.), кому-чему. Дать желаемый результат, следствие, принести пользу. Лечение помогло.
- 5) ПОСЛЕДНИЙ. Окончательный, бесповоротный. Это моё последнее слово. Последнее решение.
3. Укажите варианты ответов, в которых даны верные характеристики фрагмента текста. Запишите номера ответов.
- 1) В репликах И.А. Бродского встречаются вводные слова и конструкции (так сказать, видимо, конечно), лексический повтор («Ничего я русский стих не лишал и ничего в нём не взрывал. У каждого человека своя дикция, и у меня, видимо, тоже своя»).
- 2) Текст интервью содержит стилевые особенности, характерные для разговорной речи: он отличается неофициальностью общения, спонтанностью, диалогичностью, ориентирован на неподготовленного читателя.
- 3) Текст относится к официально-деловому стилю, так как содержит термины (эмиграции, прессе, подлинника), собеседники используют нейтральную и специальную книжную лексику.
- 4) Речь собеседников различается: корреспондент использует эпитеты («ожесточённая борьба», «блестящая победа») и метафору (взорвать стих), Бродский же подчёркнуто ироничен (Да, здесь больше пишущих, чем читающих; Да ещё в какую! Его можно в местной средней школе преподавать).
- 5) В тексте интервью демонстрируется отстранённость собеседников, объективность излагаемой информации, что обеспечивается отсутствием слов в переносном значении, использованием фактов и числовых данных (семьдесят процентов).
4. Укажите варианты ответов, в которых верно выделена буква, обозначающая ударный гласный звук. Запишите номера ответов.
- 1) кУхонный
- 2) тУфля
- 3) кралАсь
- 4) загнУтый
- 5) дОнизу
5. В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите подобранное слово. Он бросил на друга ОПАСЛИВЫЙ взгляд и тут же отвёл глаза в сторону. Не суровый приговор, а доброе слово, дружеское участие – самые ДЕЙСТВУЮЩИЕ средства исправления. На нём его парадный суконный костюм, ЛАКОВЫЙ козырёк фуражки бросает на лоб короткую тень. Если площадь помещения не превышает 20 квадратных метров, можно уложить линолеум ЦЕЛЬНЫМ куском. Уже в марте сотрудники компании, не участвующие непосредственно в ПРОИЗВОДСТВЕННОМ процессе, были переведены на удалённый режим работы.
6. Отредактируйте предложение: исправьте лексическую ошибку, заменив неверно употреблённое слово. Запишите подобранное слово, соблюдая нормы современного русского литературного языка. Нередко за чудовище принимают гигантского осетра или же рой рыбы, который с берега кажется наблюдателю огромным змееподобным животным.
7. В одном из выделенных ниже слов допущена ошибка в образовании формы слова. Исправьте ошибку и запишите слово правильно.
- офицерских ПОГОН
- стая ЦАПЕЛЬ
- к ЧЕТЫРЁМСТАМ сорока саженцам
- килограмм ВАФЛЕЙ
- ПРИЙТИ вовремя
9. Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) бесш..рстный, ш..рох, реш..тка
- 2) вытр..хнутый (коврик), безм..тежность, прит..гательный
- 3) благоч..стивый, пренебр..жительно, выт..сненный (из толпы)
- 4) параш..тист, полуш..бок, ш..рупы
- 5) подр..стковый, уд..вольствие, провозгл..шать
10. Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) беспр..зорник, пр..ободриться, пр..скорбный (факт)
- 2) грузопод..ёмность, неот..емлемый, (нежданная) гост..я
- 3) о..дохнуть, по..толкнуть (к краю), пре..сказатель
- 4) вы..грать, от..мённое (прилагательное), сверхиз..сканный
- 5) ди..кредитация, не..говорчивый, обе..цветиться
11. Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) милост..вый, одерев..нелые (мышцы)
- 2) намер..ваться, запечатл..вать
- 3) ключ..вая (вода), ярко-оранж..вый
- 4) взрывч..тое (вещество), морщин..стый
- 5) пугов..чка, (по) старш..нству
12. Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- 1) (всё) перемел..тся, (он никак не) отдыш..тся
- 2) вымол..шь (пощаду), скрюч..вшийся (от боли)
- 3) обезглав..вший (гидру), (вы всегда) поддерж..те
- 4) раскач..нная (лодка), маяч..щий (вдали)
- 5) (они) бор..тся, (матрос) дра..щий (палубу)
13. Определите предложение, в котором НЕ с выделенным словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. Изобретение интернета – одно из самых ярких, но далеко (НЕ)ЕДИНСТВЕННОЕ в ряду сбывшихся предсказаний писателей. У Ивана был ещё другой мир, свой собственный, (НЕ)ДОСТУПНЫЙ абсолютно никому другому. Человечество (НЕ)ГОТОВО к безопасному использованию атомной энергии. (НЕ)МЕДЛЯ ни одного мгновения, истребитель поспешил на помощь несчастному товарищу. Говорил капитан (НЕ)ГРОМКО, но горячо, подтверждая каждое слово резкими движениями больших кулаков.
14. Определите предложение, в котором оба выделенных слова пишутся СЛИТНО. Раскройте скобки и выпишите эти два слова. Он посмотрел (НА)ВЕРХ противоположной стены, (ЗА)ТЕМ на небо и вспомнил то, что не мог вспомнить ночью. Ему поручили это ответственное дело (ПО)ТОМУ, что он лучше всех умел разбираться в горизонтах, движущихся точках и (В)ПРОЧЕМ подобном. (В)НАЧАЛЕ гастролей пианист пытался держать (В)ТАЙНЕ от близких свой отъезд. (ИЗ)ДАЛИ хищнику трудно понять, смотрит обезьяна в другую сторону или заметила его и сейчас стадо бросится (В)РАССЫПНУЮ. После долгих уговоров Осипов ВСЁ(ЖЕ) согласился отвести меня (В)МЕСТО особое, только ему известное – в арабский магазинчик, напоминающий лавку древностей.
15. Укажите цифру(-ы), на месте которой(-ых) пишется одна буква Н. Сочетание этих цветов соверше(1)о, а сами цвета изыска(2)ы и утончё(3)о чувстве(4)ы, поэтому невольно соглашаешься с мнением исти(5)ых ценителей искусства, восторже(6)о признавших картину лебеди(7)ой песней художника.
16. Расставьте недостающие знаки препинания. Укажите предложения, в которых нужно поставить ОДНУ запятую. Запишите номера этих предложений.
- 1) События и перемены происходили довольно редко и неожиданно и обычные дни теперь стали похожи друг на друга.
- 2) В скачках ракетного света речной лёд то приближался к ногам то стремительно соскальзывал нырял в потёмки.
- 3) Старые бытовые предметы начинают обозначать время через исторические или биографические события и становятся новыми символами привилегированного социального положения.
- 4) Всюду валялись обрезки дорогой купленной в Париже ткани и блестели рассыпанные стеклянные бусины и перламутровые пуговицы.
- 5) Расходы включают плату за проезд на рейсовом автобусе или поезде или же стоимость бензина для автомобиля.
17. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложении должна(-ы) стоять запятая(-ые). Козлята (1) ещё покрытые шелковистыми завитками (2) осторожно тянули из яслей зелёные былинки свежего сена (3) или (4) внезапно очнувшись от оцепенения (5) мягко стуча копытцами (6) по засыпанному опилками полу (7) и неловко взбрыкивая (8) неслись к выходу из амбара (9) сбивая всё на своём пути.
18. Расставьте все недостающие знаки препинания: укажите цифру(-ы), на месте которой(-ых) в предложениях должна(-ы) стоять запятая(-ые). После нас (1) разумеется (2) не потоп, но и не засуха. Скорей всего (3) климат в царстве справедливости будет носить характер умеренного, с четырьмя временами года, чтоб холерик, сангвиник, флегматик и меланхолик правили поочерёдно: на протяжении трёх месяцев каждый. С точки зрения энциклопедии (4) это – немало. Хотя (5) бесспорно (6) переменная облачность, капризы температуры могут смутить реформатора. Но бог торговли только радуется спросу на шерстяные вещи, английские зонтики, драповое пальто. Его злейшие недруги – штопаные носки и перелицованные жакеты. Казалось бы (7) дождь в окне поощряет (8) именно (9) этот подход к пейзажу и к материи в целом: как более экономный. (Иосиф Бродский)
19. Расставьте знаки препинания: укажите все цифры, на месте которых в предложении должны стоять запятые. В результате наблюдений за различными малыми небесными телами Солнечной системы (1) возникла новая теория (2) согласно которой (3) короткопериодические кометы в основном встречаются в регионе (4) чья внутренняя граница (5) частично перекрывается поясом Койпера (6) в то время как внешняя (7) находится на значительно большем расстоянии от Солнца.
20. Расставьте недостающие знаки препинания: укажите все цифры, на месте которых в предложении должны стоять запятые. Пока отходит наркоз (1) и стены палаты плывут перед глазами (2) я вслушиваюсь в громкие голоса за стеной (3) и (4) хотя чёткость восприятия в полной мере ещё не вернулась (5) упорно пытаюсь разобрать слова говорящих, осознавая с досадой (6) что из всего только что услышанного (7) я ничего не могу понять.
21. Найдите предложения, в которых запятая(-ые) ставится(-ятся) в соответствии с одним и тем же правилом пунктуации. Запишите номера этих предложений. (1)Александр Агеевич Абаза происходил из известного молдавского боярского рода, перешедшего на русскую службу ещё при императрице Анне Иоанновне. (2)Красавец и хитрец, он начал свою карьеру как храбрый лейбгусар. (3)Участвовал во многих сражениях на Кавказе и в 1847 году, в двадцать шесть лет, вышел майором в отставку «из-за болезни ран», однако ему было разрешено носить мундир. (4)Женившись на дочери богатейшего откупщика Александре Бенардаки, Абаза стал служить при дворе великой княгини Елены Павловны. (5)Он совмещал придворную службу с членством в ряде акционерных обществ, считался оборотистым дельцом и знатоком экономики. (6)В 1871 году стал государственным контролёром, а в 1880-м император назначил Александра Агеевича министром финансов. (7)В 1881 году пришедший к власти Александр III уволил его с министерской должности, зато Абаза занял важное место в департаменте государственной экономии. (8)Впрочем, и на этой должности он не задержался. (9)Несмотря на то что газета «Московские ведомости» и журнал «Гражданин» критиковали его за чрезмерное стремление к либеральным реформам, Александр Агеевич Абаза был избран почётным членом Императорской Санкт-Петербургской Академии Наук и позднее удостоен ордена Св. апостола Андрея Первозванного.
22. Какие из высказываний соответствуют содержанию текста? Укажите номера ответов.
- 1) Анна Вячеславовна была постоянной посетительницей комиссионного магазина.
- 2) Героиня была готова продать как можно больше вещей, чтобы создать «небольшой капитал на чёрный день».
- 3) Молодой человек пренебрёг тем, что автограф Симонова был ценен для пожилой женщины.
- 4) Героиня во время войны жила в блокадном Ленинграде.
- 5) Анна Вячеславовна боялась своего сына.
23. Какие из перечисленных утверждений являются верными? Укажите номера ответов.
- 1) В предложении 9 указана причина того, о чём говорится в предложении 8.
- 2) Предложение 14 содержит описание.
- 3) В предложениях 37, 38 представлено рассуждение.
- 4) В предложениях 66–69 представлено повествование.
- 5) Предложение 73 поясняет, раскрывает содержание предложения 72.
24. Из предложений 74–78 выпишите один фразеологизм.
25. Среди предложений 11–21 найдите такое(-ие), которое(-ые) связано(-ы) с предыдущим при помощи личного местоимения. Напишите номер(-а) этого(-их) предложения(-ий).
26. «Н.С. Литвинец создаёт образ доверчивой и беззащитной женщины, столкнувшейся с циничным миром, противостоять которому она не может. На языковом уровне это подчёркнуто с помощью такого приёма, как (А) (предложения 2, 48, 73). При этом писательница старается не навязывать читателю оценок изображаемого, поэтому будто бы сухо воспроизводит особую форму речи, такую как (Б) (39–40, 61–70). Речь и повествователя, и героев безыскусна, приближена к бытовой, поэтому мы почти не замечаем тропов, таких как (В) (“заставленные… хрусталём” в предложении 9) и (Г) (“накатывает усталость” в предложении 21, “мучила совесть” в предложении 73), что заставляет воспринять поведанную историю как часть нашей повседневной жизни, позволяет сделать трагедию героини близкой каждому читателю».
Текст ЕГЭ Литвинец Н.С
(1)Деньги кончились неожиданно. (2)Ещё вчера Анну Вячеславовну радовал приятный шорох купюр в видавшем виды портмоне, а сегодня она смогла обнаружить только мятую пятидесятирублёвку. (3)До пенсии оставалось больше недели.
(4)Она присела на диван и обвела взглядом гостиную. (5)Следовало чтото продать из содержимого большой, внушающей почтение горки. (6)Сын просил никогда этого не делать, сразу обращаться к нему, но Анна Вячеславовна была уверена, что он и не заметит отсутствия какой-нибудь изящной чашки.
(7)Анна Вячеславовна выбрала статуэтку давнишнего немецкого производства, потом отправилась в комиссионный магазин расположенный совсем недалеко. (8)Её ждало разочарование. (9)Словоохотливая владелица обвела рукой сплошь заставленные статуэтками и хрусталём полки, вздохнула и сказала, что взять что-то «в деньги» не получится, об этом не может быть и речи, только на комиссию, да и то неизвестно, когда всё это продастся, спрос в последнее время резко упал. (10)В утешение она дала Анне Вячеславовне телефон какого-то антиквара, который может купить всё за живые деньги, но, конечно, дешевле.
(11)Дома Анна Вячеславовна после некоторого раздумья набрала записанный номер. (12)Голос в телефонной трубке внушал доверие. (13)Он выслушал Анну Вячеславовну, записал адрес и пообещал подъехать сегодня же. (14)Антиквар оказался сравнительно молодым человеком, высоким, улыбчивым, приятной наружности, располагающим к себе. (15)«Ну, показывайте, что у вас тут есть», – по-хозяйски огляделся он. (16)Анна Вячеславовна показала статуэтку. (17)«А вот там и там у вас еще что?» – стал спрашивать тот. (18)Анна Вячеславовна заикнулась было, что ничего больше она продавать не собирается, ей бы только до пенсии дожить. (19)«А перед следующей пенсией снова мне позвоните? (20)Давайте создадим задел, чтоб у вас был небольшой капитал на чёрный день», – молодой человек звучал убедительно. (21)К тому же Анна Вячеславовна чувствовала, как на неё накатывает усталость, сил сопротивляться не было.
(22)«Вот за это всё – пятнадцать тысяч триста рублей, – сказал он. – (23)Я даю самую лучшую цену, спросите у кого хотите». (24)Чтобы немного выгадать время на размышление, Анна Вячеславовна предложила молодому человеку чаю.
(25)Пока они пили чай, она рассказывала ему свою жизнь. (26)Молодой человек слушал внимательно. (27)Хотелось вспоминать и вспоминать. (28)Молодой статный Алёша в ладно сидящей военной форме с боевыми наградами, поэт Константин Симонов с седыми висками и умными, немного грустными глазами, и рядом худенькая девчонка-блокадница. (29)«И что потом?» – спросил молодой человек. (30)«Алёша попросил его на книге расписаться. (31)А тот, как узнал, что его зовут Алёша, написал: (32)Ты, конечно, помнишь, Алёша, дороги войны… (33)Счастья тебе в мирной жизни! (34)На меня посмотрел и хитро так подмигнул». (35)Молодой человек заинтересовался. (36)«А увидеть автограф Симонова можно?» (37)Анна Вячеславовна достала тоненький ветхий сборник на жёлтой бумаге, старательно упакованный в пластиковый пакет, осторожно вынула и раскрыла первую страницу. (38)Молодой человек внимательно разглядывал симоновский автограф. (39)«Добавлю за это тысячу двести, всего будет шестнадцать с половиной», – произнёс он. (40)«Что вы, что вы, – замахала руками Анна Вячеславовна, – это не продаётся». (41)Молодой человек не стал настаивать.
(42)Он попросил пачку старых газет и принялся паковать вещи. (43)Анне Вячеславовне хотелось, чтобы он поскорее ушёл, и отчего-то было стыдно. (44)«Да, вы знаете, – сказал молодой человек. – у меня есть друг, он фанат Симонова, трясётся над каждой его строчкой. (45)Можно я возьму вашу книжечку на пару дней, другу покажу. (46)Через два дня верну. (47)Коллекционеры, они, знаете, сумасшедшие люди». (48)Анна Вячеславовна хотела отказать, но язык не повернулся. (49)Человек ведь действительно любит Симонова, ему важно этот автограф увидеть своими глазами. (50)Молодой человек расценил молчание как согласие и быстро сунул книжку в сумку.
(51)Через два дня он не появился. (52)На пятый день Анна Вячеславовна позвонила ему сама. (53)«Я в командировке, – ответил молодой человек. – (54)Приеду через два дня – и сразу к вам с книжкой». (55)После этого разговора прошла неделя. (56)Анна Вячеславовна позвонила ещё раз. (57)«Да-да, я всё помню, – ответил молодой человек. – (58)Завтра я у вас». (59)Так продолжалось с месяц. (60)В конце концов молодой человек предложил заменить утраченную книжку собранием сочинений Симонова. (61)«Ну как вы не понимаете, – чуть не плакала Анна Вячеславовна, – там же автограф Симонова. (62)Алёше. (63)Это для меня так важно». (64)Молодой человек помолчал в трубку. (65)«Это всего лишь книга, – сказал он. – (66)Стихи Симонова вы найдёте в любом другом издании, и в Интернете их полно. (67)А автограф, ну что автограф. (68)Всего лишь несколько слов, написанных давно умершим человеком. (69)У него даже могилы нет, прах по полю развеяли. (70)Ну, извините, так получилось». (71)После этого он перестал отвечать на звонки.
(72)Анна Вячеславовна прожила ужасный месяц. (73)Её мучила совесть, она чувствовала себя предательницей – по отношению к Алёше, к совместно прожитым счастливым годам, к совместно нажитым вещам, не представлявшим антикварной ценности, но таким дорогим им обоим. (74)Вскоре она слегла и больше уже не вставала. (75)Сын приехал проведать заболевшую мать и совершенно не заметил изрядно опустевшей горки. (76)А про автограф Симонова Анна Вячеславовна сказать ему побоялась. (77)Это ему знать ни к чему. (78)Это касалось только её и Алёши, с которым ей скоро предстояло увидеться.
По Н.С. Литвинец
*Нина Сергеевна Литвинец (род. в 1947 г.) – российская писательница, литературовед, переводчик.
Попробуйте решить другие варианты
Русский язык 11 класс 2210401-2210402 статград варианты и ответы ЕГЭ 2023