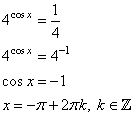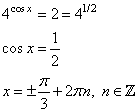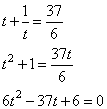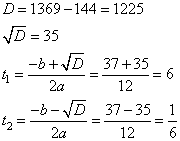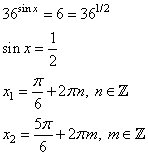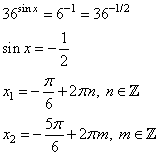31 декабря 2014 года Никита взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Никита переводит очередной транш. Если он будет платить каждый год по 2 073 600 рублей, то выплатит долг за 4 года. Если по 3 513 600 рублей, то за 2 года. Под какой процент Никита взял деньги в банке?
Спрятать решение
Решение.
Пусть S — сумма кредита. Обозначим ежегодные платежи и
соответственно. Сумма долга каждый год увеличивается на
то есть сумма долга умножается на коэффициент
После первой выплаты сумма долга станет равной
после второй выплаты:
после третье выплаты:
после четвёртой выплаты:
Причём долг будет погашен полностью, получаем, то есть
Аналогично получаем уравнение для случая, когда выплаты совершаются платежами размером
Имеем систему уравнений:
Подставим выражение для в первое уравнение:
Преобразуем это уравнение:
Подставляя числовые значения получаем:
Отрицательные корни не подходят по условию задачи, значит, откуда
то есть Никита взял деньги в банке под 20%.
Ответ: 20%.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Версия для печати и копирования в MS Word
1
31 декабря 2014 года Никита взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Никита переводит очередной транш. Если он будет платить каждый год по 2 073 600 рублей, то выплатит долг за 4 года. Если по 3 513 600 рублей, то за 2 года. Под какой процент Никита взял деньги в банке?
2
31 декабря 2014 года Олег взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Олег переводит очередной транш. Если он будет платить каждый год по 328 050 рублей, то выплатит долг за 4 года. Если по 587 250 рублей, то за 2 года. Найдите а.
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2017. Задания С5., Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 2. (Часть C).
3
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 75 000 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 123 000 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 302 (C часть).
4
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
− каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть).
5
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 77 760 руб, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 131 760 руб, то кредит будет полностью погашен за 2 года. Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 303 (C часть).
6
В августе 2020 года взяли кредит. Условия возврата таковы:
— каждый год в декабре долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за четыре года равными платежами по 56 507 рублей, или за два года равными платежами по 103 207 рублей.
Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017
7
В августе 2020 года взяли кредит. Условия возврата таковы:
— в январе каждого года долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за четыре года равными платежами по 777 600 рублей, или за два года равными платежами по 1 317 600 рублей.
Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
а) Решите уравнение cos2x = 1-cos(п/2-x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п].
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие тригонометрические уравнения.
Пункт б)
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
Пункт а)
1. Преобразуем правую часть равенства, используя формулу приведения cos(π/2−x)=sinx. Имеем:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
cos(2х)=1−2sin2 х
Получаем такое уравнение: 1−sin 2x=1− sinx
Теперь в уравнении присутствует только одна тригонометрическая функция sinx.
2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
1−2t2=1−t,
−2t2+t=0,
t (−2t+1)=0,
t = 0 или -2t + 1 = 0,
t1 = 0 t2 = 1/2.
3. Делаем обратную замену:
sin x = 0 или sin x = ½
Решаем эти уравнения:
sin x =0↔x=πn, nЄZ
sin(x)=1/2↔x= (-1)n∙(π/6)+ πn, nЄZ.
Следовательно, получаем два семейства решений.
Пункт б):
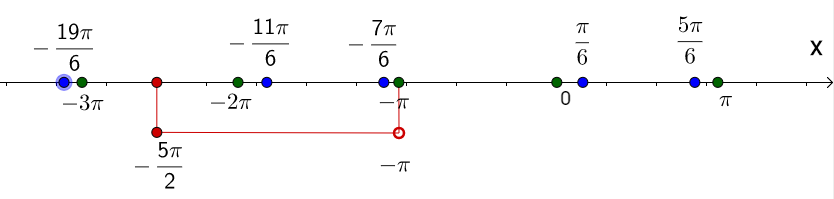
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
3. Красным цветом помечаем концы промежутка.
4. В указанном промежутке расположены три корня что три корня: −2π;−11π/6 и −7π/6.
Ответ:
а) πn, nЄZ; (-1)n∙(π/6)+ πn, nЄZ
б) −2π;−11π6;−7π6
Второй вариант задания (из Ященко, №1)
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Алгоритм решения:
Пункт а)
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
Пункт б)
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Пункт а)
1. Вводим замену t = 4cos х. тогда уравнение примет вид:
Решаем квадратное уравнение с помощью формул дискриминанта и корней:
D=b2 – c = 81 – 4∙4∙2 =49,
t1= (9 – 7)/8= ¼, t2 = (9+7)/8=2.
3. Возвращаемся к переменной х:
Пункт б)
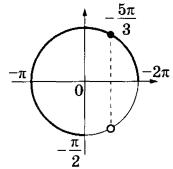
1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка..
Это корни . Их два.
Ответ:
а)
б)
Третий вариант задания (из Ященко, № 6)
а) Решите уравнение 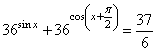
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
Пункт б)
- Решаем неравенства для каждого случая.
- Записываем ответ.
Решение:
а)
1. По формулам приведения .
2. Тогда данное уравнение примет вид:
3. Вводим замену . Получаем:
Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней:
Оба корня положительны.
3. Возвращаемся к переменной х:
Получили четыре семейства корней. Их бесконечно много.
б)
4. С помощью неравенств находим те корни, которые принадлежащие отрезку :
Для корней
Получаем одно значение .
Для корней
ни одного значения корней нет.
Для корней
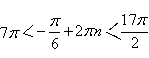
;
Для корней
есть одно значение
.
Ответ:
а) ;
;
б) .
Вариант ХИ2210401 с ответами
Скачать ответы и
решения для варианта
Для выполнения заданий 1–3 используйте следующий ряд
химических элементов:
●
1) Mg,
●
2) C,
●
3) B,
●
4) Si, ● 5) Li.
Ответом в заданиях 1–3 является последовательность
цифр, под которыми указаны химические элементы в данном ряду.
1.
Какие из указанных элементов имеют в первом возбуждённомсостоянии
конфигурацию внешнего уровня ns1 np3 ? Запишите номера выбранных элементов.
2.
Из указанного ряда выберите три элемента, принадлежащие
одномупериоду Периодической системы, и расположите их в порядке увеличения
первой энергии ионизации атома. Запишите в поле ответа номера выбранных
элементов в нужной последовательности.
3.
Из указанного ряда выберите два элемента, у которых разностьмежду
высшей и низшей степенями окисления равна 8. Запишите в поле ответа номера
выбранных элементов.
4.
Из предложенного перечня выберите две частицы, в которых одиниз
элементов образует четыре ковалентные связи. Запишите номера выбранных ответов.
●
1) NH3
●
2) H2O2
●
3) BF4 –
●
4) P4O6
●
5) SO2
5.
Среди предложенных формул/названий веществ, расположенных
впронумерованных ячейках, выберите формулы/названия: А) сильного основания; Б)
основной соли; В) одноосновной кислоты. Запишите в таблицу номера ячеек, в
которых расположены вещества, под соответствующими буквами.
6.
В двух пробирках находился раствор карбоната аммония. В
первуюпробирку добавили раствор вещества Х, а во вторую – раствор вещества Y. В
первой пробирке видимых признаков реакции не наблюдалось даже при нагревании, а
во второй выпал желтоватый осадок. Из предложенного перечня выберите вещества X
и Y, которые могут вступать в описанные реакции.
●
1) NaOH
●
2) CaCl2
●
3) AgNO3
●
4) K2SO4
●
5) CuSO4
7.
Установите соответствие между формулой вещества и реагентами,
скаждым из которых это вещество может взаимодействовать: к каждой позиции,
обозначенной буквой, подберите соответствующую позицию, обозначенную цифрой.
8.
Установите соответствие между исходными веществами,вступающими в
реакцию, и продуктами, которые образуются при взаимодействии этих веществ: к
каждой позиции, обозначенной буквой, подберите соответствующую позицию,
обозначенную цифрой.
10.
Установите соответствие между названием гомологического ряда иего
общей формулой: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
11.
Из предложенного перечня выберите два межклассовых
изомера.Запишите номера выбранных ответов.
●
1) пентанон-3 ● 2)
пентанол-1
●
3) 3-метилбутанон
●
4) пентановая кислота
●
5) этилизопропиловый эфир
12.
Из предложенного перечня выберите все вещества, которые приопределённых
условиях могут быть восстановлены до первичного спирта. Запишите номера
выбранных ответов.
●
1) ацетон
●
2) масляная кислота
●
3) фенол
●
4) этилацетат
●
5) 2-метилпропаналь
13.
Из предложенного перечня выберите два вещества, которыепроявляют
более сильные основные свойства, чем аммиак. Запишите номера выбранных ответов.
●
1) нитробензол
●
2) 1,2-диаминоэтан
●
3) анилин
●
4) пиридин
●
5) диметиламин
14.
Установите соответствие между схемой реакции и веществом
Х,принимающим в ней участие: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
15.
Установите соответствие между реагирующими веществами
иуглеродсодержащим продуктом, который образуется при взаимодействии этих
веществ: к каждой позиции, обозначенной буквой, подберите соответствующую
позицию, обозначенную цифрой.
17. Из
предложенного перечня выберите все реакции присоединения.Запишите номера
выбранных ответов.
●
1) взаимодействие хлорэтана со спиртовым раствором щёлочи
●
2) взаимодействие циклопропана с бромом
●
3) взаимодействие пентана с бромом на свету
●
4) взаимодействие бутадиена с хлороводородом
●
5) димеризация ацетилена в присутствии катализатора
18. Из
предложенного перечня выберите все реакции, скоростькоторых зависит от
давления. Запишите номера выбранных ответов.
●
1) взаимодействие хлора с раствором щёлочи
●
2) растворение железа в соляной кислоте
●
3) восстановление оксида меди(II) водородом
●
4) нитрование бензола
●
5) горение алюминия в кислороде
19. Установите
соответствие между схемойокислительно-восстановительной реакции и степенью
окисления элемента-восстановителя: к каждой позиции, обозначенной буквой,
подберите соответствующую позицию, обозначенную цифрой.
20. Установите
соответствие между формулой вещества и продуктамиэлектролиза водного раствора
или расплава этого вещества, выделившимися на инертных электродах: к каждой
позиции, обозначенной буквой, подберите соответствующую позицию, обозначенную
цифрой.
21. Для
веществ, приведённых в перечне, определите характер средыих водных растворов,
имеющих одинаковую молярную концентрацию. Запишите номера веществ в порядке
возрастания значения pH их водных растворов.
●
1) K2SO4
●
2) K2SO3
●
3) KHSO4
●
4) K2S
22. Установите
соответствие между способом воздействия наравновесную систему CO3 2– (р-р) +
H2O(ж.) HCO3 – (р-р) + OH– (р-р) – Q и направлением смещения равновесия при
этом воздействии: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
23. В реакторе
постоянного объёма смешали азот и водород. Врезультате обратимой реакции: N2(г)
+ 3H2(г) ←→ 2NH3(г) в реакторе установилось равновесие. Исходная концентрация
азота была равна
1,0 моль/л, а равновесные концентрации водорода и
аммиака составили 2,0 моль/л и 0,8 моль/л, соответственно. Найдите равновесную
концентрацию азота (X) и исходную концентрацию водорода (Y). Выберите из списка
номера правильных ответов.
●
1) 0,4 моль/л
●
2) 0,6 моль/л
●
3) 0,8 моль/л
●
4) 1,2 моль/л
●
5) 2,4 моль/л
●
6) 3,2 моль/л
24. Установите
соответствие между названием вещества и признакомреакции, который наблюдается
при взаимодействии вещества с водным раствором аммиака: к каждой позиции,
обозначенной буквой, подберите соответствующую позицию, обозначенную цифрой.
25. Установите
соответствие между смесью веществ и методом еёразделения: к каждой позиции,
обозначенной буквой, подберите соответствующую позицию, обозначенную цифрой.
26. При
охлаждении 200 г раствора гидрокарбоната аммония выпалосадок – безводная соль.
Раствор над осадком имел массу 150 г и содержал 18 % соли по массе. Найдите
массовую долю (в %) соли в исходном растворе. (Запишите число с точностью до
десятых.)
27. Горение
угарного газа описывается термохимическим уравнением: CO(г) + 1/2O2(г) = CO2(г)
+ 284 кДж Сколько литров кислорода (н. у.) потребуется для получения 213 кДж
теплоты сжиганием угарного газа? (Запишите число с точностью до десятых.)
28. Сколько
килограммов бутадиена-1,3 можно получить из 20 кг 96 %-го этанола, если выход в
реакции Лебедева составляет 71 %? (Ответ запишите с точностью до целых.)
29. Из предложенного
перечня выберите вещества, между которымиокислительно-восстановительная реакция
протекает с изменением цвета раствора. В ответе запишите уравнение только одной
из возможных окислительновосстановительных реакций с участием выбранных
веществ. Составьте электронный баланс, укажите окислитель и восстановитель.
30. Из
предложенного перечня веществ выберите вещества, которыевступают в реакцию
ионного обмена с выделением газа. Запишите молекулярное, полное и сокращённое
ионное уравнения реакции с участием выбранных веществ.
31. Серебро
растворили в разбавленной азотной кислоте. Черезполученный раствор пропустили
сероводород, из раствора выпал чёрный осадок. Осадок отфильтровали и прокалили
на воздухе. Газ, выделившийся при прокаливании, поглотили известковой водой, в
результате из раствора выпал осадок. Напишите молекулярные уравнения четырёх
описанных реакций.
32. Напишите
уравнения реакций, с помощью которых можноосуществить следующие превращения:
С3H6 → C3H6Br2 → X1 → пропандиовая кислота → X2 → C2H3OCl При написании
уравнений реакций указывайте преимущественно образующиеся продукты, используйте
структурные формулы органических веществ.
33. Органическое
вещество X относится к ароматическим соединениям и проявляет слабые основные
свойства. Оно реагирует с одним эквивалентом хлороводорода, образуя вещество,
содержащее 27,4 % хлора и 10,8 % азота по массе. Вещество X окисляется
перманганатом калия, не реагирует с бромной водой и азотистой кислотой. На
основании данных условия задачи: 1) проведите необходимые вычисления
(указывайте единицы измерения и обозначения искомых физических величин) и
установите молекулярную формулу вещества X; 2) составьте возможную структурную
формулу вещества X, которая однозначно отражает порядок связи атомов в его
молекуле; 3) напишите уравнение реакции вещества X с горячим водным раствором
перманганата калия (в уравнении используйте структурные формулы органических
веществ).
34. Навеску хлорида
фосфора(V) растворили в 50 мл горячей воды.
Для полной нейтрализации полученного раствора
потребовалось 190 г
3,6 %-го раствора гидроксида
бария. Выпавший осадок отфильтровали. Рассчитайте массу осадка и массовую долю
соли в фильтрате. В ответе запишите уравнения реакций, которые указаны в
условии задачи, и приведите все необходимые вычисления (указывайте единицы
измерения и обозначения искомых физических величин).
Вариант ХИ2210402 с ответами
Для выполнения заданий 1–3 используйте следующий ряд
химических элементов: 1) Na, 2) O, 3) Ar, 4) B, 5) Al Ответом в заданиях 1–3
является последовательность цифр, под которыми указаны химические элементы в
данном ряду.
1.
Какие из указанных элементов имеют в первом возбуждённомсостоянии
конфигурацию внешнего уровня ns1 np2 ? Запишите номера выбранных элементов.
2.
Из указанного ряда выберите три элемента, принадлежащие
одномупериоду Периодической системы, и расположите их в порядке уменьшения
первой энергии ионизации атома. Запишите в поле ответа номера выбранных
элементов в нужной последовательности.
3.
Из указанного ряда выберите два элемента, способные
проявлятьотрицательную степень окисления. Запишите в поле ответа номера
выбранных элементов.
4.
Из предложенного перечня выберите две частицы, в которых одиниз
элементов образует три ковалентные связи. Запишите номера выбранных ответов.
●
1) NH4 +
●
2) SO3
●
3) AlH4 –
●
4) H3O+
●
5) HCN
5.
Среди предложенных формул/названий веществ, расположенных
впронумерованных ячейках, выберите формулы/названия: А) основного оксида; Б)
бескислородной кислоты; В) кислой соли. Запишите в таблицу номера ячеек, в
которых расположены вещества, под соответствующими буквами.
6.
В двух пробирках находился раствор иодида алюминия. В
первуюпробирку добавили раствор вещества Х, а во вторую – раствор вещества Y. В
первой пробирке видимых признаков реакции не наблюдалось, а во второй выпал
белый осадок, при этом газ не выделялся. Из предложенного перечня выберите
вещества X и Y, которые могут вступать в описанные реакции.
●
1) NH4Cl
●
2) Pb(NO3)2
●
3) K2CO3
●
4) NH3
●
5) (NH4)2S
7.
Установите соответствие между формулой вещества и реагентами,
скаждым из которых это вещество может взаимодействовать: к каждой позиции,
обозначенной буквой, подберите соответствующую позицию, обозначенную цифрой.
8.
Установите соответствие между исходными веществами,вступающими в
реакцию, и продуктами, которые образуются при взаимодействии этих веществ: к
каждой позиции, обозначенной буквой, подберите соответствующую позицию,
обозначенную цифрой.
10.
Установите соответствие между названием гомологического ряда иего
общей формулой: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
11.
Из предложенного перечня выберите два структурных
изомера.Запишите номера выбранных ответов.
●
1) пентандиол-2,3
●
2) пропилацетат
●
3) дипропиловый эфир
●
4) циклопентанол
●
5) 2-метилбутаналь
12.
Из предложенного перечня выберите все вещества, при
гидролизекоторых в кислой среде образуется карбоновая кислота. Запишите номера
выбранных ответов.
●
1) 2,2-дихлопропан
●
2) уксусный ангидрид
●
3) 1,1,1-трихлорэтан
●
4) цианометан
●
5) метоксибензол
13.
Из предложенного перечня выберите два вещества, которыепроявляют
основные свойства, но являются более слабыми основаниями, чем аммиак. Запишите
номера выбранных ответов.
●
1) пиррол
●
2) пиридин
●
3) триметиламин
●
4) метилат натрия
●
5) 2-метиланилин
14.
Установите соответствие между схемой реакции и веществом
Х,принимающим в ней участие: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
15.
Установите соответствие между реагирующими веществами
иорганическим продуктом, который преимущественно образуется при взаимодействии
этих веществ: к каждой позиции, обозначенной буквой, подберите соответствующую
позицию, обозначенную цифрой.
17.
Из предложенного перечня выберите все реакции замещения.Запишите
номера выбранных ответов.
●
1) взаимодействие 2-хлорпропана с водным раствором щёлочи
●
2) взаимодействие фенола с разбавленной азотной кислотой
●
3) нагревание 1,3-дибромпропана с цинком
●
4) взаимодействие ацетона с водородом
●
5) взаимодействие метиламина с хлорметаном
18.
Из предложенного перечня выберите все реакции, скоростькоторых не
зависит от давления. Запишите номера выбранных ответов.
●
1) горение серы в кислороде
●
2) растворение алюминия в растворе щёлочи
●
3) нейтрализация азотной кислоты гидроксидом бария
●
4) изомеризация α-глюкозы в β-глюкозу
●
5) взаимодействие аммиака и хлороводорода
19.
Установите соответствие между
схемойокислительно-восстановительной реакции и степенью окисления
элемента-окислителя: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
20.
Установите соответствие между формулой вещества и
продуктамиэлектролиза водного раствора или расплава этого вещества,
выделившимися на инертных электродах: к каждой позиции, обозначенной буквой,
подберите соответствующую позицию, обозначенную цифрой.
21.
Для веществ, приведённых в перечне, определите характер средыих
водных растворов, имеющих одинаковую концентрацию (моль/л). Запишите номера
веществ в порядке уменьшения значения pH их водных растворов.
●
1) NaHCO3
●
2) NaI
●
3) NaOH
●
4) HI
23.
В реакторе постоянного объёма смешали оксид серы(IV) и кислород.
В результате обратимой реакции: 2SO2(г) + O2(г) ←→ 2SO3(г) в реакторе
установилось равновесие. Исходная концентрация кислорода была равна 0,1 моль/л,
а равновесные концентрации оксида серы(VI) и оксида серы(IV) составили 0,08
моль/л и 0,12 моль/л, соответственно. Найдите равновесную концентрацию
кислорода (X) и исходную концентрацию оксида серы(IV) (Y). Выберите из списка
номера правильных ответов.
●
1) 0,04 моль/л
●
2) 0,06 моль/л
●
3) 0,08 моль/л
●
4) 0,12 моль/л
●
5) 0,16 моль/л
●
6) 0,2 моль/л
24.
Установите соответствие между названием вещества и
признакомреакции, который наблюдается при взаимодействии вещества с
разбавленной соляной кислотой: к каждой позиции, обозначенной буквой, подберите
соответствующую позицию, обозначенную цифрой.
25.
Установите соответствие между смесью веществ и методом
еёразделения: к каждой позиции, обозначенной буквой, подберите соответствующую
позицию, обозначенную цифрой.
26.
При охлаждении 400 г 70 %-го раствора нитрата аммония выпалосадок
– безводная соль. В образовавшемся растворе массовая доля нитрата аммония
снизилась до 60 %. Найдите массу осадка (в г). (Запишите число с точностью до
целых.)
27.
Горение бутана описывается термохимическим уравнением: C4H10(г) +
6,5O2(г) = 4CO2(г) + 5H2O(ж) + 2880 кДж Сколько миллилитров углекислого газа
(н.у.) выделится в атмосферу при получении 360 Дж теплоты сжиганием бутана?
(Ответ запишите с точностью до десятых).
28.
В результате тримеризации пропина объёмом 74 л (н. у.)
получилисмесь триметилбензолов общей массой 99 г. Рассчитайте общий выход (в %)
продуктов тримеризации. (Ответ запишите с точностью до целых.)
29.
Из предложенного перечня выберите вещества, между
которымиокислительно-восстановительная реакция протекает с выделением газа и
изменением цвета раствора. В ответе запишите уравнение только одной из
возможных окислительновосстановительных реакций с участием выбранных веществ.
Составьте электронный баланс, укажите окислитель и восстановитель.
30.
Из предложенного перечня веществ выберите вещества,
которыевступают в реакцию ионного обмена с образованием осадка. Запишите
молекулярное, полное и сокращённое ионное уравнения реакции с участием
выбранных веществ.
31.
Чёрное вещество, образовавшееся при прокаливании нитрата
меди,растворили в соляной кислоте. Через полученный раствор пропустили
сернистый газ, в результате выпал белый осадок, который растворяется в
аммиачной воде. Напишите молекулярные уравнения четырёх описанных реакций.
32.
Напишите уравнения реакций, с помощью которых можноосуществить
следующие превращения: C4H10O → бутен-2 → X1 → бутин-2 → X2 → C12H6O12 При
написании уравнений реакций указывайте преимущественно образующиеся продукты,
используйте структурные формулы органических веществ.
33.
Органическое вещество X представляет собой бесцветную жидкость с
запахом аммиака. Оно реагирует с двумя эквивалентами бромоводорода, образуя
вещество, содержащее 72,1 % брома и 12,6 % азота по массе. Вещество X реагирует
с азотистой кислотой, при этом выделяется в 2 раза больше азота, чем при
сгорании X. На основании данных условия задачи:
●
1) проведите необходимые вычисления (указывайте единицы измерения
и обозначения искомых физических величин) и установите молекулярную формулу
вещества X;
●
2) составьте структурную формулу вещества X, которая однозначно
отражает порядок связи атомов в его молекуле;
●
3) напишите уравнение реакции вещества X с избытком гидроксида
калия (в уравнении используйте структурные формулы органических веществ).
34.
Для полной нейтрализации раствора, полученноговзаимодействием
хлорангидрида серной кислоты SO2Cl2 со 100 мл горячей воды, потребовалось 380 г
2,7 %-го раствора гидроксида бария. Выпавший осадок отфильтровали. Рассчитайте
массу осадка и массовую долю соли в фильтрате. В ответе запишите уравнения
реакций, которые указаны в условии задачи, и приведите все необходимые
вычисления (указывайте единицы измерения и обозначения искомых физических
величин).
Скачать ответы и
решения для варианта
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 14 № 508380
Воспользуемся тем, что для суммы возможны четыре случая раскрытия модулей, откуда заключаем:
Приведем другое решение:
Как и в первом решении запишем неравенство в виде:
Заметим, что левая часть представляет из себя кусочно-линейную функцию, которая возрастает при и убывает при Это означает, что в точке –3 она достигает минимума равного 5. Таким образом, правая часть Тогда неравенство принимает вид:
Задание 14 № 508380
—>
508780 решу егэ математика.
Ege. sdamgia. ru
07.03.2017 0:00:13
2017-03-07 00:00:13
Источники:
Https://ege. sdamgia. ru/problem? id=508380
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4~орла»?
Задание 10 № 508782
Симметричную монету бросают 12 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5~орлов»?
Задание 10 № 508783
Симметричную монету бросают 8 раз. Во сколько раз вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508784
Симметричную монету бросают 9 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508785
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 4 орла» больше вероятности события «выпадет ровно 3~орла»?
Задание 10 № 508786
Симметричную монету бросают 16 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508787
Симметричную монету бросают 17 раз. Во сколько раз вероятность события «выпадет ровно 8 орлов» больше вероятности события «выпадет ровно 7~орлов»?
Задание 10 № 508788
Симметричную монету бросают 20 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508789
Симметричную монету бросают 21 раз. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508790
Симметричную монету бросают 22 раза. Во сколько раз вероятность события «выпадет ровно 10 орлов» больше вероятности события «выпадет ровно 9~орлов»?
Задание 10 № 508786
Задание 10 № 508781
Задание 10 508786.
Ege. sdamgia. ru
14.05.2019 20:28:53
2019-05-14 20:28:53
Источники:
Https://ege. sdamgia. ru/test? likes=508780
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 508780 решу егэ математика
508780 решу егэ математика
508780 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 10 № 508780
Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Воспользуемся формулой Бернулли. Найдем вероятность события А, состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:
Аналогично найдем вероятность события B, состоящего в том, что при десяти бросаниях выпадет ровно 4 орла:
Приведем решение Ирины Шраго.
Вероятность того, что выпадет ровно 5 орлов, равна отношению количества вариантов, при которых выпадает ровно 5 орлов, к общему количеству вариантов: Вероятность того, что выпадет ровно 4 орла, равна отношению количества вариантов, при которых выпадает ровно 4 орла, к общему количеству вариантов: Тогда отношение этих вероятностей
—>
Задание 10 № 508780
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
09.08.2017 16:57:34
2017-08-09 16:57:34
Источники:
Https://ege. sdamgia. ru/problem? id=508780
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Решение и ответы заданий демонстрационного варианта ВПР 5 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Выполните сложение:
frac{2}{7}+frac{3}{7}
ИЛИ
Представьте в виде обыкновенной дроби число 2frac{3}{8}.
Задание 2.
Найдите наибольшее из чисел:
9,8 10,14 10,3 9,4
Задание 3.
В автобусе 51 место для пассажиров. Две трети мест уже заняты. Сколько свободных мест в автобусе?
Задание 4.
Каким числом нужно заменить букву А, чтобы получилось верное равенство?
А : 31 = 26
Задание 5.
Принтер печатает 72 страницы за 3 минуты. За сколько минут этот принтер напечатает 120 страниц?
Запишите решение и ответ.
Задание 6.
Найдите значение выражения 4800:24 − 4⋅(81− 63):2. Запишите решение и ответ.
Задание 7.
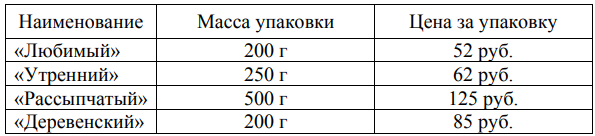
В магазине продаётся несколько видов творога в различных упаковках и по различной цене. В таблице показана масса каждой упаковки и её цена. Определите, килограмм какого творога стоит дешевле других. В ответ запишите стоимость одного килограмма этого творога.
Запишите решение и ответ.
Задание 8.
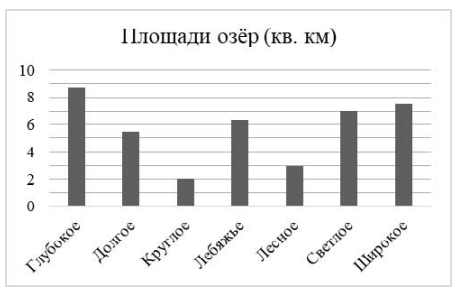
На диаграмме представлены площади нескольких озёр. Ответьте на вопросы.
1) Какое из этих озер занимает пятое место по площади?
2) На сколько квадратных километров площадь озера Светлое больше площади озера Лесное?
Задание 9.
Из одинаковых кубиков сложили параллелепипед (рис. 1). После этого сверху вытащили ровно один кубик (рис. 2).
Сколько кубиков осталось в фигуре, изображённой на рис. 2?
Задание 10.
В одном из районов города кварталы имеют форму квадратов со стороной 100 м. Ширина всех улиц равна 30 м.
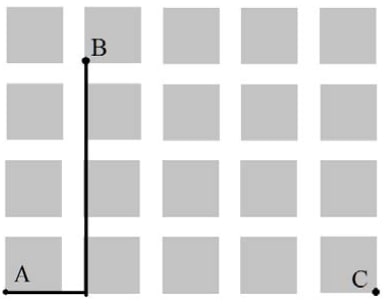
2) Нарисуйте на плане какой-нибудь маршрут, который начинается и заканчивается в точке С и имеет протяжённость не меньше 1 км, но не больше 1 км 200 м.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.