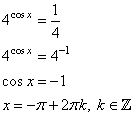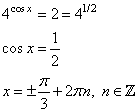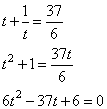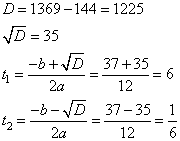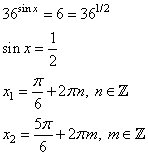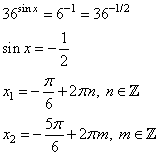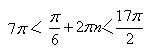Решу егэ 507788 - Помощь в подготовке к экзаменам и поступлению

Сторона основания правильной треугольной призмы ABCA₁B₁C₁ равна 8. Высота этой призмы равна 6.

а)  Докажите, что плоскость, содержащая прямую AB₁ и параллельная прямой CA₁ проходит через середину ребра BC.

б)  Найти угол между прямыми CA₁ и AB₁.

Спрятать решение

Решение.

Достроим треугольную прямую призму до четырехугольной прямой призмы, в основании которой ромб ABDC, составленный из двух равносторонних треугольников.

Полученная призма является прямым параллелепипедом. Поэтому

а)  Плоскость AB_1D параллельна прямой A_1C по признаку параллельности. Диагонали ромба ABDС пересекают друг друга посередине, поэтому плоскость AB_1D проходит через середину ребра BC.

б)   значит, искомый угол AB_1D. Рассмотрим ромб ABDC: площадь ромба равна произведению квадрата его стороны на синус угла ромба С другой стороны, площадь ромба можно найти как полупроизведение длин его диагоналей: следовательно,

Из прямоугольного треугольника AA_1B_1 по теореме Пифагора находим: Аналогично, Значит, из равнобедренного треугольника

AB_1D, получаем

Примечание 1.

Диагональ ромба можно было найти по теореме косинусов для треугольника ABD.

Примечание 2.

Для нахождения угла AB_1D можно применить в треугольнике AB_1D теорему косинусов:

откуда

Ответ: или

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен	1
Решение не соответствует ни одному из критериев, приведённых выше	0
Максимальный балл	3

Источник

На какие числа делится число онлайн калькулятор. Посчитать делители числа.

Какие числа делятся на 507788?

На число 507788 без остатка (нацело) делятся следующие числа: 507788, 1015576, 1523364, 2031152, 2538940, 3046728, 3554516, 4062304, 4570092, 5077880, 5585668, 6093456 и многие другие.

Какие четные числа делятся на 507788?

На число 507788 делятся следующие четные числа: 507788, 1015576, 1523364, 2031152, 2538940, 3046728, 3554516, 4062304, 4570092, 5077880, 5585668, 6093456 и многие други.

Какие нечетные числа делятся на 507788?

Таких чисел нет

На какое наибольшее число делится число 507788 без остатка?

Наибольшее число на которое делится число 507788 есть само число 507788. т.е делиться на само себя без остатка.

На какое наибольшее число делится число 507788 без остатка, не считая числа 507788 и 1?

Наибольшим делителем числа 507788 не считая самого числа 507788 является число 253894.

Какое наименьшее натуральное число делится на 507788?

Наименьшее натуральное число которое делиться на число 507788 является само число 507788.

На какое наименьшее натуральное число делится число 507788?

Наименьшее натуральное число на которое можно разделить число 507788 — это число 1.

Делители числа 507788.

(что бы не забыть запишите все делители числа 507788 в блокнот.)На какие целые и(или) натуральные числа делится число 507788?

Число 507788 делится на следующие целые, натуральные числа (все делители числа 507788): 1, 2, 4, 37, 47, 73, 74, 94, 146, 148, 188, 292, 1739, 2701, 3431, 3478, 5402, 6862, 6956, 10804, 13724, 126947, 253894, 507788

На какие четные числа делится число 507788?

Число 507788 делится на следующие четные числа (четные делители числа): 2, 4, 74, 94, 146, 148, 188, 292, 3478, 5402, 6862, 6956, 10804, 13724, 253894, 507788

На какие нечетные числа делится число 507788?

Число 507788 делится на следующие нечетные числа (нечетные делители числа): 1, 37, 47, 73, 1739, 2701, 3431, 126947

Сколько делителей имеет число 507788?

Число 507788 имеет 24 делителя

Сколько четных делителей имеет число 507788?

Число 507788 имеет 16 четных делителей

Сколько нечетных делителей имеет число 507788?

Число 507788 имеет 8 нечетных делителей

Число 507788 прописью, словами.

— пятьсот семь тысяч семьсот восемьдесят восемь

(что бы не забыть запишите число 507788 прописью в блокнот.)

Числа кратные 507788.

— кратные числа, числу 507788 : 1015576, 1523364, 2031152, 2538940, 3046728, 3554516, 4062304, 4570092, 5077880, 5585668, 6093456 и многие другие.

Простые множители числа 507788.

У числа 507788 нет простых множителей кроме 1.

Сумма цифр числа 507788.

Сумма цифр числа 507788 равна 35

Произведение цифр числа 507788.

Произведение цифр числа 507788 равна 0

Квадрат числа 507788.

Квадрат числа 507788 равен 257848652944

Куб числа 507788.

Куб числа 507788 равен 130932451781127872

Квадратный корень числа 507788.

Квадратный корень числа 507788 равен 712.5924.

Число 507788 в двоичной системе счисления.

Запись числа 507788 в двоичной системе счисления выглядит так: 1111011111110001100

Количество значащих нулей в двоичной записи числа 507788 = 6

Количество едениц в двоичной записи числа 507788 = 13

(что бы не забыть запишите число 507788 в двоичной системе счисления в блокнот.)Число 507788 в шестнадцатеричной системе счисления.

Запись числа 507788 в шестнадцатеричной системе счисления выглядит так: 7bf8c

(что бы не забыть запишите число 507788 в шестнадцатеричной системе счисления в блокнот.)Число 507788 в восьмеричной системе счисления.

Запись числа 507788 в восьмеричной системе счисления выглядит так: 1737614

(что бы не забыть запишите число 507788 в восьмеричной системе счисления в блокнот.)Число 507788 не является простым!

Корни числа 507788.

Корень 3 степени из 507788.

Корень 3 (третьей) степени из 507788 равен 79.780020668096

Корень 4 степени из 507788.

Корень 4 (четвертой) степени из 507788 равен 26.69442732374

Корень 5 степени из 507788.

Корень 5 (пятой) степени из 507788 равен 13.840012637794

Корень 6 степени из 507788.

Корень 6 (шестой) степени из 507788 равен 8.9319662263186

Корень 7 степени из 507788.

Корень 7 (седьмой) степени из 507788 равен 6.5327718395307

Корень 8 степени из 507788.

Корень 8 (восьмой) степени из 507788 равен 5.166665009824

Корень 9 степени из 507788.

Корень 9 (девятой) степени из 507788 равен 4.3049163286922

Корень 10 степени из 507788.

Корень 10 (десятой) степени из 507788 равен 3.7202167460773

Корень 11 степени из 507788.

Корень 11 (одиннадцатой) степени из 507788 равен 3.3014019467396

Корень 12 степени из 507788.

Корень 12 (двенадцатой) степени из 507788 равен 2.9886395276645

Корень 13 степени из 507788.

Корень 13 (тринадцатой) степени из 507788 равен 2.7472529520567

Корень 14 степени из 507788.

Корень 14 (четырнадцатой) степени из 507788 равен 2.5559287626087

Корень 15 степени из 507788.

Корень 15 (пятнадцатой) степени из 507788 равен 2.4009262997208

Степени числа 507788.

507788 в 3 степени.

507788 в 3 степени равно 130932451781127872.

507788 в 4 степени.

507788 в 4 степени равно 6.6485927825035E+22.

507788 в 5 степени.

507788 в 5 степени равно 3.3760756318419E+28.

507788 в 6 степени.

507788 в 6 степени равно 1.7143306929417E+34.

507788 в 7 степени.

507788 в 7 степени равно 8.705165539075E+39.

507788 в 8 степени.

507788 в 8 степени равно 4.4203785987558E+45.

507788 в 9 степени.

507788 в 9 степени равно 2.244615207905E+51.

507788 в 10 степени.

507788 в 10 степени равно 1.1397886671917E+57.

507788 в 11 степени.

507788 в 11 степени равно 5.7877100773592E+62.

507788 в 12 степени.

507788 в 12 степени равно 2.9389297247621E+68.

507788 в 13 степени.

507788 в 13 степени равно 1.4923532470775E+74.

507788 в 14 степени.

507788 в 14 степени равно 7.5779907062699E+79.

507788 в 15 степени.

507788 в 15 степени равно 3.8480127447554E+85.

Какое число имеет такую же сумму цифр как и число 507788?Математика. Найти сумму цифр числа 507788.

Число 507788 состоит из следующих цифр — 5, 0, 7, 7, 8, 8.

Определить сумму цифр числа 507788 не так уж и сложно.

Сумма цифр шестизначного числа 507788 равна 5 + 0 + 7 + 7 + 8 + 8 = 35.

Числа сумма цифр которых равна 35.

Следующие числа имеют такую же сумму цифр как и число 507788 — 8999, 9899, 9989, 9998, 17999, 18899, 18989, 18998, 19799, 19889, 19898, 19979, 19988, 19997, 26999, 27899, 27989, 27998, 28799, 28889.

Четырехзначные числа сумма цифр которых равна 35 — 8999, 9899, 9989, 9998.

Пятизначные числа сумма цифр которых равна 35 — 17999, 18899, 18989, 18998, 19799, 19889, 19898, 19979, 19988, 19997.

Шестизначные числа сумма цифр которых равна 35 — 107999, 108899, 108989, 108998, 109799, 109889, 109898, 109979, 109988, 109997.

Квадрат суммы цифр числа 507788.

Квадрат суммы цифр шестизначного числа 507788 равен 5 + 0 + 7 + 7 + 8 + 8 = 35² = 1225.

Сумма квадратов цифр шестизначного числа 507788.

Сумма квадратов цифр числа 507788 равна 5² + 0² + 7² + 7² + 8² + 8² = 25 + 0 + 49 + 49 + 64 + 64 = 251.

Сумма четных цифр числа 507788.

Сумма четных цифр шестизначного числа 507788 равна 8 + 8 = 16.

Квадрат суммы четных цифр шестизначного числа 507788.

Квадрат суммы четных цифр числа 507788 равна 8 + 8 = 16² = 256.

Сумма квадратов четных цифр шестизначного числа 507788.

Сумма квадратов четных цифр числа 507788 равна 8² + 8² = 64 + 64 = 128.

Сумма нечетных цифр числа 507788.

Сумма нечетных цифр шестизначного числа 507788 равна 5 + 7 + 7 = 19.

Квадрат суммы нечетных цифр шестизначного числа 507788.

Квадрат суммы нечетных цифр числа 507788 равна 5 + 7 + 7 = 19² = 361.

Сумма квадратов нечетных цифр шестизначного числа 507788.

Сумма квадратов нечетных цифр числа 507788 равна 5² + 7² + 7² = 25 + 49 + 49 = 123.

Произведение цифр числа 507788.

Какое число имеет такое же произведение цифр как и число 507788?Математика. Найти произведение цифр числа 507788.

Число 507788 состоит из следующих цифр — 5, 0, 7, 7, 8, 8.

Найти сумму цифр числа 507788 просто.

Решение:

Произведение цифр числа 507788 равно 5 * 0 * 7 * 7 * 8 * 8 = 0.

Числа произведение цифр которых равно 0.

Следующие числа имеют такое же произведение цифр как и число 507788 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.

Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.

Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.

Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.

Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.

Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.

Квадрат произведения цифр числа 507788.

Квадрат произведения цифр шестизначного числа 507788 равен 5 * 0 * 7 * 7 * 8 * 8 = 0² = 0.

Произведение квадратов цифр шестизначного числа 507788.

Произведение квадратов цифр числа 507788 равна 5² * 0² * 7² * 7² * 8² * 8² = 25 * 0 * 49 * 49 * 64 * 64 = 0.

Произведение четных цифр числа 507788.

Произведение четных цифр шестизначного числа 507788 равно 8 * 8 = 64.

Квадрат произведения четных цифр шестизначного числа 507788.

Квадрат произведения четных цифр числа 507788 равен 8 * 8 = 64² = 4096.

Произведение квадратов четных цифр шестизначного числа 507788.

Произведение квадратов четных цифр числа 507788 равно 8² * 8² = 64 * 64 = 4096.

Запишите числа которые в сумме дают число 507788.

Задача: Данно число 507788.Какие 2(два) числа дают в сумме число 507788?Решение:

1) 68095 + 439693 = 507788

2) 251026 + 256762 = 507788

3) 105168 + 402620 = 507788

4) 170719 + 337069 = 507788

5) 68821 + 438967 = 507788

Какие 3(три) числа дают в сумме число 507788?Решение:

1) 148790 + 13865 + 345133 = 507788

2) 15100 + 29919 + 462769 = 507788

3) 54527 + 122010 + 331251 = 507788

4) 145100 + 91256 + 271432 = 507788

5) 67025 + 66930 + 373833 = 507788

Какие 4(четыре) числа дают в сумме число 507788?Решение:

1) 101326 + 114869 + 124641 + 166952 = 507788

2) 101906 + 92128 + 84247 + 229507 = 507788

3) 27784 + 40931 + 178294 + 260779 = 507788

4) 44801 + 41472 + 34982 + 386533 = 507788

5) 108611 + 73632 + 118162 + 207383 = 507788

Какие 5(пять) чисел дают в сумме число 507788?Решение:

1) 20322 + 72446 + 23861 + 91226 + 299933 = 507788

2) 67517 + 23690 + 122284 + 47102 + 247195 = 507788

3) 69369 + 85516 + 27717 + 138613 + 186573 = 507788

4) 101263 + 55115 + 38108 + 48570 + 264732 = 507788

5) 71490 + 38877 + 101453 + 60392 + 235576 = 507788

Источник

Уравнения

В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.

Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант2018)

а) Решите уравнение cos2x = 1-cos(п/2-x)

б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п].

Алгоритм решения:

Пункт а)

При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие тригонометрические уравнения.

Пункт б)

Строим числовую ось.
Наносим на нее корни.
Отмечаем концы отрезка.
Выбираем те значения, которые лежат внутри промежутка.
Записываем ответ.

Решение:

Пункт а)

1. Преобразуем правую часть равенства, используя формулу приведения cos(π/2−x)=sinx. Имеем:

сos2x = 1 – sin x.

Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:

cos(2х)=1−2sin² х

Получаем такое уравнение: 1−sin ²x=1− sinx

Теперь в уравнении присутствует только одна тригонометрическая функция sinx.

2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:

1−2t²=1−t,

−2t²+t=0,

t (−2t+1)=0,

t = 0 или -2t + 1 = 0,

t₁= 0 t₂= 1/2.

3. Делаем обратную замену:

sin x = 0 или sin x = ½

Решаем эти уравнения:

sin x =0↔x=πn, nЄZ

sin(x)=1/2↔x= (-1)ⁿ∙(π/6)+ πn, nЄZ.

Следовательно, получаем два семейства решений.

Пункт б):

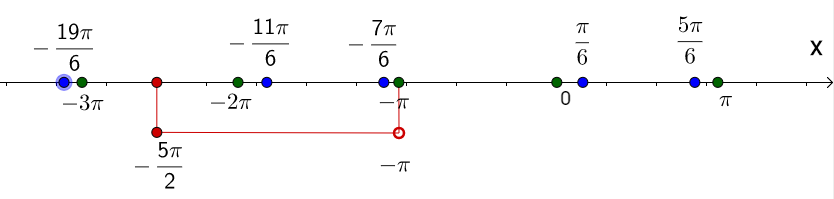
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.

2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).

3. Красным цветом помечаем концы промежутка.

4. В указанном промежутке расположены три корня что три корня: −2π;−11π/6 и −7π/6.

Ответ:

а) πn, nЄZ; (-1)ⁿ∙(π/6)+ πn, nЄZ

б) −2π;−11π6;−7π6

Второй вариант задания (из Ященко, №1)

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

Алгоритм решения:

Пункт а)

Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.

Пункт б)

Строим координатную плоскость и окружность единичного радиуса на ней.
Отмечаем точки, являющиеся концами отрезка.
Выбираем те значения, которые лежат внутри отрезка.
Записываем ответ.

Решение:

Пункт а)

1. Вводим замену t = 4^{cos х}. тогда уравнение примет вид:

Решаем квадратное уравнение с помощью формул дискриминанта и корней:

D=b² – c = 81 – 4∙4∙2 =49,

t₁= (9 – 7)/8= ¼, t₂ = (9+7)/8=2.

3. Возвращаемся к переменной х:

Пункт б)

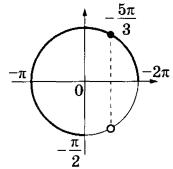
1. Строим координатную плоскость и окружность единичного радиуса на ней.

2. Отмечаем точки, являющиеся концами отрезка.

3. Выбираем те значения, которые лежат внутри отрезка..

Это корни . Их два.

Ответ:

а)

б)

Третий вариант задания (из Ященко, № 6)

а) Решите уравнение .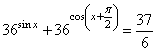

б) Найдите все корни этого уравнения, принадлежащие отрезку .

Алгоритм решения:

Пункт а)

При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.

Пункт б)

Решаем неравенства для каждого случая.
Записываем ответ.

Решение:

а)

1. По формулам приведения .

2. Тогда данное уравнение примет вид:

3. Вводим замену . Получаем:

Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней:

Оба корня положительны.

3. Возвращаемся к переменной х:

Получили четыре семейства корней. Их бесконечно много.

б)

4. С помощью неравенств находим те корни, которые принадлежащие отрезку :

Для корней

Получаем одно значение .

Для корней ни одного значения корней нет.

Для корней есть одно значение ;

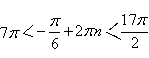
Для корней есть одно значение .

Ответ:

а) ; ;

б) .

Источник

В треугольнике ABC известно, что AC=BC, высота AH=8, BH=20. Найдите tg∠BAC.

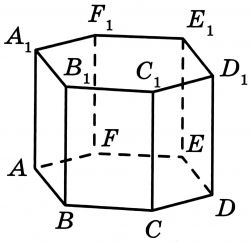
Найдите объём многогранника, вершинами которого являются вершины A₁,B₁,F₁,E правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 10, а боковое ребро равно 9.

В группе туристов 32 человека. Их вертолётом доставляют в труднодоступный район, перевозя по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Г. полетит четвертым рейсом вертолёта.

Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось три броска? Ответ округлите до сотых.

Найдите корень уравнения (left(dfrac19right)^{x+4}=729)

Найдите значение выражения (log_61{,}25cdotlog_{0{,}8}6)

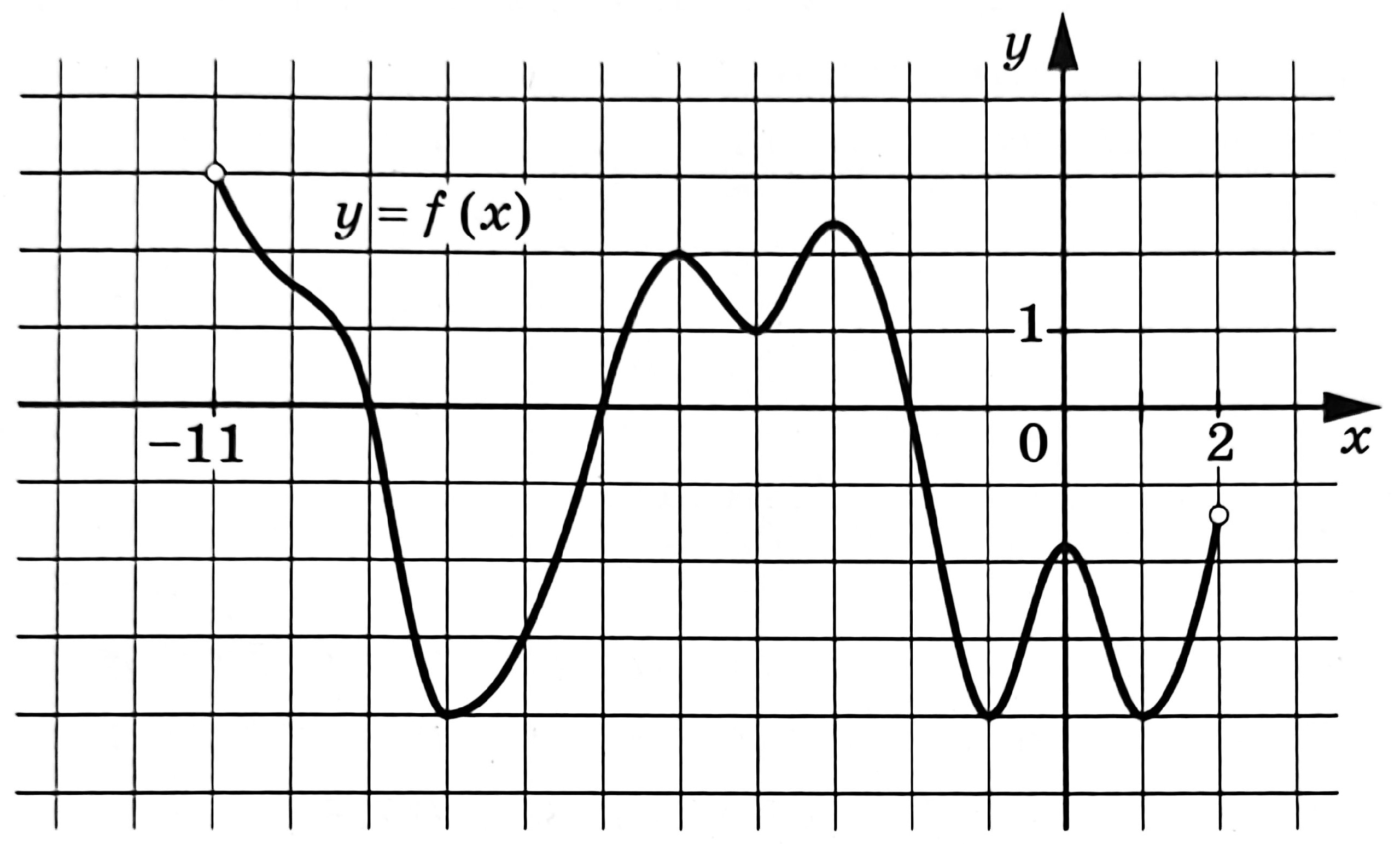
На рисунке изображен график функции y=f(x), определенной на интервале (-11;2). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна или совпадает с прямой y=-4.

Высота над землей подброшенного вверх мяча меняется по закону (h(t)=1+11t-5t^2), где (h) – высота в метрах, (t) – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?

Имеется два сосуда. Первый содержит 25 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 52% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 53% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

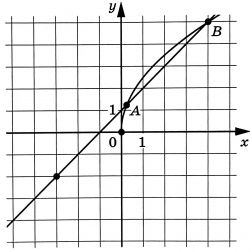
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точках A и B. Найдите абсциссу точки A.

Найдите наименьшее значение функции (y=6x-6sin x+17) на отрезке (left[0;dfrac{pi}{2}right])

а) Решите уравнение (log^2_2(8x^2)-log_4(2x)-1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0{,}4;0{,}8])

Сторона основания правильной четырехугольной пирамиды SABCD относится к боковому ребру как 1:√2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M.
а) Докажите, что сечение пирамиды SABCD плоскостью α – это четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6.

Решите неравенство (dfrac{sqrt{x-2}left(4-3^{x-1}right)}{2^{1-x^2}-3}geqslant0)

15 июня 2025 года Данила Сергеевич планирует взять кредит в банке на 4 года в размере целого числа миллионов рублей. Условия его возврата таковы:
– в январе каждого года действия кредита долг увеличивается на 15% от суммы долга на конец предыдущего года;
– в период с февраля по июнь в каждый из 2026 и 2027 годов необходимо выплатить только начисленные в январе проценты по кредиту;
– в период с февраля по июнь в каждый из 2028 и 2029 годов выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 20 млн рублей. В ответ запишите количество миллионов.

Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F. Точка D – основание высоты, опущенной на AB. I и J – центры окружностей, вписанных в треугольники BCD и ACD.
а) Докажите, что E и F лежат на прямой IJ.
б) Найдите расстояние от точки C до прямой IJ, если AC=2√3, BC=2.

Найдите все значения (a), при каждом из которых оба уравнения (a+dfrac{x}3=|x|) и (2a+x=sqrt{2a^2+4ax-x^2+12}) имеют ровно по 2 различных корня, и строго между корнями каждого из уравнений лежит корень другого уравнения.

Трёхзначное число, меньшее 700, поделили на сумму его цифр и получили натуральное число n.
а) Может ли n равняться 64?
б) Может ли n равняться 78?
в) Какое наибольшее значение может принимать n, если все цифры ненулевые?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Источник

Целое вещественное
шестизначное
четное
число 507788
является составным.

35 — сумма цифр.
24 — количество делителей у числа.
Сумма делителей: 944832.
507788 и 0.0000019693257816254027 — обратные числа.

Число 507788 представляется произведением: 2 * 2 * 37 * 47 * 73.

Перевод числа 507788 в другие системы счисления:
двоичная система: 1111011111110001100, троичная: 221210112222, восьмеричная: 1737614, шестнадцатеричная: 7BF8C.
Конвертация из числа байтов это 495 килобайтов 908 байтов .

Азбука Морзе для числа: ….. —— —… —… —.. —..

Число 507788 — не число Фибоначчи.

Синус числа 507788: -0.1859, косинус числа 507788: 0.9826, тангенс числа 507788: -0.1892.
Число 507788 имеет натуральный логарифм: 13.1378.
Десятичный логарифм числа 507788: 5.7057.
712.5925 — квадратный корень из числа, 79.7800 — кубический.
Возведение в квадрат: 2.5785e+11.

Число секунд 507788 это 5 дней 21 час 3 минуты 8 секунд .
Цифра 8 — это нумерологическое значение этого числа.

Источник